一种圆弧过渡阶梯型超声变幅杆的节点法兰优化与参数型设计*

路 崧，周成全，冯广智，刘家郡，李明雨，刘正锋

(1.哈尔滨工业大学 深圳研究生院，广东 深圳 518118；2.大族激光科技产业股份有限公司，广东 深圳 518103；3.吉林大学 机械科学与工程学院，吉林 长春 130012)

0 引 言

在功率超声加工设备中，超声振动系统主要由超声波发生器、换能器、超声变幅杆和工具头(有时又叫模具头)组成[1]。超声变幅杆可以把机械振动幅度放大，还可以在换能器和声负载之间进行阻抗匹配。除此之外，变幅杆可以在节点处(即振动为零的法兰处)固定整个振动系统，从而减少非超声组件对超声系统的频率和阻抗干扰。

在功率超声加工中，按照振动类型，变幅杆可以分为纵向振动、弯曲振动、扭转振动变幅杆[2]。纵向振动变幅杆最简单也最常用。纵振变幅杆可分为简单型和复合型，简单型按母线形状来分主要有：指数形、悬链线形、阶梯形和圆锥形。复合变幅杆是根据实际需要由简单型结合而成。变幅杆传统的设计主要采用解析法，从经典理论出发，建立纵振波动方程，根据边界条件确定其解。但对于截面形状比较复杂的变幅杆，不易给出解析解，这时就可以利用有限元分析软件ANYS Workbench，基于有限元理论对变幅杆建模并进行动力学分析，可获得谐振频率、位移节点和放大系数等重要性能参数。

陈俊波、赵波等人[3-4]也对变幅杆节点法兰优化进行了研究，不过他们只是设计了简单的薄板式法兰，强度小，不易保证加工质量，更难以装夹。

本文将借助ANSYS Workbench软件来设计和优化一种节点处法兰强度高、易于装夹、结构美观的圆弧过渡阶梯型变幅杆。

1 变幅杆初步设计

本文设计一种用于塑料焊接的、纵振带有过渡圆弧的阶梯型变幅杆。

本研究选用20 000 Hz数字稳频超声发生器和20 000 Hz压电超声换能器，并在超声变幅杆小端面连接有20 000 Hz的钛合金超声模具，用超声领域常用的优质材料钛合金TC-4来设计超声变幅杆。与变幅杆连接的换能器端面直径和模具端面直径分别是38 mm和80 mm，已知变幅杆与换能器连接处，变幅杆直径要大于换能器直径；变幅杆与超声模具连接处，变幅杆直径要小于超声波模具直径，这样才能起到能量集中、振幅增大的目标。本研究选用钛合金TC-4作为变幅杆材料，变幅杆大径为D=48.5 mm，变幅杆小径d=35 mm。

钛合金模具约3.5 kg，超声换能器约1.5 kg。钛合金TC-4性能参数：密度ρ=4 440 kg/m3，声速C1=5 300 m/s，弹性模量110 GPa。钛合金变幅杆的设计频率f0为20 000 H。

设变幅杆粗端直径D与长度L的比值为α，则：

α=D/L

(1)

式中：D—变幅杆大径；L—变幅杆长度。

两端直径比为：

N=D/d

(2)

式中：D—变幅杆大径；L—变幅杆长度。

变幅杆共振频率理想值f0为：

f0=C1/2L

(3)

式中：C1—钛合金棒中声速；L—变幅杆长度。

频率降低系数为：

β=f1/f0

(4)

式中：f1—变幅杆的实际共振频率；f0—变幅杆共振频率理想值。

为了减少阶梯型变幅杆在截面突变处应力集中，常常在此处添加圆弧过渡，过渡圆弧半径对变幅杆共振频率有较大影响，对应某一确定N和α值的变幅杆，存在一个最佳过渡圆弧半径Rop，使该变幅杆的共振频率与按照无限长细棒中声速计算的共振频率f0一致。设定完成以上参数后，则变幅杆的初步设计过程如下[5]：

(1)计算变幅杆近似长度L1；

(2)根据D和L1确定α值；

(3)根据D和d确定N值；

(4)根据N和α由两者的关系曲线找到对应的β值；

(5)计算出了变幅杆的长度L；

(6)根据最佳半径Rop和N的关系曲线，找到对应的Rop/d值，则由d求得Rop。

由于确定β时所适应的为近似长度L1，β也是近似值，但是误差值不超过1%，而且变幅杆裸杆添加节点法兰后会有一定的频率偏移和节点偏移，在节点法兰确定后，最终变幅杆的实际长度以ANSYS有限元方法参数型设计确定。

2 节点优化(节点法兰设计)

由于需要在变幅杆节点处添加法兰设计，用于固定超声组件，或者用于隔离恶劣的工作环境对超声波换能器的污染，常见的方法是在变幅杆节点处延伸出一定厚度的薄板，此处笔者根据经验，取厚度为2 mm，结合上文的尺寸设计，现在变幅杆的示意图如图1所示。

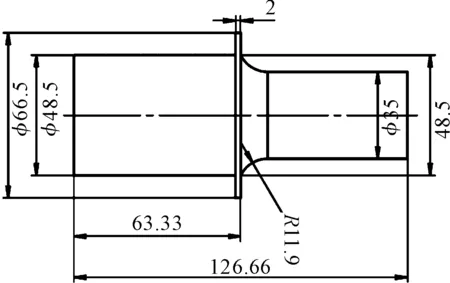
图1 拥有薄板式节点法兰的变幅杆(单位：mm)

然而该种法兰厚度过薄，当需要轴向与径向都完全固定时，若夹持位置离轴心较远，则法兰挠曲变形较大，超声末端有负载时，法兰处无法保证足够的刚度；若夹持位置较轴心较近，则固定方式会较大的影响共振频率。另外，法兰厚度过薄，不容易保证法兰的加工质量，会降低超声组件与夹持装置的同轴度。

本文考虑在该种薄法兰的外侧加块，结构如图2所示。

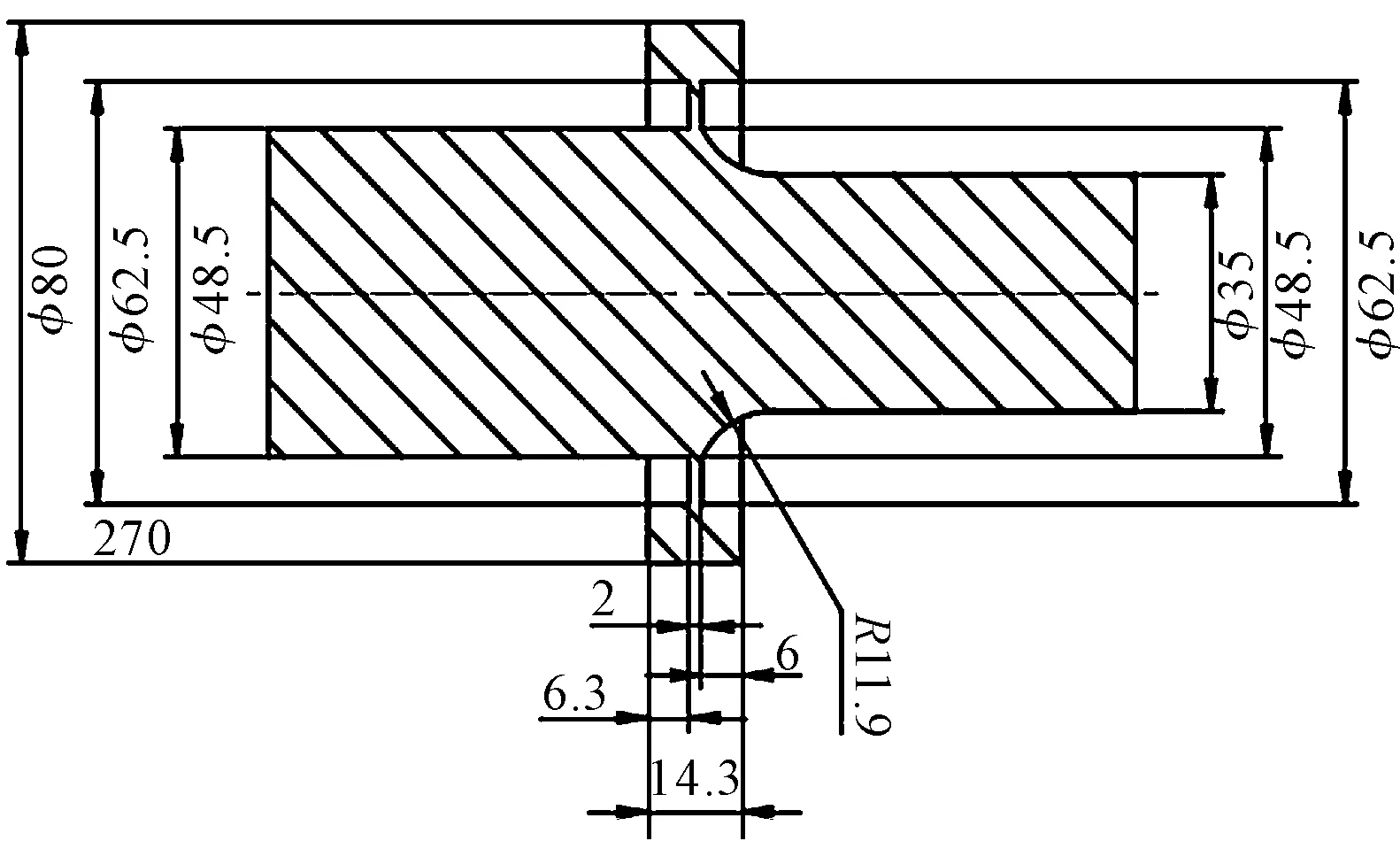
图2 拥有块状节点法兰的变幅杆(单位：mm)

本研究再通过ANSYS的形状优化模块对该添加块进行优化，实现在质量增加较少的情况下，保持或者增强法兰与变幅杆主体连接处的强度。ANSYS Workbench提供了形状优化系统。在形状优化过程中[6]，ANSYS给每一个单元分配一个伪密度，伪密度介于0和1之间，0代表单元可以切除，1代表单元保留，在服从体积降低比例的约束下，通过变化单元的伪密度使结构刚度达到最大化，计算结束后，给出伪密度的等值线图，从而得到形状布置的依据。

为了排除变幅杆主体对结构刚度的影响，本研究把法兰部分单独分割出来做形状优化。过程[7]如下:

(1)创建形状优化模块，修改单位，导入SW创建的模型；

(2)设置材料参数，划分网格，粗略设计选用自动网格划分法；

(3)设置边界条件和载荷，对块状下表面和外表面添加固定约束，对模型整体添加重力加速度，对环形内表面添加超声组件其余部分的总重力，约为58.8 N，注意与重力加速度方向一致；

(4)设置体积优化比例，初步设置为40%；

运行程序，得到的结果如图3所示。

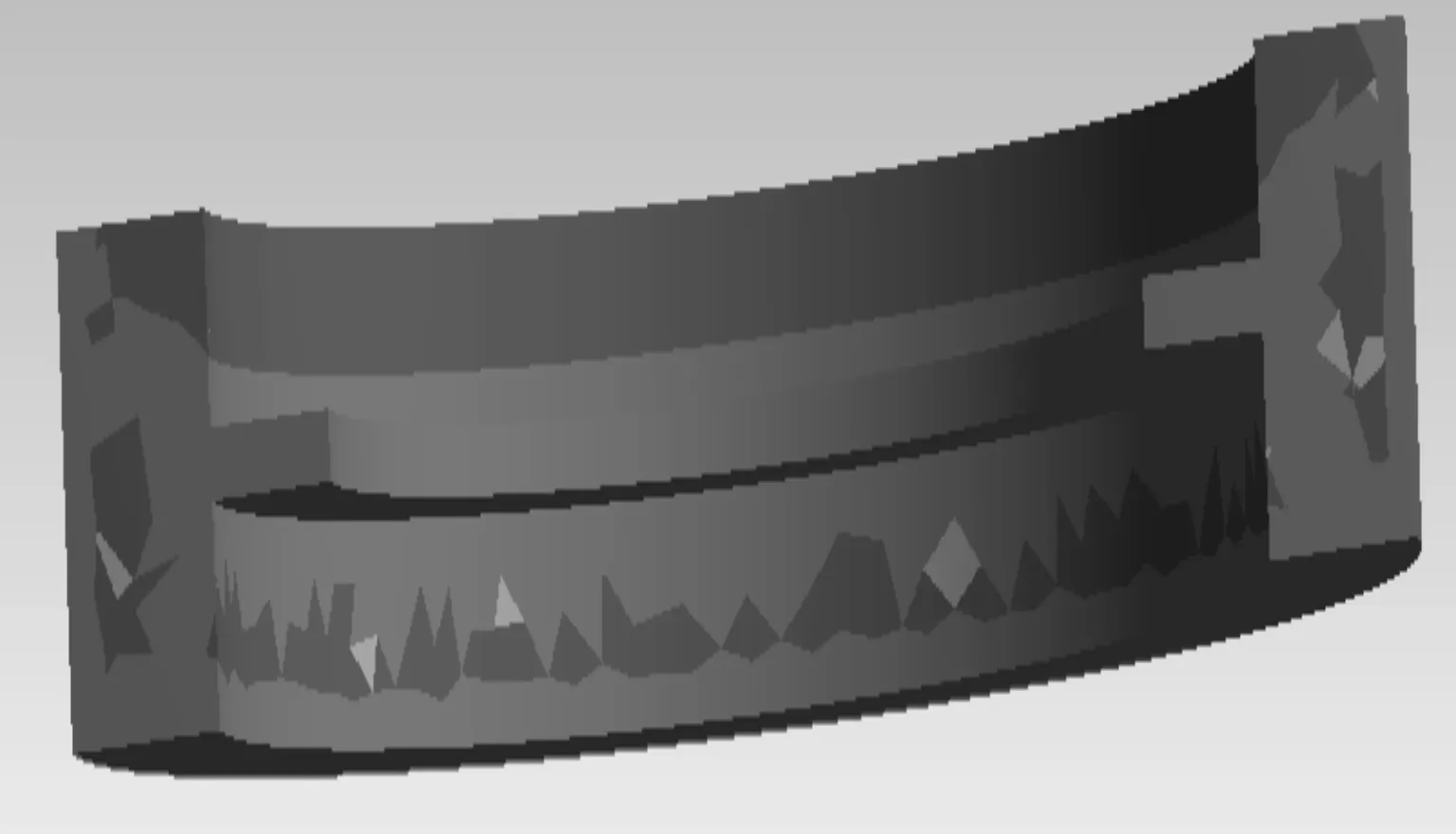
图3 ANSYS形状优化的结果(剖视图)

(5)根据上一条的结果优化法兰部分的形状，进行法兰形状优化；

优化之后，变幅杆形状和尺寸如图4所示。

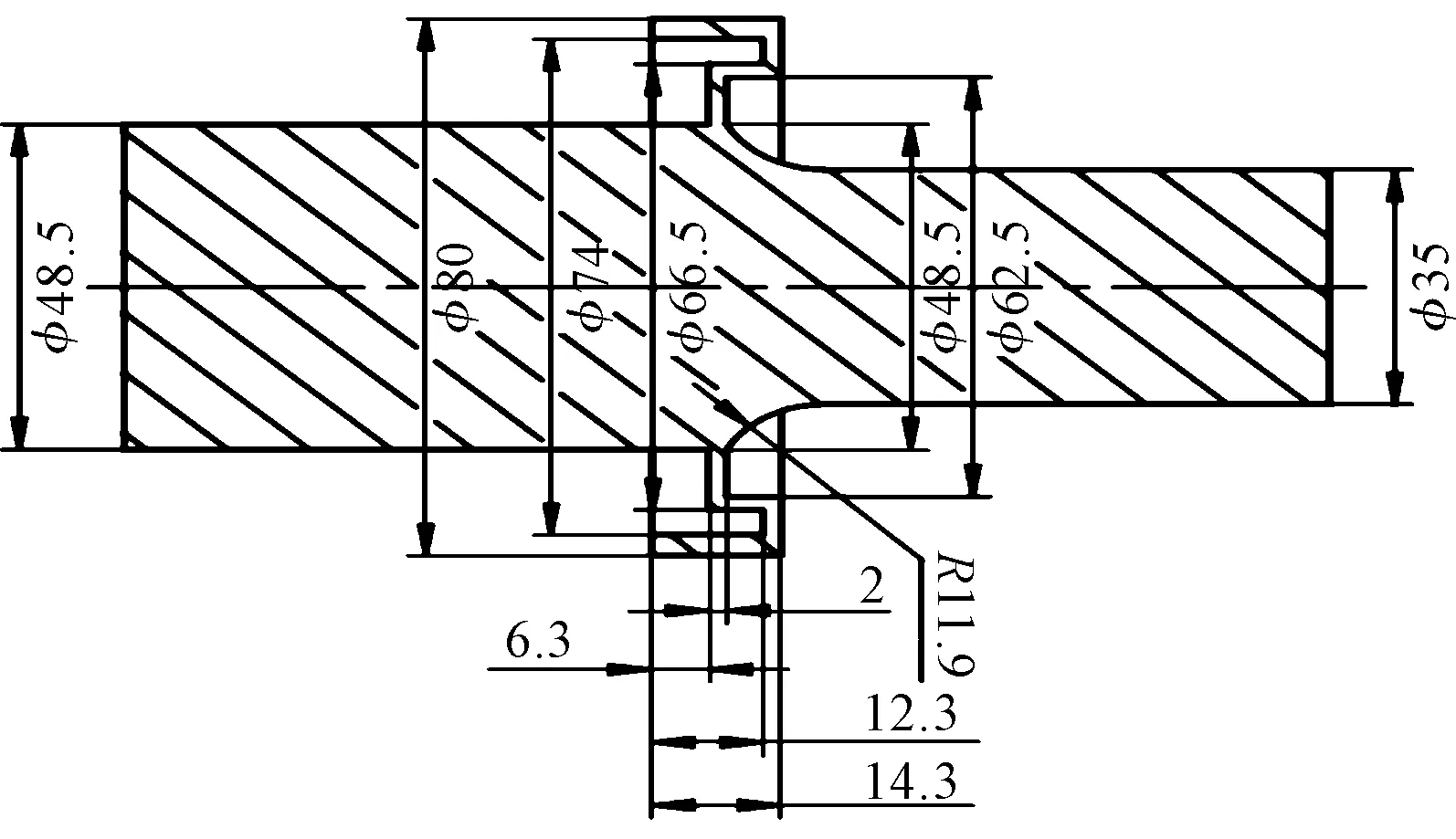
图4 优化后的变幅杆形状尺寸(单位：mm)

(6)对上述模型进行ANSYS静力分析，得到结果，与薄片式节点法兰变幅杆的静力分析结果进行比较。

对比优化前后的变幅杆静力分析结果如表(1,2)所示。

表1 静力分析结果—优化后的变幅杆

表2 静力分析结果-拥有薄板式节点法兰的变幅杆

由表可知：薄片状法兰式变幅杆相比优化后的变幅杆，质量增长7.5%，等效应力减少21.4%，最大主应力减少59.6%，所以该形状优化方案可行。另外，笔者进一步对优化后的法兰部分提高体积优化比例和添加倒角，进一步降低质量，降低加工难度和提高结构强度。

3 变幅杆参数型优化

由于对裸杆变幅杆添加法兰，会不同程度使变幅杆的实际共振频率偏离理想频率，而且还会造成节点偏移，造成振动无法有效传递，对于非常规的变幅杆现在一般都要借助于ANSYS有限元工具进行模态分析，验证其符合理想的超声传递结构，另外可以通过ANSYS DesignXplorer工具对变幅杆进行参数型设计。

所谓参数型设计，就是把结构的某些参数(纵振变幅杆设计中一般是长度)设置成设计变量，对设计变量设置变化区间，在变化区间内对设计变量进行取值和组合得到不同的设计变量组，对各变量组对应的结构和条件进行运算，得到对应结果，分析设计变量组及其对应结果，就能得到各设计变量之间或者设计变量与结果的关系，并且能设置结果目标进行目标驱动优化设计。

本文就是将变幅杆的两圆柱长度设置为设计变量，设置其可变范围，进行目标驱动优化，得到法兰处变形最小，共振频率为19 750 Hz～20 100 Hz区间内(该区间为所选用的数字超声波发生器自动追频范围，该范围内超声组件可稳定工作)，且振型轴向均匀分布的变幅杆长度参数。

当设计参数在10个左右或者更多时，一般选用响应曲面法(response surface optimization)，或者是先进行参数关联分析(parameters correlation),确定参数间的关联性，去除不必要的参数。而本文至此只有两个圆柱长度没有确定，所以采用直接优化法。具体步骤是：

(1)创建模态分析模块和谐响应分析模块，设置材料，钛合金TC-4；

(2)参数化建模，添加固定孔和通风孔，设置两长度为设计变量，初始值均为63.33 mm；

(3)划分网格，进行模态分析[8]；

(4)设置载荷和约束条件，进行谐响应分析，采用模态叠加法，阻尼参数为0.005，同时设置法兰内部下表面变形和变幅杆末端最大变形谐响应频率，结果如图5所示；

(5)添加DOE模块[8]，手动设置长度区间53 mm<63.33 mm<73 mm连续取值，采用CCD算法(Central Composite Design)，优化目标是法兰内部下表面变形为0和变幅杆末端最大变形谐响应频率位于19 750 Hz～20 100 Hz区间；

(6)运行计算，得到候选点，从中选出两长度较接近的组合，代入模型，得到变幅杆两圆柱长度均为66.25 mm，谐振频率19 797 Hz，两端变形比69.298/38.996=1.92，变比较大，满足纵振位移放大条件。

谐响应分析位移-优化后的变幅杆如图5所示。

图5 谐响应分析位移-优化后的变幅杆(mm)

保证加工精度，将加工完成的变幅杆连接20 000 Hz的超声压电换能器和设计加工完成的20 000 Hz超声模具，再给换能器连接20 000 Hz、2 000 W的数字追频超声波发生器，整个超声系统能够连续稳定的纵振工作，无异常尖啸，且法兰处振幅为0，表明整个设计方案过程良好。

法兰振幅测量结果如图6所示。

图6 测量超声系统频率和法兰振幅

4 结束语

根据变幅杆经典设计理论和ANSYS有限元软件，本文设计了一种圆弧过渡的阶梯型纵振变幅杆，并且在变幅杆节点处优化设计了一种便于装夹、结构轻便美观、易于加工的法兰结构；用ANSYS的参数型设计工具，优化变幅杆的长度，校正节点位置恰好落于法兰处；最后将超声发生器、超声变幅杆和超声换能器组装运行，调节振幅。

超声系统可稳定工作在19.75 kHz～20.15 kHz的超声发生器追频范围内，综合工作频率20.09 kHz，表明整个设计方案良好；用超声振幅测量仪测量得到变幅杆法兰处振幅为0 μm，表明变幅杆法兰处基本无振动，没有过多的能量损失，没有漏波，适合装夹。