基于湍流分散的磨粒流场分析及加工实验研究*

2019-01-02陈俊超陈国达傅昱斐

机电工程 2018年12期

张利，陈俊超，陈国达，傅昱斐

(浙江工业大学机械工程学院，浙江杭州 310032)

0 引言

钛合金人工关节是一种植入人体的医疗器械，预期使用寿命为10～20年，甚至更长[1]。人们对它的表面质量要求很高。然而钛合金材料具有导热系数低、塑性弱、硬度高、弹性模量低等特点，导致切削加工性能差[2-3]，人工关节表面结构又普遍比较复杂，所以传统的机械加工方法很难达到理想的效果。

针对这种表面质量需求较高，但构造却比较复杂的钛合金工件，学者们提出了许多新型的加工方法，比如振动抛光[4]、电化学抛光[5]、磁性研磨抛光[6]等。这些加工方法各有优缺点：比如振动抛光方法所需的装置简单，适用性强，但抛光质量相对较低，且容易产生二次损伤；电化学抛光为非接触式抛光，它能有效避免工件表面产生残余应力及二次损伤，但该方法难以保证工件表面材料去除的均匀性，整体抛光效果较差；磁性研磨抛光根据介质不同可以细分为磁性磨料研磨和磁性流体研磨，实际抛光中磁性流体研磨效果相对更好，但它主要适宜加工一些凸形零件的表面，加工范围存在局限性。

针对复杂结构化表面的超精密加工，计时鸣等[7]提出了一种软性磨粒流加工方法。该方法首先仿照复杂表面的几何结构设计相对应的仿形约束流道，再用弱粘性的流体与磨粒混合制备软性磨粒流，最后把软性磨粒流循环通入仿形约束流道，对待加工表面进行加工[8]。该方法较其他加工方法普适性强，针对不同的表面结构易于调整加工参数，加工效果良好，适合加工各类复杂的钛合金表面。

软性磨粒流是一种固-液两相流，在两相流领域，对于固相和液相的耦合方式有两种比较典型的描述，分别是欧拉-欧拉描述和欧拉-拉格朗日描述[9]。两种描述的区别主要在于对固相的描述不同。软性磨粒流的颗粒浓度一般较低，可以忽略固相对液相的影响，所以一般采用欧拉-拉格朗日法对其进行数学建模。

在对仿真过程中的湍流运动进行描述时，雷诺时均法是一种比较常见的建模方法[10]。该方法的优点是计算量小，得到的结果已经能够满足大多数实际工程的需要；缺点是对湍流物理量进行时间平均后抹平了所有的脉动值，无法体现湍流特有的无序脉动这一特点。比如李琼等[11]在模拟液压油箱中固体颗粒的运动和李绍武等[12]在模拟粉尘运动时，都采用了基于雷诺时均法的湍流模型，他们模拟得出的颗粒运动轨迹虽然无序，但轨迹本身并不会随时间而改变；从观测颗粒运动的角度出发，这不是希望得到的结果。

因此，为了尽可能真实地模拟颗粒的运动，本文提出一种湍流分散方法，在雷诺时均法的基础上还原湍流的速度脉动特征，然后在此基础上进行流场分析，最后进行加工实验进行验证。

1 流场数学模型

1.1 基于欧拉法的液相湍流方程

湍流方程由两部分组成：第一部分为运用雷诺时间平均思想在经典Navier-Stokes方程(以下简称N-S方程)基础上[13-14]推导出的湍流基本方程，即雷诺时均方程；第二部分是应用最广泛的标准k-ε湍流双方程，该方程是为了使雷诺时均方程封闭而选用的湍流补充方程。

湍流区别于层流的关键在于湍流内部存在尺度不一的涡旋运动，这些涡旋运动一般被认为仍然符合N-S方程的描述[15]。在不考虑温度变化的情况下，理论上对湍流的每一个瞬时状态用N-S方程中的连续性方程和动量方程就可以准确地描述湍流运动，但这种直接数值模拟方法涉及的计算量很大[16]，不能满足实际工程的需要。

因此，本文依据雷诺时间平均思想在N-S方程基础上构建雷诺时均方程(RANS方程)。

连续性方程如下：

(1)

动量方程(以x方向为例)如下：

(2)

(3)

(4)

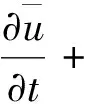
(5)

用同样的方法可推导出湍流在y、z方向上的动量方程，然后结合湍流连续性方程，整理得出RANS方程如下：

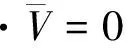
(6)

(7)

式中：ρ—流体密度；▽—梯度算子；V—速度矢量；u，v，w—速度分量；p—压强；μ—流体粘性系数；fx，fy，fz—作用在单位质量上的体积力分量。另外，各个变量上方的横线表示该变量是运用雷诺时均法后得到的时均值。

(8)

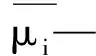
针对新增的k与μt两项，本文选用LAUNDER和SPALDING[18]提出的标准k-ε模型(Standardk-εModel)建立其内在联系：

(9)

(10)

其中，方程中各模型常数一般取值为：

C1ε=1.44，C2ε=1.92，Cμ=0.09，σk=1，σε=1.3。

1.2 基于拉格朗日法的颗粒运动模型

根据牛顿第二运动定律可以得出单颗颗粒的运动方程：

(11)

式中：mp—颗粒质量；Vp—颗粒速度；t—时间；∑Fi—作用在颗粒上的各种力之和。

颗粒在流体中运动时会受到很多力的作用，其中曳力是在任何情况下都不可以忽略的力。本文只考虑颗粒受到曳力的情形。

曳力的大小与流体密度ρ、迎流面积Sp、速度差(v-vp)有关。参考空气阻力的经验公式有:

(12)

可以得到曳力计算公式：

(13)

假设颗粒为球形并考虑曳力的作用方向，上式变为：

(14)

式中：ρ—密度；v—速度；μ—流体粘度；r—颗粒半径。下标p—该物理量为颗粒物理量；未标下标p—除了某些无歧义的物理量外皆为流体物理量；Cd—曳力系数，其值由颗粒雷诺数Rep决定:

(15)

(16)

从曳力的计算公式中可以看出，流体速度是影响曳力大小的主要因素。前文的雷诺时均法抹平了湍流中所有尺度的脉动情况，只体现了所有物理量的平均结果。从研究颗粒运动的角度来说，这种情况体现不出湍流对于颗粒的无序驱动作用。因此，本文在模拟颗粒运动时，拟在一定程度上还原湍流运动特有的无序状态，即湍流分散方法。

在标准k-ε湍流模型中湍流动能k的表达式为：

(17)

(18)

（3）依据前期设计要求，在确定爆破孔及预裂孔位置无误后，可进行钻孔设备合理选择。为保证钻孔精度，本次工程选择110B型潜孔钻机作为预钻机，其具有钻孔基面小、精度高、操作便捷等优点；而在缓冲孔、主爆破孔钻孔设备选择时，则主要采用CM353型钻机。结合角度尺的应用，可以保证缓冲孔坡度的有效控制。

(19)

记速度脉动矢量为U′，那么有：

(20)

式中：I—随机单位向量，用于表示速度脉动的方向。

对于上式中由3个随机参数λ1，λ2，λ3组成的系数，采用一个新的随机参数λ代替，即：

(21)

上式的关键是随机参数λ的取值，理论上来说λ的取值有无限的可能，但实际应用中却不能在无限范围内对λ取值，具体的取值需要结合所模拟的流动情况而定。本文中λ的取值是一个均值为0、标准差为1的随机分布。

因此，曳力的计算公式中流体的速度用重新构建的湍流仿真速度U代替，即：

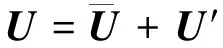
(22)

2 数值模拟

2.1 模型及参数设定

实际加工中的仿型约束流道如图1所示。

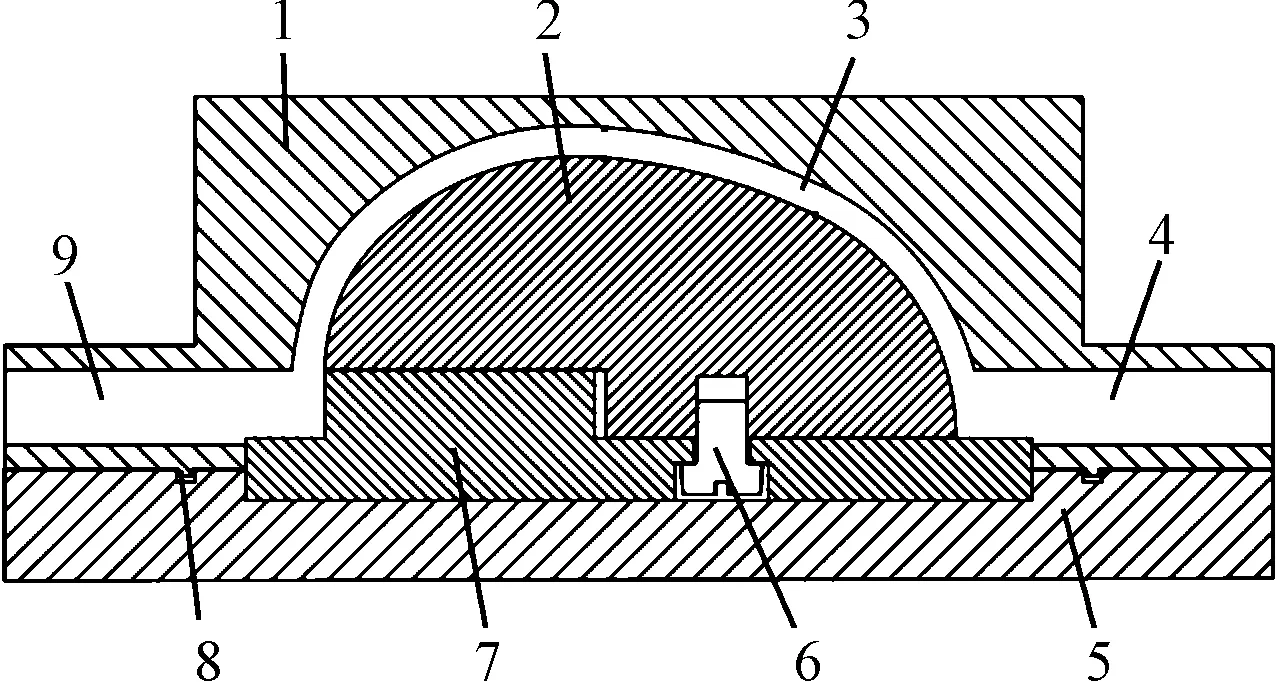
图1 仿型约束流道示意图1-盖板；2-人工膝关节；3-流道；4-流道出口；5-底板；6-螺钉7-固定件；8-密封胶填充槽；9流道入口

图1中，盖板1、底板5以及固定件7作为仿型约束配件，三者组成仿型约束流道，人工膝关节三维模型与仿真流道模型，如图2所示。

图2 物理模型和流道网格划分1-仿型面A；2-仿型面B；3-过度面

人工膝关节模型是参考实际膝关节结构而设计，其中1和2分别是包含6个曲率参数的仿型面，3是仿型面之间的过度面；仿真流道模型是根据图1的仿型约束流道设计，用COMSOL软件对其进行自动网格划分，网格形状为正四面体。

为了便于观测磨粒流流道内的流场分布情况，本研究对图2(b)所示的流道模型进行截面分割，得到的结果如图3所示。

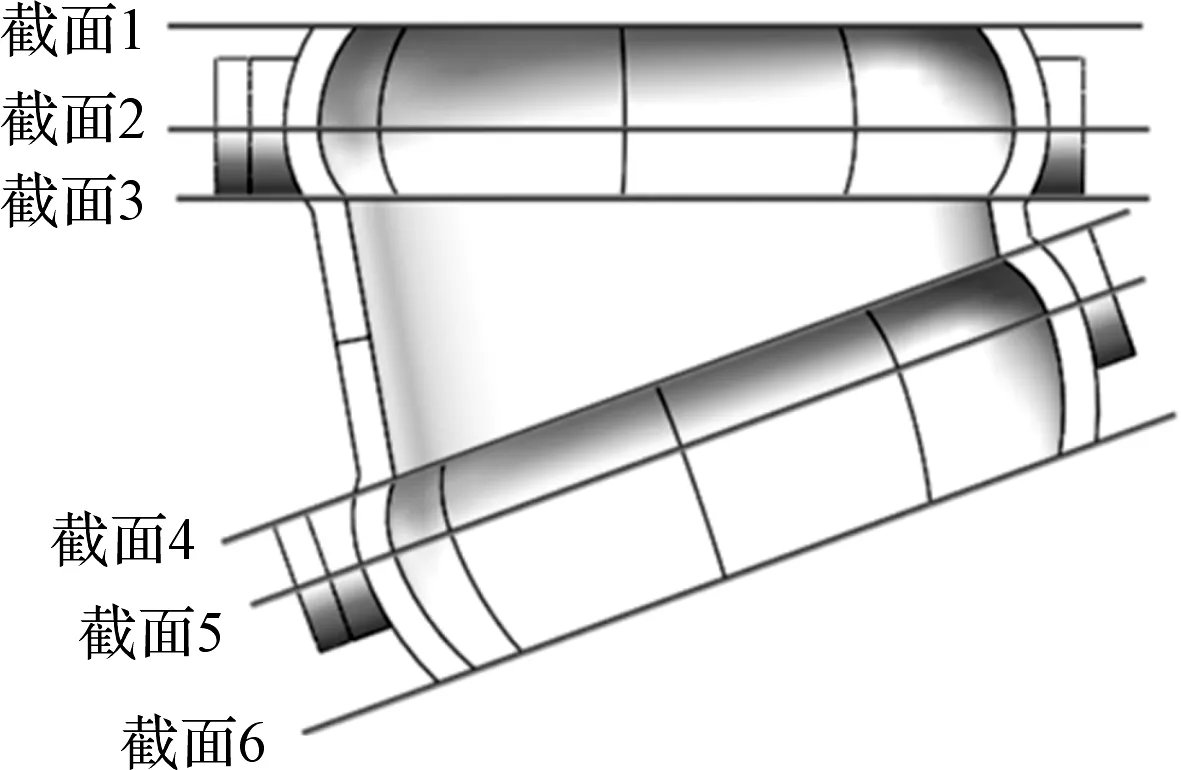
图3 截面示意图

仿真中的一些关键参数如表1所示。

表1 关键仿真参数

2.2 仿真结果

0.1 s时刻流道截面速度分布如图4所示。

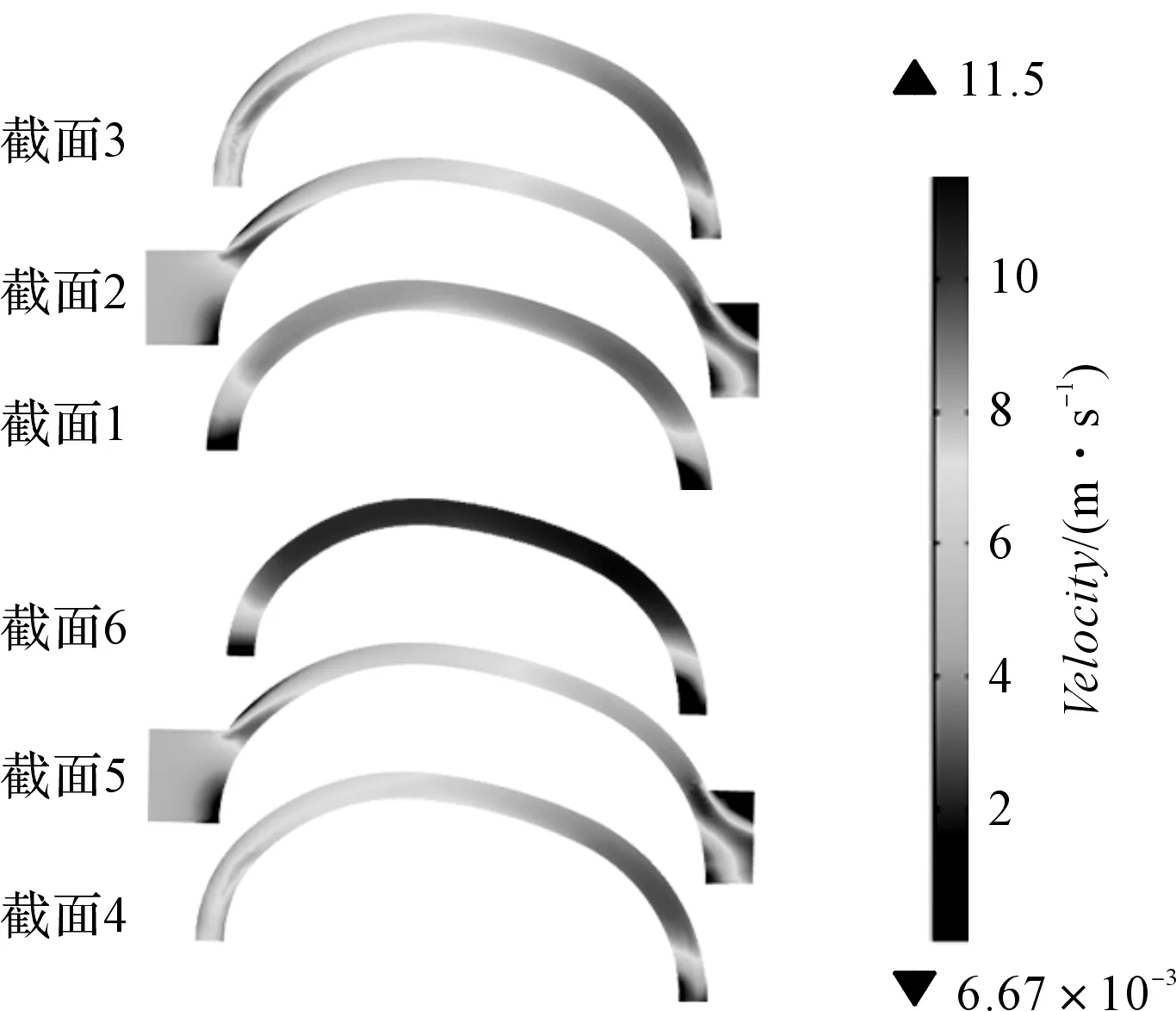
图4 截面速度分布

从整体来看，流道中间部分的速度基本高于初始速度5 m/s，靠近出口部分的速度高于靠近入口部分的速度。从单个仿型面来看，仿型面A的截面1、截面2、截面3的速度分布依次呈现高-低-高的趋势，结合物理模型分析，从相对位置较低的截面1和截面3到相对位置较高的截面2，途中损失了部分速度，导致速度分布呈现高-低-高这一结果。仿型面B的情况类似。

0.1 s时刻流道截面压力分布如图5所示。

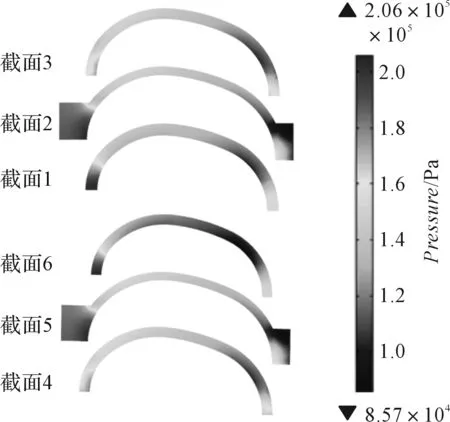
图5 截面压力分布

图5中显示的结果与截面速度分布的结果相反：磨粒流从入口到出口这一过程所受到的压力减小，从截面1到截面6这一过程中，物理位置相对较高的地方压力相对较大。综合上述分析可以得出：磨粒流速度分布和压力分布符合实际加工经验，两者之间存在一定程度的负相关联系，该情况与伯努利方程的内涵相符。

为了直观反映前文提出的湍流分散方法的应用效果，设置如下简单情形：在10 mm的直管一端以5 m/s的速度通入水，在该端部中间以0.001 s的时间间隔释放单颗粒子，粒子在水的曳力作用下运动，分别模拟未应用湍流分散方法时，颗粒的运动过程与运用湍流分散方法时颗粒的运动过程，得到的结果如图6所示。

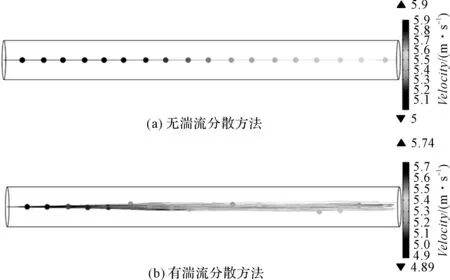
图6 不同模拟方法下颗粒的运动轨迹

从图6(a)中可以看到：在曳力作用下相同位置释放的颗粒都沿着相同的轨迹运动；但图6(b)中相同位置释放的颗粒在曳力作用下的运动轨迹却不相同，轨迹之间也相对无序。两图中颗粒运动轨迹的差别证实了湍流分散方法的有效性。

本研究结合湍流分散方法，对磨粒在人工膝关节加工流道模型内的运动进行模拟仿真，结果如图7所示。

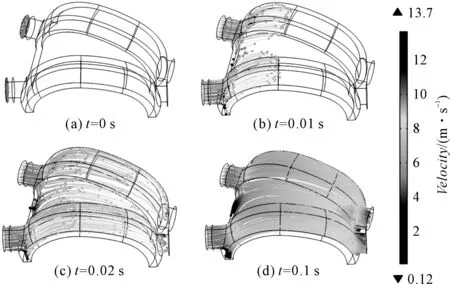
图7 不同时刻的颗粒运动轨迹

从图7中可以看到：t=0时刻磨粒在入口处就绪，流道内并没有磨粒；t=0.01 s时刻有两波磨粒进入了流道，最开始释放的磨粒已经到了流道中部；t=0.02 s时刻已有4波磨粒进入了流道，最初释放的磨粒已到达流道出口；t=0.02 s时刻到t=0.1 s时刻之内磨粒不断进入流道，同时先前进入流道的磨粒也不断从出口离开，磨粒运动的轨迹逐渐增多，直到20波磨粒都进入了流道。图中每条轨迹不同部分的颜色表示粒子运动到该位置时所具有的速度大小。

0.1 s时刻流道内湍流动能分布如图8所示。

图8 0.1 s时刻的湍流动能分布

图8中粒子轨迹的颜色表示0.1 s时刻不同位置的流体所具有的湍流动能，从图中可以看到：绝大部分区域的流体所具有的湍流动能均低于0.4 m2/s2，只有出口部分的湍流动能高于0.4 m2/s2。从湍流动能的分布可以看出几乎整个流道内的流体都已处于湍流状态，但绝大部分区域的湍流脉动程度相对较小。

综合上述分析可以得到：磨粒在进入流道后受到流体曳力的作用而做加速运动，运动过程中与壁面碰撞发生反弹，反弹后的速度方向也因为流体曳力的影响而逐渐变为与流体流动方向一致。但在湍流分散方法的影响下，以相同条件释放的磨粒的仿真运动轨迹不再重合。

考虑到实际加工中造成磨粒无序运动的因素有很多，比如泵的间歇性推动作用、流道入口之前的管路状况等，因此磨粒的仿真运动结果虽然与磨粒的实际运动结果仍存在一定差距，但对于前文所建立的数学模型来说，该仿真结果是符合预期的。

3 加工实验

3.1 平台搭建及参数设定

搭建的实验平台如图9所示。

图9 实验平台示意图1-渣浆泵；2-磨粒回收池；3-加工流道；4-输送管

渣浆泵是整个磨粒流加工过程的动力源，开式磨粒回收池是整个磨粒流加工循环的起点和终点。磨粒流的加工流道，内部安装着表面待加工的人工膝关节实物。两条输送管，其中与泵相连的是加工流道的磨粒流入口管，与磨粒回收池相连的是加工流道的磨粒流出口管。

实验分为粗加工和精加工两个过程，实验参数如表2所示。

表2 加工实验主要参数

实验加工时，磨粒流循环流动加工这一过程会产生大量热能，包括渣浆泵、输送管、磨粒流、加工流道、磨粒回收池在内的所有实验装置和实验材料的温度都会缓慢升高。考虑到离心泵的使用寿命，粗加工和精加工过程都以1 h为加工间隔，到达时间后暂停加工，更换基液，等待0.5 h后继续加工。同时，因为磨粒流中未加分散剂，需要定时搅拌磨粒回收池，防止磨粒沉积。