基于SVM的图像识别在零件分拣系统中的应用*

孙小权，邹丽英

(浙江工业大学 之江学院，浙江 绍兴 312030)

0 引 言

随着自动化技术的发展，在零件生产中的许多人工所做的工作也逐步被自动生产装置所取代，自动上料是零件自动化生产的重要一环。对于小型零件而言，排序上料最常用的装置就是振动盘。振动盘利用零件本身的外观形状、质心分布等特征进行分拣排序，让零件按照设计要求的状态沿轨道送出。而当零件的外观形状、质心分布无法确定零件的送出状态时，振动盘送料就无法实现。

文献[1]通过对图像分割确定零件在传送带上的位置，控制机械手对零件进行了抓取；文献[2]对图像进行了孔洞分析，结合零件的结构特征从而识别不同的零件；文献[3]通过角点检测和模板匹配实现了零件方位识别，识别正确率在90%左右；文献[4]利用PCA与SVM对人脸图片进行识别，取得了较高的识别率。

本研究将针对外观形状、质心分布较均匀的零件在自动化生产中难以实现有方位要求的自动送料问题，对零件的图像采集、图像处理、图像特征提取和分类识别等进行研究和分析，提出以图像识别为核心的零件分拣系统。

1 零件分拣系统方案设计

正畸带环如图1所示。

图1 零件的两个状态

由于生产的需要，该零件在后续加工过程中要求按状态一的方位送到加工位置。该零件可以利用下部的圆弧缺口实现带环中心轴与输送方向垂直，但由于图1零件A上下两边相差一个很小的凹坑，图1零件B上下两边仅是圆弧角度有较小的差异，形状差异很小，质心位置基本居中，振动盘无法将上下两边分出，达不到上料要求。

根据前述的图像识别的思路，本研究在振动盘出料口安装图像识别装置，控制系统根据图像识别的结果，控制推杆将不符合方位要求的零件推出送料轨道，如此图像识别技术与振动盘相结合，就能较好地解决正畸带环上料方位问题。

零件分拣系统如图2所示。

图2 控制系统组成框图

2 图像的小波变换

目前，CCD摄像机拍摄的照片像素较高，数据量较大，须经适当处理，但又要保证图像的主要特征不能丢失。二维小波变换既能降噪，又能在保留主要特征的情况下具有较大压缩比例。

小波变换的原理是通过构造一对正交镜像滤波器[5]，对图像进行滤波处理，得到不同尺度不同方向的高低频分量。对二维图像进行小波变换是分别在水平方向与垂直方向作一维小波变换来实现一层二维小波变换，图像通过一层二维小波变换分解可以得到4个区域：低频区域LL、高频区域HL、LH、HH。其中，低频区域LL表示近似分量，为原图的平滑像，高频区域HL、LH、HH分别表示水平分量、垂直分量和对角分量。对于每次变换得到的低频区域LL可以再次进行小波变换，一幅图像作n次二维小波变换后，低频区域图像的尺寸为原图像尺寸的1/4n。

小波变换分解如图3所示。

图3 小波变换图

图3中，低频区域LL集中了图像的大部分信息，而高频区域则包含了大量的冗余信息和干扰，所以本研究直接对低频区域进行特征提取。由于图像信息相对集中，小波变换不仅能有效地降低维数，去除冗余干扰信息，还能节省空间，提高计算效率。

3 特征提取

识别图片经小波变换，大小已缩小至原图像的1/4n,但是维数仍然太多，不利于后续识别计算，需要进一步进行特征提取，主成分分析法(PCA)是一种常用的基于变量协方差矩阵对信息进行处理、压缩和提取的有效方法，由于其在降维和特征提取方面的有效性，在图像识别领域得到了广泛的应用。PCA算法主要利用K—L变换提取图像的主要成分，构成特征空间，识别时将测试图像投影到此空间，得到一组投影系数，即该测试图像的特征向量[6]。

主成分分析(PCA)具体算法是：(1)将图像的二维矩阵按行转换成一维向量，把一幅大小为M×N的图像的像素矩阵的每行连在一起构造成一个长度D=M×N的特征向量，设有n个训练样本，则构成D×n向量矩阵；(2)求每列均值；(3)计算每列值与均值的差，构建新的D×n向量矩阵；(4)构建协方差矩阵；(5)求协方差矩阵的特征值和特征向量，构造特征图像空间；(6)为了减少维数，可以按照特征值的影响选取影响最大的前q个特征值及其特征向量。由此，原始的M×N维图像经上述转换变成q维。根据这一维数,从主成分系数矩阵和训练样本投影矩阵中取出相应的构成新的主成分系数矩阵和样本投影矩阵。识别时,只需将识别样本向主成分系数矩阵上投影就得到要提取的特征向量[7]。

4 图像识别

根据特征向量进行分类识别的技术较多，如距离分类、聚类分析、神经网络、支持向量机(SVM)等。支持向量机是在统计学习理论基础上发展起来的一种新的机器学习方法，能解决小样本、维数灾难、过学习等问题。支持向量机以构造最优超平面为目标，将不可分的数据映射到高维特征空间中，在高维特征空间中正确区分各类样本。

设有两类线性可分的样本集合：

(1)

它可以被一个最优分类超平面没有错误地分开，并且离超平面最近的向量与超平面的距离是最大的。最优分类面函数为：

(2)

式中:xi—支持向量;ai—拉格朗日系数;b—分类阈值。

对于数据为线性不可分的情况，支持向量机的分类过程则是通过核函数K(xi,yi)定义的非线性变换将输入空间映射到一个线性可分的高维空间，然后在高维空间进行线性分类。其相应的分类函数也变为：

支持向量机最初是针对二分类问题的，当用于多分类问题时，可以以二分类为基础，构造多个二类分类器，求解多个分类器的分类超平面而获得分类问题的最优解[8-9]。

使用训练集建立支持向量机模型需要根据数据特征向量选择合适的核函数和相关参数。径向基函数应用较广泛，可以适应大多数的应用场合。径向基核函数需要设置两个参数，分别是核函数的宽度参数g和误差惩罚系数c。合适的参数可以通过多种方法进行寻优得到，如网格算法、遗传算法、粒子群算法等。

5 实验结果分析

本研究选取图1所示两个零件各一批，一半在向上方位、一半在向下方位采集图片样本，选取不同的样本数作为训练样本，另外样本作为测试样本，借助Matlab程序开发平台和台湾大学林智仁教授等的LIBSVM模式识别与回归的软件包，进行小波变换、PCA降维和分类识别。

(1)小波变换。程序读出图片后，依次进行灰度化、三层小波变换、向量化，保存向量矩阵。零件A的三层小波变换如图4所示。

图4 零件A的三层小波变换

零件B的三层小波变换如图5所示。

图5 零件B的三层小波变换

(2)PCA特征提取。图像经过三层小波变换，成为保留零件主要特征的图片并保存为向量矩阵，向量矩阵经PCA变换，按90%的影响力选取p值，提取适当维数的特征向量。将变换得到的主成分系数矩阵(即变换矩阵)、样本投影矩阵、列向量平均值保存，以供训练和识别使用。选取B零件20个作为训练样本经PCA处理后主成分系数矩阵如表1所示。

训练样本投影矩阵如表2所示。

表2 训练样本投影矩阵20×10

(3)SVM训练与识别。SVM的分类函数和惩罚因子选择是关键，本例根据经验选择径向基函数，核函数的宽度参数g选2，惩罚因子c选1。

训练时，训练样本投影矩阵中每行为一个样本的10维向量，与样本的分类标签作为支持向量机的输入，调用LIBSVM中的svmtrain函数进行训练，训练结果模型保存在文件中，以供识别时调用。

识别测试时，本研究读取待检测样本，进行灰度化、3层小波变换和向量化，通过训练时得到的变换矩阵进行变换，得到检测样本投影矩阵，将前述训练得到的分类模型和检测样本投影矩阵，以及检测样本的分类标签输作为SVM预测模块的输入，即可得到识别率。工程应用时，直接从摄像头获得图片，进行适当裁剪后按上述程序可以得到一个图片的识别结果，从而驱动控制装置的动作。实验结果如表3所示。

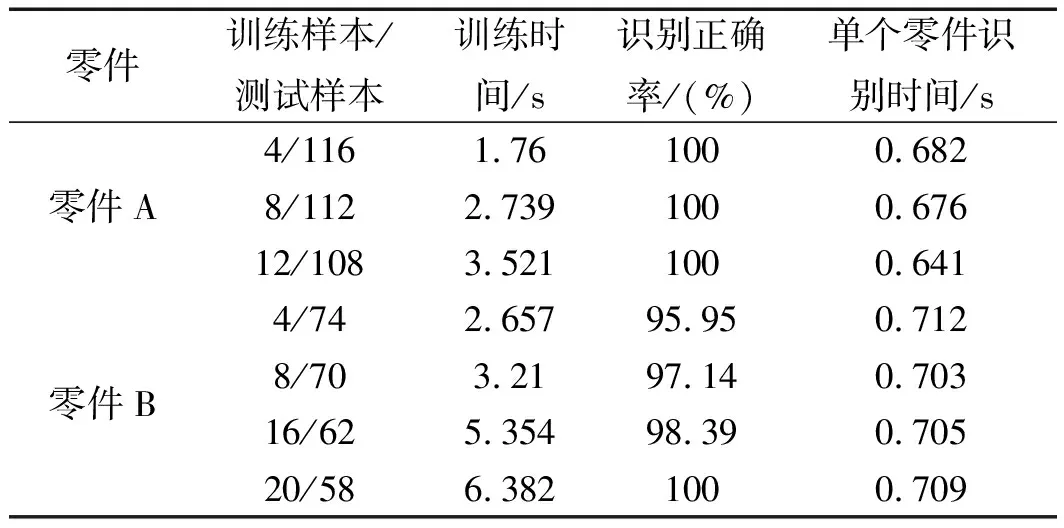
表3 实验结果

6 结束语

本文以正畸带环排位送料为例，通过对零件结构的分析，在振动盘出料口安置CCD采集图像，通过小波变换算法对零件图像进行去噪和降维，使零件图像从40万像素转换成6 000多像素；通过主成分分析法从6 000多像素中提取10维向量作为零件主要特征，10维向量特征作为支持向量机的输入，从而对零件方位进行正确地识别，根据零件的方位状态，控制驱动装置将不合要求的零件推出轨道，为下道工序的生产实现自动送料。

实验结果表明：训练样本达到20以上时，两种零件的识别正确率都达到了100%，单个零件的识别时间在1 s以内，能满足实际生产要求。