基于均匀设计和遗传算法的液动压悬浮抛光工艺参数优化研究*

2019-01-02尹林志朴钟宇李攀星文东辉

机电工程 2018年12期

尹林志，朴钟宇，李攀星，文东辉

(浙江工业大学特种装备制造与先进加工技术教育部重点实验室，浙江杭州 310014)

0 引言

现代科技发展对光学元件、计算机芯片和纳米薄膜衬底的表面质量提出了苛刻要求，需要达到纳米级甚至原子级[1-2]。目前，抛光依然是降低工件表面粗糙度，去除损伤层，得到高精度和高质量表面的主要加工手段[3]。传统的机械抛光和化学机械抛光以磨粒与工件的刚性接触为主，抛光工具容易磨损，难以实现表面的无损伤加工。因此，在传统抛光方法的基础上，出现了许多应用磁学、流体力学、流体流变特性原理得到的柔性悬浮抛光方法，如磁流变抛光(MRF)[4]、浮法抛光(FP)[5]、弹性发射加工(EEM)[6]、动压浮离抛光(HFP)[7]和剪切增稠抛光(STP)[8]。这些抛光方法改变了磨粒与工件的接触方式，有利于抛光加工过程中低表面粗糙度、低损伤表面的形成。其中，MRF作为一种基于计算机控制光学表面成型技术(CCOS)的柔性抛光方法，已成功应用于各类形面超精密加工中，但在加工中必须使用造价昂贵的加工介质(磁流变液)；FP虽然可以获得完好的表面晶格，亚表面没有损伤层，但液动压效应较弱，加工效率低；EEM可获得超光滑无损伤表面，但工件表面易形成波纹，设备要求高；HFP存在动压力分布不均匀、动压浮离盘楔形结构设计难度大的问题；STP利用抛光液的剪切增稠流变特性达到增强把持磨粒的约束力，成功应用于石英晶片、GCr15轴承钢、Si3N4陶瓷的加工中，是一种很有潜力的抛光方法，但长时间抛光会降低抛光液的流变特性。

因此，基于HFP方法，笔者提出了液动压悬浮抛光方法(HSP)[9]，在抛光工具盘的平行区域后面增设约束边界，用约束边界调控平行流场内的压力分布。仿真结果表明：加入约束边界可有效改善工件区域的流体压力均匀性。朱胜伟[10]利用正交试验法研究了加工工况对流场动压力及磨粒与壁面撞击状况的影响，但其只选择了一点作为动压力数据的参考点；谢重[11]利用ABAQUS模拟了加工过程中固相磨粒与工件表面的撞击过程，研究了磨粒速度和角度对撞击后工件表面残余应力沿工件深度方向的分布规律；齐欢[12]通过仿真和实验进一步研究了HSP对工件表面残余应力松弛的影响。

由于抛光工艺参数影响了抛光液的流动特性，而工件区域的流体压力大小和压力均匀性对工件表面的材料去除速率和粗糙度有重要影响，有必要研究抛光工艺参数对流体压力大小和压力均匀性的影响。

本文以ANSYS Fluent软件为计算平台，采用固-液两相流的欧拉模型，对液动压悬浮抛光流场进行CFD数值模拟，研究抛光工艺参数对压力大小和均匀性的影响，同时利用多元非线性回归模型和遗传算法对工艺参数进行优化。

1 液动压悬浮抛光

液动压悬浮抛光工具盘的结构如图1所示。

图1 液动压悬浮抛光工具盘结构示意图D1—抛光工具盘内径；D2—抛光工具盘外径；B—单元结构长度；B0—蓄流槽；B1—楔形区；B2—平行区；B3—约束边界；α—楔形角度；h1—约束高度；h—加工间隙；H—液槽高度

抛光工具盘底部共10个单元，每个单元分为4个区域：蓄流槽、楔形区、平行区和约束边界。

液动压悬浮抛光方法采用抛光液浸没工件的方式，适当粘度的抛光液在楔形抛光工具盘旋转驱动下，快速通过间隙收敛的液楔，形成液动压使抛光工具悬浮，保持了磨粒与工件表面处于非接触状态，使工件在液动压力稳定区完成加工。

2 模型建立

2.1 流体控制方程

液动压悬浮抛光楔形区流体的实际流动为湍流，本文采用连续性方程、N-S方程和基于各向同性涡粘性理论的k-ε双方程组组成的控制方程进行分析[13-15]。上述描述加工区域内不可压缩流体流动的方程如下。

连续性方程为：

(1)

湍动能k方程为：

(2)

耗散率ε方程为：

(3)

式中：ρ—流体密度，kg/m3；μt—湍流黏度，kg/m·s；Gk—平均速度梯度引起的湍动能，m2/s2；Gb—由浮力影响引起的湍动能，m2/s2；YM—不可压缩湍流脉动膨胀对总的耗散率的影响，m2/s3。

湍流黏度：

(4)

k-ε模型中经验常数的取值通常情况下为：C1ε=1.44，C2ε=1.92，C3ε=0.09，湍动能k与耗散率的湍流普朗特数分别为σk=1.0，σε=1.3。

2.2 模型计算

抛光工具盘的几何尺寸如表1所示。

表1 抛光工具盘几何尺寸

本研究在三维实体建模软件中进行布尔运算，得到液动压悬浮抛光流场模型，如图2所示。

图2 流场三维几何建模

图2中，沿着圆周方向周期性地分布着相同的若干单元。本研究选取工件贴片区域的中分线AB作为压力数据提取的参考线。

取抛光加工区域中抛光工具盘与液槽之间的环形流体作为计算区域，计算区域及边界条件如图3所示。

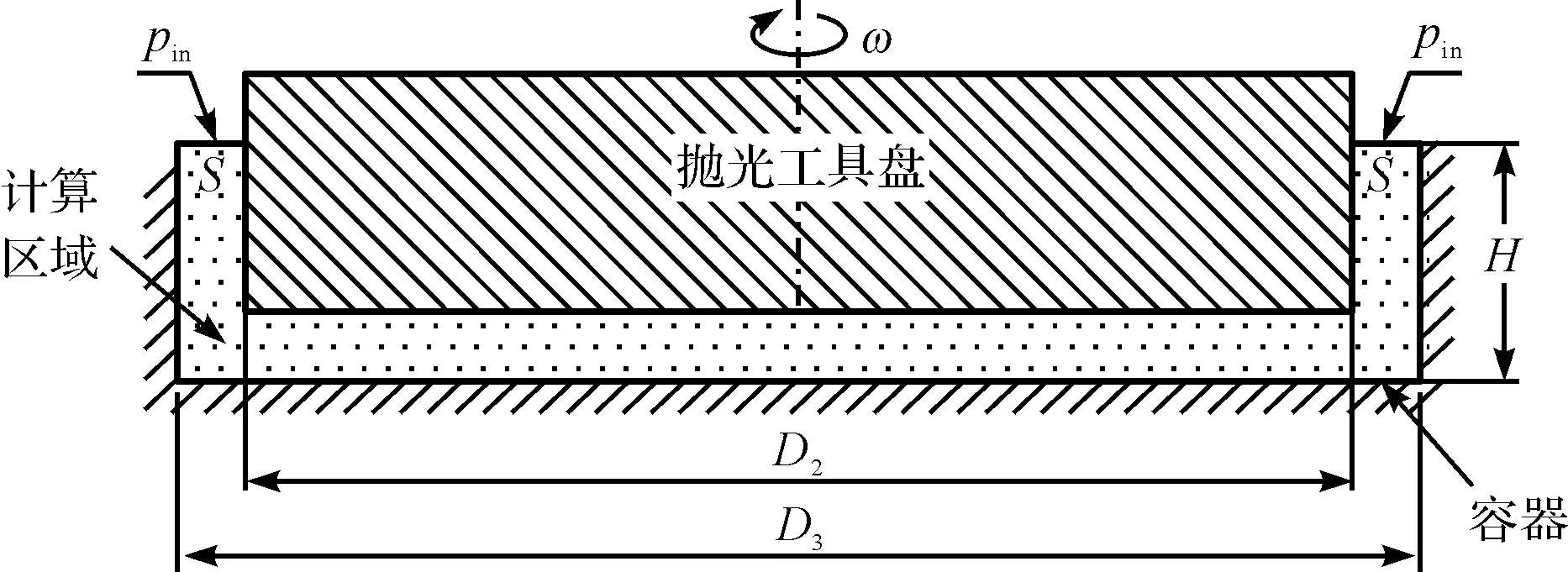
图3 计算区域及边界条件

液槽直径D3=182 mm，液槽高度H=5 mm。根据实际工况，设置边界条件如下：环形表面S设置为压力入口，且Pin=1 atm；抛光工具盘的所有表面设置为旋转壁面；液槽壁面设置为固定壁面。

为实现对加工区流场形态的数值模拟，本文以Fluent14.5为计算平台，采用3D单精度稳态隐式压力基求解器，以及工程上广泛应用的Simple算法进行求解。Simple是求解压力耦合方程组的半隐式方法，它的核心是采用“猜测-修正”的过程，在交错网格的基础上来计算压力场，从而达到求解动量方程(N-S方程)的目的。

3 均匀设计试验和工艺参数优化

3.1 均匀设计试验

流体抛光时液体压力的大小和均匀性对加工效率和质量都有直接影响。由Preston方程可知，被加工工件表面材料去除率与磨粒在近壁区域的相对压力成正比[16]。

根据液动压悬浮抛光特点，本研究选择加工间隙h、抛光工具盘转速ω和抛光液浓度φ作为考察因素。以加工区域的压力大小和压力均匀性为试验指标。具体地说，计算AB线上的压力均值PAVG作为工件区域的压力大小，计算AB线上的压力标准差PSD作为工件加工区域的压力均匀性。

笔者按照3因素7水平的均匀设计表U7(74)及其使用表安排试验，均匀设计方案和试验结果如表2所示。

表2 均匀设计方案和试验结果

本研究对表2中的每组试验参数分别建模，并在Gambit中进行结构化网格划分，将网格文件导入FLUENT中进行边界条件设置，然后进行数值模拟计算，计算得到的抛光工具盘压力分布如图4所示。

图4 液动压悬浮抛光工具盘压力分布

从图4中可以看出：每个单元上内的压力分布相同，在任一单元中，动压力沿周向(蓄流槽-楔形区-平行区-约束边界)方向先逐渐增大后迅速减小，沿径向方向则逐渐增大。

本研究分别提取每组试验参数的AB线上的压力数据，绘制成关于径向坐标的压力分布曲线，如图5所示。

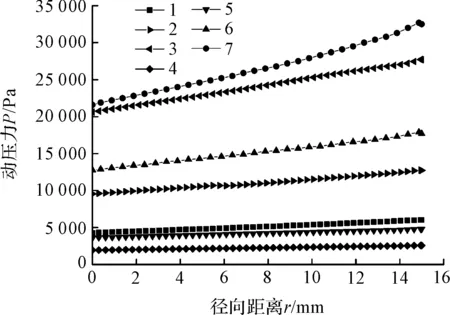
图5 工件区域AB线上压力分布曲线

可以发现，在不同工艺参数组合下，压力沿AB径向方向呈线性分布，符合圆周运动在不同半径上的线速度分布。通过计算，AB线上的压力均值PAVG和压力标准差PSD如表2所示。

由表2结果可知：在不同工艺参数组合下，工件加工区域AB线上的压力均值不同，在4 000 Pa～35 000 Pa范围内变化，且压力标准差也有所不同。这说明工艺参数对压力均值和压力标准差有影响。

由于均匀设计因素水平的选取不具有整齐可比性，无法通过指标观测值直接得到指标与因素之间的关系，需要对表中的数据进行回归拟合再进行分析[17]。

3.2 多元非线性回归模型

本研究采用多元非线性回归方法，分别建立压力均值和压力标准差与加工间隙、转速和抛光液浓度之间的拟合数学模型。

设加工间隙h为x1，抛光工具盘转速ω为x2，抛光液浓度φ为x3。多元二次非线性回归处理多变量参数与目标函数之间的非线性拟合数学关系方程为[18-19]：

(5)

式中：f(x)—目标函数；xj，xi—设计变量，n—设计变量数；β—待定多项式系数。

将表2的数据导入Matlab软件，运用nlinfit拟合，分别得到压力均值PAVG和压力标准差PSD的多元非线性回归方程：

PAVG(xi)=88 524.9-333.1x1-430.3x2+

0.240 38x1x2-2 460.3x1x3-458.336x2x3

(6)

PSD(xi)=91 040.7-333x1-435.6x2+

0.239 99x1x2-2 508.1x1x3-442.458x2x3

(7)

式中：P(xi)—目标函数；x1—加工间隙；x2—加工转速；x3—抛光液浓度。

3.3 基于遗传算法的工艺参数优化

为获得最优工艺参数，本研究采用遗传算法(GA)对多元非线性回归方程进行求解。遗传算法的本质是一种高效、并行、全局搜索的方法[20]。

根据上面建立的加工流场数学模型，相应的优化模型为：

(9)

在Matlab软件中，本研究运用其遗传算法优化模块(GA tool box)对工艺参数进行全局寻优。取f(xi)=PAVG(xi)-PSD(xi)为遗传算法适应的函数，交叉概率与变异概率等参数采用软件默认值，解得h=285 μm，ω=1 300 r/min，φ=0.12。将求解所得的优化工艺参数重新建模，经数值模拟后单元流场的压力云图，如图6所示。

从图6中可以看出：压力沿径向方向呈梯度增大，工件区域的压力比较均匀。

本研究分别提取优化前和优化后径向AB线上的压力数据，如图7所示。

图6 单元流场的压力分布

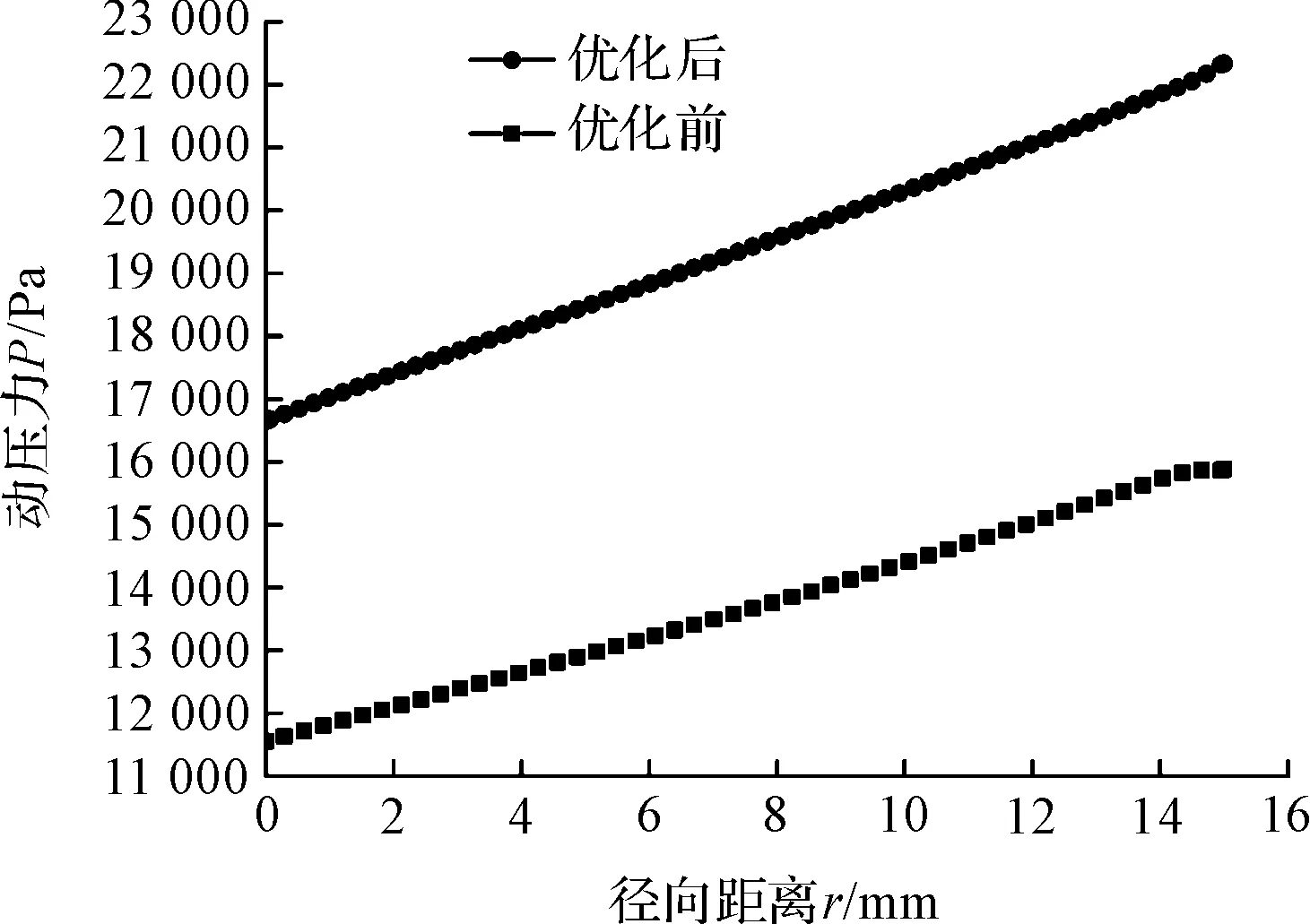
图7 优化前后AB线上压力曲线

本研究计算这两组数据的压力均值和压力标准差，并与回归模型的预测值进行对比，如表3所示。

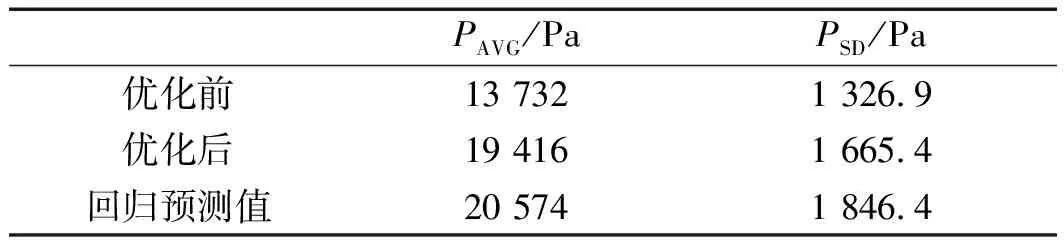
表3 AB线上压力均值和标准差

由表3可知：优化后压力均值提升了41%左右，而压力标准差变化不大，优化后的流场不仅提高了加工效率，而且也有助于加工质量的提高。将优化后的压力均值和标准差分别和回归模型的预测值进行了对比，可以发现压力均值和压力标准差的误差分别为5%和10%，相对比较准确。

4 实验及结果分析

实验是在课题组研发的第二代液动压悬浮抛光装置上进行的，该装置如图8所示。

图8 液动压悬浮抛光装置

试样采用单晶铜，因单晶铜衬底具有导电性好、电流密度分布均匀等优点。试样标准大小为12 mm×12 mm×1 mm，选取机械研磨抛光后粗糙度相近的铜试样进行液动压悬浮抛光实验。

实验分两组对比，即优化前的工艺参数实验1和优化后的工艺参数实验2，不同的加工参数如表4所示。

表4 不同的加工参数

经过0.5 h的液动压悬浮抛光后，两个试样表面粗糙度Ra的测量结果，如图9所示。

图9 优化前后试样的表面粗糙度

从图9中可以看出：试样1粗糙度Ra值为3.88 nm(63 μm×47 μm)，试样2的粗糙度为Ra值为2.35 nm(63 μm×47 μm)。测量结果表明：优化后工艺参数加工的铜试样，其粗糙度比优化前工艺参数加工的铜试样要低，说明优化工艺参数有助于提高试样表面的加工质量，进一步证明了回归模型的正确性，说明该模型可以用来指导工艺参数的优化。