磁流变抛光液制备过程中的气泡动力学模型
2022-05-24李秀红李文辉杨胜强李永刚
郭 策,李秀红,李文辉,杨胜强,刘 佳,李永刚,刘 竞
(太原理工大学 机械与运载工程学院,太原 030024)
磁流变抛光液是一种力学性能受磁场调控的固-液混合智能材料,具有绿色、环保和智能可控等优点,成为磁流变抛光、磁射流抛光以及多物理场辅助液体助喷射抛光的关键介质材料[1-2]。然而,磁流变抛光液制备时容易产生固相颗粒凝聚、结块及沉降等现象[3],必须辅助以颗粒分散工艺进行均质。如何提升现有磁流变抛光液的制备理论及工艺已成为限制其发展的瓶颈问题。
传统的物理分散方法如机械叶片搅拌和球磨搅拌等,耗时长、精度低、可控制差,很难将固相颗粒均匀地分散于基液中[4]。超声波分散利用超声波在液体中产生的空化效应制备悬浮液。空化效应不但能产生剧烈振荡的空化气泡,而且空化气泡在固相颗粒附近溃灭时释放的微射流及冲击波等能够对固相颗粒群起到强烈冲击和高效分散的作用[5]。然而,目前对于磁流变抛光液超声波制备理论研究不足,并不能很好地解释磁流变抛光液的空化效应,特别是气泡在磁流变抛光液中如何产生、发展和溃灭的动力学问题,尚缺乏足够的理论研究基础。
空化气泡运动规律可以用气泡动力学模型来描述。目前成熟的气泡动力学模型主要有Rayleigh模型、Rayleigh-Plesset模型、Keller-Miksis模型、Gilmore模型和Flynn模型等[6-8]。然而,目前的气泡动力学模型主要适用于水溶液或者可近似为水溶液的液体环境,难以直接用于描述固-液混合的悬浮液。近年来,计算流体力学和多物理场仿真技术等在模拟悬浮液声场和流场方面得到广泛应用。但在工程应用中,由于缺乏描述悬浮液的气泡动力学模型,这些数值计算方法往往忽略液体的空化效应,这给悬浮液超声空化效应的理论研究提出了挑战。
论文在经典气泡动力学模型研究的基础上,通过考虑悬浮液的固-液混合作用,建立不同工艺作用下磁流变抛光液的气泡动力学模型,并对超声波制备和机械制备产生的气泡运动进行详细讨论,以期为磁流变抛光液制备工艺提供理论支撑。
1 数学模型
1.1 磁流变抛光液物理环境
磁流变抛光液的一般组成如表1所示。磁流变抛光液的液相主要由去离子水和丙三醇混合形成,它们是磁流变抛光液的主要成份[9]。磁流变抛光液的固相主要由羟基铁粉、绿碳化硅以及少量添加剂组成。羟基铁粉作为典型的磁敏微粒,能够使磁流变抛光液具有明显的流变性和较高的剪切屈服强度。绿碳化硅的加入可以使得磁流变抛光液具有研磨和抛光的作用。添加剂如羧甲基纤维素钠、六偏磷酸钠、亚硝酸钠、无水碳酸钠以及纳米二氧化硅等对固体颗粒起到表面活性的作用,可以在一定程度上抑制固体颗粒在磁流变抛光液中团聚,进而防止固体颗粒发生沉降。
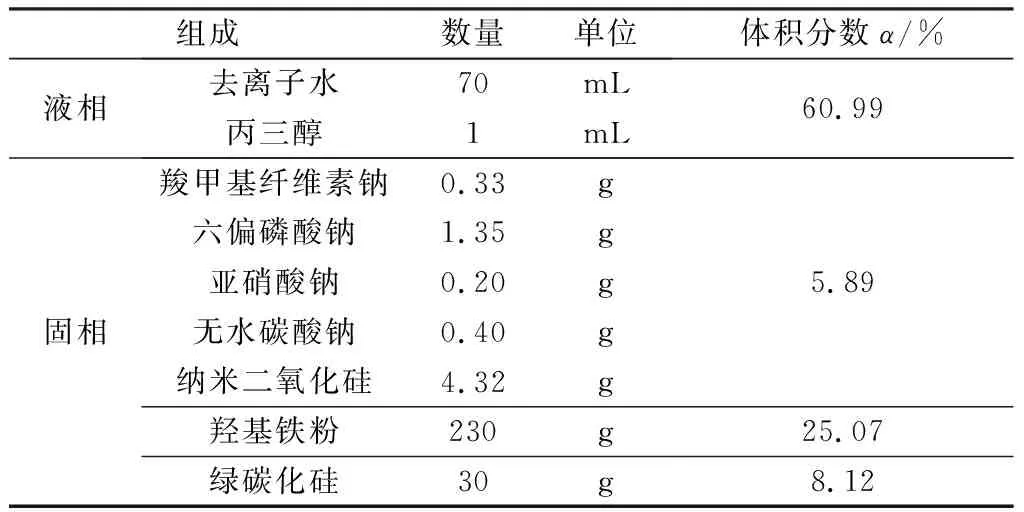
表1 磁流变抛光液的一般组成Table 1 General composition of magnetorheological polishing fluid
由物理环境可知,磁流变抛光液可视为由多种固相颗粒和基液组成的两相悬浮液。磁流变抛光液制备时,固相颗粒在流体压力和速度扰动下快速、均匀地分散于基液中。当固相颗粒粒径很小处于微米或纳米量级时,固相颗粒和液体介质以相同的速度运动。此时,固液两相流可视为强耦合作用,固液两相流运动可近似为单向流运动。为此,引入混合物的连续性方程[10]
(1)
(2)
式中:u为混合物流速;k是相变的种类;φk为体积分数;ρk为每种相变密度。
在未发生空化效应前,忽略微小气核在基液中的体积占比,那么磁流变抛光液的密度ρ可表示为
ρ=φpρp+φ1ρ1.
(3)
式中:φp和φ1分别为固体颗粒和基液所占体积分数;ρp和ρ1分别为固体颗粒和基液的密度。
另外,磁流变抛光液黏度与固相颗粒种类、颗粒几何形状、颗粒质量浓度以及基液配比等均有影响关系,但对黏度起决定作用的还是固相颗粒的体积分数。对于稀薄悬浮液,EINSTEIN[11]给出黏度公式如下
(4)
式中:μ0是基液的黏度;k″为颗粒形状常数,对于球形颗粒,k″=2.5.
然而,式(4)仅适用于固相颗粒体积分数不超过2%的情况,不满足磁流变抛光液的制备需求。VAND[12]在式(4)的基础上提出了高固相颗粒体积分数的黏度公式如下
(5)
式中:α′为颗粒形状第二常数,对于球形颗粒,α′=39/64=0.609.考虑到磁流变抛光液制备过程中对黏度的调控需求,本文引入VAND黏度方程来描述磁流变抛光液的黏度。
1.2 磁流变抛光液气泡动力学模型
磁流变抛光液在工作时通常需要施加外部磁场,并在磁场作用下沿磁感线方向聚集成链状结构。在此条件下,磁流变抛光液是一种高黏性半固态物质。然而,磁流变抛光液制备时并不需要施加外部磁场,此时磁流变抛光液中的固相颗粒应均匀分散于基液中,并表现为牛顿流体。因此,本文讨论的气泡动力学模型适用于非磁场条件下的磁流变抛光液。
磁流变抛光液气泡假设如下:1) 气泡在膨胀和收缩过程中始终保持球形,球形固定;2) 泡内气体为理想气体,考虑泡内气体的等温及绝热过程;3) 计入固-液混合比例,液体不可压缩;4) 不考虑液体热交换、界面相变和化学反应。将磁流变抛光液气泡动力学行为类比为弹簧振子系统,泡内气体对应于弹簧,泡外磁流变抛光液对应于质点。那么泡内气体内能的增加dU就等于磁流变抛光液气泡所做的功dW,即
dU=dW.
(6)
泡内气体内能主要由气泡半径变化产生,表示如下所示[13]
(7)
式中:R为气泡的瞬时半径;r为距离气泡中心的距离。
周围液体对气泡所做的功为
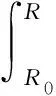
(8)
(9)
式中:pg为气泡泡内压力,pv为泡内饱和蒸汽压,p∞为远场悬浮液压力。
磁流变抛光液气泡泡内压力pg表示如下[14]:
(10)
式中:R0为气泡初始半径;Rmin为气泡最小半径;Rmax为气泡最大半径;γ为气体绝热指数;a为范德瓦耳斯半径(R0/a=8.54).
在磁流变抛光液超声波制备过程中,远场流体压力表示如下
p∞=p0-pasin(2πft) .
(11)
式中:p0为磁流变抛光液静压力;pa为超声波声压幅值;f为超声波频率;t为时间。
同理,在磁流变抛光液机械制备过程中,当流体绕滚筒轴线旋转时,由于离心力作用,悬浮液将产生动态压力,为此远场悬浮液压力表示如下
p∞=p0+ρarr=p0+2ρ(πnr)2.
(12)
式中:ar为旋转流体的平均加速度;r为滚筒半径;n为滚筒转速。
联立式(3)和式(5),将式(7)-(11)代入式(6),得到磁流变抛光液超声波制备过程中气泡动力学模型如下
(13)
同理,联立式(3)和式(5),将式(7)-(10)和式(12)代入式(6),得到磁流变抛光液机械制备过程中气泡动力学模型如下
(14)
1.3 数值模拟与初始条件
利用四阶龙格库塔方法对式(13)和(14)进行数值求解。初始条件如下:t=0时,R=R0,dR/dt=0.磁流变抛光液的计算参数见表1,其中,ρ(羟基铁粉)=7.89×103kg/m3,ρ(绿碳化硅)=3.17×103kg/m3,ρ(添加物)≈1.22×103kg/m3,ρ1=1.00×103kg/m3,其余参数如下:c=1 481 m/s,γ=4/3,pv≈0 Pa,p0=1.013×105Pa,σ=7.28×10-2N/m,μ0=1.005×10-3Pa·s.对于超声波制备,超声波声压幅值pa=0.3×106Pa,而对于机械制备,滚筒半径r=100 mm,滚筒转速n=350 r/min.
2 结果与讨论
超声波制备磁流变抛光液的气泡运动特性如图1所示,其中气泡初始半径R0分别取10 μm、20 μm、50 μm和100 μm.为了分析磁流变抛光液固相成分对空化效应的影响规律,气泡运动特性分为液相和固相+液相两种情况进行讨论。从图1可以看出,磁流变抛光液气泡在一个声周期下历经生长、膨胀、压缩、溃灭及反弹的动力学过程,但基液中固相颗粒对空化气泡运动影响明显。基液中加入固相颗粒后,气泡膨胀幅值明显降低,气泡溃灭时间也会延长,这说明磁流变抛光液固相颗粒的添加明显减弱了液相原有的空化效果。对比图1(a)-(d)可以看出,随着气泡初始半径的增加,气泡膨胀幅值明显减弱,气泡溃灭时间明显延长,并且气泡反弹程度也显著降低,说明磁流变抛光液中较大的气泡并不利于空化效应的产生与发展。这是因为气泡在一个声周期作用下受到超声波负压相和正压相的交替作用,气泡在负压相生长而在正压相收缩。较大的气泡在负压相作用下还没来得及生长到最大,就在正压相作用下开始收缩,因此空化剧烈程度较低。
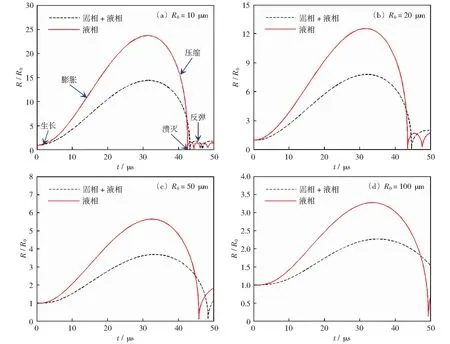
图1 超声波制备磁流变抛光液的气泡运动特性Fig.1 Bubble motion characteristics of magnetorheological polishing fluid from ultrasonic preparation
机械制备磁流变抛光液的气泡运动特性如图2所示,其中气泡初始半径R0分别取10 μm、20 μm、50 μm和100 μm.从图2可以看出,机械制备磁流变抛光液产生的气泡没有发生膨胀,而是直接被压缩之后经历多次反弹,并且随着时间的增加,气泡反弹的幅值越来越小。与此同时,基液中固相颗粒对气泡运动影响明显,基液中加入固相颗粒后,气泡反弹幅值明显增加,反弹周期显著延长,说明对于机械制备工艺,固相颗粒的添加具有提升液相原有空化效果的能力。对比图2(a)-(d)可以看出,随着磁流变抛光液气泡初始半径的增加,气泡反弹的幅值变化不大,但气泡反弹的周期明显延长,这也说明较大气泡并不利于空化效应的改善。
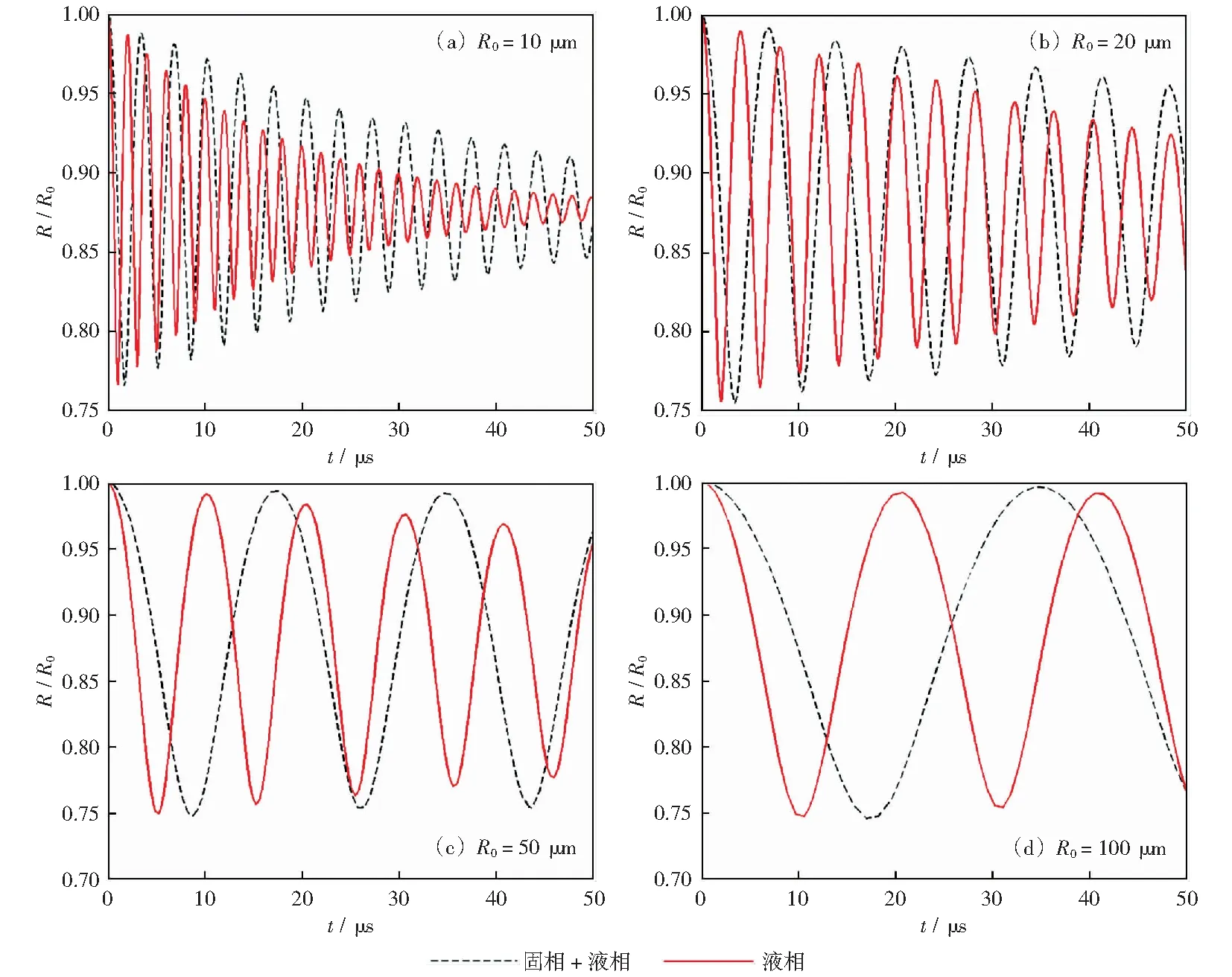
图2 机械制备磁流变抛光液的气泡运动特性Fig.2 Bubble motion characteristics of magnetorheological polishing fluid from mechanical preparation
为了进一步对比超声波制备和机械制备磁流变抛光液空化效应的剧烈程度,图3和图4分别给出了两种工艺作用下磁流变抛光液气泡最大泡内压力和最大泡壁速度。从图3可以看出,不同初始半径的气泡产生的泡内压力高达109量级,随着气泡初始半径的增加,气泡泡内压力逐渐降低。对于超声波制备,基液中加入固相颗粒后,气泡泡内压力会明显降低;而对于机械制备,基液中加入固相颗粒后,气泡泡内压力会逐渐升高。这主要与超声波制备产生的气泡能够历经膨胀、压缩、溃灭及反弹的动力学过程,而机械制备产生的气泡只能经历压缩和反弹有关。从图3还可看出,超声波制备磁流变抛光液产生的气泡泡内压力平均比机械制备的高104量级,说明超声波作用下磁流变抛光液具有更强烈的空化效应。图4给出了两种工艺下磁流变抛光液气泡最大泡壁速度,其规律与图3类似,超声波制备磁流变抛光液产生的气泡泡壁速度比机械制备的高104量级,再次说明了超声波制备磁流变抛光液比机械制备具有更强烈的空化效应。从图4还可以看出,对于不同初始半径的气泡,超声波产生的气泡泡壁速度为104量级;由于当气泡泡壁速度大于声波在基液中的传播速度(c=1 481 m/s)时,气泡会在固体颗粒附近产生高速微射流效应[15],从而对固体颗粒产生强烈的冲击和分散作用,这也是导致超声波制备优于机械制备的微观原因之一。

图3 两种制备工艺下磁流变抛光液气泡最大泡内压力Fig.3 Maximum pressure inside the bubble of magnetorheological polishing fluid under ultrasonic preparation and mechanical preparation

图4 两种制备工艺下磁流变抛光液气泡最大泡壁速度Fig.4 Maximum wall velocity of bubble in magnetorheological polishing fluid under two preparation processes
磁流变抛光液的沉降性是评价其性能的重要指标,可以间接反映颗粒的分散情况[16]。图5给出了超声波制备和机械制备两种工艺下磁流变抛光液的沉降率实验结果对比。其中,磁流变抛光液选择表1的成分和规格进行制备,其余工艺参数如下:超声功率为500 W,超声频率为20 kHz,超声作用时间为30 s;机械搅拌转速为200 r/min,机械搅拌时间3 h;磁流变抛光液沉降0.5~4 h后进行观测。从图5可以看出,磁流变抛光液在观测时间内发生了沉降,随着沉降时间的延长,磁流变抛光液的沉降率s逐渐上升,但相同观测时间t内,超声波制备的磁流变抛光液沉降率远低于机械制备。从本文磁流变抛光液制备过程中气泡动力学的研究发现,与机械制备工艺相比,超声波制备磁流变抛光液中发生了剧烈的空化效应。超声波导致磁流变抛光液气泡历经生长、膨胀、压缩、溃灭及反弹的动力学过程,并且在此过程还产生高达104量级的泡壁速度和109量级的泡内压力,特别是固相颗粒附近还容易产生高速微射流效应,从而对磁流变抛光液固相颗粒产生强烈的冲击和分散作用。而在机械制备工艺下,磁流变抛光液气泡只会做有阻尼的受迫振动,而且气泡泡壁速度和泡内压力较低,对磁流变抛光液固相颗粒的冲击效果有限,因此导致磁流变抛光液的沉降率显著上升。磁流变抛光液的沉降率结果与磁流变抛光液气泡动力学特性分析结果基本一致。

图5 磁流变抛光液的沉降率Fig.5 Sedimentation rate of magnetorheological polishing fluid
3 结束语
采用混合物连续性方程和VAND黏度方程构建了超声波制备和机械制备两种工艺下磁流变抛光液气泡动力学模型。通过对磁流变抛光液气泡动力学模型进行数值模拟发现,与机械制备工艺相比,磁流变抛光液气泡在超声波制备工艺下反应更为剧烈。磁流变抛光液的沉降率实验发现,超声波制备的磁流变抛光液沉降率远低于机械制备。超声波制备磁流变抛光液产生的气泡泡内压力、气泡泡壁速度平均都比机械制备的高104量级,并且超声波制备工艺下的磁流变抛光液更容易产生微射流效应,这是超声波制备工艺优于机械制备工艺的微观特征之一。
