中学生科学理解能力的进阶模型 ——以能量概念为例

姚建欣，郭玉英，阳 熠，曾晨虹，布 兰

中学生科学理解能力的进阶模型
——以能量概念为例

姚建欣，郭玉英，阳 熠，曾晨虹，布 兰

通过融合学科能力体系和复杂度等级模型，从理论上建构了刻画中学生科学理解能力进阶发展的层级模型。选取能量概念作为测试任务的内容载体，以1 033名中学生(8-11年级)为被试，通过对Rasch任务难度值的差异检验和回归分析对此模型进行检验。结果显示：(1)三个发展层级的任务难度平均值依次递增，且各层级间的均值差异显著；(2)回归分析表明任务所属的发展层级能够较好地预测任务的难度；(3)被试的学段和能解决任务的发展层级间存在对应关系。上述结果初步检验了所提出的发展层级，并对课程开发、教学设计和后续的其它概念的学习进阶研究有参考价值。

学科能力；科学理解；复杂度等级模型；学习进阶；能量概念

一、引言

学生发展核心素养指出“关键能力”是基础教育阶段培养工作的重点。能力作为当代教育研究的术语在学缘上带有深刻的心理学印痕，欧洲大陆较广泛认可的对能力的定义源于德国著名心理学家弗朗茨·维纳特：“个体自身具备的或通过学习掌握的、可用以成功且负责任的解决问题的知识、技巧、态度、意志和社交手段。”[1](P4)在教育心理学领域，以林崇德先生为代表的我国学者对能力与各学科学习的融合——即学科能力的建模，也进行了长期的努力并取得了阶段性成果。与新一轮高中课程改革工作并行，紧密结合物理、生物等学科对科学思维等为代表的学科核心素养的凝练，本研究专注分析其中科学理解能力的进阶发展，结合哈佛大学康莫斯(Commons)的复杂度等级模型(Model of Hierarchical Complexity)[2]，尝试对中学生科学理解能力的发展层级进行细致刻画。研究以科学课程中的能量主题为任务载体。选取能量主题首先是因为其在整个科学概念体系中的核心性、发展性和广延性。能量是“所有的科学概念中最重要也是应用最为广泛的物理概念”[3]，贯通从小学到大学的全部科学课程并且一直在发展。对13个发达国家(地区)课程纲领文件的比较发现，“能量”被全部样本国家(地区)列为科学教育的核心概念之一。[4]此外，国内外对能量理解的系统研究已经有30余年的积累，在此基础上开展的学习进阶研究正在引领科学教育研究范式的演变[5]，对中学生能量理解发展研究的突破有助于对其他科学概念研究的跟进。

二、理论基础和研究假设

处于不同发展阶段的被试能够胜任的任务不同，任务的哪些属性是影响任务完成的核心变量一直是认知心理学中任务分析希望解决的核心问题。这些核心变量与人的发展阶段的对应关系也是发展心理学关注的关键议题。国内外学者对学科能力体系以及任务复杂度的分析对解答上述问题提供了一个结构良好的思考角度，并且在任务表现预测上取得了一定成果。由于心理学界对能力体系和复杂度的研究有助于解决学习进阶(Learning Progressions)中进阶变量选取的问题，在国外科学教育界也引起了广泛关注。[6]

任务复杂度起源于对数学问题解决的研究，国内外学者都做出了相应贡献。国外进行相关研究的学者如康莫斯、哈弗德等多属于新皮亚杰学派，但在其研究中展现出受信息加工观点的影响。学者们区分了两种复杂度：水平复杂度(horizontal complexity)和层级复杂度(hierarchical complexity)。[7]前者是指由于信息量的增加而导致的任务难度的增加，后者是指由于起协调作用的非重复动作循环的数量增加而导致的任务难度的增加。例如任务“a+b+c”比任务“a+b”复杂，这是水平复杂度在起作用，而任务“a×(b+c)”比任务“a+b+c”复杂，则是由层级复杂度决定的。对于科学学习任务的解决，水平复杂度有一定的影响作用，但层级复杂度作用更为关键。故本研究以康莫斯等的复杂度等级模型为基础框架，建构中学生科学理解能力的进阶发展层级。

复杂度等级模型是基于信息科学对皮亚杰等的一般阶段模型(General Stage Model)的进一步发展。[8](P120)复杂度等级模型的实质仍是一种阶段理论，但该理论在研究影响任务解决的单维心理构造(unidimensional construct)时有更好的逻辑严密性。复杂度等级模型有三条基本公设：(1)高复杂度的任务是由低复杂度的任务定义的；(2)高复杂度的任务组织或协调了两个以上低复杂度的任务；(3)这种组织和协调关系不是任意的。[9]基于此三条公设可以进一步导出模型的15个复杂度层级，这15个层级涵盖了从最简单的知觉行为阶段到最复杂的跨范式(cross-paradigmatic)思维阶段。

复杂度等级模型具有学科普适性，自提出以来已在包括认知行为分析、推理能力评估等多个领域得到了应用和检验，为各领域的任务分析框架的设计奠定了理论基础，近年来在科学教育领域也得到了初步应用。波恩豪特(Bernholt)等在设计化学学习的任务分析框架时参考了此模型。[6]他们的框架分为五个层级：日常经验、事实、过程、线性因果关系、多变量相关关系，这五个层级对学生的要求依次递增。利用此框架，他们先对化学情境中的任务进行分类，然后检验分类结果在多大程度上能预测Rasch模型得出的任务难度值。结果显示其分析框架能解释57%的方差(F=17.10，p<0.001，R2=0.57)。随后，诺依曼(Neumann)等结合复杂度等级模型以及物理知识分析的“六层级模型”，将复杂度层级概化为四个层级：事实(facts)、映射(mappings)、关系(relations)、概念(concepts)。[10]由此将能量概念理解的四个方面(能量的形式，能量的转移与转化，能量守恒和能量耗散)作为第一级(主要)变量，以复杂度作为次级变量，建构并检验能量概念理解的层级模型。

从综述中可以看到，复杂度等级模型作为结构良好的跨领域任务分析指导框架，在科学教育领域的应用已经取得了初步成果——能够在一定程度上预测化学学习任务的完成难度。然而考察现有科学教育领域对复杂度的研究，仍有三点问题需要注意。第一，他们并没有意识到复杂度研究中应区分任务复杂度和表征复杂度。任务复杂度是由前述的水平复杂度和层级复杂度决定的，表征复杂度则由被试在完成任务时心智模型的建构机制决定，这两种复杂度不能简单地视为等同。有学者指出：必须区分任务复杂度和表征复杂度两个概念，只有在“问题的解决过程中只有一种正确的表征方式时”，两类复杂度才可以直接对应起来。[7]第二，康莫斯等的复杂度等级模型各等级间逐级嵌套关联，本身有极强的逻辑自洽性，并可以和认知发展阶段对应。但两个科学教育团队建构层级框架时并没有和复杂度等级模型严格对应，而是更多地参考了学科本体的知识架构。这致使他们建构的框架中层级间的逻辑关系并不清晰，与认知发展阶段的对应亦不明朗。第三，他们的研究中没有考虑水平复杂度的影响，在开发工具时并未有意识地控制任务的水平复杂度。

基于上述理论分析，本研究对之前科学教育领域建构的科学学习任务的复杂度分析框架进行调整。首先，要在基于领域一般的复杂度模型的同时考虑学习领域的具体特性。科学教育领域的任务类型、问题情境多样，影响变量也较为复杂，鉴于在科学学科能力体系中，科学学习的基础在于科学理解的进阶发展，所以应该首先考察应用复杂度理论体系描述科学理解的进阶发展层级，在此基础上再向其它科学学习任务拓展。在遵循复杂度等级模型的三条基本公设并对应其复杂度等级的基础上，针对研究首先要解决的任务类型和所关注对象的发展阶段，建构了中学生科学理解能力的进阶发展层级，如表1所示。

表1. 科学理解的进阶发展层级、动能概念的示例和对应任务代码

理论预设的中学生科学理解能力的进阶发展层级为三级，分别为：事实经验、映射概括和系统关联，对应科学概念发展的三个不同水平。由表1可以看到，各层级都是通过学生的外显表现界定的。因为国内学者提出的“关系——表征复杂性模型”和国外学习进阶的研究都提示，应该更多地考虑学生认知的实际难度作为任务难度的尺度，而不应该只分析任务本身。所以在划定层级时，我们没有像康莫斯仅用任务描述来界定层级，而是基于预研究中的表现观察、任务分析和访谈，用学生的外显表现来界定层级。

第一级——事实经验，学生解决该层级的任务需基于对现象的感知和具体运算，对应康莫斯的复杂度等级模型的第7级(primary)之前的等级水平，完成小学科学课程的学生应已具备完成该层级任务的能力。第二级——映射概括，顺利解决映射概括层级任务时要求学生对应可观测的物理量建构科学概念，这实质上是要求学生概括并确立抽象概念和具体事物间的映射关系，与康莫斯的复杂度等级模型的第8级(concrete)和第9级(abstract)对应，学习初中科学课程的学生应处于此层级。第三级——系统关联，完成此层级的任务需运用系统性思维，对现象中可能涉及多个变量或多种关系进行加工分析，其实质是对抽象概念的逻辑运算，对应康莫斯的复杂度等级模型第10级(formal)以上的水平，对应的学段是修习高中理科课程阶段。

本模型中高层级的任务是对低层级任务的概括、组织和协调。以动能概念为例，层级2中动能概念的建构基于对层级1中现象的具体感知，而在层级3中对动能Ek与物体质量m和物体在某一参照系中的速度v的平方关系的系统考量，又是以层级2中的建构的动能概念为基础的。虽然以康莫斯的复杂度等级模型为基础，但正如张丽和辛自强发现“平衡称任务的等级复杂性和水平复杂性是完全相关”[11]，实际的科学学习任务中两种复杂性往往也是同时增加的，所以我们的进阶发展层级实际上反映的是水平复杂度和层级复杂度的共同影响。

综上所述，基于理论分析提出了中学生科学理解能力的进阶发展层级。为检验此模型本研究假设：(1)基于此层级模型的任务分析能够预测任务的Rasch难度值，且各层级试题的难度有显著差异；(2)三个进阶发展层级和被试的学段有对应关系。

三、研究设计及方法

研究设计的路线依照“设计框架——开发任务——任务的事前分析——施测——数据分析”进行。为了后续学习进阶研究的需要，在设计开发任务前，选取我国的《义务教育小学科学课程标准》《义务教育初中科学课程标准》《普通高中物理课程标准》，美国的AFrameworkforK-12ScienceEducation和TheNextGenerationScienceStandards，加拿大安大略省的TheOntarioCurriculum：Science等课程标准或教育标准文件进行比较分析，以此为基础确定了如表1“动能概念”所例举的任务设计框架。然后对照任务设计框架设计开发任务，此次测试中的全部任务都是通过纸笔测试完成。随后邀请科学教育专家、教研员和教师对试题与框架的对应性进行讨论，再次确认任务的所属层级。先以J市735名初二到高三的学生作答进行预研究，根据气泡图、试后访谈和Infit指标剔除了部分过于简单、考试作业中练习过的和与Rasch模型匹配度不佳的试题，并以所得的试题难度和被试水平数据作为正式测试编排的依据。

(一)被试及测试安排

本研究选取了J市Y区8-11年级的学生作为测试对象(N=1033)，该区经济发展水平位于J市前列，教育水平(按历年中、高考成绩估算)处于J市中等偏上水平。在该区考务系统的支持下，样本来源的11所学校覆盖了该区的三个学校层次，即市重点校、区重点校和区普通校，班级选择等基本符合等比例随机抽样的要求。由于被试样本覆盖了从8年级到11年级的学生，研究中采用垂直链接(vertical linking)的方法设计链接题，各年级的学生各完成一定数量的链接题，再将全部数据用Winsteps(版本3.72)进行一次Rasch计算，就为各年级被试的能力和全部试题的难度确定了连续的等距量尺，这样各年级被试的能力值和各试题的难度值即可进行比较和差异检验。由于测试时间为开学初(9月17日)，在学生开始学习该年级能量内容之前，可将样本水平看作上一年教学后达成的学生水平。即8年级为学习过小学科学课程，但尚未系统学习初中物理课程的学生水平(小学科学组)，9年级和10年级为学习初中物理课程的学生(初中科学组)，11年级为学习高中物理课程的学生水平(高中理科组)。

(二)测试工具及评卷过程的质量监控

试题以客观题为主，客观题采用0，1计分，选择正确或填出正确答案记为1，多选、错选、错填记为0。简答题按评标的评分档分级计分，由三位参与该课题的研究者独立评分，随后计算肯德尔和谐系数(Kendall coefficient of concordance)来监控评分的一致性。计算发现，W=0.972，p<0.001，表明三位评分者的评分相关性显著，具有高度一致性。各年级间的链接题数量：8、9年级有10道链接题，分别占8、9年级总试题数的50%、45%；9、10年级有12道链接题，分别占9、10年级总试题数的54%、54%；10、11年级有10道链接题，分别占10、11年级总试题数的45%、71%，满足链接题数量和比例的要求。采用Rasch模型给出的指标进行测试工具的质量监控，其给出的“整体指标表”显示：被试信度(person reliability)为0.88，试题信度(item reliability)为0.99。考虑到探索性测试信度值大于0.6即为可接受的信度范围，上述指标表明测试工具的整体区分度(separation)良好，能准确估计学生的能力和试题的难度。“整体指标表”还给出了试题整体难度和被试整体水平的关系，试题难度平均值为系统默认值Mitem=0，被试能力平均值为Mpeople=0.04，表明从整体来看试题的难度适合学生水平。

模型拟合度指标方面，由于本研究的试题跨多个年级，所以应参照样本加权的模型拟合度Infit值。虽然总体样本量为1 033人，但各年级的样本数在250左右，所以应以MNSQ为参考指标，一般认为MNSQ值在0.7-1.3之间可视作与模型拟合良好。本研究模型拟合度指标情况如表2所示，其中绝大部分试题MNSQ值在0.7-1.3之间，有3道题的MNSQ值小于0.7应被剔除，故最后进入分析的题目为35道。综合来看，研究工具较好的符合了质量监控的各项指标。

表2. 测试工具的模型拟合度指标情况

四、结果与分析

(一)进阶发展层级的检验

检验进阶发展层级的前提是“解决系列任务只涉及一个维度的心理构造”，所以首先进行维度检验。Winsteps给出的“标准化残差变异数表”(Table of Standardized Residual Variance)显示，模型(第一个维度)可解释的方差为51%，模型不能解释的方差中，即可能的潜在维度所能解释的方差分别为3%、2.5%、2.4%……潜在维度能解释的方差与第一个维度能解释的方差的比值小于1/10，表明任务解决过程中只有一个主要的心理构造在起作用，这与之前在多个国家的研究所得结论是一致的。[10][12](P128)

根据Rasch模型的计算结果，每个进阶发展层级的试题难度都围绕均值存在一个分布，进行单样本K-S检验发现：各层级试题难度的分布均不符合正态分布，而是成偏态分布。尽管ANOVA被视为非常稳健的检验，偏态分布在样本量充分的情况下不会对F检验结果产生显著影响[13]，但是严谨起见，本研究结合使用非参数检验和方差分析以求得到更稳健的结果。Kruskal-Wallis单因子方差分析是Mann-Whitney U检验的拓展，可以用来检验多于两组的非正态样本间的差异情况。使用SPSS20.0进行分析显示：χ2(2)=517.577，p<0.001，小学科学组的秩均值为177.82，初中物理组的秩均值为575.02，高中物理组的秩均值为755.31。用ANOVA再次讨论上述结果(表3)，仍发现三个层级间的难度平均值依次递增，各层级间的均值差异显著。

表3. 各进阶发展层级试题的难度均值、标准差及组间差异检验的显著性水平和效应值

随后将试题所处的进阶发展层级作为自变量，以Rasch模型估计的题目难度值作为因变量，用介入法进行一元线性回归分析。结果显示：标准化回归系数β=0.828，确定系数R2=0.685，标准误SE=0.035，F(1,34)=74.06，p<0.001，说明进阶发展层级具有预测力，即事前分析划分的任务进阶发展层级能够较好地预测任务的难度。

(二)样本的统计描述

按学生所处学段将各年级被试分为三组：小学科学组、初中科学组和高中理科组。表4中显示的是各年级及总样本的描述性统计参数，由第二列数据可以看到学生能力水平随学段的逐级发展。

表4. 各年级与总样本的描述性统计参数

(三)进阶发展层级与样本的对照比较

基于Rasch模型的数据分析的好处之一是可以将被试能力和任务难度置于同一个等距量尺中进行比较，当某名被试的能力值和某项任务的难度值相等时，意味着该名被试正确解决此任务的概率为50%。据此绘制的怀特图(Wright map)可以使研究者非常直观地观察被试能力和试题难度间的对应关系。图1是加工后的怀特图，怀特图的中间是能力(难度)标尺，怀特图的左边显示被试的群体分布特征，右边显示试题的分布。在被试分布一侧，还用拟合曲线表示出各样本群体的分布：虚线代表小学科学组、点划线代表初中物理组、点线代表高中物理组。在试题分布一侧，用箱图表征不同进阶发展层级试题的难度分布。

从图1中能够看出左侧的群体分布和右侧的试题所属进阶发展层级有对应关系，对表3和表4的描述性统计参数的比照也印证了这一点。具体对应关系为：小学科学组的被试能力(Mability=-2.19)大致与“事实经验”层级的试题(Mdifficulty=-2.93)对应；初中科学组被试能力(Mability=0.51)与“映射概括”层级的试题(Mdifficulty=0.49)对应；高中理科组被试能力(Mability=1.43)与“系统关联”层级的试题(Mdifficulty=1.50)对应。

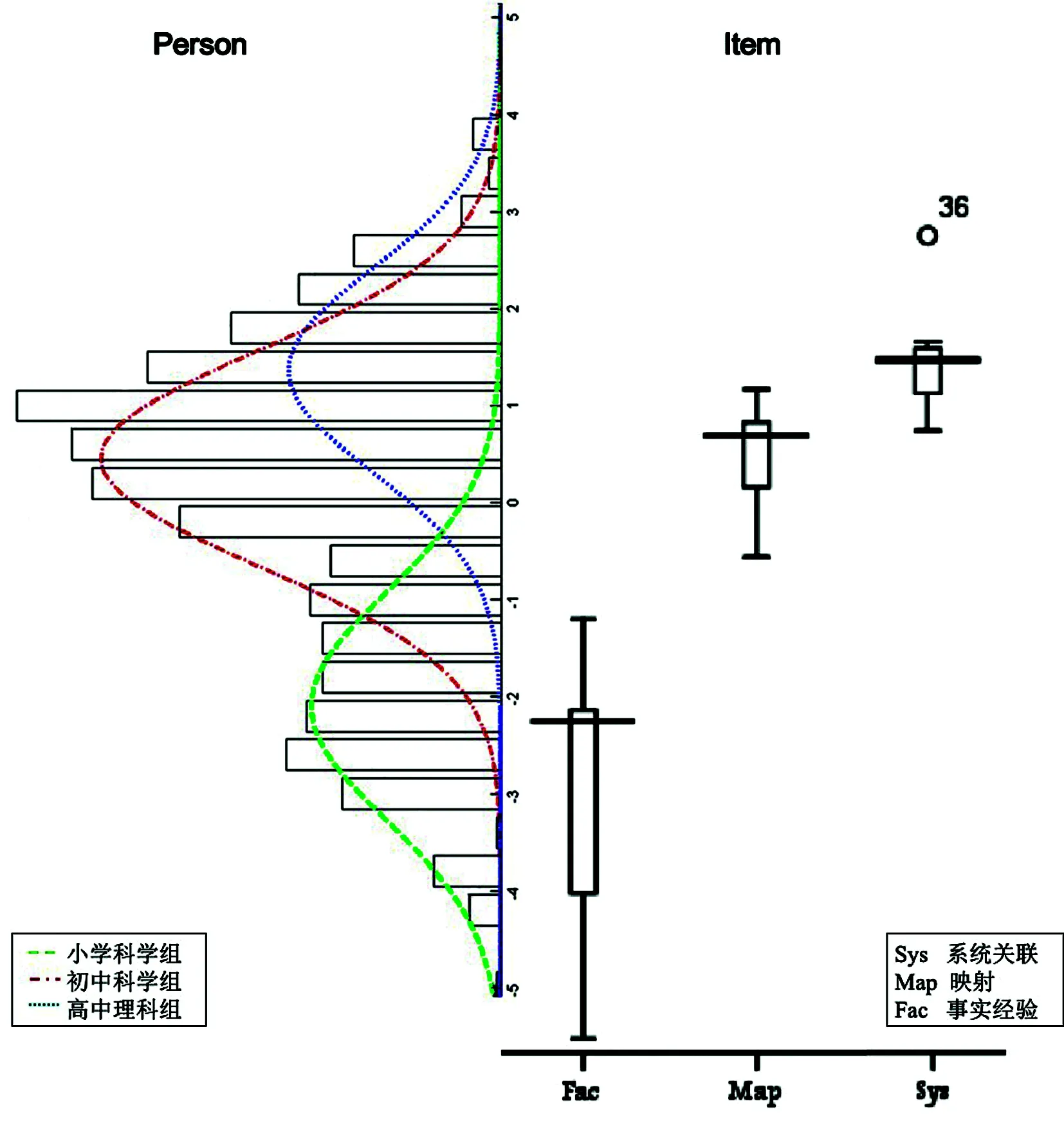
图1 怀特图

五、讨论

上一节中各进阶发展层级间的均值差异检验和回归分析的结果表明：模型的三个层级之间有明显的统计差异，基于模型的事前分析能够较好地预测任务的难度。对照各样本组的统计描述参数和各进阶发展层级的试题平均难度，发现了如理论预设的对应关系。即基于大样本测试初步验证了中学生科学理解能力的进阶发展层级的合理性，由此可以基于此模型进一步分析科学课程内容的难度梯度和进阶次序。这为基础教育阶段的科学课程设计从传统的经验导向到认知导向的转变提供了理论框架，基于此框架进行的大范围科学教学质量检测将为课程设计、教材编写提供实证依据，也能为各阶段的学生评价项目，特别是学业质量标准的设定提供参考。同时值得注意的是，各组样本的能力的分布较广，例如有一小部分初中科学组的学生仍处于事实经验层级，也有部分该组学生已经发展到系统关联层级。这提示我们虽然课程设计主要参照整体发展趋势，但教师在教学设计时应充分考虑学生发展的不平衡性，诊断分析自己的学生以调整教学安排和教学策略。

对于当前科学教育领域的前沿研究议题——学习进阶(Learning Progression)，科学理解的进阶发展层级基于发展心理学的视角提供了新的研究思路[14]。目前国内、外科学教育领域的研究者普遍关注的“进阶”是科学概念中各内容主题间的发展。以本研究中所选取的内容载体能量概念为例，一些研究者认为儿童对能量的理解存在如下发展过程：“先认识能量的各种形式，然后知道能量在各种形式间的转化，再注意到能量是一个守恒量。”[15](P317)据此有研究者对此类“进阶”进行验证。虽然他们都基于大样本测试(如利用TIMSS数据库)并采用相同的研究方法，但除了“认识能量的各种形式”比其他内容更容易外，研究者并没能在这类“进阶”的其它次序上达成一致。[5][10]能量概念各内容主题间的“进阶”没有得到实证研究的支持，证伪了之前的假设。并且其次序的不稳定性和不显著性使我们有理由怀疑，这条“进阶”主线上的难度递进只是学生科学概念发展的一种表象，而复杂度的增进才是科学概念学习进阶的核心变量。而且，对比分析科学理解的进阶发展层级和传统“进阶”假设可以发现，进阶发展层级模型能够解释传统“进阶”的有效部分：“认识能量的各种形式”主题内容的总体难度比其它主题低，正是因为该主题包含大量低发展层级的内容。

由此，我们可以拓展和深化学习进阶研究中的进阶变量(progress variable)的选取与设计工作，即基于发展心理学和认知科学的相关理论来选取和设计进阶变量，刻画处于不同发展阶段的学生所能胜任的任务水平，进而为课程开发和教学设计提供参考。对于学习进阶研究而言，上述对进阶变量的探索也在推动着其研究范式的发展演变：从以知识内容本体为中心的验证性研究向着以学生认知发展为中心的循证性研究。由此，学习进阶研究将不再限定于一个知识主题之内开展，而是能对跨学科概念的理解、学科能力的发展等进行探索。随后，若能将各方面的进阶路径进行整合并加以实证检验，将能实现对核心素养发展脉络的系统设计，且有助于其在课程、教学与评价中落地。

反思整个研究过程，必须承认面对科学概念学习这种复杂的认知活动，本研究设计时重点关注了复杂度的增进，不得不将一些次要影响因素(如情境变量等)视为了干扰测量结果的“噪音”而加以忽略。另外，研究的结果还显示出复杂度水平划分“颗粒度”还值得进一步细化。例如在怀特图(图1)中可以看到“事实经验”层级任务的难度跨度比较大，这启示在补充低年级组被试后可以尝试对此层级进一步细分。最后，我们还关注到近年来成人被试在更高进阶发展层级的认识发展的研究进展[16]，而本研究中最高端的被试仅止于高二年级的学生，可以预想对各年级文、理科大学生的研究将会带来一些有意义的研究结果。课题组将在后续研究中对这些新的研究问题进行探索。

[1] Weinert, F. E.Concepts of competence[R].Neuchtel:Organization for Economic Co-operation and Development,1999.

[2] Commons, M. L.Introduction to the model of hierarchical complexity and its relationship to postformal action[J].World Futures,2008(64).

[3] Nordine, J., Krajcik, J., & Fortus, D.Transforming energy instruction in middle school to support integrated understanding and future learning[J].Science Education,2011(4).

[4] 谭晓.中学生对物理学科中能量概念认识状况的调查研究——以北京市两所中学为样本[D].北京:北京师范大学，2010.

[5] Liu, X., & McKeough, A.Developmental growth in students' concept of energy: Analysis of selected items from the TIMSS database[J].Journal of Research in Science Teaching,2005(5).

[6] Bernholt, S., & Parchmann, I.Assessing the complexity of students' knowledge in chemistry[J].Chemistry Education Research and Practice,2011(2).

[7] 辛自强.关系-表征复杂性模型的检验[J].心理学报,2003(4).

[8] Commons, M. L., Richards, F. A., & Armon, C. Beyond formal operations: Late adolescent and adult cognitive development (Vol. 1) [M].New York: Praeger,1984.

[9] Commons, M. L., Trudeau, E. J., Stein, S. A., et al.The existence of developmental stages as shown by the hierarchical complexity of tasks [J].Developmental Review,1998(3).

[10] Neumann, K., Viering, T., Boone, W. J., et al. Towards a learning progression of energy[J].Journal of Research in Science Teaching,2013(2).

[11] 张丽,辛自强.平衡秤任务复杂性的事前与事后分析[J].心理发展与教育,2008(2).

[12] Liu, X., & Boone, W. J.Applications of Rasch measurement in science education[M].Maple Grove, MN: JAM Press,2006.

[13] Glass, G. V., Peckham, P. D., & Sanders, J. R. Consequences of failure to meet assumptions underlying the fixed effects analyses of variance and covariance[J].Review of Educational Research,1972(3).

[14] 姚建欣,郭玉英.为学生认知发展建模:学习进阶十年研究回顾及展望[J].教育学报,2014(5).

[15] Driver, R., Squires, A., Rushworth, P., et al.. Making sense of secondary science: Supporting materials for teachers[M].London: Routledge,1994.

[16] Commons, M. L., Goodheart, E. A., Pekker, A., et al.Using Rasch scaled stage scores to validate orders of hierarchical complexity of balance beam task sequences[J].Journal of Applied Measurement,2008(2).

MiddleSchoolStudents’ProgressionModelofScientificUnderstanding:——Taking Energy Concept as an Example

YAO Jianxin, GUO Yuying, YANG Yi, ZENG Chenhong, BU Lan

Through fusing the system of subject competence and the Model of Hierarchical Complexity, the progression model of middle school students’ scientific understanding was constructed in theory. The model was testified by selecting 1033 students (grade 8 -grade 11) as subjects and energy concept as the content, and difference testing and regression analysis on difficulty value of Rasch task. The results show that: (1) the mean of 3 development levels’ task difficulty increases successively, and there are significant differences between each two levels; (2) the regression analysis can predict the difficulty of tasks. (3) a corresponding relation between students’ phase of studying and the progression levels is found. Results above verify the progression levels proposed, and have reference value for curriculum exploitation, teaching design and the subsequent learning progression study of other concepts.

subject competence; scientific understanding; the Model of Hierarchical Complexity; learning progressions; energy concept

G633.7

A

1009-7228(2018)01-0066-07

10.16826/j.cnki.1009-7228.2018.01.014

姚建欣，郭玉英，阳熠，等.中学生科学理解能力的进阶模型——以能量概念为例[J].天津师范大学学报 (基础教育版)，2018(1).

2017-10-20

姚建欣，教育部基础教育课程教材发展中心(北京 100029)教材处助理研究员，博士；郭玉英，北京师范大学物理学系教授，博士，博士生导师；阳熠，北京师范大学物理学系硕士研究生；曾晨虹，北京师范大学物理学系学生；布兰，北京师范大学物理学系学生。

教育部人文社会科学研究规划项目“基于科学概念学习进阶的教学设计模型研究”(13YJA880022)；国家级大学生创新创业训练计划创新训练项目“高中生能量概念学习进阶研究”(201310027032)。

岳俊冰]