一道平面几何竞赛题的解法展示与简析——命题者思路与学生解题思路的差异

江西省瑞金第一中学 (342500)

谢小平 杨祖华 许丽美

2018年全国高中数学联赛江西省预赛已经落下帷幕，笔者有幸参加了今年赣州市的阅卷工作，发现这道平面几何题很值得研究与思考.

题目如图1,ΔABC的内心为I,D,E,F分别是边BC,AC,AB的中点，证明：直线DI平分ΔDEF的周长.

让我们先来看命题者提供的解题思路：

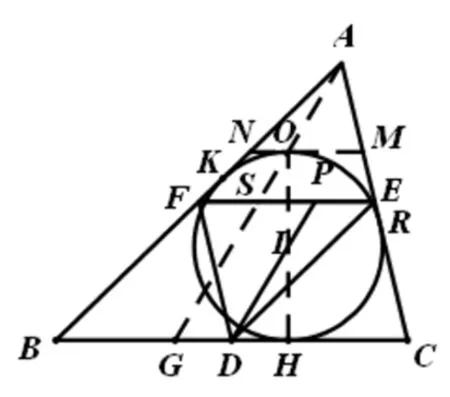
图1

证明：作出ΔABC的内切圆⊙I分别切BC,AC,AB于H,R,K,连接HI并延长交⊙I于O,过O作BC的平行线分别交AC,AB于M,N,连接AO并延长交BC于G,设AG交EF于S.

又D,E,F分别是边BC,AC,AB的中点,∴AB=2DE,AC=2DF,BD=CD,BG=2FS,CG=2ES,∴2DE+2FS=2DF+2ES,∴DE+FS=DF+ES.

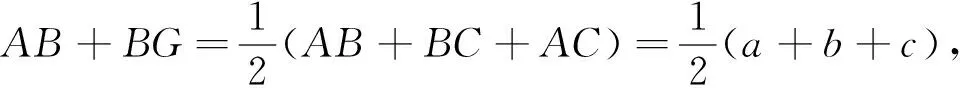
从命题者提供的参考答案容易看出，命题者的思路应该是来源于旁切圆的性质，即AO会平分ΔANM的周长，从而推导出一系列的等分周长的性质，进而得到此题的证明.但在实际的阅卷过程中，使用这种方法进行证明的学生是凤毛麟角，大部分学生利用的是内心、角平分线的性质和相似三角形的关系进行证明,以下三种解法是在改卷过程中学生给出的解答.

图2

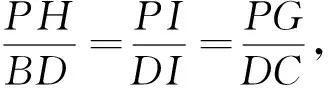
图3

对ΔARQ及D,I,P′三点由梅涅芳斯定理,有

合.即P为ΔAEF内切圆在EF上的切点,∴PE+AF=PF+AE,又AF=DE,AE=DF,∴DE+EP=DF+FP,即直线DI平分ΔDEF的周长.

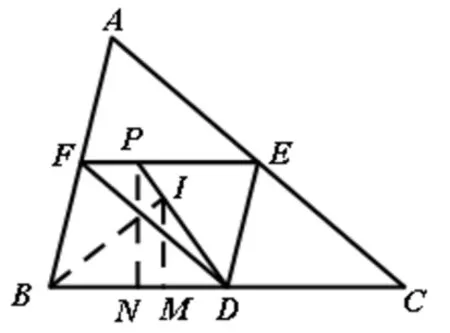
图4

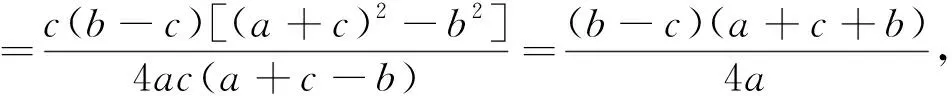
由于命题者在试题的图形绘制中，隐去了三角形的内切圆，所以，几乎没有考生严格按照命题者给出的标答证题.但从以上考生的几种证法可以看出，其证明过程都优于命题者，“教学相长”我们应该遵循这一教学规律.