提升建模素养 驾驭数学高考

安徽淮北师范大学数学科学学院 (235000)

张雨彤 张 昆

数学模型是一种运用数理逻辑方法和数学语言建构的数学模式，也是解决问题的重要途径.通过建立数学模型，可以培养学生的应用意识，锻炼学生从现实的生活背景中提炼相关的数量关系，提出问题，综合与灵活地应用所学的数学知识、思想方法，用数学语言表达出来，选择有效的方法和手段分析信息，进行独立的思考、探索和研究，提出解决问题的思路，将现实问题转化为数学问题，并加以解决.依据2017年新版《普通高中数学课程标准》建议，数学建模是对现实问题进行数学抽象，用数学语言表达问题、用数学方法构建模型解决问题的素养，这更是将数学建模素养放在了高中数学更为重要的地位上.所以，将数学与客观实际问题联系起来，通过实际问题抽象出数学表达式，并能够联系实际求解模型，应用模型，也一直是高考考查的热点问题.

一、已知模型求解问题

根据解决的实际问题不同，数学模型多种多样，包括概率模型、线性回归模型、三角函数模型等等.然而本质上，数学模型就是系统的某种特征的本质的数学表达式(或是用数学术语对部分现实世界的描述).所以，在题目已给数学表达式的情况下，直接用求解函数的思路去思考求解数学表达式即可.

(1)当x在什么范围内时，公交群体的人均通勤时间少于自驾群体的人均通勤时间？

(2)求该地上班族S的人均通勤时间g(x)的表达式；讨论g(x)的单调性，并说明其实际意义.

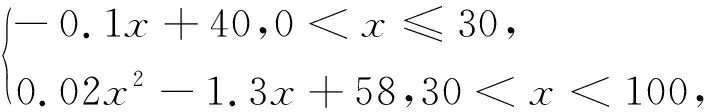
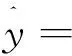
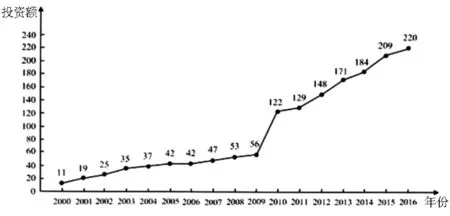
图1

(1)分别利用这两个模型，求该地区2018年的环境基础设施投资额的预测值；

(2)你认为用哪个模型得到的预测值更可靠？并说明理由.

说明：高中阶段，为了更好地将实际问题与数学问题相联系，朝着建模迈出的第一步，就是将问题情境化，联系数学模型与现实实际问题，这样把数学情境化的尝试可以让数学更有现实关联性且更有趣[2].每一个数学模型，它的实际意义可能有许许多多，就像之前学过的导数定义是实际问题中所有变化率在数学上的反映一样，同一个数学表达式可以被赋予很多的现实意义，所以，在模型的预测值判断上，一定会选择用数学表达式计算出偏差较小的那个值.

二、依据信息建立模型

数学建模完全不同于其他数学分支，它不是“学”数学，而是“学着用”数学.数学建模是把数学和客观实际问题联系起来的纽带.所以，在解高考题时，可以通过对题目中的信息进行整理与分析，找出其中的内在规律，抓住问题的主要矛盾，提出假设，经过抽象简化，建立反映实际问题的数量关系式(数学模型)，然后运用数学的方法和技巧创新地分析和解决问题.

例3 (2018江苏卷·17)某农场有一块农田，如图2所示，它的边界由圆O的一段圆弧MPN(P为此圆弧的中点)和线段MN构成.已知圆O的半径为40米，点P到MN的距离为50米，先规划在此农田上修建两个温室大棚，大棚Ⅰ内的地块形状为矩形ABCD，大棚Ⅱ内的地块形状为△CDP，要求A，B均在线段MN上，C,D均在圆弧上，设OC与MN所成的角为θ.

图2

(1)用θ分别表示矩形ABCD和△CDP的面积，并确定sinθ的取值范围；

(2)若大棚Ⅰ内种植甲种蔬菜，大棚Ⅱ内种植乙种蔬菜，且甲、乙两种蔬菜的单位面积年产值之比为4:3，求当θ为何值时，能使甲、乙两种蔬菜的年总产值最大.

说明：当我们面临实际问题时，一般情况下，对于学生而言，相对来说问题所提供的信息杂乱无章，不是轻而易举就能理出头绪的.要想真正解决实际问题，就必须通过意识机能、支点信息生成结构轮廓、记忆库知识框架对比等一系列作用(如图3所示)[3]，这种知识框架其实就是数学模型，找到了恰如其分的数量关系式(数学模型)来表示，然后再通过模型求解与分析，运用数学的方法和技巧创新地分析和解决问题.

图3

例4 (2018全国高考数学卷Ⅰ·20)一箱产品在交付用户之前要对产品作检验，如检验出不合格品，则更换为合格品.检验时，先从这箱产品任取20件作检验，再根据检验结果决定是否对余下的所有产品作检验.设每件产品为不合格品的概率都为p，且各件产品是否为不合格品相互独立.

(1)记20件产品中恰有2件不合格品的概率为f(p)，求f(p)的最大值点p0.

(2)现对一箱产品检验了20件，结果恰有2件不合格品，以(1)中确定的p0作为p的值.已知每件产品的检验费用为2元，若有不合格品进入用户手中，则工厂要对每件不合格品支付25元的赔偿费用.

(ⅰ)若不对该箱余下的产品作检验，这一箱产品的检验费用与赔偿费用的和记为X，求EX；

(ⅱ)以检验费用与赔偿费用和的期望值为决策依据，是否该对这箱余下的所有产品作检验？

为二项分布，设一箱产品花的费用为X，则其分布列如下.

X025P910110

说明：概率模型只是数学模型中的一个类型，想要真正驾驭高考数学，必须要在头脑中建立一个完整的数学建模体系.建立数学模型的一般步骤如下：(1)提出问题并用准确的数学语言加以表述；(2)分析各种因素，依据题目找出内在规律；(3)建立数学表达式(数学模型)；(4)按数学模型进行数学推导，得出有意义的数学结果；(5)对数学结论进行分析，若符合要求，可以将数学模型一般化和体系化，应用在数学预测等多种数学功能中.

三、结语

建模素养是考核数学应用的一项核心素养，它是通过将理论性的数学知识应用于现实世界中的过程，培养学生的数学思维能力，并且经由此，展示学生的实用性价值，在高考试题中渗透广泛，要引起广大数学教师的高度重视，并设法在教学设计中渗透这种数学建模思想意识，启发学生形成具体的数学建模技能，积累数学建模的经验.因此，在高三数学复习教学中，引导学生在一些实际问题上去发现问题，提出问题，建立数学模型求解，最后解决问题，可以帮助学生应对与驾驭数学高考.对此，我们高三数学教师应该思之再思，慎之又慎！