探高考题解法 谈数学核心素养之计算能力培养
2018-12-28北京市第八十中学100102
北京市第八十中学 (100102)
孙世林
2018年北京高考文科20题是一道解析几何考题,综合性强,能力要求高,全面深入地考查了解析几何的知识本质,同时也很好地体现了对数学核心素养之数学运算的考查;在高考中考生虽然解题思路较为清晰,但考生却普遍失分较多,究其原因主要是数学运算的问题,解析几何的知识本质是用代数的方法研究几何问题,所以运算能力成为了解决解析几何问题的必备能力,下面通过2018年北京高考文科20题解法的探究,谈谈在解题过程中如何把握代数运算,完善解题过程.
一、考题再现

图1
(1)求椭圆M的方程;
(2)若k=1,求|AB|的最大值;

二、解法探究

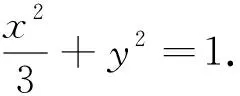

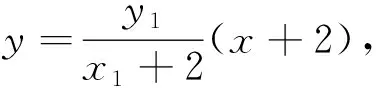



点评:解析几何综合问题常为在运动变化过程中探究某些不变的性质与规律,对于这类运动变化问题,解题时要深入探究产生运动变化的根源,从产生运动变化的根源入手,自然快捷地解决此类问题.另外,解析几何较欧氏几何,最大的优势是把“运动变化引入几何”,实现了“用坐标刻画运动”;这种用代数手段来研究几何问题的伟大构想就是解析几何的本质,所以代数运算是解决解析几何问题必须经历的过程,并且有的代数运算是相当繁琐的,所以在平时的学习中要有意识强化代数运算,提高我们的计算能力.
分析2:在第三问中,可以理解为从点P(-2,0)作两条直线分别与椭圆M依次交于C、A和D、B,求点C、D、Q共线时AB所在直线l的斜率,所以过点P(-2,0)作两条直线是本题中的运动变化的根源,因此解决本题从PA、PB入手,设PA所在直线方程为y=k1(x+2),PB所在直线方程为y=k2(x+2),借助C、D、Q共线,寻求点A、B坐标的关系,从而求出直线AB的斜率.
解法2:(1)(2)略.

(1+3k1)x2+12k1x+12k1-3=0,则x1+x3=

点评:解析几何的核心方法是用代数的方法研究几何问题,在解题过程中,首先要将文字信息、图形条件进行对比互补,用恰当的代数语言描述几何要素及其关系,将已知的几何条件表示成代数形式,然后进行适当的的代数运算得出代数结果,最后通过分析代数结果的几何含义解决几何问题,在这个过程中要经历文字信息、图形特征和符号语言之间的多重转换,但无论怎么转化代数运算的结果的正确与否直接关系解题的成败,所以重视代数计算,提高数学核心素养之计算能力的培养是解析几何教学中必须引起重视的重要环节.
分析3:对于“直线与圆锥曲线的综合问题”,通常将直线方程和曲线方程进行联立,消元后得到一个一元二次方程,再结合韦达定理、根的判别式等来处理相关问题,这似乎成为了解决圆锥曲线综合问题“通用”的解题策略,其本质就是相关“点”是直线与圆锥曲线的“公共点”,从而转化为方程组的解,借助方程组的解来探究题目中的几何关系;但这种“通用”的解题策略有时会有较为繁琐的解题过程,深入思考此种方法,可以直接将点的坐标代入圆锥曲线或直线方程,再借助“点坐标”这一代数形式下的运算实现对题目中几何关系的探究,避免了解方程组的繁琐,从而简化运算.
解法3:(1)(2)略.


点评:此种解法避开了解决圆锥曲线综合问题“通用”的“联立方程、消元、韦达定理、根的判别式”解题策略,由于题目中相关的点是椭圆和直线的公共点,此种解法充分抓住了这些点的坐标满足相应的方程的特点,从而转化为这些点坐标间满足的关系,在寻求这些坐标间的“相关联之处”,从而解决此题;此法很好地体现了解析几何的本质,即“用坐标刻画运动,用代数方法来研究几何问题”.
三、反思
圆锥曲线是一个几何图形,圆锥曲线问题中包含了一系列的几何关系,怎样才能更好地研究这些几何图形中的几何关系,数学中引入了“解析法”,其核心是用代数的方法研究几何.在解决解析几何问题时,要借助平面直角坐标系,将平面内的“点”与“数对”之间建立一一对应的关系,要深入探究用什么样的代数形式表示题目中的几何关系,再通过对代数关系的研究,实现研究几何图形性质的目的.
学习解析几何的拦路虎之一就是代数变换的繁琐、冗长,需要较强的运算能力.解题过程中,许多学生都是因为不能顺利进行代数变换而导致失败.而高中数学课程中明确提出应注意提高学生的数学思维能力,这是数学教育的基本目标之一,其中运算求解、数据处理能力就是数学思维能力的具体体现,考纲中也明确提出了考查学生的运算求解能力和数据处理能力的具体要求.因此,教师不要将计算结果直接给出,在课堂上和复习中应舍得花时间和学生同甘共苦经历计算的过程,向学生阐述每一步计算的算理,提醒学生注意每一个计算细节,区分不同参数的地位作用,教给学生重要的代数变换方法和必备的计算技巧,运算能力的提高是一个长久且螺旋式上升的过程,教师要注重对学生进行算法、算理的引导,教师要结合学生的实际有意识的设计一些开放性问题让学生去探究,培养学生耐心细致的运算习惯,培养学生的意志力,教育学生要有信心、耐心、信心和恒心,同时引领学生根据有关“形”的特征尽量减少运算,充分利用定义、形的特征简化运算,相信学生的运算能力一定能提升,使得学生解决解析几何问题更加得心应手.
解析几何中涉及直线与圆锥曲线的综合问题一直是高考、高校自主招生及各类竞赛的热点、难点、重点,尤其面对繁琐的步骤及复杂的计算,往往令学生束手无策,甚至产生畏惧心理.在教学实践中,学生往往真奔主题,强行求解,这样不仅花费了大量宝贵时间,而且往往因为字母多、步骤繁、计算量大导致精神紧张、体力透支、推理出错,出现绝大多数学生半途而废甚至无功而返的尴尬局面.上述解法探究,重点在如何恰当利用题目中的几何条件、如何优化解题过程、怎样细化代数运算的探究,特别是代数运算的关键环节的处理做了深入细致的分析,希望能给同学们的解题带来帮助.
