一道高考立几选择题的多解剖析

江西省临川二中 (344100)

黄卫民

2018全国一卷理科第12题：

已知正方体的棱长为1，每条棱所在直线与平面α所成的角都相等，则α截此正方体所得截面面积的最大值为( ).

分析：这道题是出自必修2的研究性课题正方体中有关截面问题的改编题,本题以学生最为熟悉的正方体为背景，求与正方体棱所成角相等的截面面积的最大值，解决本题的几个关键环节分别是：确定截面的方向和形状，明确截面面积何时取得最大值，最后求出最大值.

解法一：因为一组平行线与已知平面所成的角都相等，而正方体有12条棱，共构成三组平行线，故每条棱与截面所成的角可化归为同一顶点出发的三条棱与截面所成角.根据经验能直观感知到平面AB′D′是符合要求的平面(图1)，由对称性可知，平面BDC′也是符合要求的平面(图2)，且与平面AB′D′平行的平面都与这三条直线所成角相等.

根据以上分析，易知该截面的形状为：由小变大的正三角形——六边形——正六边形——六边形——由大到小的正三角形.根据基本活动经验学生可以判断(或猜想)出当截面形状为正六边形时，截面面积应该最大(图3).

图1 图2 图3

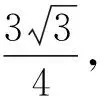
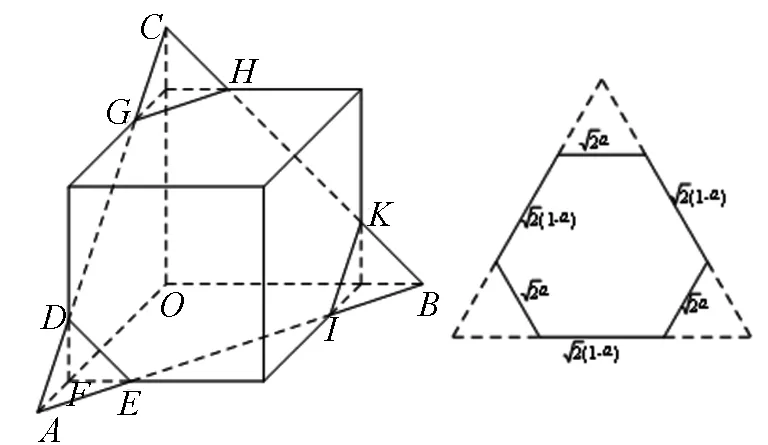
图4 图5

点评：解法二的计算对截面形状的判断要求很高，尤其是截面六边形在正三角形内学生不易想到，可考虑将截面积的计算问题转化为投影面的计算，将问题简化，于是有解法三.

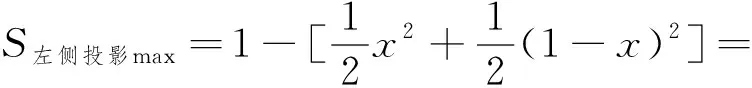
对于空间感不强，空间位置判断不好的同学，也可以考虑用空间坐标系来寻找解决方法.

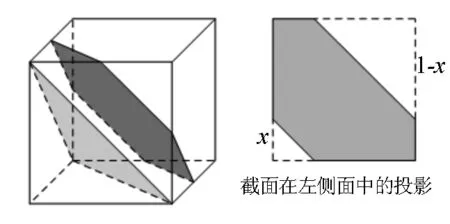
图6

图7

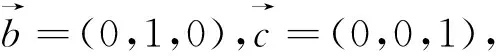
结语：本题以正方体为背景，通过求与正方体棱所成的角相等的截面面积的最大值这一问题，综合考察了学生分析问题、数学抽象、猜想论证、数学建模、函数最值的求法等多种知识和能力.