一道探究题的多种解法和推广
2018-12-28江苏省启东市汇龙中学226200
中学数学研究(江西) 2018年12期
江苏省启东市汇龙中学 (226200)
袁 琴
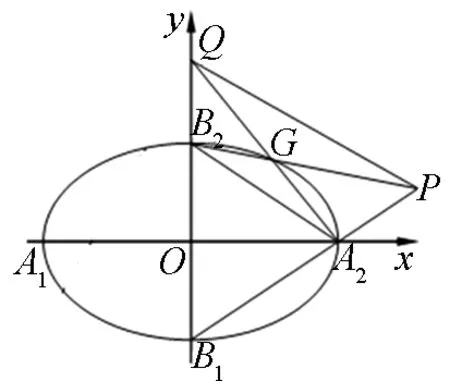
图1
(1)求椭圆C的方程;
(2)设G是椭圆C上除顶点外的任意一点,直线A2G交y轴于点Q,直线A2B1交B2G于点P.探究直线PQ是否过定点?若过定点,求出定点;若不过定点,说明理由.




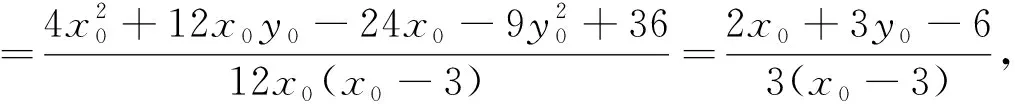
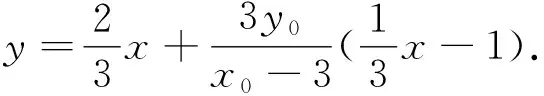


法三:通过特殊化求出定点,然后证明.
当G趋向于点A2时,直线A2G趋向直线x=3,点Q无穷远,点P趋向于点A2,所以直线PQ为x=3;当G趋向于点B2时,直线A2G趋向直线A2B2,点Q趋向于点B2,直线B2G趋向直线y=2,所以直线PQ为y=2.
这样的过程知易行难,所幸无论是我们的手指,还是现代制琴工艺,都允许我们弹奏出美妙的“极弱音”,剩下的只是我们对于拓展美妙音色的意愿,因为作为钢琴演奏家,我们能够,也理应如此。
由此可见,二直线的交点为(3,2),所以直线PQ过定点(3,2).
下面证明直线PQ过定点M(3,2).


结论1的证明仿上述法三的证明,这里从略.

图2

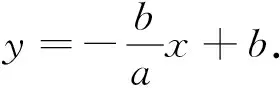

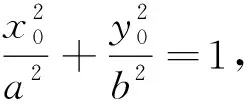

图3






