不同照明条件下全息图的衍射场分析
2018-12-27丁文革杨晨鹤代秀红张荣香
丁文革 杨晨鹤 代秀红 张荣香
(河北大学物理科学与技术学院,河北 保定 071002)
光波经过光学系统后形成的波场,一般是比较复杂的。现代光学的思想就是要在复杂的波场中分离出简单的波动成分:平面波和球面波。由于波场的主要特征体现在波前函数的相因子中,因此可以根据波前函数的相因子来判断波场的性质,分析衍射场的主要特征,这就是所谓的波前相因子判断法[1,2]。在2015 全国高等院校光学教学暨学术研讨会上,北京大学钟锡华教授曾积极倡导采用波前相因子判断法分析复杂波场的主要成分[3]。实际上在很多场合,只需掌握衍射场的主要特征就够用了,在全息技术中就是如此。
全息技术是利用干涉和衍射原理记录并再现物体的真实三维图像技术,现在已经广泛应用于不同的领域[4-6]。但是在一般光学教材中介绍全息再现时,总是说“用一束同参考光的波长和传播方向完全相同的光束照射全息图,就可以还原出物体的样子”[7-9]。 那么,如果采用与参考光波不同的照明光波,结果如何呢?这里将采用波前相因子判断法,对不同照明条件下全息图的复杂衍射场进行详细解析,识别出再现波场中与物光波相关的信息,并用图示法把再现图像的分布情况表示出来。这不仅有助于我们深入理解全息再现图像的特点并应用于不同的实际需求中,而且有助于我们以后更好地利用波前相因子判断法,处理复杂波场问题。
1 理论基础
φ(x,y)=k(sinθ1x+sinθ2y)
(1)
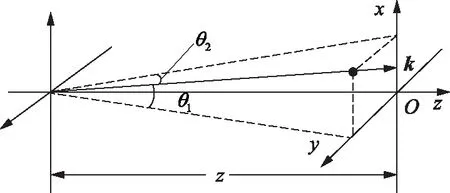
图1 沿方向角(θ1,θ2)传播的平面波
在傍轴近似下,中心在(x0,y0,-z0)的发散球面波和中心在(x0,y0,z0)的会聚球面波,在z=0波前平面上的相位分布φ+(x,y)和φ-(x,y)分别为[1]
(2)
式(1)和式(2)中,k=2π/λ表示波矢的大小。
2 全息记录与再现
如图2所示,一束正入射的单色平面参考光波,与一束球面物光波相干叠加,在z=0平面上形成干涉条纹。将记录介质放在该平面位置进行曝光,把干涉条纹拍摄下来,然后进行线性冲洗,即得到一张全息图。参考光波在z=0平面上的复振幅分布(即波前函数)为
(3)

图2 全息记录
在傍轴近似下,中心在(x0,0,-z0)的球面物光波的波前函数为
(4)
为方便计算,已设eikz0=1。二者相干叠加形成的干涉场强度分布为
(5)
(6)
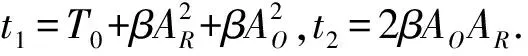
(7)
该衍射场一般是很复杂的。下面我们采用波前相因子判断法,就几种不同照明光波情形,详细分析全息图衍射场中物光波前的再现情况。
3 不同平面光波照明时全息图的衍射场分析
3.1 改变入射光波长

(8)
这与全息记录时参考光的波前函数相同。将上式代入式(7),并整理可将全息图的衍射场解析为
(9)
显然上式第一项只包含照明光波的信息,称之为0级衍射波。与式(4)中物光波的相因子比较可见,式(9)中第二项和第三项分别包含了物光波前及物光共轭波前,称之为+1级衍射波和-1级衍射波。由于照明光的波长与记录参考光的波长不等,即λ′≠λ,此时分析全息图的衍射场时,要以λ′为标准进行波前函数各项相因子的分析。为方便计,设
(10)
则+1级衍射波和-1级衍射波的相位分布φ+(x,y)和φ-(x,y)可改写为
(11)
可见,+1级衍射波为中心位于(x0,0,-z1)的一列发散球面波,-1级衍射波为中心位于(x0,0,z1)的一列会聚球面波,横向放大率V+=V-=1。即在全息图左侧成一等大的虚像,虚像位置相对于原记录物点有一个纵向的位移,在全息图右侧对称位置处成一等大的实像,如图3所示。这一特点使得我们可以采用不同波长的光,如红外光、紫外光甚至X射线记录全息图,而用可见光照射再现物光波前。

图3 改变照明正入射平面波波长时的成像图
3.2 改变入射光波的方向
如图4所示,当平面光波以θ角照明全息图时,其波前函数为
(12)
将上式代入式(7),并整理可将全息图的衍射场解析为
(13)
经整理,上式中第二项+1级衍射波和第三项-1级衍射波的相位分布φ+(x,y)和φ-(x,y)可表示为
(14)
其中,C1是与波前场点无关的常数。可见,+1级衍射波为中心位于[(x0-z0sinθ),0,-z0]的一列发散球面波,-1级衍射波为中心位于[(x0-z0sinθ),0,z0]的一列会聚球面波。即在全息图左侧成一虚像,虚像位置相对于原记录物点有一个横向的位移,在全息图右侧对称位置处成一实像。由于横向位移Δx=(x0-z0sinθ)-x0=-z0sinθ,与x0无关,所以横向放大率V+=V-=1,即所成虚像和实像与原物大小相等。如图4所示。这一特点使得我们可以通过改变照明光的传播方向,而实现再现像位置的调整。
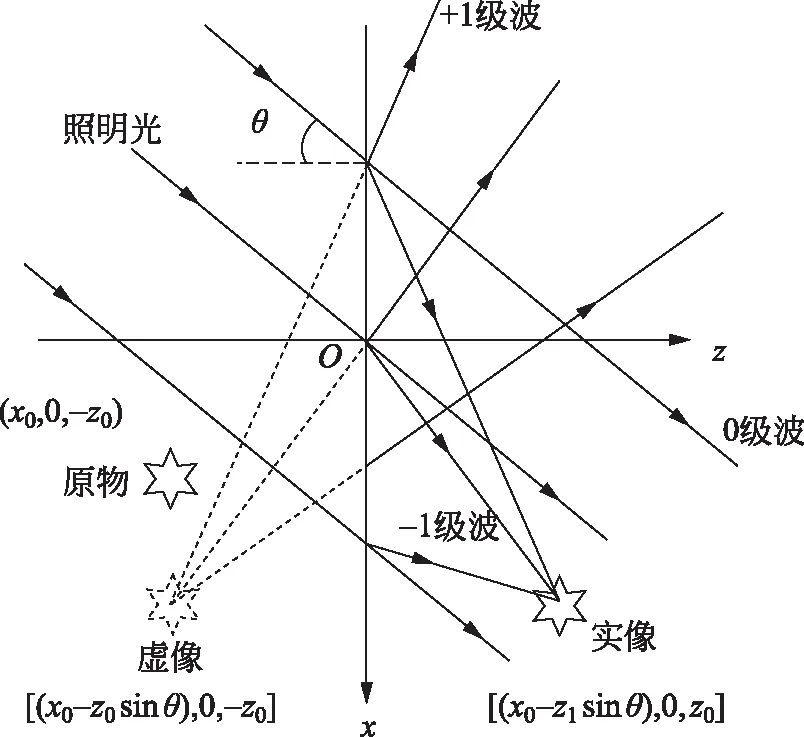
图4 斜入射平面波照明时的成像图
4 不同球面光波照明时全息图的衍射场分析
4.1 发散球面波作为照明光波
设照明光波为中心在(0,0,-z′)的发散球面波,满足傍轴条件时,此球面波的波前函数为
(15)
为方便计,我们已设exp(ikz′)=1。将上式代入式(7),并整理可将全息图的衍射场解析为
(16)
显然,上式中第一项的相因子与照明光波相同。下面我们主要对式中第二项+1级衍射波和第三项-1级衍射波的相因子加以分析。设+1级衍射波的相位分布为φ+(x,y),经推导可得
(17)
其中,C2是与波前场点无关的常数;z2满足下式
(18)
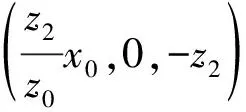
设-1级衍射波的相位分布为φ-(x,y),经推导可得
(19)
其中,C3为与波前平面上场点无关的常数;z3满足下式
(20)
(21)
考虑到z0与z′的大小关系,其成像可以分为以下两种情况:
(1) 当z0>z′时,根据式(20),有z3<0,则-1级衍射波为一列发散的球面波,即在全息图左侧形成一个虚像。由于|z3|可以大于、等于或小于z0,从而|V-|可以有大于、等于或小于1共3种不同的情况。即该虚像与原物体相比可能放大、可能缩小、亦可能等大。成放大虚像的情形如图5(a)所示。

图5 发散球面波照明的全息图(a) z0>z′; (b) z0 (2) 当z0 设照明光波为中心在(0,0,z′)的会聚球面波,满足傍轴条件时,此球面波的波前函数为 (22) 为方便计,我们已设exp(-ikz′)=1。将上式代入式(7),并整理可将全息图的衍射场解析为 (23) (1) 当z0>z′时,有z3<0,+1级衍射波为一列会聚的球面波。在全息图右侧形成一个实像。由于|z3|可以大于、等于或小于z0,从而|V+|可以有大于、等于或小于1共3种不同的情况。即该实像与原物相比可能放大、可能缩小、亦可能等大。成放大实像的情形如图6(a)所示。 图6 会聚球面波照明的全息图(a) z0>z′; (b) z0 (2) 当z0 我们采用波前相因子判断法对不同照明条件下全息图的衍射场进行了详细分析。结果表明,采用单色平面光波照明全息图时,所成虚像和实像关于全息图对称,且与原物大小相同。改变入射光的波长或传播方向,成像位置会有相应改变。采用单色球面光波照明全息图时,所成的两个像关于全息图不对称,且所成像的横向放大率存在大于、小于和等于1共3种可能性。全息成像的这些特点,在应用中具有实际意义。比如采用不同波长的光,如红外光、紫外光甚至X射线记录的全息图,均可以用可见光照射而再现物光波前;采用球面波照明全息图时可以将所成像进行放大或缩小;通过调整相应参量,可以实现成像位置的调整,等等。4.2 会聚球面波作为照明光波
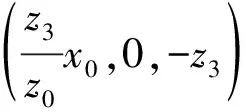


5 结论
