基于大数据分析思路的油滴实验数据处理方法

亓东林 鲍祎楠 张师平 裴艺丽 王荣明 吴 平

(北京科技大学 1计算机与通信工程学院， 2数理学院， 3自然科学实验中心，北京 100083)

密立根油滴实验是美国物理学家密立根(R.A.Millikan)于1909年完成的测量电子基本电荷的实验，密立根也因此于1923年获得诺贝尔物理学奖。在该实验中，密立根巧妙地运用了带电油滴在电场和重力场中的运动方程测量出油滴所带的微量电荷，并发现所有油滴所带的电量均是某一最小电荷的整数倍。目前，密立根油滴实验也是众多高校大学物理实验课程中为本科生开设的重要实验之一。

随着显微CCD的引入，密立根油滴实验在实验测量上变得更为方便，但其数据处理仍是很多专家学者关注的环节[1]。目前，文献所见的密立根油滴实验的数据处理方法主要有验证法[2]、作图法[3]、差值法[4]、最小正整数法[5]、对数法[6]、欧几里得算法[7]等等。其中，验证法和作图法已被广泛应用于教学中[2]。这两种方法都可以从不同程度上提高实验数据处理的精度，但其是基于已知元电荷公认值的基础上进行的数据处理，使得学生在数据处理过程中更倾向于求证，而不是探索求解元电荷的过程。

相比较而言，差值法和最小正整数法是在未知元电荷公认值的情况下进行数据处理，在这些方法中探索求解的思想更为明显。但差值法数据处理的结果容易与公认值产生较大的偏差[1]。最小正整数法依赖于实验测得的最小电荷量qmin的准确性，若最小电荷量与电子电荷的公认值的整数倍差别较大，则会带来较大的误差，并且学生在进行数据处理的过程中可能会根据电子电荷的公认值去选择合适的qmin以求获得较精确的结果，而增加人为的因素。

根据“所有测得的油滴电荷在误差不大的情况下是元电荷的整数倍”这一思路，本文用“对多个测量数据求最大公约数”的数据处理思想探索出一种基于大数据处理思路的基本电荷电量求解方法。

1 原理

假设在密立根油滴实验中测出n个油滴的电量，其实验测量数据分别为q1、q2、q3、…、qn。

取任意两个数据的比值为φij

φij=qi/qj

(1)

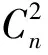
设正整数N为实验测得的油滴带的最大电荷数，将1/N～N/1范围内的所有正整数比记为bkm,即

bkm=k/m

(2)

其中,k，m为下标，且均为1～N的整数，k和m可以是相同整数，也可以是不同整数。

依次取φij中的每个数据与整数比bkm逐个进行比较，φij中每个数据均可在bkm中找到一个与之最为相近的值作为该数据的对应值，即认为两者相等。

由于老年患者各项器官机能均存在不同程度的衰老,再加上伴有一种或多种基础疾病,且骨科手术创伤较大,同时术后精神障碍与手术麻醉方案存在密切的关系,若患者未接受有效安全的麻醉处理,则会导致老年患者术后出现短期认知功能障碍。因此,有效的麻醉方案对手术治疗的老年骨科患者是非常重要的[1-5]。本次研究对象选择我院在2016年8月~2017年9月接诊治疗的60例行手术治疗的老年骨科患者,分析全身麻醉和硬膜外麻醉对老年骨科患者术后短期认知功能的影响效果,通过本组研究结果显示,实验组患者术后短期功能障碍发生率明显低于参照组患者,组间差异明显,P<0.05,存在统计学意义。

假设

φij=qi/qj=bkm=k/m

(3)

从而有

例如

利用以上方法，我们得到从q1到qn的所有数据两两相比的比对情况，即ei k和ej m。对所有的ei k和ej m从小到大排序，将相差在0.1%内的数据作为一组，从而得到多组数据。统计每组数据的数据个数，元电荷值应在数据个数最多的那组数据附近。将这组数据分别记为e1、e2，…el。对其求平均值，即可得到元电荷的实验值，如公式(6)所示

(6)

2 数据处理

根据以上理论，我们对密立根油滴实验的部分相关文献中所出现的数据进行了数据处理，其中原始数据如表1所示。

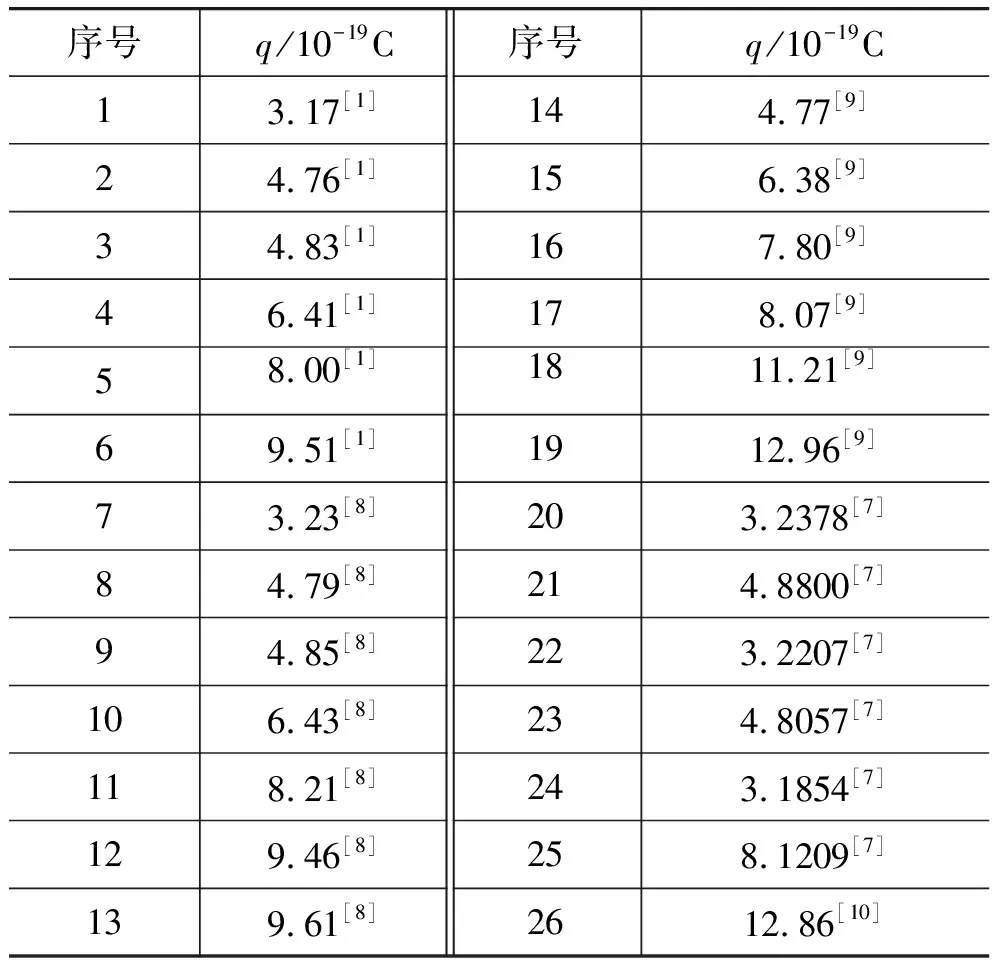
表1 密立根油滴实验部分文献中出现数据的列表

注： 数据精度不同是因为上述数据来源于不同的文献，原有文献的数据精度不同，本文中的计算结果与上述数据中有效位数最少的数据保持一致。

将以上数据代入式(1)～(6)，并将计算结果绘制在图1中。

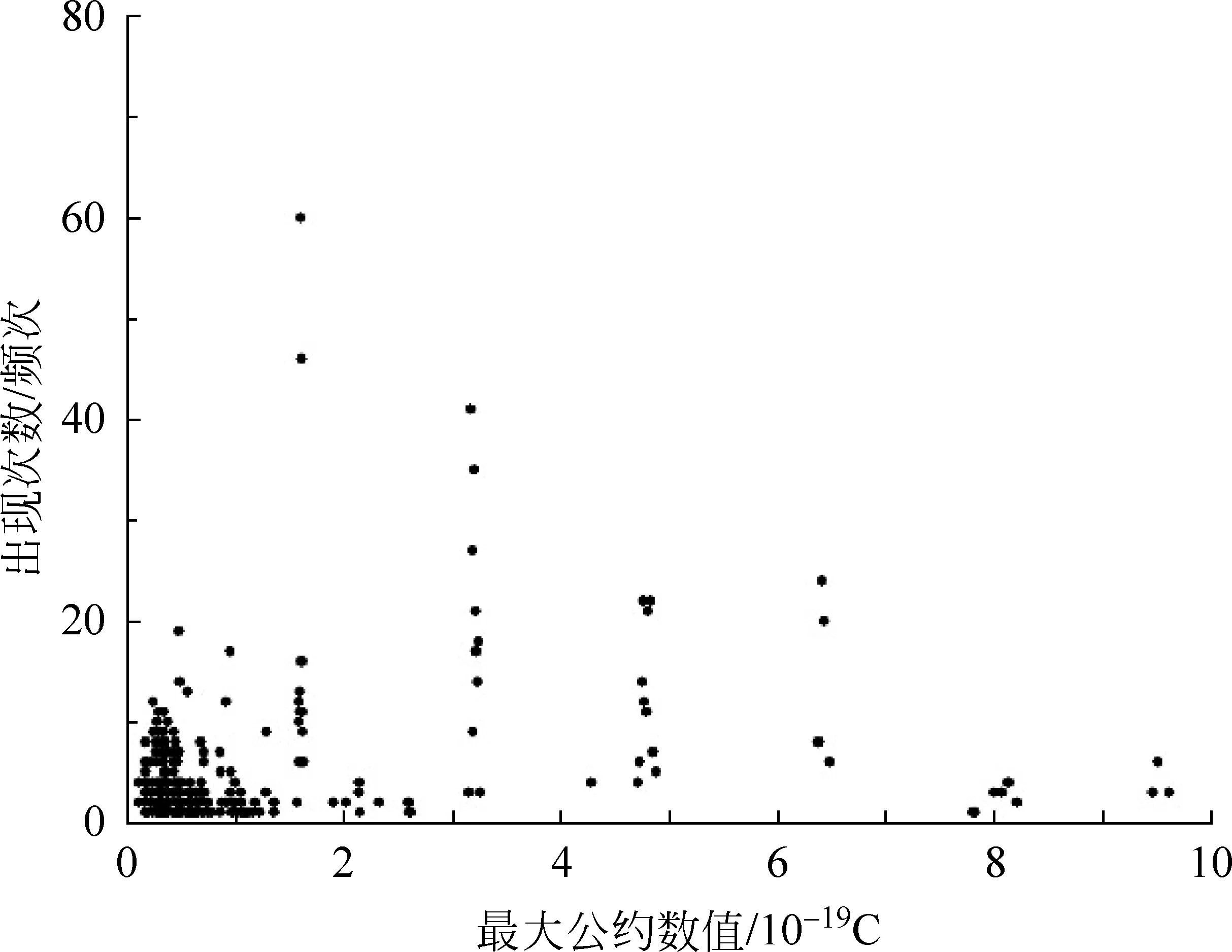
图1 文献数据计算所得最大公约数值的频数分布图

频次最大的数据的横坐标即为元电荷的值，此时为1.60×10-19C，与元电荷的公认值1.602×10-19C相比较，其相对误差为0.025%。

3 计算机辅助计算

3.1 对文献中的数据进行计算机辅助计算

在上一部分我们对文献中出现的39组实验数据进行了处理，任意两两比对后共得到了741组数据，因此很难通过手算进行数据处理。为此，我们利用计算机进行了辅助处理，流程图如图2所示。

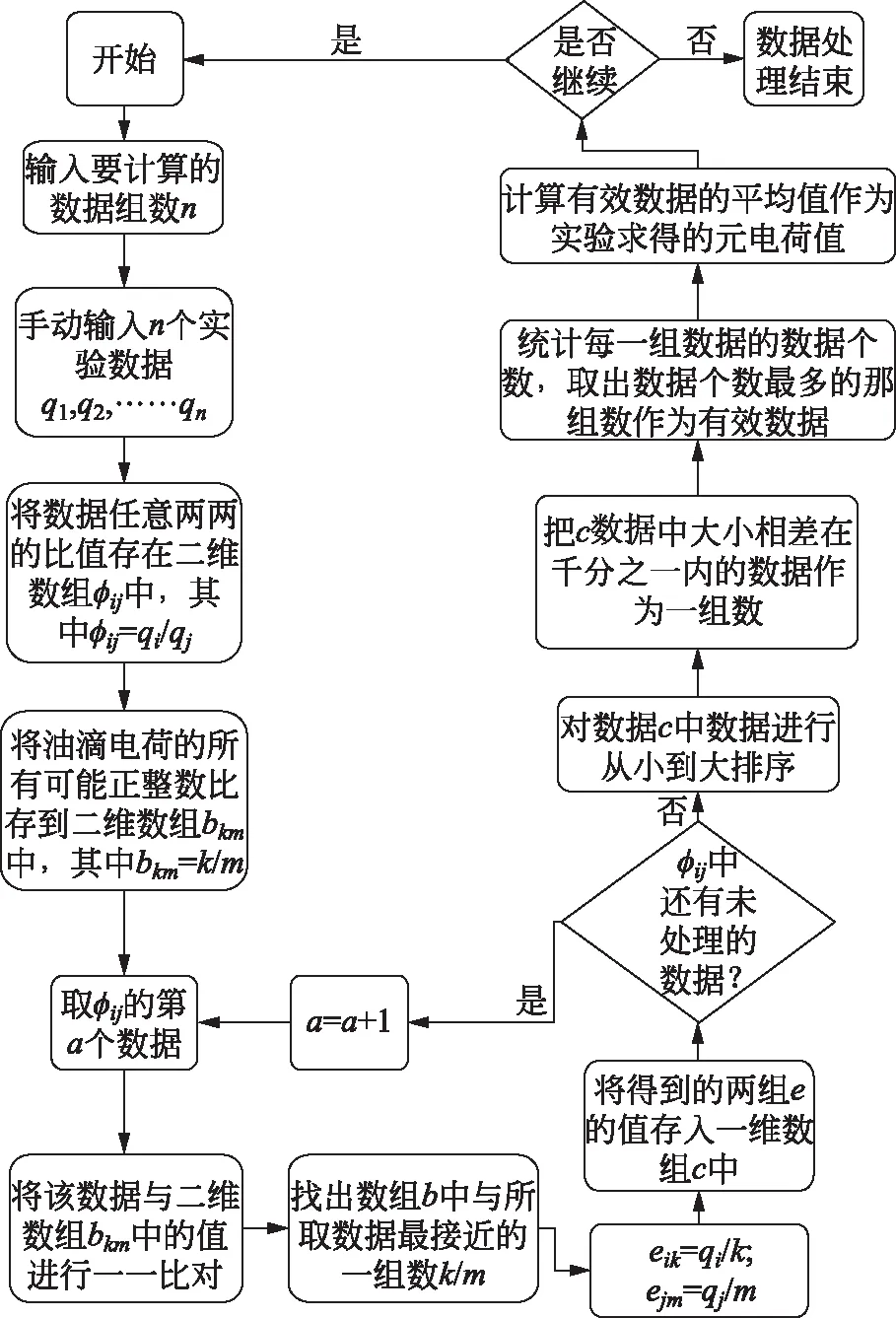
图2 计算机辅助计算流程图

我们重新对部分文献中的数据分别进行了计算机辅助计算，计算结果如表2所示。

与元电荷公认值1.602×10-19C比较，计算所得的相对误差如表2中所示。可以看出，与所列文献数据处理方法相比，采用本文方法处理得到的实验数据误差更小。

3.2 数据量对处理结果的影响

为了探究采用本文讨论的计算方法在不同数据量时对数据处理效果的影响，我们从2016—2017学年大学物理实验“电子电荷e值的测定”实验报告中提取了我校2015级本科生的全部原始实验数据，从中选取了实验报告得分大于平均分的上千个学生的实验数据(鉴于篇幅有限，不在此处一一列举)并进行计算。

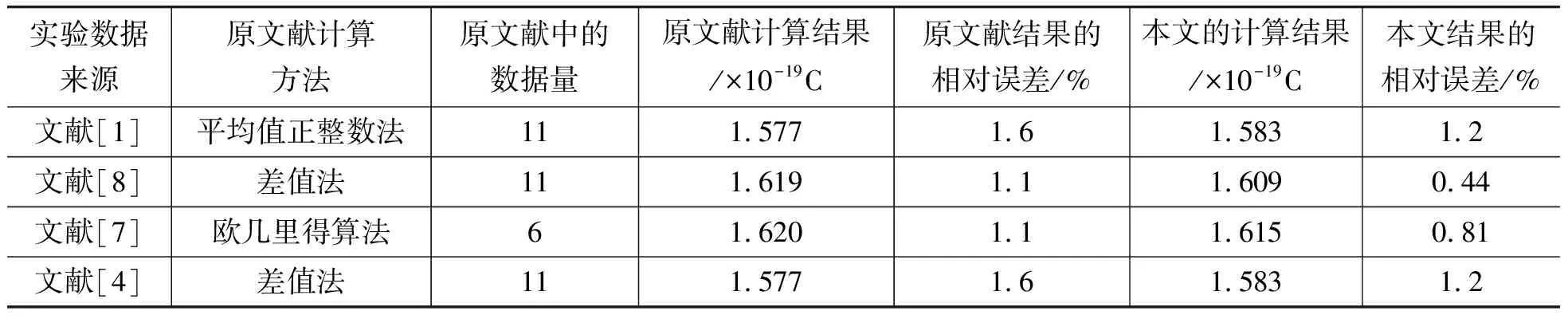
表2 部分文献数据处理结果与本文数据处理方法结果比较表

在这些数据中，我们分别随机选取了以10个数据为一组合计6组；以100个数据为一组合计6组；以500个数据为一组合计6组的3组样本。按照本文的数据处理方法进行数据处理，并求出了这3组样本的标准差来表示该处理结果的离散程度，结果如图3所示，图中的误差棒即表示该数据的离散程度。其中，6组10个数据的实验结果平均值为1.80×10-19C，标准差为1.8×10-19；6组100个数据的实验结果平均值为1.62×10-19C，标准差为0.03×10-19；6组500个数据的实验结果平均值为1.62×10-19C，此时标准差很小，甚至低于0.005×10-19。从图3中还可以看出，在一定范围内，样本数据量越大，得到的计算结果离散程度越小，结果的可信度越高。在数据处理中我们还发现，当数据量较少，如仅有10个数据，会出现所有实验数据均是元电荷的2或3倍甚至其他倍数的偶然情况，此时数据处理结果可能在3.2×10-19C或4.8×10-19C附近甚至更大的元电荷倍数值附近。当数据量较大时，则不会出现上述问题，这也从一定程度上体现出本文算法在数据量较大时的优势。

图3 由学生数据计算所得最大公约数值的频数分布图

4 结语

本文提出了一种最大概率比值法处理密立根油滴实验中的油滴电量数据，期望通过使用大数据处理的思想寻求一种使用优化后的最大公约数法处理密立根油滴实验数据的数据处理方法。该方法在不需要使用基本元电荷的公认值的情况下，可以计算出元电荷量，而且尽量避免了人为因素对数据处理过程中的干扰。同时，在一定范围内，使用该方法处理的数据量越大，越容易得到更为精确的数据处理结果。