侧面俯视时盛满水的碗中斜插筷子的虚像位置研究

(南京晓庄学院电子工程学院,江苏 南京 211171)

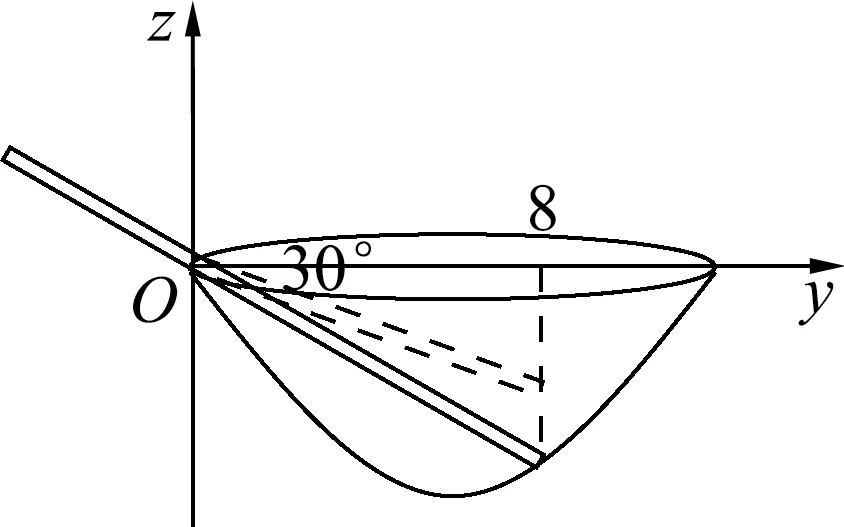
图1 侧面俯视时盛满水的碗中筷子的虚像

众所周知,从侧面俯视盛满水的碗中的斜插筷子时,会看到水中的筷子自水面处向上偏折,且视角(目光与水面法线即竖直方向的夹角)越大偏折越厉害,见图1.设筷子本身与水平方向的夹角为30°,碗里的筷子部分在水平方向的投影长度为8cm.但却少有人知道筷子虚像的准确位置以及虚像仍然呈现直线段形状的根本原因,更少有人知道筷子的虚像实际上还会向观察者这边偏折.本文将利用已有的光学知识计算出水中筷子虚像的准确位置,并运用MATLAB软件作出虚像的三维图像并加以分析.

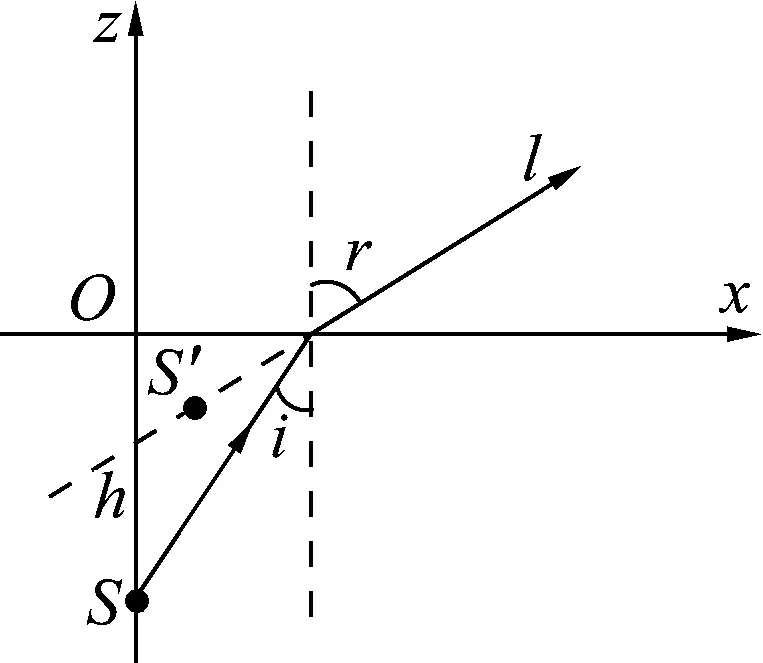
图2 来自水中物点的光线的折射

图2显示的是来自水下h深度的物点S的某条光线l,其入射角为i,折射角即人眼视角为r,像点S′就在折射光线的反向延长线上,且在物点S的右上方.[1]姚启钧《光学教程》(第4版)[2]给出像点S′的坐标如下

x=h(n2-1)tan3i，

(1)

(2)

其中水的折射率n=4/3.由于这里的物点S来自图1中水面以下的筷子,因此可将物点的深度h表示成

(3)

将式(3)分别代入式(1)、(2)并考虑到n=4/3后,即得像点S′的空间轨迹方程

(4)

(5)

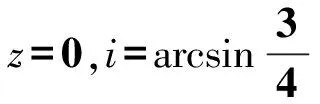
设视角r=30°和60°,则由折射定律sini=sinr/n可算出i=22.0°和40.5°,继而得到tani=0.405和0.854.将tani值代入式(4)、(5)便得在这两个视角下筷子虚像的位置

当r=30°时，

x=0.030y,z=-0.353y，

当r=60°时，

x=0.280y,z=-0.123y，

其中y∈[0,8] cm.

运用MATLAB软件可作出水中筷子实物及其虚像的三维图像,见图3和图4.当然,我们实际看到的只有虚像.从图中可见,或更精确地从上面式子算得,在30°和60°视角下筷子的虚像与右边“网格墙”的交点坐标分别为(0.24,8,-2.82)和(2.24,8,-0.98),而筷子实物与右边“网格墙”的交点坐标则是(0,8,-4.62).显然60°视角下筷子的

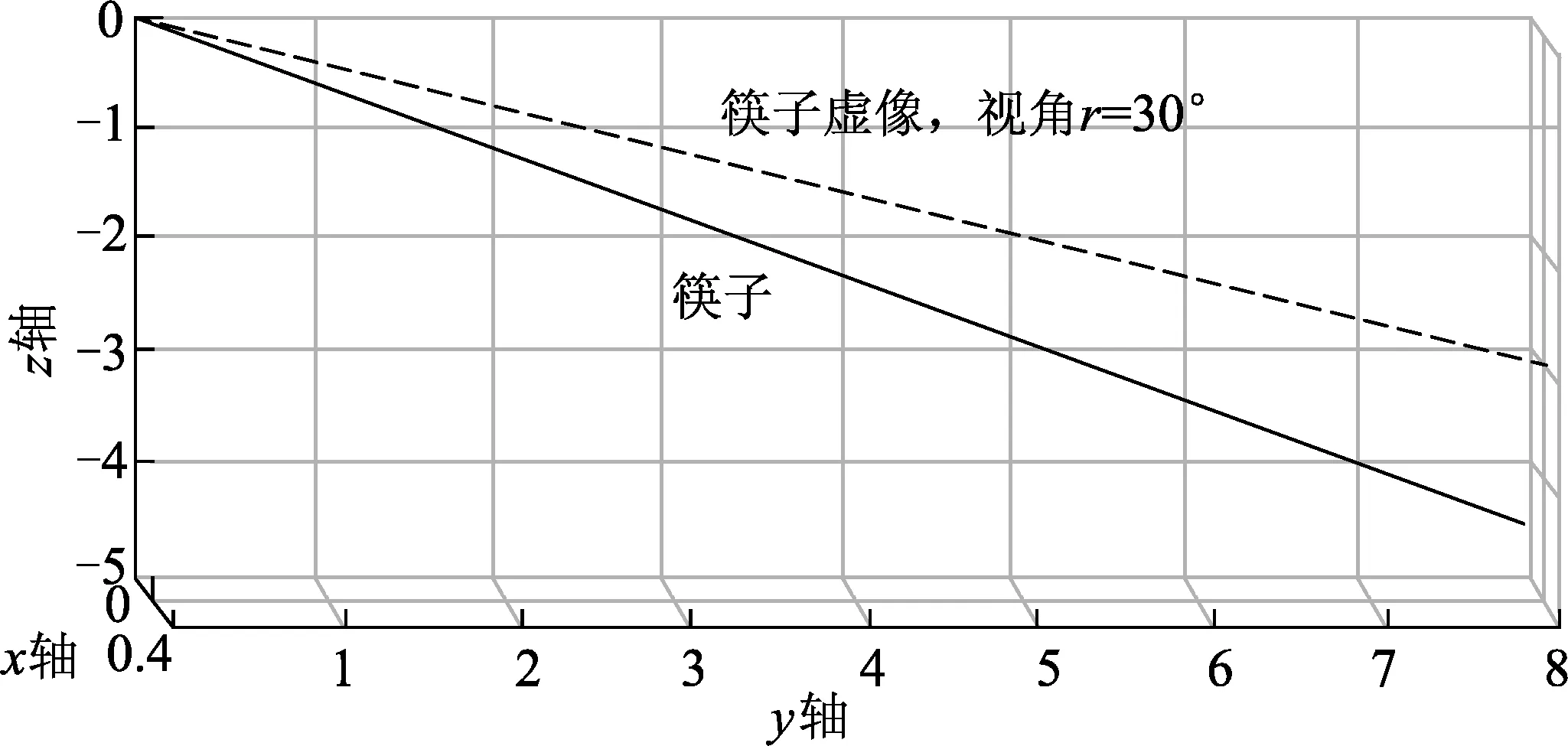
图3 碗内水中的筷子实物与其在30°视角下的虚像

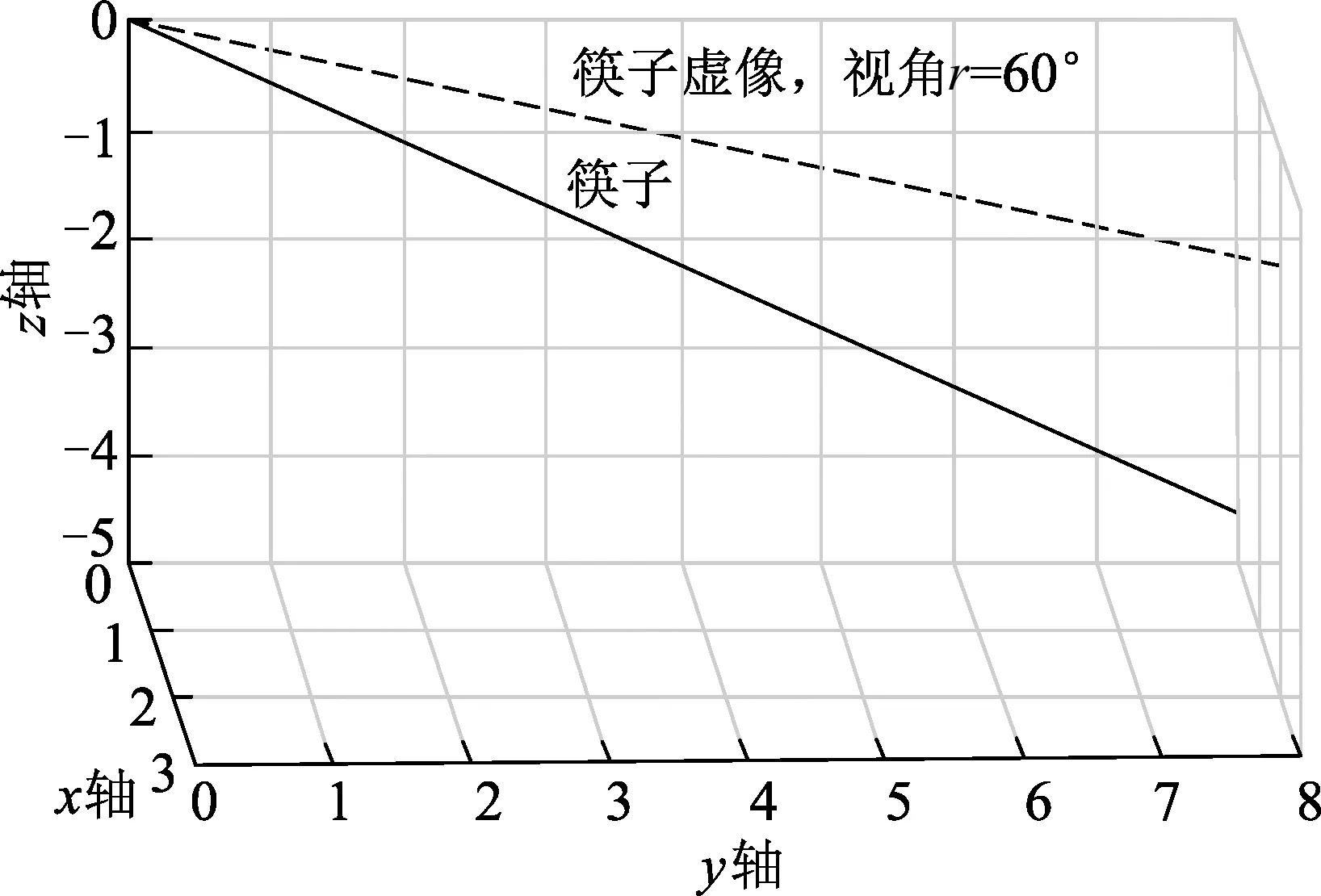
图4 碗内水中的筷子实物与其在60°视角下的虚像

虚像相对于实物要向上(z轴正方向)、向外(x轴正方向)偏折许多.不过,由于我们看到的碗底也是虚像,它和筷子端的虚像同步移动,以及我们从侧面观察的视觉缘故,我们虽然能明显地看到筷子向上偏折,却不易看到筷子向我们眼睛这边偏折.除非你把筷子换成标有刻度及文字的尺子,并用近视的裸眼去仔细观察.

需要说明的是,虚像的位置是随视角变化的,30°视角和60°视角下筷子虚像的位置是不同的,因此这两个虚像宜分图画出,如图3和图4,代表着两个不同的视角.事实上,笔者在作图3、4时已考虑了此视角因素.另外,严格地讲,本文计算的实际是筷子的子午虚像．[2,3]若将图3、4中筷子的子午虚像(虚线)沿着目光的方向向O-yz平面投影,即得筷子的另一理论虚像——弧矢虚像．显然这两个虚像总是重叠在一起的,我们的目光只能聚焦于前面的子午虚像,永远无法透视看到后面筷子的弧矢像,因此这里用筷子的子午虚像作为筷子虚像是准确的.