基于正交实验的履带机器人张紧力优化

王亚翔 张俊俊

(西南科技大学特殊环境机器人技术四川省重点实验室 四川绵阳 621010)

履带是履带机器人中的重要部件之一。其功能是保证机器人在无路地面上的通过性，降低车辆的行驶阻力。而履带机器人的通过稳定性可以通过履带张紧力来评估，履带的张紧力对于履带行驶系统的性能有深刻影响。张紧力过大，履带刚度太大，起不到缓冲作用，会增加履带和底盘部件摩擦，能耗严重，并有断带危险；张紧力过小，使得履带松弛，容易脱带、耙齿，造成履带失效，车辆瘫痪[1-4]。为了使机器人更好地适应环境、提高机器人在遥操作过程中的稳定性和高效性，有必要对其在典型环境中工作时张紧力的变化进行研究，以提高自适应履带机器人的综合性能，方便实际应用中设计合理的机器人结构并明确对机器人的操作和控制[5]，因此张紧力的计算和优化成为研究的重点。

国内外许多学者对履带张紧力进行了分析，Park等[6]将低速履带环看成柔性带，通过建立履带的数学模型分析履带车辆的行驶性能，Wong等[7]以NTVPM模型预测小型、轻型履带车辆在可变形地形上的越野性能。刘汉光等[8]研究了履带液压挖掘机行走装置的合理预张紧力。马兴国等[9]通过建立数学模型得到了履带系统各部位的张紧力以及地面对负重轮法向力的计算公式。本文根据自行设计的自适应履带式机器人地盘为模型，通过理论分析研究履带机器人张紧力分布，得出了主动轮附近张紧力计算公式，并通过Recurdyn软件的Track(LM)工具建立移动平台的虚拟样机模型验证了计算公式的可行性。同时通过正交实验得出履带机器人设计中的主要参数对张紧力的影响显著性，为履带式机器人设计和优化提供依据。

1 履带机器人结构

本文设计的履带机器人机构如图1所示，其中为单边履带系统，包括了主动轮1、诱导轮3、负重轮10、电机与减速器8、电源7和主控6，履带单边可以单独提供数据传输与控制，独立的电源与电机可以是履带单边独立完成行走任务。其中为了提高越障性能，前进方向处的负重轮处设计了被动自适应变形结构，包括了变形板4和负重轮10以及变形减震弹簧11。变形板在越障受力后被动变形，减小前角大小从而增加越障性能。

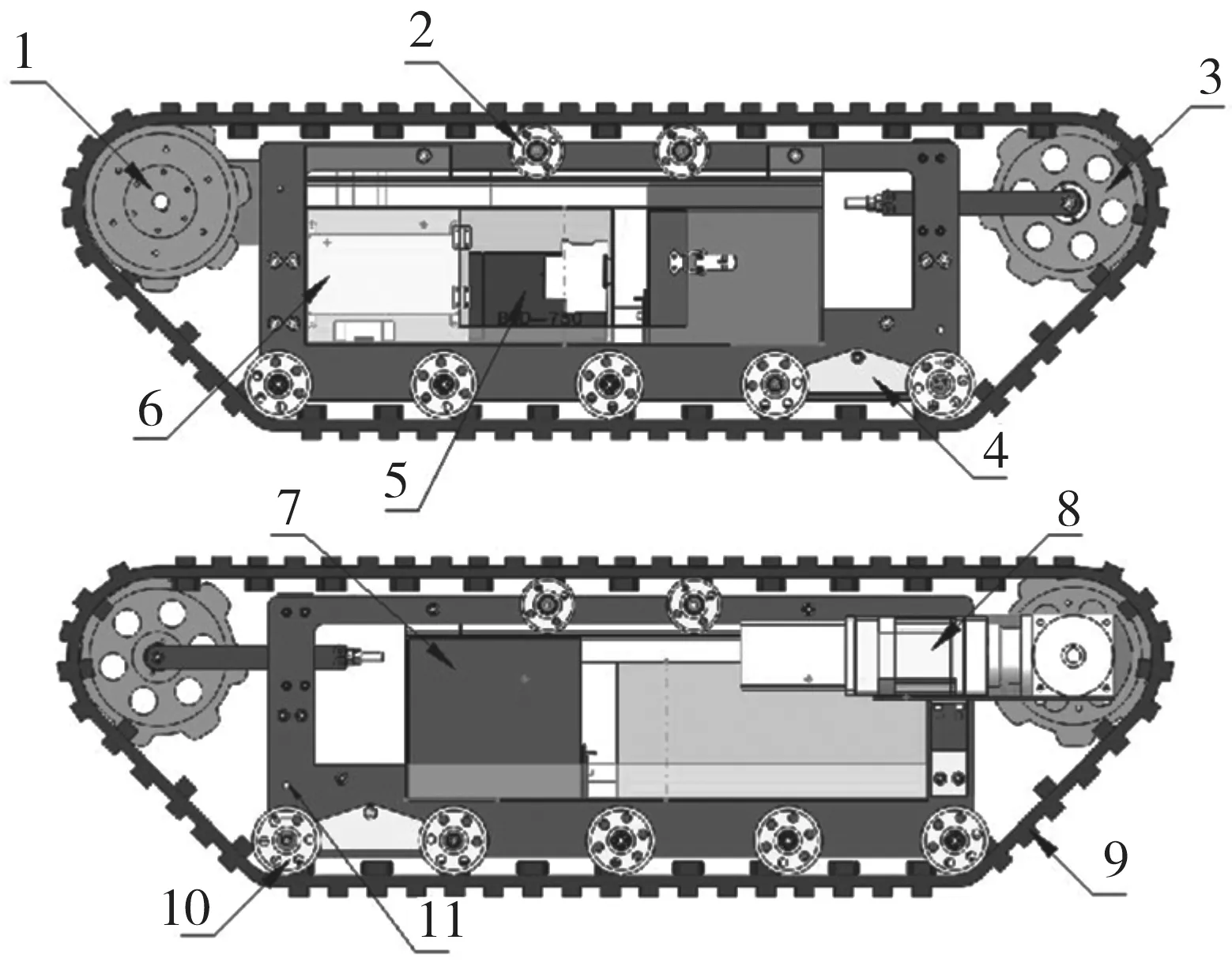
1.主动轮， 2.托带轮， 3.诱导轮， 4.变形板， 5.驱动器，
6.主控通信模块， 7.电池， 8.动力模块(电机与减速器)，
9.履带， 10.负重轮， 11.弹簧

图1履带机器人结构
Fig.1 Structure of tracked robot

2 履带系统力学分析

履带机器人的履带系统由主动轮、托带轮、诱导轮、负重轮组成，如图2所示。由于设计的履带机器人其托带轮与主动轮和诱导轮相切履带为直线，因此忽略主动轮和诱导轮之间的履带板的重力和振动以及托带轮的影响，分析时将履带系统分为主动轮、负重轮、诱导轮三部分，则可以认为Td1≈Tc2。

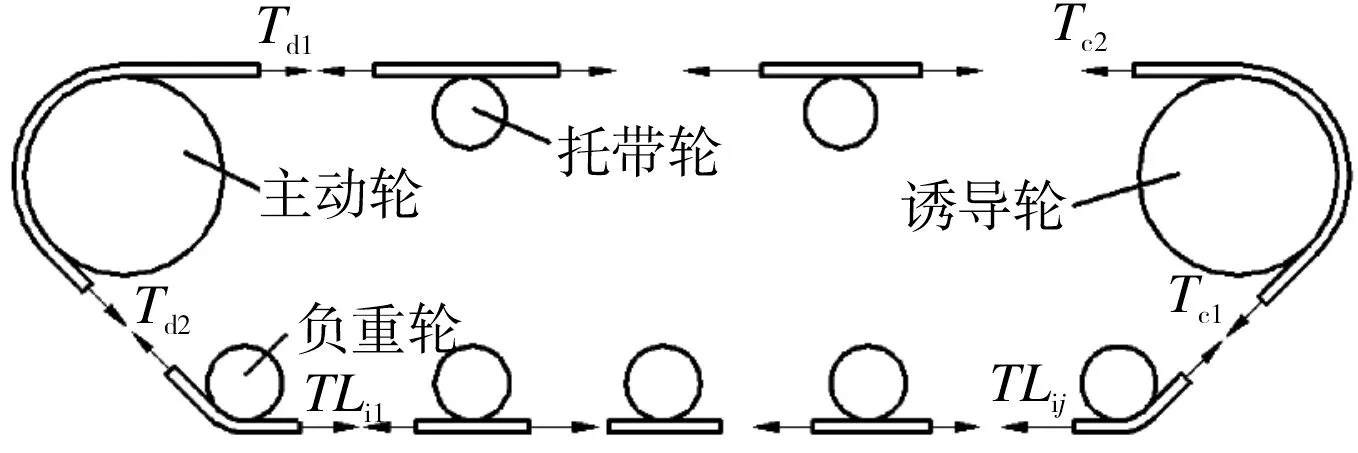
图2 履带张紧力系统模型Fig.2 Mechanical model for tension system

2.1 轮系张紧力

取主动轮为隔离体，得到主动轮受力如图3(a)所示，可以得出主动轮处张紧力为：

(1)

式中：M为主动轮转矩；Td1,Td2为主动轮处松边张紧力和主动轮处紧边张紧力。

图3 主从轮系受力分析Fig.3 Mechanical model for driving wheel and induction wheel

取诱导轮为隔离体，得到诱导轮轮受力如图3(b)所示，可以得出诱导轮处张紧力动力学方程为：

(2)

式中：mc为从动轮质量；Fct为履带预张紧力，Fc为诱导轮周围履带旋转的离心合力；γ为离心合力与水平夹角；Tc1，Tc2为诱导轮处履带受张紧力松边、诱导轮处履带受张紧力紧边；α为履带机器人前角，Gc为诱导轮受到的重力；Jc为履带诱导轮转动惯量；Rc为诱导轮半径；ωc为履带机器人匀速前进诱导轮角速度；Fcn为诱导轮y方向支撑力；ρ为履带单位质量。

取履带负重轮系为隔离，不变形负重轮系受力如图4(a)所示，变形负重轮系受力如图4(b)所示。

图4 负重轮系分析Fig.4 Mechanical model for load wheel

得出不变形负重轮处履带张紧力动力学方程为：

(3)

(4)

被动自适应变形处的负重轮履带张紧力动力学方程为：

(5)

(6)

式中：ml为负重轮质量；TLi1,TLi2为各负重轮处张紧力；β为履带后角；α为履带前角；RL为负重轮半径；Jl为负重轮转动惯量；fLi为各负重轮与履带间的摩擦力；FLin，FLit为负重轮y，x方向支撑力；ωLi为各负重轮角速度；Gl为负重轮受到的重力；NLi为各负重轮与履带间的法线接触力，u·NLi=fLi；u为履带与负重轮间摩擦系数，u1为履带与负重轮间滚动摩擦系数。

综合式(1)-式(6)可以得出主动轮处两端的张紧力分别为：

(7)

对于变形负重轮处的变形板有：

(8)

其中：

(9)

式中：W为履带机器人对在变形板上的均布压力；mB为变形板质量；ml为负重轮质量；φ为变形板斜边与法线夹角；LB为变形板边长；TB为变形板受到的转矩；k为弹簧刚度；θB为变形板微变形后变化角度。

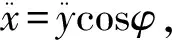
(10)

从式中可以看出，自适应履带主动轮附近张紧力与主动轮、从动轮半径、质量、自适应负重轮处弹簧刚度、转动惯量、前角和后角角度相关。

2.2 公式计算与仿真对比

为了验证张紧力推导公式的可靠性，在多体动力学软件Recurdyn中使用Track模块建立了被动自适应履带机器人的动力学模型，当选用表1参数进行理论计算和仿真实验时(履带预张紧力以总质量百分比为单位)，得到的仿真曲线对比图如图5所示。通过文中推导公式计算张紧力Td1平均值为1 134.3 N，仿真计算张紧力Td1平均值为1 092.1 N，通过图5可以看出两个曲线变化规律相符合，因此公式准确性较好。

表1 仿真参数Table 1 Parameters of simulation

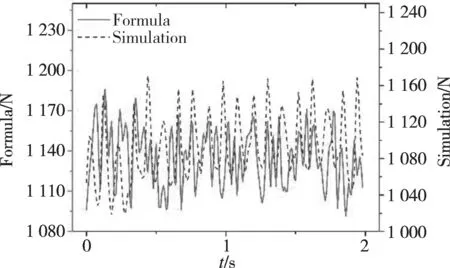
图5 张紧力Td1公式计算与仿真对比Fig.5 Comparison between calculation of tension force Td1 and that of simulation

3 基于正交实验的参数优化

从式(10)可以得出当机器人质量、尺寸参数确定时，改变其中任何一个设计参数都会引起对主动轮附近张紧力的影响。为了得出多个设计参数对运行过程中履带张紧力变化影响的显著性，本文将前角α、后角β、预紧力Fct、变形弹簧刚度k4个重要履带设计参数作为正交实验因素，每个因素选取4个水平，选取L(45)正交表进行实验，正交实验表如表2所示，16次正交实验得出由理论计算与仿真实验的张紧力均值变化图如图6所示。从表3和图6可以看出正交实验中理论公式计算的张紧力Td1的变化趋势与仿真相一致且计算得出的张紧力均值相近，因此可以进一步验证理论公式的有效性，同时在极差与方差分析中将会采用正交表中的仿真均值作为分析数据。根据表2数据得出的4因素方差分析结果如表3所示。可以根据表2的极差和表3的方差分析看出前角α、后角β、预紧力Fct对实验结果有显著性影响，其数值的改变会引起张紧力数值的显著性变化，其中预紧力Fct对实验结果影响极其显著。

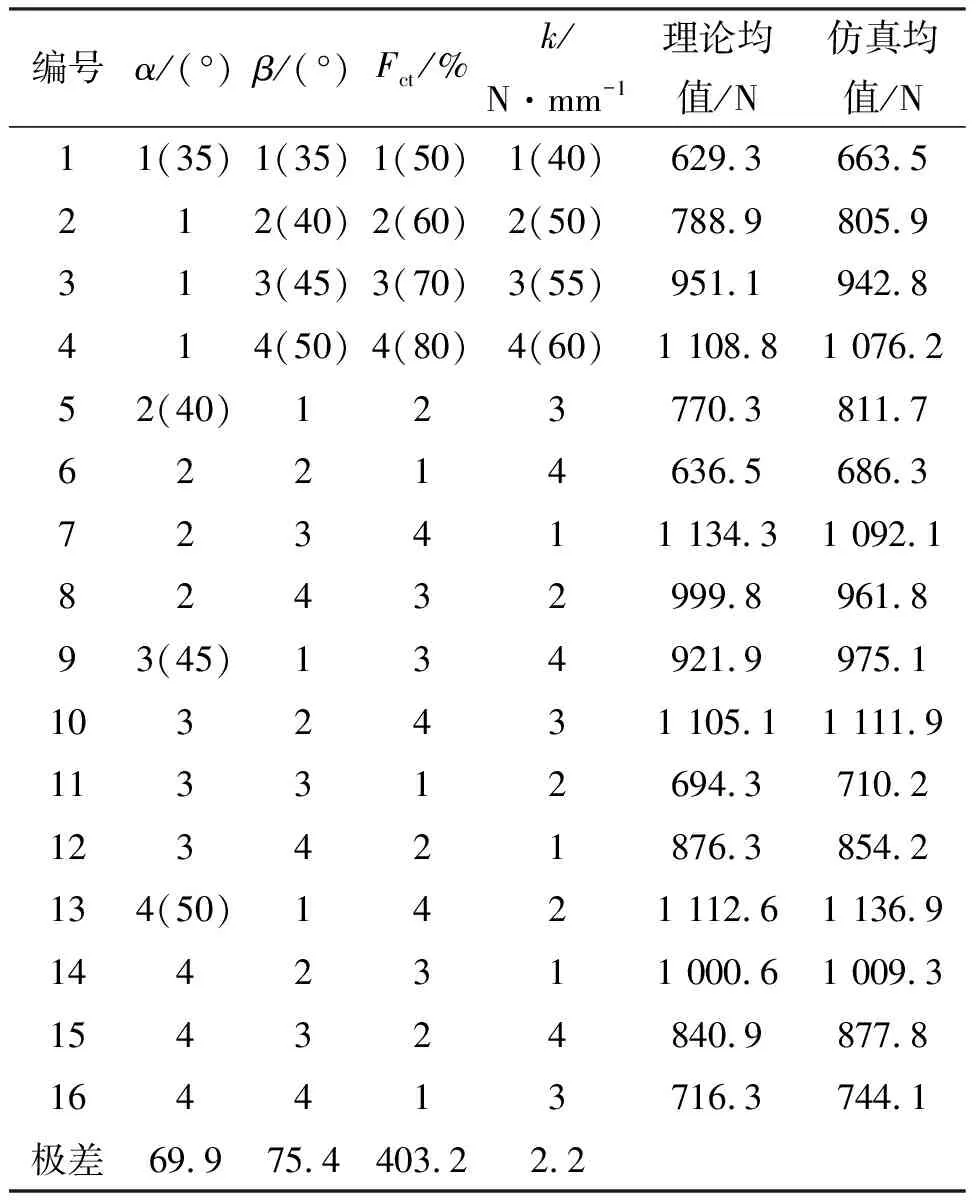
表2 正交实验设计Table 2 Orthogonal test design

图6 正交实验中张紧力变化Fig.6 The change of tension in orthogonal test

因素偏差平方和自由度方差FProb>Fα1.11e433 732.1490.621.56e-4β321.83107.314.120.028Fct3.62e531.21e515 850.198.5e-7k9.633.20.420.75误差e22.837.6总和3.73e515

通过利用正交实验中的数据在Recurdyn中建立了动力学模型，仿真得出了16次试验中履带机器人在法线方向的加速的变化，如图7所示。从表3和图7可以看出，履带整体尺寸确定时，前角α与后角β过小时，履带法线加速度及其均方差较大，稳定性较差；当前角α与后角β增大后，预紧力Fct的变化对其法线方向加速度的均方差影响较大；其中第11次实验中履带机器人的法线加速度和均方差最小，初始预张紧力为整体重力的50%，这时履带主动轮处张紧力均值为710.2 N，相比正交实验的其他实验中履带张紧力处于中间水平，可以同时综合脱带与减震的情况。

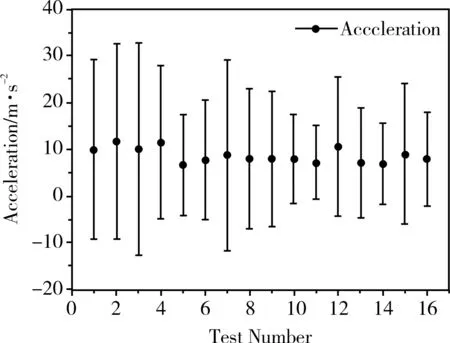
图7 履带机器人法线方向加速度变化Fig.7 Acceleration change of crawler robot in normal direction

4 结论

通过建立数学模型、理论分析、仿真以及正交实验，得出以下结论：(1)建立了被动自适应履带机器人负重轮、主动轮、诱导轮附近的履带张紧力数学模型，得到了被动自适应履带机器人张紧力的计算公式，并通过用公式计算得到的曲线与仿真结果相比较，计算公式与仿真实验得出的张紧力曲线变化趋势相符合，验证了论文建立的被动自适应履带张紧力公式的可行性。(2)通过建立正交实验，得到了被动自适应履带机器人多个结构参数对履带张紧力的影响显著性。得出了在多个结构参数同时影响的情况下，预紧力对自适应履带运行中张紧力影响显著性最大。并得到了履带机器人以前角45°、后角45°，预紧力为总重力的50%～60%时设计时，自适应履带机器人直线行走稳定性最优。