浅谈轮系传动比的辩证施教

侯杰茹

（天津职业技术师范大学机械工程学院 天津300222）

在生产实际中，轮系作为应用广泛的传动装置，用来在输入轴和输出轴之间传递运动和动力，以满足一定的功能要求。无论是分析已有轮系，还是设计新的轮系，都需要计算轮系的传动比。因此，在机械原理课程的教学过程中，轮系的传动比计算是轮系的重点教学内容，要求学生熟练掌握轮系传动比的计算方法。

根据运动特性和结构组成，轮系分为定轴轮系、周转轮系和混合轮系三大类，轮系的类型不同，其传动比的计算方法也各不相同，但是它们之间有一定的内在联系。其中，定轴轮系的传动比计算是基础，比较简单；周转轮系的传动比计算是在定轴轮系的基础上演化进行的，有一定的难度；而混合轮系的传动比计算是对两者加以综合进行的。

在教学过程中，笔者发现：学生在学习这部分内容时存在这样一些问题：对于定轴轮系的传动比计算，有一些学生认为较简单，对其不够重视，容易马虎大意，在计算时出现不应该出现的错误；在计算周转轮系的传动比时，因对其计算方法的本质理解不够深刻，有些概念比较模糊，不能熟练掌握，感到有一定的难度；而在计算混合轮系的传动比时，因前面的基础知识未能熟练掌握，在学习时感觉有一定困难，不能正确地进行计算，造成教学效果不理想。

要解决以上问题，教师在授课时需要辩证施教，讲清三种轮系传动比计算的关键和本质，提高学生对计算方法的认知水平，理清概念，进而熟练地掌握计算方法，提高教学效果。

重视定轴轮系传动比计算的基础

因为定轴轮系在工程实际中应用非常广泛，而且，定轴轮系的传动比计算是其他类型轮系的基础，因此，定轴轮系的传动比计算是轮系的重点教学内容之一，在教学时，需要告诉学生必须重视并熟练掌握它。

在计算轮系的传动比时，不仅要计算传动比的大小，还要确定首轮和末轮的转向关系。定轴轮系的传动比等于组成该轮系的各对啮合齿轮传动比的连乘积。其大小等于各对啮合齿轮中所有从动轮齿数的连乘积与所有主动轮齿数的连乘积之比。因此，在计算时，对轮系进行结构组成分析是关键。首先，明确首轮和末轮；其次，按传动路线分析从首轮至末轮轮系由几对齿轮组成，确定各对齿轮中的主动轮、从动轮；最后，再进行计算。在授课时，教师要告诉学生对机构进行结构组成分析是计算传动比的基础，针对轮系的机构简图，能熟练正确地确定定轴轮系的结构组成。

确定轮系首轮和末轮的转向关系对计算轮系的传动比很重要。学生在学习时，对其不够重视，出现一些不应该出现的错误，主要体现在对用齿数比前的“+”、“-”来表示首轮和末轮的转向关系的理解上。

在教学过程中，首先，教师要讲清，对于平面定轴轮系和首末两轮轴线平行的空间定轴轮系，为了在计算公式中能直观表明首轮和末轮的转向关系，规定在齿数比前加上“+”、“-”来表示首轮和末轮的转向关系。若轮系的首轮和末轮分别为1和K，则其传动比为：

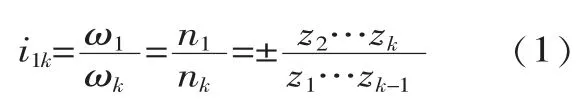
对平面定轴轮系，通常根据外啮合齿轮的对数m来判断，即先由（-1）m的 计 算 结 果 得 齿 数 比 前 的“+”、“-”，然后再根据“+”、“-”来判断首轮和末轮的转向关系。而对于首末两轮轴线平行的空间轮系，则用画箭头法先确定首轮和末轮的转向，然后在齿数比前加上相应的“+”、“-”来代表两轮的转向关系。

最后，教师要从辩证的角度，强调首轮和末轮的转向关系是由轮系的结构决定的，即是由轮系自身的内在因素决定的；明确这一点是非常重要的，是后面学习周转轮系的传动比计算的基础。

认清周转轮系传动比计算的本质，突破难点

周转轮系传动比的计算方法，对于学生来说既是需要掌握的重点内容又是难点内容。要求教师在授课时讲清计算方法的本质，使学生理清计算的基本思路和应注意的事项。

周转轮系与定轴轮系的根本差别在于周转轮系中有作定轴转动的系杆，它使得行星轮既自转又公转，因此，周转轮系的传动比就不能直接用定轴轮系传动比的求法来计算。但是，假如能使周转轮系中支承行星轮的系杆H固定不动，周转轮系便转化为一个假想的定轴轮系，就可以借用定轴轮系传动比的计算方法进行周转轮系传动比的计算，这就是计算周转轮系传动比的基本思路。

在教学过程中，对于将周转轮系转化为一个假想的定轴轮系（转化轮系），除了从给整个轮系加上一个-ωH的公共角速度的角度介绍之外，还可以从哲学对运动的辩证描述的角度进行介绍。在哲学范畴中，运动是绝对的，但我们观察物体的运动却有相对性，所选的参考体不同，那么物体相对于不同参考体的运动也不同。若取系杆H为参考体，当观察者站在系杆H的轴上观看轮系的运动时，对观察者来说系杆H固定不动，这时，行星轮相对于系杆H只作定轴转动，于是，周转轮系便转化为一个假想的定轴轮系。从这个角度对转化轮系进行介绍有助于清晰地理解计算过程中涉及的“+”、“-”。 根据上述原理，就可以得出周转轮系的转化机构传动比的一般公式。设周转轮系的两个中心轮分别为1和K，则其转化轮系的传动比为：

在学习过程中，学生感到对计算公式的理解有一定的难度，主要体现在对计算过程中涉及的两套“+”、“-”的理解上。因此教师在授课时，需要从辩证的角度讲清所涉及“+”、“-”的含义，认清两者的本质区别。

一方面，首先明确公式（2）中齿数比前的“±”号表明的是在转化轮系中齿轮1、K的转向之间的关系。若相对角速度ω1H、ωkH的方向相同，在齿数比前为“+”号，而转向相反则为“-”号，判断两者转向关系的方法与定轴轮系相同。在此，教师需要强调，转化轮系中齿轮1、K之间的转向关系，相当于观察者站在系杆H的轴上观看轮系的运动时，所看到的齿轮1、K的转向关系，是由轮系自身的结构这一内在因素决定的，明确了这一点，学生对齿数比前的“±”号就有了清晰的认识。

另一方面，公式（2）仅适用于齿轮1、K和系杆H的轴线平行或重合的周转轮系。对于差动轮系，在计算时需要表明轮系中齿轮1、K和系杆H之间的实际转向关系。在此，教师需要讲清，为了反映差动轮系中齿轮1、K和系杆H之间的实际转向关系，设定齿轮1、K和系杆H的绝对角速度ω1、ωk、ωH均为代数量，用其值的符号来表示转向关系，规定：对于绝对角速度已知的两构件，若两构件的转向相反，一个角速度取正值，另一个则取负值代入公式中；若两构件的转向相同，两角速度可皆取正值（或负值）代入公式中；所求出的第三个构件的角速度，其值的正、负则表明该构件与其他两个构件间的转向关系，符号相同的两者转向相同，符号不相同的则转向相反。需要强调的是，两主动构件的角速度是从外界输入的，其实际转向是根据使用情况人为指定的，即两主动构件的角速度值的正、负值是由外在因素决定的，这就是与前述的齿数比前“±”号的本质区别。

分清混合轮系，综合应用

混合轮系是由基本周转轮系和定轴轮系组成，或者由两个以上的周转轮系组成。对于混合轮系传动比的计算，既不能直接套用定轴轮系的公式，也不能直接套用周转轮系的公式。

计算混合轮系传动比的正确方法是首先正确地划分出各个基本轮系，分别计算各基本轮系的传动比，找出各个基本轮系之间的联系，然后联立求解。其中，最重要的一步是正确地划分出各个基本轮系。

学生在学习混合轮系传动比的计算时，感觉有一定困难，不能熟练地掌握计算方法。出现这一问题的主要根源在于学生对正确地划分出各个基本轮系不够重视，没有搞清划分轮系的顺序和步骤。因此，教师在授课时，首先，要强调正确地划分轮系的重要性，它是计算混合轮系传动比的基础，是正确解题的关键；其次，讲清划分轮系的正确顺序是一定要先划分出各个基本周转轮系，最后再找定轴轮系。

在划分单一的周转轮系时，首先找出行星轮。从结构上来说，行星轮是由作定轴转动的构件支承的齿轮，行星轮和支承它的构件组成活动铰链。接下来找出系杆，支承行星轮的构件就是系杆。（注意：有时系杆不一定是杆状！）最后找出中心轮，中心轮是直接与行星轮啮合且几何轴线与系杆的轴线重合的定轴齿轮。这一由行星轮、系杆、中心轮组成的轮系就是一个基本周转轮系。一般情况下，混合轮系中有几个系杆，就包含几个基本周转轮系。在上述过程中，根据结构特点找出行星轮、中心轮是正确地找出周转轮系的关键。

当把所有的基本周转轮系找出来之后，剩下的互相啮合的定轴齿轮就组成定轴轮系。正确地划分出各个基本轮系后，就可以按混合轮系传动比的计算方法进行计算了。

结论

综上所述，教师在轮系传动比计算的教学过程中，引入哲学的方法讲解难点和重点，学生感到概念清楚了，思路清晰了，有助于更好地掌握计算方法，普遍反映效果很好。比如，有学生说：“老师用哲学讲课，能引起学生的注意力，同时，也提高学生学习的兴趣。用哲学讲复杂的问题时，能给我一个清晰的思路，有恍然大悟的感觉。”因此，在教学过程中，教师要善于从辩证的角度进行教学，以便更好地激发学生的学习兴趣，进一步加强对学生分析问题和解决问题能力的培养，有效地提高教学效果。

[1]申永胜.机械原理教程[M].北京：清华大学出版社，2005.

[2]刘瑛，侯杰茹.机械设计基础[M].北京：中国电力出版社，2009.

[3]张春林.机械原理[M].北京：高等教育出版社，2006.

[4]张策.机械原理与机械设计[M].北京：机械工业出版社，2006.

[5]申永胜.机械原理辅导与习题[M].北京：清华大学出版社，2005.

[6]王知行.机械原理[M].北京：高等教育出版社，2000.

[7]王宏波，李建群.哲学教程[M].西安：西安交通大学出版社，2004.