一种改进蚁群算法在TSP问题上的应用
2018-12-23矫德强常淮阳
矫德强,常淮阳
(长春工业大学 电气与电子工程学院,吉林 长春 130012)
一种改进蚁群算法在TSP问题上的应用
矫德强,常淮阳
(长春工业大学 电气与电子工程学院,吉林 长春 130012)
针对蚁群算法存在的收敛速度慢和容易陷入最优解的问题,用遗传算法与非线性寻优来优化蚁群算法。在蚁群完成初始迭代之后,所有路径构成的解为初始种群,然后经过遗传算法进行选择、交叉、变异之后,去提升全局搜索的能力。最后,使用非线性寻优算法增强算法局部搜索的能力。通过这样的改进达到改善蚁群算法收敛速度及容易陷入最优解的问题,经过这样改进之后应用在旅行商问题上。
改进蚁群算法;TSP问题;机器人;算法优化
1 对算法的改进
1.1 算法改进的思路
遗传算法是一种比较常用的随机搜索算法,在机器学习方面有很好的应用,能在很大程度上减少陷入局部最优的情况。经典非线性规划算法采用梯度下降的方法进行求解,局部搜索能力较强。因此,本文提出的改进算法结合3种算法的优点,首先,蚁群算法快速地完成初始路径的选择,所有路径作为一个初始群落,然后,作为遗传算法的初始种群进行全局搜索,最后,在经过一定代数的迭代之后,利用非线性规划算法去进行局部搜索。通过这样的算法改进TSP问题最优路径的选择。
1.2 算法的具体实现
根据算法改进的思路,可画出算法的流程图,见图1.
其算法的步骤具体如下。
步骤1,对参数进行初始化。
对改进算法的各个参数进行初始赋值。
步骤2,解空间构造。
在蚁群算法完成初次寻径这一过程中,到达终点的蚂蚁所经过的路径组成的集合就是解空间,也是遗传算法的初始种群。
步骤3,如何选择下一节点?
首先,可以假设有m只蚂蚁从起点S出发最后到达终点T.一只蚂蚁在现在位置,下一刻的位置j如何选择?
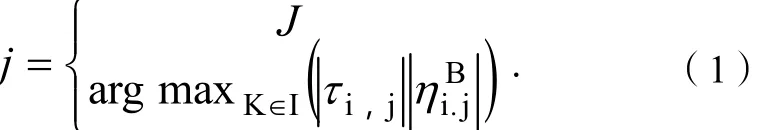
通过下面公式计算到达节点j的转移概率:
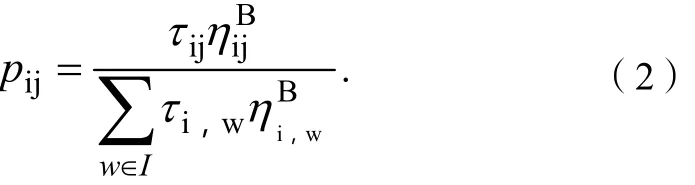
步骤4,和遗传算法结合。
将上述步骤构造的解空间作为遗传算法的初始种群,然后将初始种群通过编码表示成遗传空间的染色体或者个体,最后求得遗传算法的适应度函数,通过适应度函数的大小判断个体的好坏。适应度函数为:

选择操作是指在一定的概率下选择种群中的个体组成新的种群,通过进化得到更加优秀的下一代个体。某个个体被选中的概率为:

式(4)中:Fi为个体i的适应度值;N为种群个体的数目。
交叉操作是在种群中随机选择2个个体,通过交换组合,继承操作前2个个体的优点,进而产生新的优秀个体。第k个染色体αk和第l个染色体αl在j位进行交叉操作的方法为:

式(5)(6)中:b为[0,1]的随机数。
变异操作是指种群中的一个体发生一点变异,形成一个更好个体的过程。种群中某一个体i的某一基因片段j发生变异的操作为:

步骤5,信息素更新。
信息素更新策略主要指实时信息素更新和全局路径信息素更新。
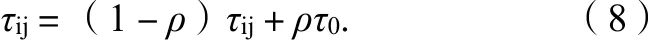
式(8)中:ρ为区间[0,1]的可以调节的参数;τ0为信息素初始值。
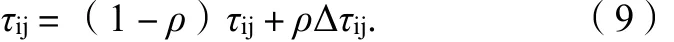
式(9)中:Δτij=1/L*,L*为所有路径中最短的一条的长度;ρ为[0,1]区间内的可调参数。
步骤6,非线性寻优。
在遗传算法进化到20代后,将此时所得的结果作为非线性寻优的初始值,然后用MATLAB优化工具箱中的线性规划函数对目标函数进行局部寻优,最终得到所求的最优解。
2 仿真结果
本文用改进的蚁群算法对TSP问题进行了求解,分析了改进后新算法的优点。设定20个节点坐标:(5,6)、(25,12)、(8,23)、(11,8)、(30,2)、(21,4)、(19,20)、(8,10)、(3,14)、(30,9)、(25,26)、(15,16)、(20,6)、(33,9)、(22,0)、(0,18)、(36,3)、(18,23)、(34,15)、(27,14)。改进算法的仿真结果如图2所示。

图1 改进算法流程图
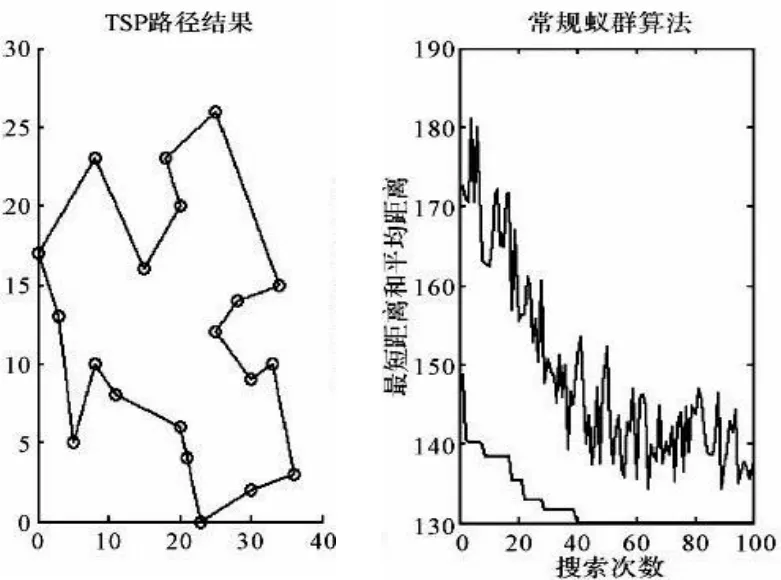
图2 改进算法在TSP问题上的仿真结果
3 结束语
本文通过对蚁群算法经过遗传算法和非线性规划的改进,增强了算法的搜索能力,加快了收敛速度,同时避免了陷入局部最优。实验证明,改进蚁群算法能提高精确度,增强自我搜索能力。
TP301.6
A
10.15913/j.cnki.kjycx.2018.01.145
2095-6835(2018)01-0145-02
〔编辑:刘晓芳〕
