数学问题解答
2018-12-21
2018年10月号问题解答
(解答由问题提供人给出)
2446已知实数a满足:有且仅有一个正方形,其四个顶点均在曲线y=x3+ax上,试求该正方形的边长.
(湖北省谷城县第三中学 贺 斌 441700)
解设正方形的四个顶点为A,B,C,D,那么ABCD的中心为原点O.否则,由于y=x3+ax为奇函数,因此A,B,C,D关于O点的对称点A′,B′,C′,D′也在曲线上,且A′B′C′D′也是正方形,与题设矛盾.
设A(x0,y0),B(-y0,x0),C(-x0,-y0),D(y0,-x0),
其中x0>0,y0>0,于是有
(1)
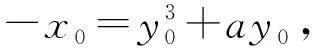
(2)
(1)×x0+(2)×y0得
(3)
由上式便知a<0.
(1)×y0-(2)×x0得
(4)
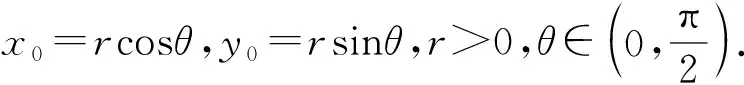
由(3),(4)式,得
a=-r2(1-2sin2θcos2θ),
从中消去r2,得关于sin2θ的方程
(1+a2)(sin22θ)2-(4+a2)sin22θ+4=0.
因sin22θ在(0,1)内只有一个根,所以
Δ=(4+a2)2-16(1+a2)=a4-8a2=0,
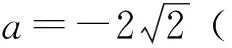
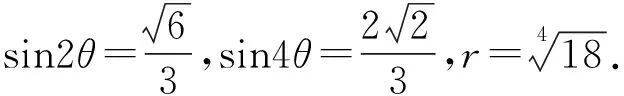
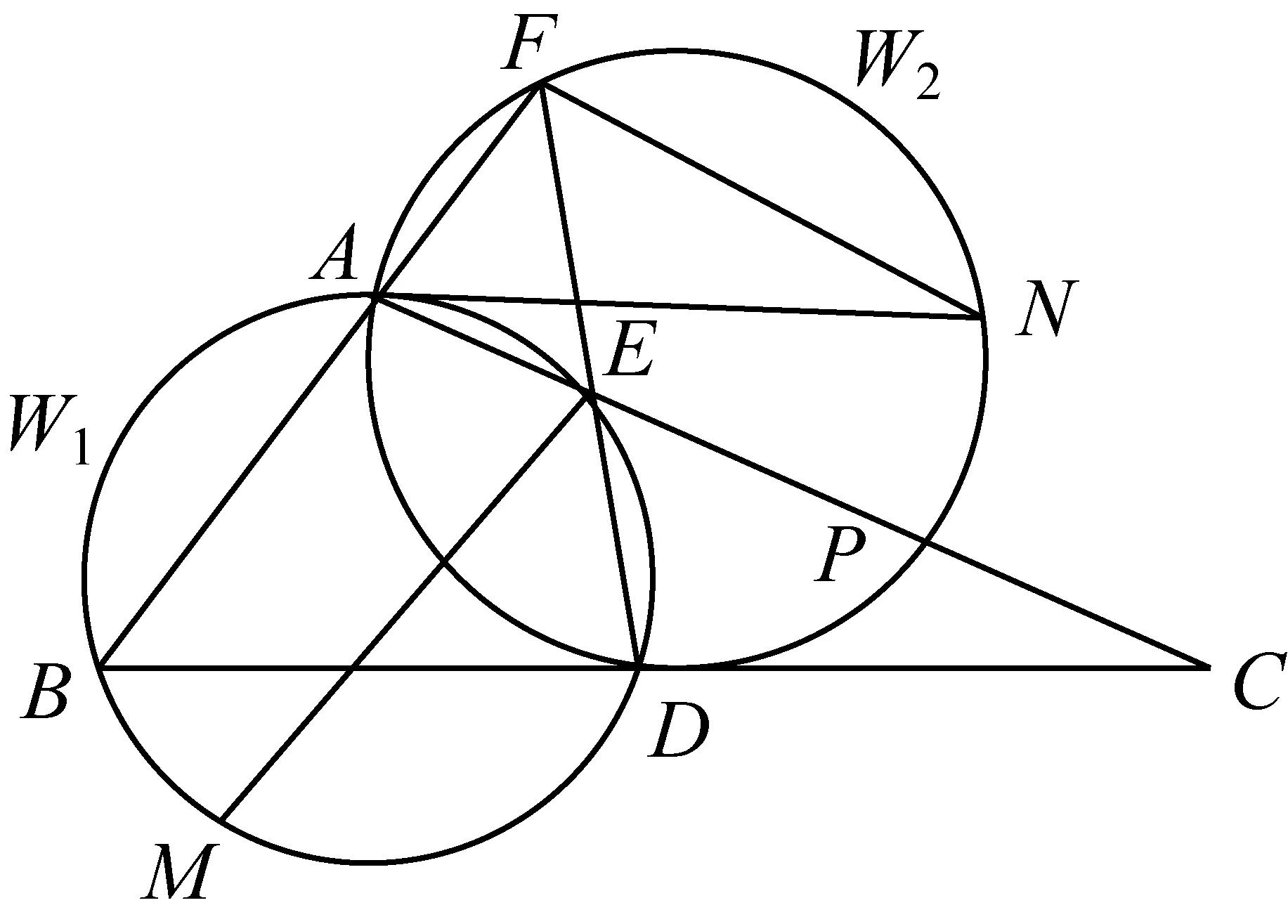
2447如图 ,已知△ABC的边BC上的中点D,过D的直线交AC和BA的延长线分别于E、F,且AB=EC-AE.过A、D、E三点的⊙W1和过A、D、F三点的⊙W2,.有EM∥BF、FN∥AC,EM、FN分别交⊙W1和⊙W2于M、N.求证:点D是过A、M、N三点圆的圆心.
(江西省高安市石脑二中 王典辉 330818)
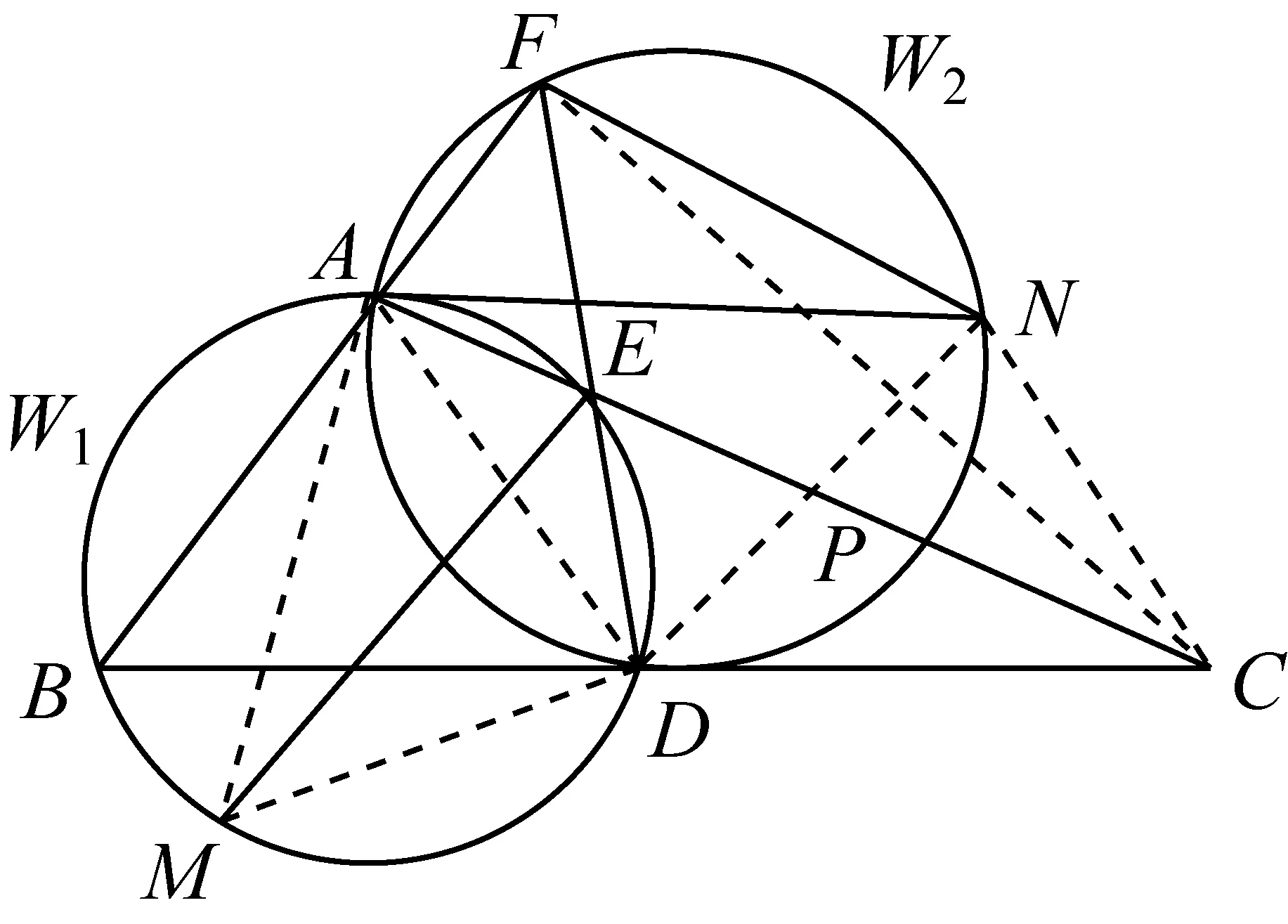
证明连接AD、AN、NC、FC、DN,AC与DN相交于点P.
由于FN∥AC,有S△ECF=S△ECN.
又因为S△BDF=S△DCF,
所以S△BDF=S四边形DCNE.
所以BF·ADsin∠BAD=BF·ADsin∠DNF
=EC·DNsin∠DPE
=EC·DNsin∠DNF.
即BF·AD=EC·DN.
①
在△AEF和△DAN中,
∠AFD=∠AND,∠DAN=∠DFN=∠AEF,
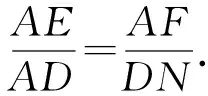
②
把①×②,得BF·AE=AF·EC,
(AB+AF)·AE=AF·(AB+AE),
有AE=AF,所以 ∠AEF=∠AFE.
连接AM,DM,
因为EM∥BF,有∠AFE=∠MED,
而A,M,D,E四点共圆,
有∠AEF=∠AMD,∠MED=∠MAD,
所以 ∠MAD=∠AMD,得AD=MD.
又FN∥AC,有∠AEF=∠DFN=∠AFE,
而A、F、N、D四点共圆,
有∠DFN=∠DAN,∠AFE=∠AND,
所以 ∠AND=∠DAN,有AD=ND,
所以点D是过A、M、N三点的圆的圆心.

(兰州大学数学与统计学院 冯建波 730000)
证明观察可知不等式在a=1,b=1,c=0,d=0及其循环取等.
a,b待定.
为了使得取等条件在x=1或者x=0.
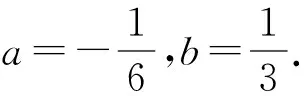

这显然在x为正数时候成立,回到原题有
证毕.
2449设a,b,p,q>0,且a+b=p+q=1,求证:
(1)
(河南质量工程职业学院 李永利 467000)
证明由a+b=p+q=1可得
=(ab)1-p=(ab)q,
(2)
(3)
由(2),(3)两式可知(1)式等价于
(4)
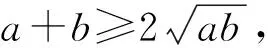
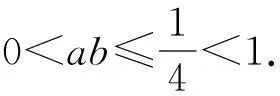
而由q>0可知,
幂函数f(x)=xq在区间(0,1)内单调递增,
故(4)式成立,从而(1)式成立.
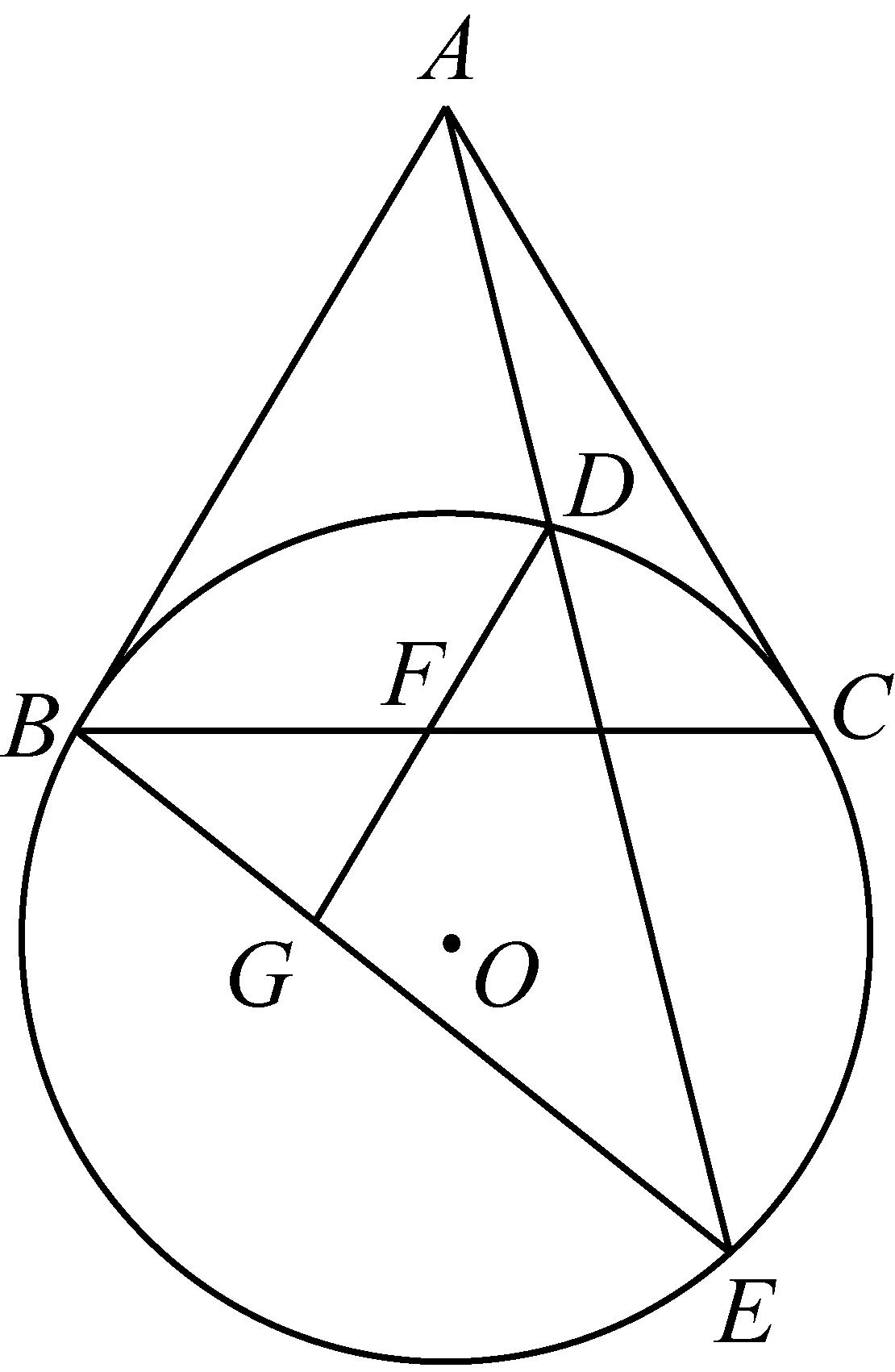
2450如下图,AB、AC分别切⊙O于B、C,过A作割线交⊙O于D、E,过D作AB的平行线分别交BC、BE于F、G,求证:F是DG的中点.
证明如图,过B作AE的平行线交⊙O于H,
连结HC交AE于I,则∠BHC=∠AIC.
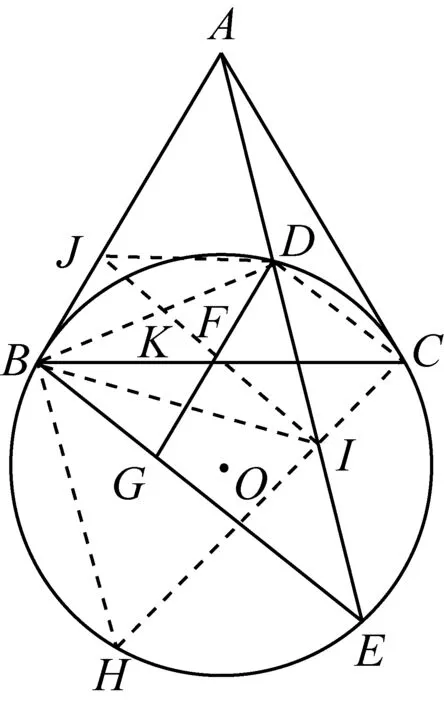
因为AB、AC分别切⊙O于B、C,
由切线长定理和弦切角定理,
有AB=AC,①
∠ABC=∠BHC,
所以 ∠ABC=∠AIC,②
所以A、B、I、C四点共圆.
由①, ∠AIB=∠AIC,
由②, ∠AIB=∠ABC.③
过D作BC的平行线交AB于J,
由已知,BFDJ是平行四边形,
连结JI交BD于K,④
所以 ∠BJD+∠ABC=180°.
由③,∠BJD+∠AIB=180°,
所以B、J、D、I四点共圆,
所以 ∠JBD=∠JID.
在⊙O中,再由弦切角定理,
有∠JBD=∠BED,
所以 ∠BED=∠JID,所以JI∥BE.⑤
由已知DG∥AB及②,
有∠DFC=∠ABC=∠AIC,
所以D、F、I、C四点共圆,连结FI,
所以 ∠CFI=∠CDI=∠CBE,
所以FI∥BE.
再由⑤得,J、F、I三点共线,
再由④得,K是BD的中点,
从而,KF是△BDG的中位线,
即F是DG的中点.
2018年11月号问题
(来稿请注明出处——编者)
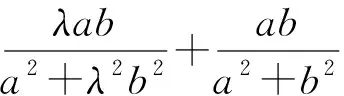
(浙江台州市洪家高级中学 邬天泉 318015)
2452如图,△ABC的内切圆与边BC,CA,AB分别切于点D,E,F,线段ED和AB延长后交于点M,线段FD和AC延长后交于点N,点P,Q分别为线段FM,EN的中点,点X,Y分别在边AB,AC上且满足XB=YC=BC,证明:XY∥PQ.
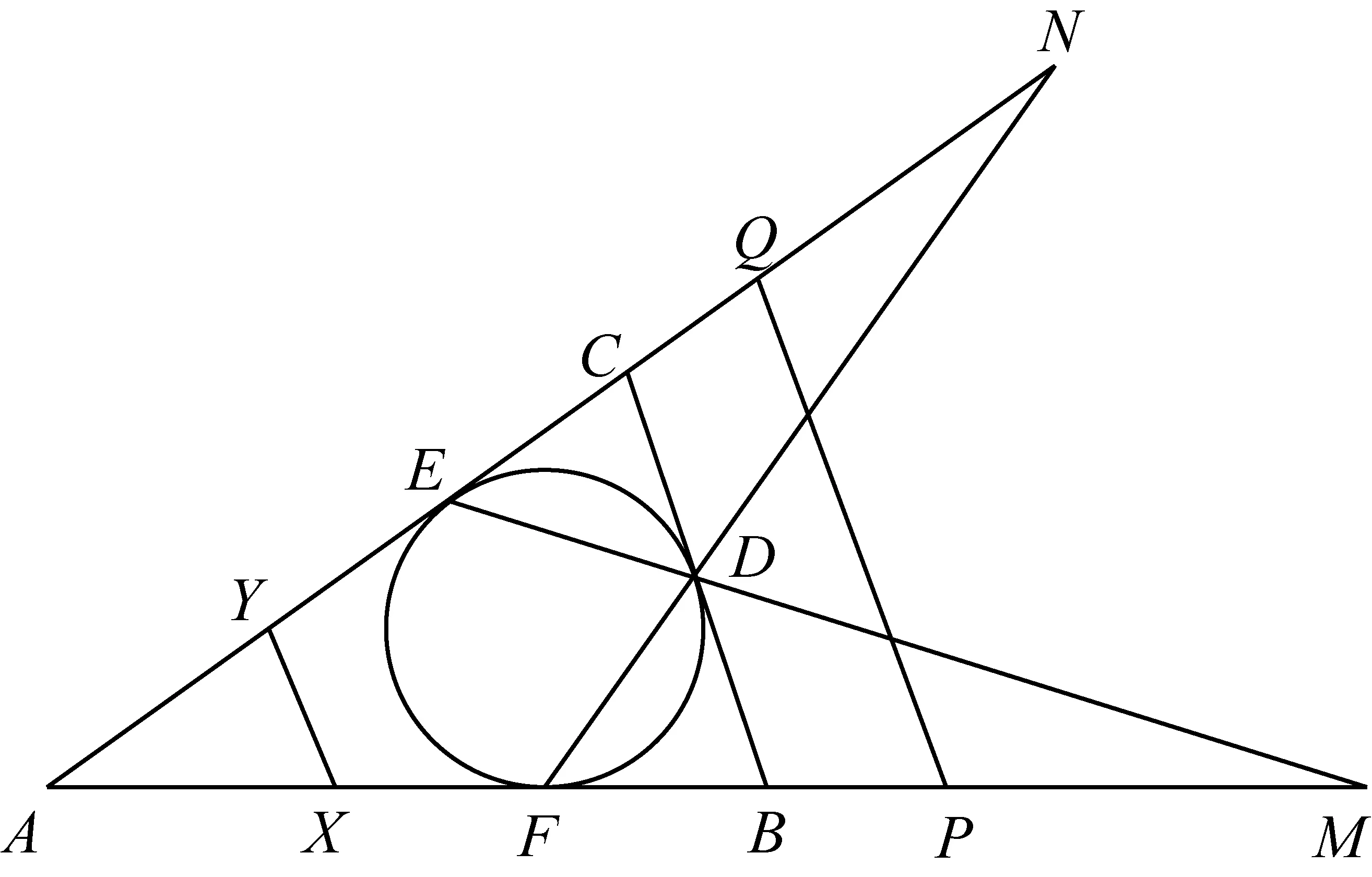
(河南省辉县市一中 贺基军 453600)
2453已知a、b、c为正实数,试证:
(*)
(浙江湖州市双林中学 李建潮 313012)
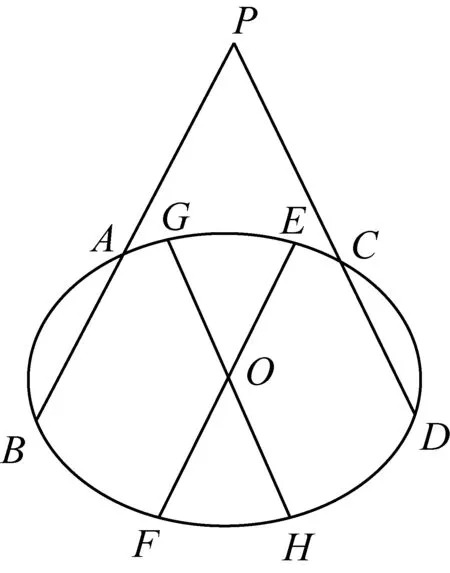
2454设点P为不在椭圆Γ(其中椭圆中心为点O)上的一点,过点P的直线PAB、PCD分别与椭圆Γ相交于点A、B,C、D,EOF与GOH分别为椭圆Γ中平行于两直线PAB、PCD的直径.
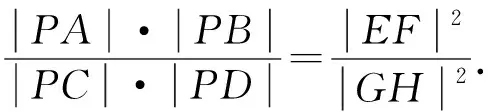
(安康学院数学与统计学院 赵临龙 725000)
(江苏省启东市汇龙中学 倪红林 226200)
