例谈数学教学中慢与快的辩证法
2018-12-21沈吉儿
郑 瑄 沈吉儿
(1.浙江省宁波市江北区教育局教研室 315020 2.浙江省宁波教育学院 315000)
朱光潜先生在《人生的艺术化》中这样写道:
阿尔卑斯山谷中有一条大汽车路,两旁景物极美,路上插着一个标语劝告游人说:“慢慢走,欣赏啊!”许多人在这车如流水马如龙的世界过活,恰如在阿尔卑斯山谷中乘汽车兜风,匆匆忙忙的急驰而过,无暇一回首流连风景,于是这丰富华丽的世界便成为一个了无生趣的囚牢.这是一件多么可惋惜的事啊!
无独有偶,歌手梁静茹有一首歌,名为《慢慢来,比较快》,歌中唱到:
让葡萄慢慢晕开,酿成芳香再醒来;让时间慢慢晕开,酿成智慧喝起来.
有些事其实急不来.等知了蜕变归来,等蝉声夏夜散开.
慢慢来会比较快.
放空慢慢来,专注比较快;放心慢慢来,别惊动未来.
慢慢来,慢慢比较精彩.
前者是美学境界所在,后者是技艺睿达所致.若能悟道,都是好.
对于数学课堂教学而言,同样有着慢与快的辩证关系.慢一点,才能使学生欣赏到数学世界的如画风景;慢慢来,才能使学生体验到数学思考的真谛,进而插上理性思维、创新思维的翅膀,更快地抵达数学学习的彼岸.
在近期的一次中考复习专题研讨活动中,笔者的亲身实践再一次加深了这样的体悟.
1 教学过程的简要回顾
宁波市自2007年中考开启“新定义”题型的新篇章,如今每年都以“新定义”题为中考压轴题,但这类题目是学生失分的痛点,也是老师教学的难点.因此,笔者以“中考‘新定义’题型的解答”为题,讲授了一节初三中考专题复习课,试图通过本节研究课,引导我区教师研究“新定义”题型的数学本质,明确其考查目的,掌握其教学方法,从而切实提高复习效果.
教学中,笔者首先阐明“新定义”题型在中考中的地位和考查目的,利用下表呈现了宁波市历年来“新定义”题型的相关信息:
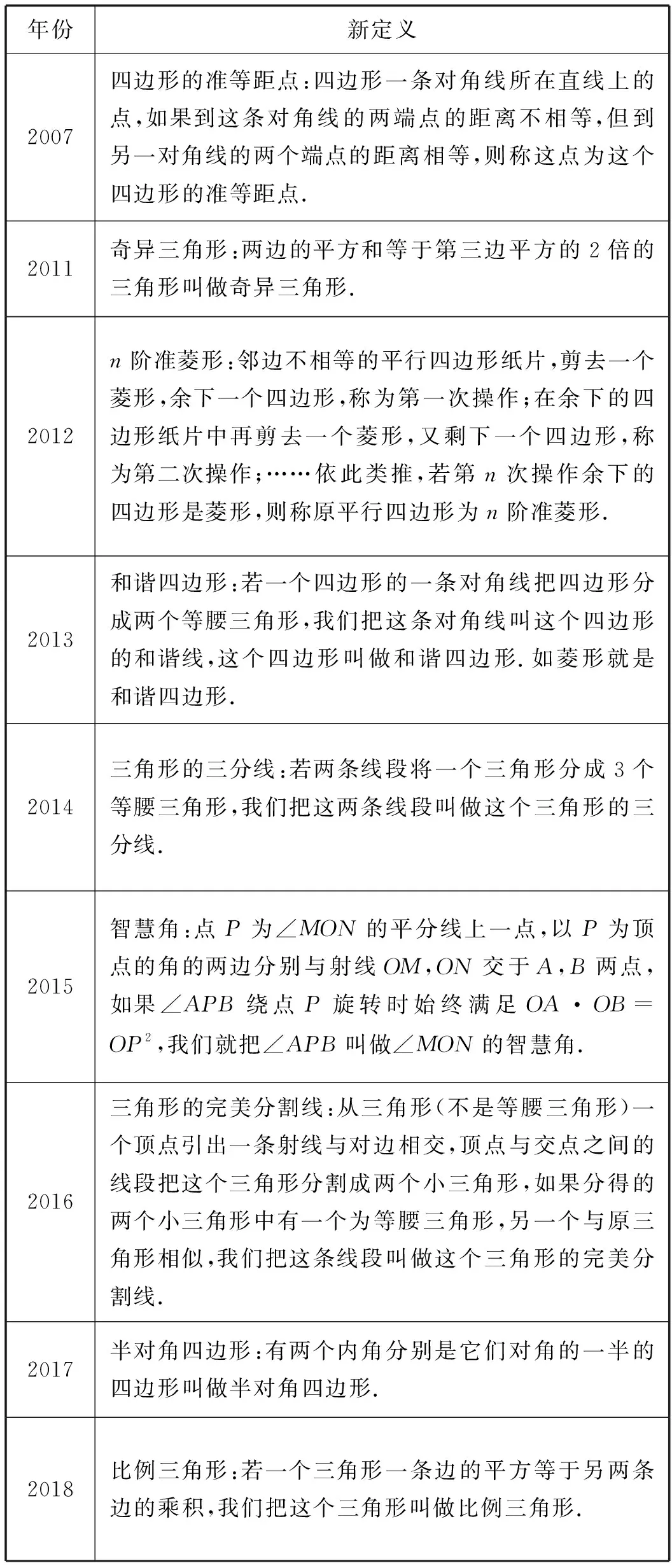
年份新定义2007四边形的准等距点:四边形一条对角线所在直线上的点,如果到这条对角线的两端点的距离不相等,但到另一对角线的两个端点的距离相等,则称这点为这个四边形的准等距点.2011奇异三角形:两边的平方和等于第三边平方的2倍的三角形叫做奇异三角形.2012n阶准菱形:邻边不相等的平行四边形纸片,剪去一个菱形,余下一个四边形,称为第一次操作;在余下的四边形纸片中再剪去一个菱形,又剩下一个四边形,称为第二次操作;……依此类推,若第n次操作余下的四边形是菱形,则称原平行四边形为n阶准菱形.2013和谐四边形:若一个四边形的一条对角线把四边形分成两个等腰三角形,我们把这条对角线叫这个四边形的和谐线,这个四边形叫做和谐四边形.如菱形就是和谐四边形.2014三角形的三分线:若两条线段将一个三角形分成3个等腰三角形,我们把这两条线段叫做这个三角形的三分线.2015智慧角:点P为∠MON的平分线上一点,以P为顶点的角的两边分别与射线OM,ON交于A,B两点,如果∠APB绕点P旋转时始终满足OA·OB=OP2,我们就把∠APB叫做∠MON的智慧角.2016三角形的完美分割线:从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中有一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.2017半对角四边形:有两个内角分别是它们对角的一半的四边形叫做半对角四边形.2018比例三角形:若一个三角形一条边的平方等于另两条边的乘积,我们把这个三角形叫做比例三角形.
通过例举分析上述“新定义”的共性,帮助学生梳理出它们的结构特征:赋予几何图形的元素以某种特殊关系而给出“新定义”,再从定义出发,研究这类图形的有关性质与判定,最后利用定义、性质和判定解决有关问题. 这与学生初中三年几何图形学习和研究的途径、方法一脉相承.因此,解答“新定义”问题,就是要调动已有的研究一个几何对象(如相交线和平行线、三角形、平行四边形、圆等)的经验,在理解“新定义”的基础上明确研究对象的本质特征,再利用已学的平面几何知识分析和解决后续的问题.解决此类型题目的关键,一是要切实理解“新定义”的内涵,把握研究对象的本质特征;二是要灵活运用已有数学知识,特别是有关的数学思想方法,创造性地分析和解决问题.新定义重在理解,新研究彰显能力.
在学生对“新定义”题型有了一个宏观认识,建立了适当的“先行组织者”后,笔者再以天津市、北京市2017年的中考“新定义”题为载体,和他们一起展开解答“新定义”题型的探究之旅.
2 发人深省的师生对话
在教学过程中,笔者与学生们的一个对话环节,颇有意味,发人深省,值得反思与考量.
师:同学们,我们刚才完成了第(1)小题,接下来,我们怎么做?
生1:接着做第(2)题.
师:马上做第(2)题吗?
众生:迟疑、环顾……
生2:(沉吟半晌)嗯,难道不是做第(2)题吗?
生3:将第(1)题的答案写下来.
众生:哄笑……
师:哦哦,我这个问题没有问好.
笔者的教学预设是在此师生有一个停顿,做一个检审,使学生体悟具体中蕴含的一般性,为后续的解答铺垫思路,所谓数学本质的探究和通透是也.但是冷场和跑马,使得笔者马上自觉地落到尘埃反省检点,继而收回发问鞠躬抱歉.
章建跃博士在课后点评时说:在教师最初给出“接下来,我们怎么做?”这一问题之时,我知道教师的意图是希望学生回顾一下思考过程,从具体中得到一些一般思路和方法,为解答下面的一般性问题做好准备,但是学生不明就里.这里,不是郑老师的问题没有问好,事实上,她问了一个好问题.但学生之前可能较少受到回顾解题过程、检审思路、归纳问题本质等方面的训练,所以没有养成“反思”的学习习惯.
许多时候,我们为了能让学生多刷几个题目而匆匆疾行,快节奏的过程中少了思维的回旋和反省的余地,最终收获甚微,事倍功半,特别是失却了对数学内在规律的回味、发现和品赏.
3 两则解题教学案例的深度思考
如何让学生感知、感悟、感动于数学教学中慢与快的辩证法?
笔者选择重庆市、北京市2017年中考的“新定义”试题,作为给予学生体悟“慢与快”的教学载体,试图以此说明,教学中应如何把握思维节奏,引导学生在停顿、回望与品赏中,领悟解题的真谛.
3.1 重庆市2017年中考第25题的教学分析
题目:对任意一个三位数n,如果n满足各个数位上的数字互不相同,且都不为零,那么称这个数为“相异数”.将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和与111的商记为F(n).例如n=123,对调百位与十位上的数字得到213,对调百位与个位上的数字得到321,对调十位与个位上的数字得到132,这三个新三位数的和为213+321+132=666,666÷111=6,所以F(123)=6.
(1)计算:F(243),F(617).
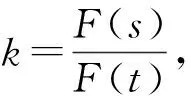
3.1.1 新定义重在理解
新概念“相异数”中的“异”,即不同,顾名思义,其义自见,学生比较容易忽视的是各位数字都不能为零;而新运算“F(n)”的理解,关键在于对研究对象进行有序地思考. 可以考虑依次先让个位、十位、百位上的数字不变,如此达成不重不漏.F(n)的得到,不是散漫飘忽的找寻,而是逻辑理性的求索,有利于培养良好的思维习惯.
题目条件中给出的“例如n=123,……求得F(123)=6”,旨在用实例来帮助学生更好地理解新定义.但是,教学中发现,其缺陷在于强化了范例的模仿作用,可能会阻碍学生自然探索研究对象本质特性的有效思维.
3.1.2 新研究彰显能力
确实,几乎所有的学生都能模仿完成第(1)题的计算,在诸如F(243)、F(617)的重复计算中,学生们会有些许运算上的失误.当然,也是几乎所有的学生都迫不及待地进入第(2)题的计算.显然,第(2)题,因为有了字母x、y的加入,同时还有s、t、k等参量进来,一时落英缤纷,分类讨论时繁复了许多,学生们出现了更多运算上的失误.
此时,笔者引导学生稍作停顿,再一次回过头来仔细审视此“新定义”.同时建议从代数层面探索F(n)的性质.(事实上,已经有一些学生在此处逗留,并自然地尝试以代数探究.)
假设:此三位数的百位数字为a,十位数字为b,个位数字为c,记作n=100a+10b+c.
于是:F(n)=(100a+10c+b+100c+10b+a+100b+10a+c)/111=111(a+b+c)/111=a+b+c.
原来,F(n)就是此三位数每个数位上的数字之和!
那么,(1)F(243)=2+3+4=9,F(617)=6+1+7=14;(2)F(s)=x+6,F(t)=6+y.
后续的问题解决轻捷而顺畅……
等知了蜕变归来,等蝉声夏夜散开.让时间慢慢晕开,酿成智慧喝起来.
有些事其实急不来.慢慢来会比较快.慢慢来,慢慢比较精彩.
当笔者让梁静茹的歌声《慢慢来,比较快》在教室里荡漾传播开来时,师生都会心地笑靥如花了.果然,慢慢来,比较快!
3.2 北京市2017年中考第29题的教学分析
题目:对于平面直角坐标系xOy中的点P和图形M,给出如下的定义:若在图形M上存在一点Q,使得P、Q两点间的距离小于或等于1,则称点P为图形M的关联点.
(1)当⊙O的半径为2时,
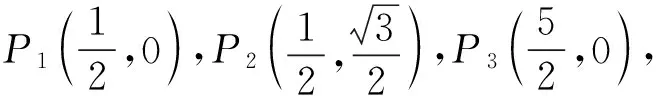
②点P在直线y=-x上,若P为⊙O的关联点,求点P的横坐标的取值范围.
(2)⊙C的圆心在x轴上,半径为2,直线y=-x+1与x轴、y轴分别交于点A,B.若线段AB上的所有点都是⊙C的关联点,直接写出圆心C的横坐标的取值范围.
3.2.1 新定义重在理解
笔者以为,学生对“关联点”或有两点疑惑:
其一,问题(1)、(2)中均未出现新定义中的关键词“图形M”,那么图形M是什么?由“⊙O的关联点”及“⊙C的关联点”的语境可知,新定义中的图形M,就是⊙O或⊙C.
简单的说:图形M就是一个圆.
其二,考量点P是否⊙O的关联点,关键在于能否在⊙O上找到一点Q,使得PQ≤1.
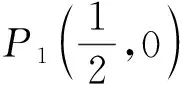
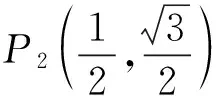
以上两个理解上的困难,事实上也是解题的难点所在.言必有据、算必有理,要将细节讲清楚,磨刀不误砍柴工.
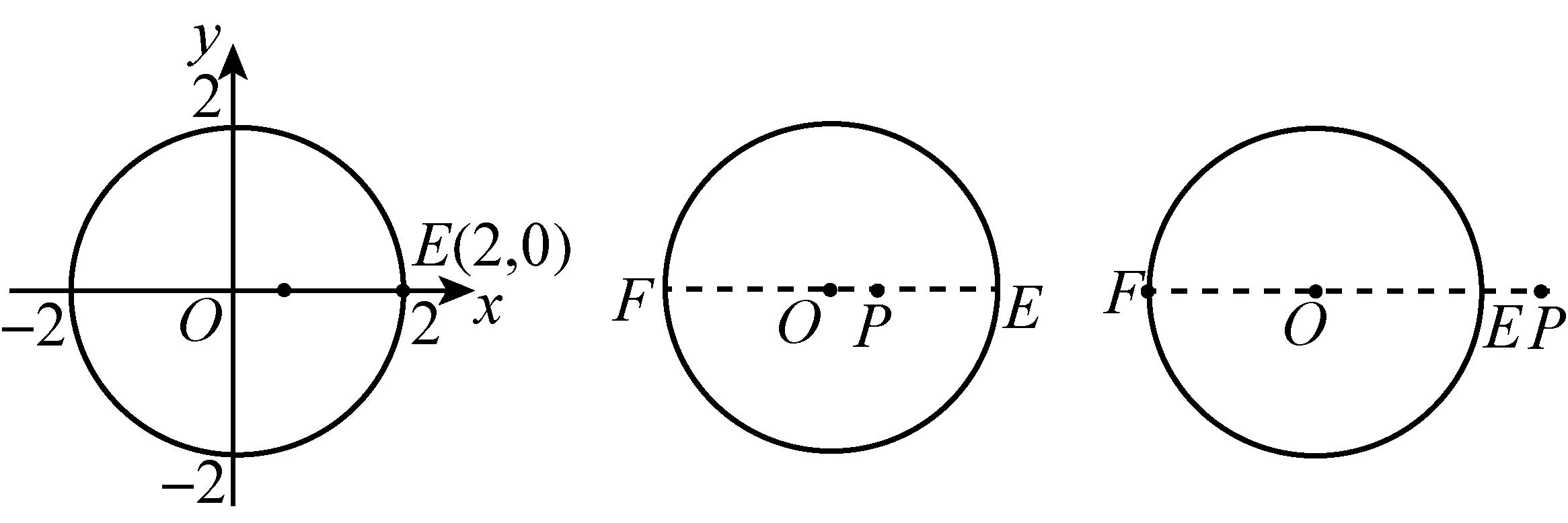
图1
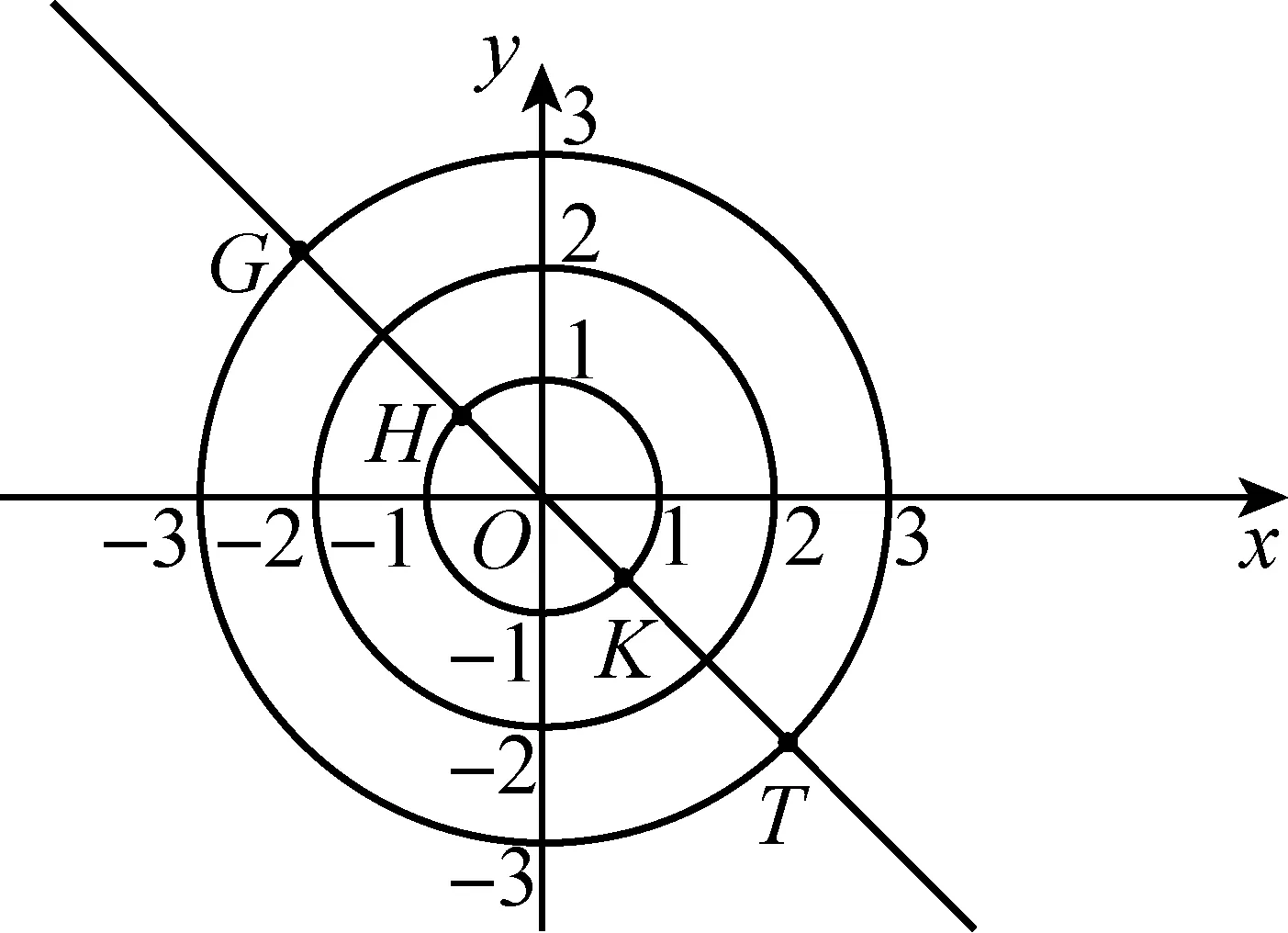
图2
3.2.2 新研究彰显能力
问题(1)①的解题经历和体验,正是学生从中可以得到诸多感悟的过程,尤其是对“关联点”性质的发现和研究,将对后续的问题解决提供极大的贡献.如若做了P1做P2,做了P2做P3,只走程序而未走心,那就无法得出“关联点”的本质.渐行渐思、且省且悟,这也是培养学生良好的学习习惯、思维品质和研究意识的契机.因此,仍然需要慢下来,等待奇观出现.
彼时彼刻,教师的功德,在于引导学生慢慢地、自然地、由衷地生发疑问:⊙O的关联点都在哪里?具有何种特性?这是对研究对象本质属性的追问,由此才能在解题中游刃有余.
Ok!圆环!学生通过独立思考、合作交流,终于提出:⊙O的关联点是以原点O为圆心,1、3为半径的圆环.精彩的发现.
仍然要将细节讲清楚:圆环(what)?为什么是圆环(why)?怎么想到是圆环(how)?数学教育家傅种孙先生的“然,所以然,何由以知其所以然?”是数学教师的教学准则.
好,现在,混沌世界已被澄明.(1)②中的点P在直线y=-x上,若P为⊙O的关联点,则点P必是直线y=-x落在圆环内的部分,即为线段GH、线段KT两端点的横坐标范围(见图2).
第(2)题,虽然⊙C的圆心在x轴上运动,但是由适才得到的研究对象关联点的性质可知,⊙C的关联点仍然是以点C为圆心,1、3为半径的圆环.要使定线段AB上的所有点都是⊙C的关联点,只要让线段AB落在圆环内部(包括边界)即可.
现在,学生清晰地看到,之前放慢解题的节奏和脚步,停顿、检审、研究而获得研究对象的性质,正适用于问题各种变式的解决,所谓万变不离其宗.看似减速,实质提速.
不妨再作停顿,继续思考一个值得关注的细节:当圆环沿着x轴从左往右运动时,哪些特殊位置恰好是线段AB落在圆环中的时刻呢?
直观地确定、简便地操作、严谨地计算是圆满解决此问题的要点.
有图有真相,无图靠想象.想象的结果是图3中的“相切”状态,学生会想当然地只考虑线段两端点的情形.因而辅之以图形,利用数形结合,恰能使得所有的状态清晰明了、达成精致.图3所示的四个位置,正是满足条件的四种特殊状态.
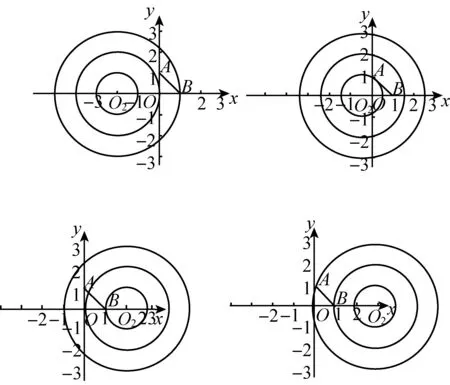
图3
但是,怎样才能简便地操作?圆环沿着x轴从左向右运动,那是一个说法,真正操作的层面,必将有画图的繁琐,怎么办?逆向的思路和方法是,圆动不如线动.圆环不动,而将线段AB沿着x轴从右往左运动,于是四个关键性的状态明晰如斯(如图4).
不断地回味和反思,优化解题思路,积累数学基本活动经验,培养数学思维品质.
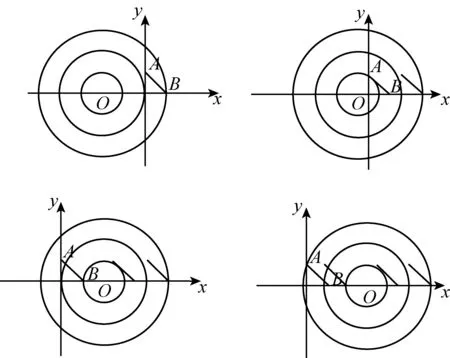
图4
4 感悟
通常,人们的感觉“快”总比“慢”好. 前者充满着激情和褒义;而后者似乎是懈怠与落后的象征. 事实上,快与慢是一对矛盾的两个方面,我们需要辩证地去看待和理解. 《论语·子路》中记载:“无欲速,无见小利. 欲速则不达,见小利则大事不成.”其中“欲速则不达”就是指:一味的性急求快,反而不能达到预期的目的. 孔子的这句话揭示了快与慢的辩证法.中国古成语中的“磨刀不误砍柴工”,当有此意.世间之事如此,数学课堂教学亦然.
数学学习和研究、数学教育和教学,没有解题万万不能,但是仅有解题远远不够.
章建跃博士真诚倡导:数学教师当示以学生思维之道!以“例题讲解 + 模仿练习”的方式让学生不断“重复着昨天的故事”, 其结果是让学生
作了大量的无用功,不仅事倍功半,而且严重影响学生学习数学的兴趣和自信心,挫伤他们的数学学习积极性,发展学生的核心素养也就成了一句空话.
于教师而言,题目如何能讲得完?!于学生而言,题目又如何能做得尽?!
重要的是:能在若干问题解决的历经、品析、反思、感悟过程中,得到灵动的习得和深刻的启迪. 其中,反思和感悟是一个慢慢参悟、内化、修炼、得道的过程,从而得以专于术、诚于道、游于艺,达至乘物以游心之境,领略欣赏数学之美.正如哲人所说:“慢些,我们就会更快.”
想起王国维《人间词话》中有言:“诗人对宇宙人生,须入乎其内,又须出乎其外.入乎其内,故能写之;出乎其外,故能观之.入乎其内,故有生气;出乎其外,故有高致.”文理之间居然是如此的相通.
最后,还是引用朱光潜先生在《人生的艺术化》中的文字:朋友,在告别之前,我采用阿尔卑斯山路上的标语,在中国人告别习用语之下加上三个字奉赠:“慢慢走,欣赏啊!”
