从“对话”的视角设计高三数学解题教学

李金蛟

(江苏省常州市第一中学 常州市李金蛟名师工作室 213003)

解题教学是高三数学教学的主要形式之一，师生都为此花费了不少精力，但现实中的教学效果却不尽如人意，不少学生的反映是上课听得懂但自己课后不会做，以致高考命题人员对高考的预期成绩与考生的实际表现经常存在较大的落差，问题的症结在哪里呢？在调查中发现：学生在解题中不能有效整合题目的信息，对题意的理解支离破碎，走不进题目描绘的“ 世界”中去，进入不了解题的“角色”，也就不能快速寻找到解题的思路.基于这样的认识，我尝试以心理学理论为指导，从“对话”的视角来设计解题教学的“话剧”，让学生分别“客串”不同角色(每个人也可以同时扮演多个角色)，和题目的相关元素进行“对话”，并为扮演的角色搜寻有价值的信息并展开换位思考，破译解题的“通关密语”，为解题进程寻找路线图，为角色设计辩护的“台词”，确定解题的最佳路径,让学生火热的思考去不断融化数学冰冷的美丽，激发了学生学习数学的兴趣，培养了学生解题后反思的习惯，提升了他们的思维能力，取得了理想的效果.下面结合自己平时教学中的几个案例，与大家分享自己的心得并请指正！

1 与命题者本人进行对话

数学题是人命制的，因此题目里不可避免地留下命题者的印记，或明或暗地体现了命题者的意图与设想，寻找命题者留下的编制“痕迹”与“破绽”，接收命题者传递给我们的信息暗示或指引，如有时为了控制题目的难度与得分，常在前面人为增加一问(实质是命题者为减少难度而设置的“台阶”)，如果你感受到命题者内心的思维活动与释放出来的“善意”，与其进行隔空“对话”，并进行判断、加工，你将露出会心的微笑：我翻译了命题者的思维密码，一切都明白了！

案例1设f(x)是定义在R上且周期为2的函数，在区间[-1，1]上，

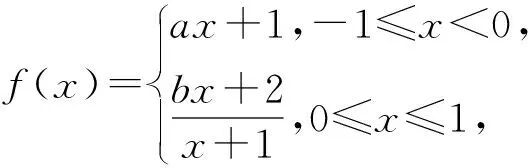
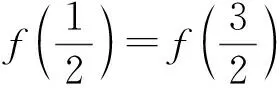
“解题者”：对于周期函数，必须要给出在一个周期长度区间上的解析式才能确定函数.本题中函数的周期为2，它仅告诉函数在[-1,1]上的解析式，好像是得不到新的方程啊.

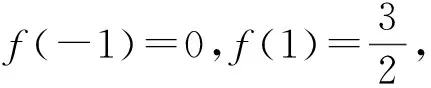
“命题者”：f(x)是定义在R上且周期为2的函数，给出在一个周期长度区间上的解析式，这个区间的两个端点只要给出其中一个，就能确定函数！

“解题者”：题目的条件设置应该是恰到好处，不应多余！周期函数给出的解析式在一个周期长度上，且只要包含两端点中任一个就能确定函数了，如两端点都包含其中，实际上就是告诉了我们一个等量关系，我也会命题了！

学生了解数学命题的一些基本方式与规律，掌握数学题改编的常见方法，不但有助于他们把握数学题的结构与特征，“看穿”命题者的意图，快速找到解题的钥匙，更可以自己编题练习，从一道题洞悉一类题的思想方法，提高分析问题、解决问题的能力.

2 与题目的条件(或结论)进行对话

题目的条件与结论是信息源，题目的条件(或结论)是观察题目的窗口，分析问题的突破口，解决问题的入口，与题目进行“对话”就是在理解题意的基础上展开联想，接纳同伴与自己内心的“质疑”，善于捕捉“异类信息”，如“吉祥”数字、特殊的无理数等蕴藏的信息，挖掘题目的内涵与“弦外之音”，绕过暗流险礁，寻找解决问题的突破口与绿色通道.

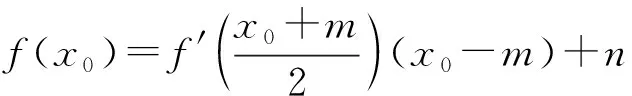
分析f(x)=aex+x2-2x，f′(x)=aex+2x-2，

假设存在一个定点(m，n)(m，n∈R)，

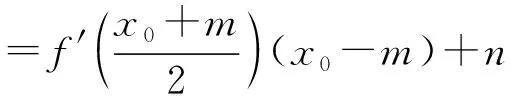
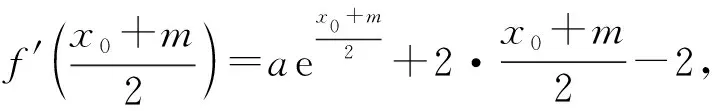
“条件”：题目的条件中为什么加上“x0≠m”？

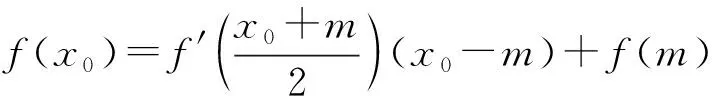
“条件”：如何证明？

学生：将x0=m代入方程得到一个恒等式即可.

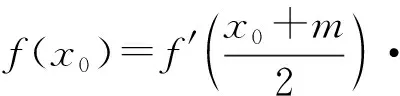
学生：说明f(x0)-f(m)也应含有因式(x0-m) .

“条件”：现在要研究的是当x0≠m时等式成立的问题，如何处理？

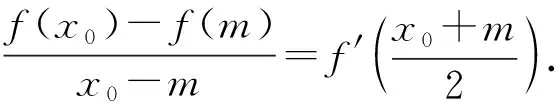
至此，学生明确了解题方向：

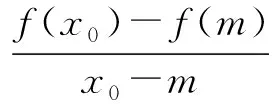
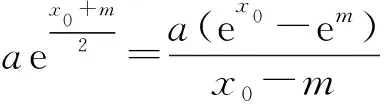
俗话说“无巧不成书”，许多数学题的条件(或结论)有其区别于其它题目的内部特殊结构或特征，我们找到它的特殊性，就能有助于我们发现珍藏解题思路宝库的窗户.

3 让题目的条件与结论进行对话

解题是一种认识活动，是对概念、定理的继续学习，是对方法技巧继续熟练的过程，而不仅仅是“规则的简单重复”或“操作的生硬执行”．每个数学题都是一首爱情小诗，条件与结论就象“ 一对恋爱中的男女”，我们就是“红娘”，要倾听他们各自表白的“心声”，在条件与结论之间架起联通的桥梁，让他们相互吸引、相互靠近、相互转化，最终实现相互融合．

案例3对于给定的正整数k,若数列{an}满足an-k+an-k+1+…+an-1+an+1+…+an+k-1+an+k=2kan对任意正整数n(n>k) 总成立，则称数列{an}是“p(k)数列”.(2)若数列{an}既是“p(2)数列”，又是“p(3)数列”，证明：{an}是等差数列. (江苏省2017年高考第19题第(2)问)

“条件”：由数列{an}是“p(2)数列”得，an-2+an-1+an+1+an+2=4an(n>2,n∈Z)①；由数列{an}是“p(3)数列”得，

an-3+an-2+an-1+an+1+an+2+an+3=6an(n>3,n∈Z)②.

“结论”：要证{an}是等差数列，即要证an-1+an+1=2an(n>1,n∈Z).

“条件”：因为②比①复杂，所以化简②比较方便，即将①代入消元，但如何消元呢？

“结论”：对照要证的结论，应有an-3+an-2+an+2+an+3=4an(n>3,n∈Z)，即需要消去an-3+an-2+an+2+an+3.

“条件”：由①要得到an-3+an-2+an+2+an+3=4an(n>3,n∈Z)，显然不能一次性完成.由①得an-2+an-1=4an-(an+1+an+2).

“结论”：要证{an}是等差数列，应消去an-3+an-2+an+2+an+3(重要的话重复一遍).

“条件”：由an-2+an-1=4an-(an+1+an+2)得an-3+an-2=4an-1-(an+an+1)(n>3,n∈Z);同理an+2+an+3=4an+1-(an-1+an)(n>3,n∈Z)

“结论”：要证{an}是等差数列，要证an-1+an+1=2an(n>1.n∈Z)(重要的话说三遍).

“条件”：还要对n=1与n=2进行认证.(下略)

寻找解题思路的过程本质上就是寻找条件知识与结论知识之间逻辑联系或转化轨迹的过程，在这个过程中，学生的解题与发展能力同行，经历了激活知识、检索知识、提取知识、运用知识的化学变化.

4 与题目的背景进行对话

数学来源于生活，更是人类的一种文化，数学题的背后隐含着丰富的文化内涵与资源，我们去体会、感悟、挖掘它们的内涵与意境，不仅可以更全面理解题意，体会数学在各方面的作用，而且将帮助我们快速找到解题的钥匙，提高分析问题的能力，更清晰地认识隐藏在题目背后的数学本质；而数学题的背景是多元的，甚至是混合的，限于篇幅，仅举以下几种类型进行说明.

4.1 与题目的几何背景进行对话

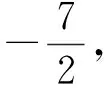
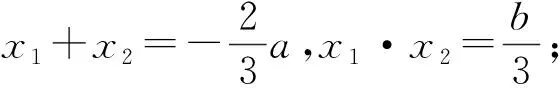
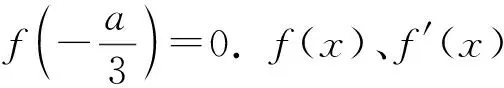
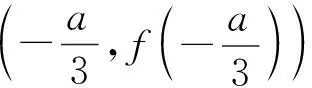
学生：由于f(x1)+f(x2)=0，所以f(x1)+f(x2)+f(x3)=f(x3)，目标明确了，有信心了，结果知道了，目标明确了，想算错都不可能了！

教师：但上述结论不是定理，因此不能直接用！

学生：这个可用韦达定理证明，与几何背景对话后知道有f(x1)+f(x2)=0，就象黑暗中射来一束光，我们可以看清方向和目标了！

4.2 与题目的物理背景进行对话

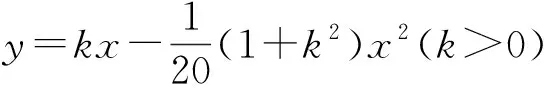
教师：此高考题有比较内隐的物理背景，当年的考生由于进入射击的情境而读不懂题意.因而不能进行正确的“数学化”，产生各种各样的错误.

学生：炮弹落地点的横坐标是什么意思？求最大射程中对应的变量是谁？

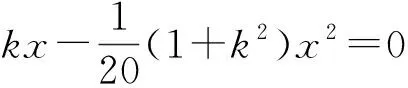
学生：“炮弹可以击中它”是什么意思？

学生：“它的横坐标a不超过多少时，炮弹可以击中它”又是什么意思？

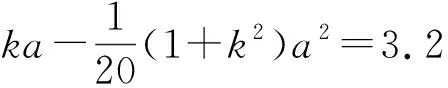
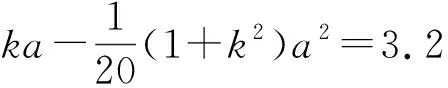
4.3 与题目的生活背景进行对话

案例6水管或煤气管的外部经常需要包扎，以便对管道起保护作用，包扎时用很长的带子缠绕在管道外部.若需要使带子全部包住管道且没有重叠的部分(不考虑管子两端的情况，如图1所示)，这就要精确计算带子的“缠绕角度α”(α指缠绕中将部分带子拉成图1中所示的平面ABCD时的α，其中AB为管道侧面母线的一部分).若带子宽度为1，水管直径为2，则“缠绕角度α”的余弦值为.(2008年苏州、无锡、常州、镇江第一次模拟考试第14题)

学生：“使带子全部包住管道”是什么意思？

“生活背景”：就是管道被带子完全覆盖.

学生：“没有重叠的部分”是什么意思？

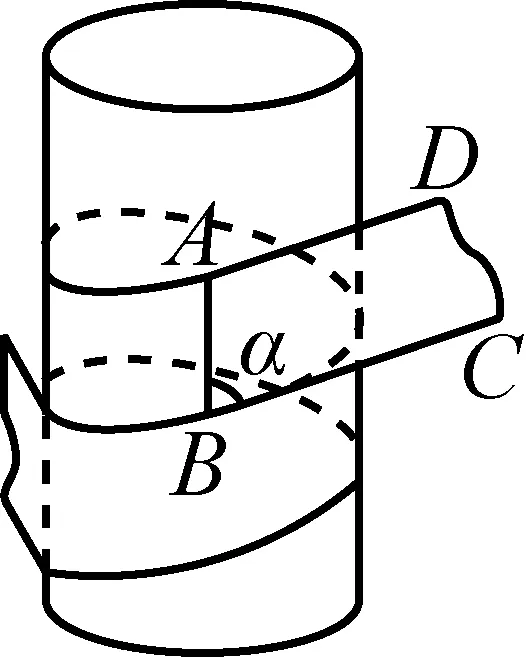
图1

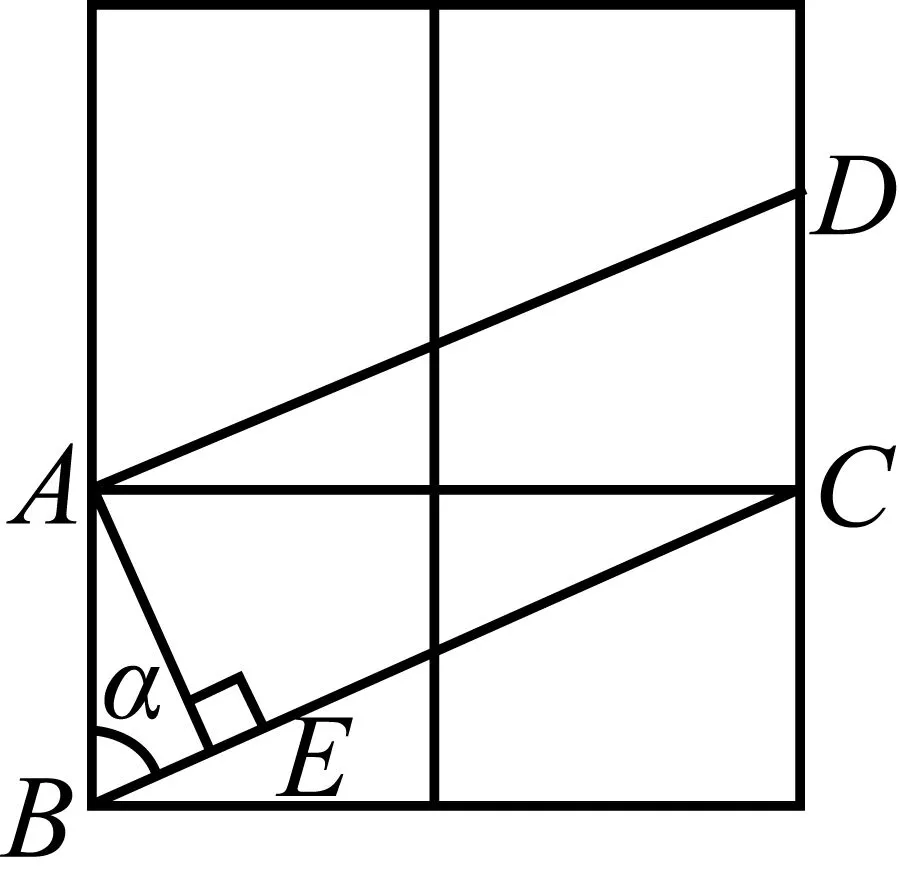
图2

“生活背景”：相邻的两个带子边界所在直线重合.

学生：“带子全部包住管道且没有重叠的部分”表示相邻的两个带子既不重叠，又紧紧相连，没有缝隙.

“生活背景”：说明相邻的带子的重合点A与C展开后是在同一水平线上.

从对话的视角设计高三数学的“解题舞台剧”，其本质是根据学生的心理特征，打造激发学生思维火花高速碰撞的“正负电子对撞机”，让他们以不同角色进行相互“对话”，推动他们以不同身份去观察、思考问题，对题目的各种信息进行加工、挖掘，多角度地对同一个问题进行不同方式的思考，引导他们交流思想，认清数学题目的本质，“走进”题目的“内心”，追求对题意更高层次的理解，在对话过程中体验寻找解题思路的心理历程，培养学生解题的“题感”，最终实现一个人独自承担多种角色与题目“对话”，亲身感受到数学的文化魅力，全面提升他们的数学核心素养！