小间距比下串列双圆柱涡激振动数值模拟研究：尾流和耦合机制

陈威霖， 及春宁， 许 栋

(天津大学 水利工程仿真与安全国家重点实验室，天津 300072)

当圆柱受到来流作用，从圆柱上脱落旋涡产生的流体力会激励弹性支撑或柔性圆柱发生振动，振动的圆柱会反过来作用于流体，这种圆柱与流体之间的耦合作用称之为涡激振动。圆柱后的尾流以及圆柱与流体之间的耦合作用成为其重要的研究方向[1-3]。尾流模式反映了圆柱与流体相互作用的结果，而两者之间的耦合作用则成为揭开涡激振动背后机理的关键；圆柱受到的流体力会影响其疲劳寿命[4-5]，也成为利用涡激振动发电的关键要素[6-8]。Williamson等[9]引入了定义圆柱后尾涡模式的方法，即根据一个周期内脱落旋涡的情况定义其模式，并被广泛采用。Williamson等[10]对单圆柱涡激振动的尾流模式进行了详细的归纳，主要包括2S(每个周期脱落两个单独的旋涡)，2P(每个周期从圆柱上脱落两个涡对)，2T(每半个周期内圆柱脱落两个旋转方向相同的旋涡和一个旋转方向相反的旋涡)和2C(圆柱两侧各释放一对旋转方向相同的旋涡，但两侧涡对方向相反)模式四种。此后，圆柱涡激振动的研究中又发现了一些新的尾流模式，比如P+S模式[11]和2Q模式[12]等。当雷诺数较低时，圆柱的响应呈现出初始和下端两个分支[13]，对应的尾流均为2S模式；由于在较远的下游，旋涡发生融合，下端分支的2S模式又称为C(2S)模式[14]。当雷诺数较高时，质量-阻尼系数成为影响圆柱响应的关键因素[15-16]：当质量-阻尼系数较低时，响应呈现出三个分支，分别为初始、上端和下端分支；而当质量-阻尼系数较高时，响应则仅为两个分支，分别为初始和下端分支。其中，初始分支对应2S模式，而上端和下端分支均为2P模式。需要说明的是在2P模式中，涡对中两个旋涡的强度并不相等，其中强度较弱的旋涡会很快消散。当涡激振动的圆柱质量比小于m*≤2.6以后[17]，响应出现超上端分支，其振幅达到了1.5D，此时对应的尾流模式为2T模式。

本文将继续对小间距比(L*=1.1～1.5)下串列双圆柱中的尾流模式和耦合机制进行深入的研究，以全面展示低雷诺数下小间距比串列双圆柱涡激振动背后的机理。基于此，本文将重点关注此前所述新现象的耦合机制，这是揭开串列双圆柱涡激振动机理的关键所在。

1 数值方法

1.1 控制方程

流体运动的数值模拟采用浸入边界法，无量纲的控制方程如下

(1)

(2)

对以上控制方程采用二阶精度的Adams-Bashforth时间格式进行离散，可得控制方程的守恒形式如下

(3)

(4)

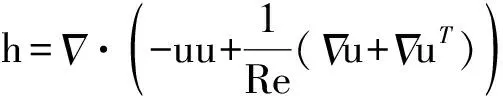
针对传统浸入边界法施加边界条件精度不高的情况，Ji等[25]提出了基于嵌入式迭代的浸入边界法，将浸入边界法嵌入到压强泊松方程的迭代求解中，利用压强的中间解比初始值更接近真实值的特点，迭代修正附加体积力，在不显著增加计算耗时的前提下，提高整个算法的求解精度。

对仅做横流向运动的刚性圆柱体，其无量纲运动方程可以用下述方程来描述

(5)

式中:y为无量纲位移;t为无量纲时间;m*为圆柱体质量比;FN=fnD/U∞为无量纲固有频率(fn为固有频率);ζ为结构阻尼比;Cl为圆柱受到的横流向流体力系数。方程采用标准的Newmark-β法求解。

以上流体和刚体运动控制方程采用圆柱直径D、来流速度U∞和流体密度ρ进行无量纲化。

1.2 问题描述

拟展开串列双圆柱涡激振动的数值模拟参数设置如下：两圆柱的间距比L*=L/D=1.1～1.5，雷诺数Re=U∞D/υ=100(其中υ为运动黏性系数)，折合流速Ur=U∞/fnD=3～30(最小间隔为ΔUr=0.5)，质量比m*=4m/ρπD2=2.0(其中m,ρ分别为圆柱的质量和流体的密度)。

Sen等[26]对圆柱绕流数值模拟研究发现，当阻流比B≤0.01时，阻流比对流动特征参数的影响不再重要。为此，本文采用的计算域宽度为100D，对应的阻流比为B=D/H=0.01。如图1所示，将计算域的坐标原点设在串列两圆柱距离的中心上，距离入口和出口边界为100D，距离上和下边界为50D。

图1 计算域与边界条件

采用正交笛卡尔网格对计算区域划分，X(流向)和Y(横向)方向的网格数分别为1 024和512，其中加密区域内无量纲网格尺寸Δx/D=Δy/D=1/64。加密区域为6.5D×4.0D，编号1和2分别为上游和下游圆柱。

计算域边界条件设置如下。入口边界为Dirichlet型边界条件(u=U∞,ν=0)；出口边界为Neumann型边界条件(∂u/∂x=0,∂v/∂x=0)；上下边界为自由滑移边界条件。此外，为满足Courant-Friedrichs-Lewy条件，即CFL=UmaxΔt/Δx≤0.5，其中，Umax为最大流速，Δt为时间步长，时间步长取为Δt=0.006。

2 方法验证

本文采用的数值模型和程序已从单圆柱绕流[27-28]，单圆柱涡激振动以及串列并列双圆柱[29-30]等多角度进行了验证，读者可自行查阅。

3 结果和讨论

3.1 尾流

如图2所示，当间距比L*=1.1时，串列双圆柱尾流随折合流速(响应)呈现明显的变化。当折合流速Ur=3.5时，两圆柱的响应几乎为零，上游圆柱脱落旋涡将两圆柱包裹在一起，在下游形成经典的卡门涡街(2S模式)；而当折合流速Ur=4.5时，两圆柱的响应达到了Yrms/D=0.17和Yrms/D=0.25水平上，此时从下游圆柱脱落的旋涡更加靠近圆柱底部，如图2(b)所示。随响应的增加，比如Ur=6.5，圆柱后脱落旋涡的长度增加，且并排两列旋涡的形成更加靠近上游，如图2(c)所示。当折合流速Ur=12.0时，两圆柱的响应已从最大响应下降，此时从圆柱两侧分离的剪切已经明显地互相作用，如图2(d)所示。在下侧未分离剪切层的影响下，圆柱上侧的剪切层分离为两部分，一部分保留在圆柱上侧而另一部分在圆柱下游形成旋涡。在折合流速Ur=12.0～25.0范围内，两圆柱的升力频率变得混乱，而圆柱后混乱的旋涡则从尾流的角度支持了该结论。当折合流速Ur=20.0时，一种新的尾流模式在圆柱下游形成，称之为为T+S模式。该模式的T由两个顺时针的负涡和一个逆时针的正涡组成，S则为正涡，如图2(g)所示。当折合流速进一步增加到Ur=22.0～30.0时，串列双圆柱偏离初始的平衡位置更远而使得其耦合作用愈加复杂，因此，圆柱下游的尾流也就更加混乱，如图2(h)～图2(i)所示。

需注意的是，高雷诺数单圆柱涡激振动在大振幅的上端分支形成2P模式，其原因为脱落的长旋涡由于受到拉伸而分裂为两个子涡；但在本文低雷诺数串列双圆柱涡激振动中下游圆柱的最大响应已经到了高雷诺数上端分支的大小，但脱落的长旋涡并未因拉伸而分裂，这是由于低雷诺数时流体的黏性要大于高雷诺数时的情况。

如图3所示，当间距比L*=1.2时，串列双圆柱尾流随折合流速(响应)的变化与间距比L*=1.1时相似。当折合流速Ur=5.0时，响应处在急剧增加的阶段，圆柱后旋涡靠近其底部，且在较近的下游即形成经典的卡门涡街；随旋涡向下游移动，尾涡逐渐消散，如图3(a)所示。而折合流速Ur=10.0时，圆柱的响应已经达到了Yrms/D=0.41和Yrms/D=0.61水平上，此时圆柱后脱落长旋涡，且旋涡之间的距离差不多8D要远大于折合流速Ur=5.0时旋涡之间的距离；说明此时旋涡脱落频率要小于折合流速Ur=5.0时的情况。一种新的尾流模式，P+S模式，出现在折合流速Ur=17.0时，由于受到下侧脱落旋涡的影响，其中圆柱上侧的旋涡分裂为两个子涡，强度较大的旋涡与圆柱下侧脱落的正涡组成一个涡对。单独的旋涡由于强度较弱很快消散掉，因此，P+S模式仅存在于圆柱下游的一段距离上。当折合流速Ur≥17.0以后，串列双圆柱的升力频谱出现多个频率，这是由于两圆柱之间平衡位置差已不再为零，上游圆柱两侧的旋涡同时与下游圆柱相作用；圆柱后旋涡混乱的排列很好地支持了该结论。

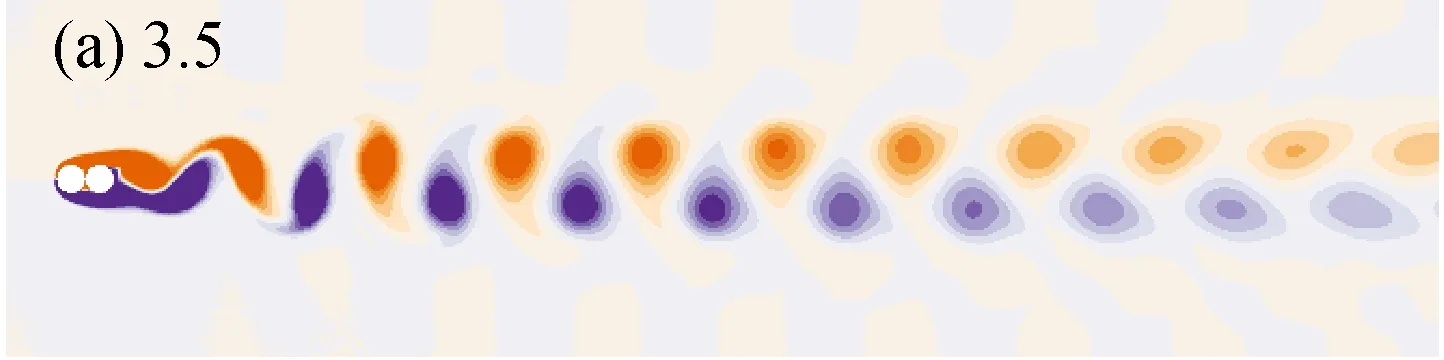
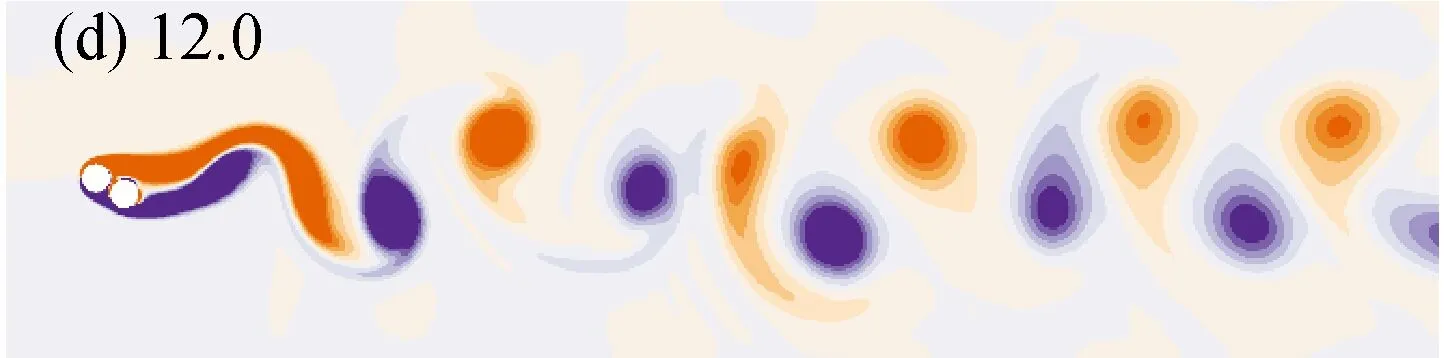
图2 间距比L*=1.1时，不同折合流速下串列双圆柱后的流场

Fig.2 Wake flow behind two tandem cylinders for different reduced velocities atL*=1.1

当折合流速Ur=22.0～30.0时，下游圆柱的响应处于随折合流速增加的类尾流弛振区域，此时上游圆柱脱落的旋涡与下游圆柱的同向旋涡相融合，这可能是促进下游圆柱响应随折合流速增加的动力。

如图4所示，当间距比L*=1.3时，串列双圆柱尾流在响应的前三个分支均比较规律，而在第四分支则有些混乱。当折合流速处于第一分支时，如Ur=3.0，上游圆柱的剪切层将两圆柱包括在一起，旋涡在下游圆柱脱落并形成2S模式，如图4(a)所示。此时两圆柱更像一个延展体，旋涡脱落时距离圆柱较远，因此，两圆柱受到的升力很小，使得两圆柱的振幅接近零。当响应进入第二分支，下游脱落旋涡很快形成并排两列的2S模式，如图4(b)所示。此时脱落的旋涡距离圆柱已经很近，因此，圆柱受到的升力也会显著增加，相应地两圆柱的振幅增加，明显大于第一分支。随着响应进入第三分支，如图4(c)所示。圆柱后脱落旋涡的强度增加，旋涡之间的距离也随之增加。此时两圆柱之间已经有剪切层形成，而形成的剪切层会促进下游圆柱上旋涡的脱落，因此，促进下游圆柱的振动，两圆柱的振幅相比于第二分支继续增加。当折合流速Ur=20.0时，响应来到第三分支的末端，圆柱脱落频率下降，因此，旋涡之间的距离也差不多2倍于折合流速Ur=9.5时的情况。当响应进入第四分支，圆柱升力的频谱变得不再规律，圆柱之间的耦合作用变得复杂起来；如图4(e)所示。当折合流速Ur=28.0时，圆柱下游混乱的尾流更是佐证了这样一点。此时从两圆柱上脱落的旋涡也距离两圆柱较远，从而使得两圆柱的振幅相比分支三出现突然下降，不再能维持在较高的振幅上。

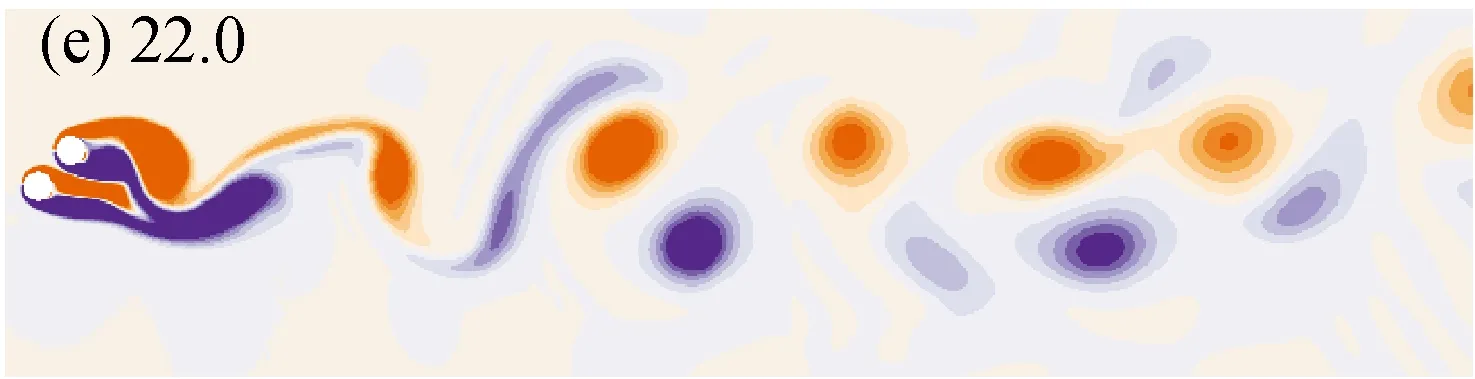
图3 间距比L*=1.2时，不同折合流速下串列双圆柱后的流场

Fig.3 Wake flow behind two tandem cylinders for different reduced velocities atL*=1.2

当间距比L*=1.5时，串列双圆柱后的旋涡已经变得规律。随折合流速变化，圆柱后尾流均为2S模式，如图5所示。除了在圆柱响应接近于零的区间，圆柱后旋涡均为两排；此外，旋涡之间的距离随折合流速增加，这与圆柱脱落频率的下降有关。

3.2 广折合流速响应机制(L*=1.1)

当间距比L*=1.1时，串列双圆柱的响应存在于一个较广的折合流速范围内(Ur=4.0～28.0)，且远大于单圆柱涡激振动对应的折合流速范围(Ur=4.0～8.5)。本节将深入讨论其背后原因，揭开此广折合流速响应的耦合机制。

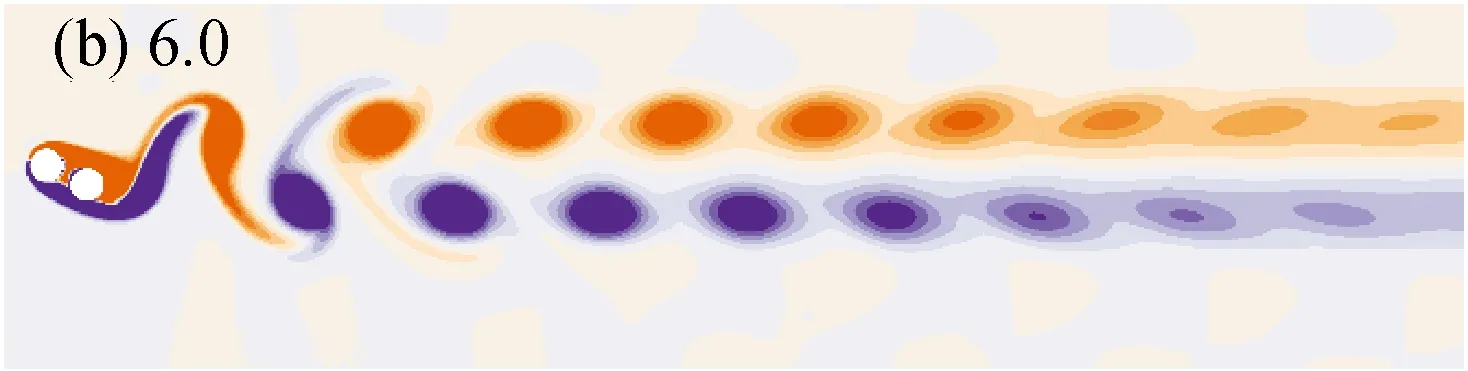
图4 间距比L*=1.3时，不同折合流速下串列双圆柱后的流场

Fig.4 Wake flow behind two tandem cylinders for different reduced velocities atL*=1.3

图5 间距比L*=1.5时，不同折合流速下串列双圆柱后的流场

Fig.5 Wake flow behind two tandem cylinders for different reduced velocities atL*=1.5

图6 串列双圆柱平衡位置差Δ1,2以及位移差均方根Δrms随折合流速变化情况

Fig.6 The difference of the equilibrium position (Δ1,2) and the r.m.s value of the difference of displacements (Δrms) between two tandem cylinders

当折合流速Ur≥8.5以后，两圆柱平衡位置差缓慢增加而两圆柱的响应也趋于达到最大值(Ur=9.0)，同时两圆柱之间的耦合作用也达到了最大。此后圆柱的响应随折合流速减小，一直到折合流速Ur≈12.0时到了谷值。进一步增加折合流速，两圆柱的响应又开始增加，并伴随着复杂的升力频率，如图7所示。此时圆柱的响应受到多频率成分的作用，串列双圆柱之间的耦合机制也相应地发生变化。由于平衡位置差逐渐增加，两圆柱之间的空隙也随之增加，如图2(f)所示。从上游圆柱脱落的旋涡可以完整地从下游圆柱的上侧通过，这不仅保证了旋涡脱落带给上游圆柱足够的动力，旋涡形成的低压区也会对下游圆柱的振动起到促进作用，这成为该阶段圆柱之间的新耦合机制，同时也保证了在大折合流速下串列双圆柱可以以较大的振幅振动。

图7 不同折合流速下串列双圆柱的升力频谱(L*=1.1)

Fig.7 The lift spectrum of two tandem cylinders for different reduced velocities atL*=1.1

当折合流速Ur≥28.0以后，两圆柱之间的平衡位置差已超过1.5D，这可能使得两圆柱的耦合作用不再那么强烈，两圆柱的响应也逐渐下降。当折合流速Ur=30.0时，受到下游圆柱的影响，上游圆柱下侧的旋涡不仅强度变小；上游圆柱也影响了下游圆柱上侧旋涡的充分发展，因此，两圆柱的响应均大幅下降,如图2(i)所示。

数字PCR只能同时分析两种荧光信号，选择较实时定量PCR局限，不能在单管中同时对多个位点进行分型；而在定量方面相较实时定量PCR准确度更高、检测阈值更低，可检测单个拷贝或单个目标分子，且在复杂的背景中或存在高浓度、高度同源序列的背景中检测出稀有的、单个碱基突变具有显著的优势。这主要是由于数字PCR将单分子的模板分散到每个小的反应体系中，从而每个反应体系只扩增单一模板，减少了模板分子之间的竞争或抑制作用，减少了等位基因脱扣或母源非特异性扩增的发生。

3.3 类尾流弛振机制(L*=1.2～1.3)

当间距比L*=1.2～1.3时，串列双圆柱的响应在大折合流速时随折合流速增加，圆柱的响应出现类似于高雷诺数下串列双圆柱中的尾流弛振现象。需要说明的是随间距比增加，该现象开始于更大的折合流速下。当串列双圆柱涡激振动进入该区间，圆柱的响应和升力变得不再规律，而是由多个频率成分组成。上游和下游圆柱的升力频率均相当混乱，除了相应的主导频率之外，其余各杂频也占据一定幅值，也会在响应和升力变化中起到相当的作用,如图8所示。因此，低雷诺数下串列双圆柱的类尾流弛振现象同样源自于两圆柱之间的不稳定相互作用。值得注意的是，这种不稳定作用来自于各不同的频率成分的共同作用，与Assi等对高雷诺数下串列双圆柱尾流弛振现象的机理并不一样，这是因为高雷诺数下串列双圆柱的升力只有一个低频主导[31]，其余频率并未起到关键的作用。此外，在高雷诺数下，旋涡的三维性也明显不同于低雷诺数下二维的尾流。

图8 不同折合流速下串列双圆柱的升力频谱(L*=1.2～1.3)

Fig.8 The lift spectrum of two tandem cylinders for different reduced velocities atL*=1.2—1.3

3.4 大振幅响应持续机制(L*=1.5)

当间距比L*=1.5时， 串列双圆柱的响应在折合流速Ur≥28.0以后不再变化，分别稳定在Yrms/D=0.35和Yrms/D=0.55上；此时上游圆柱的响应与单圆柱涡激振动最大振幅Yrms/D=0.40相当，而下游圆柱的响应比该最大值大37.5%。需要说明的是，进一步的数值模拟显示当折合流速Ur=50.0时，上游和下游圆柱的响应分别为Yrms/D=0.34和Yrms/D=0.54，与折合流速Ur=30.0时几乎一致。因此可以断定，大振幅响应可以持续到非常大的折合流速。本节将就该大振幅响应持续机制展开研究，分析如下：

当下游圆柱的响应向平衡位置运动的过程(从A点到C点)，上游圆柱脱落的旋涡恰好位于下游圆柱的下侧并产生低压区，形成的低压区会对下游圆柱的运动产生吸引作用，促进下游圆柱的振动,如图9所示。当下游圆柱运动到点B对应的位移时，上游圆柱上侧未分离的负剪切层出现在两圆柱的中间，随着上游圆柱向下运动，该剪切层将会推动附着在下游圆柱下侧的旋涡向下游移动，由于受到推动作用，下游圆柱上即将分离的剪切层速度变快(从点C到点D)，此时在下游圆柱的下侧产生更低的低压区，从而产生更大的升力。当下游圆柱回到最大负位移(点E所对应的位置)，圆柱周围的涡量场分布恰与点A时的情况反对称，相同的机制促进下游圆柱向上侧的大振幅响应。此为大振幅响应持续的机制之一。此外，在折合流速Ur≥28.0范围内，串列双圆柱的频率均较低且同值，如Ur=30.0时均为f1=f2=0.095和Ur=50.0时均为f1=f2=0.092。较低的频率保证了上游圆柱脱落旋涡产生的低压区可以有更长的时间来促进下游圆柱的运动，提供更多的动力。此为大振幅响应持续的机制之二。在两机制的共同作用下，串列双圆柱大振幅响应得以持续到更大的折合流速下。

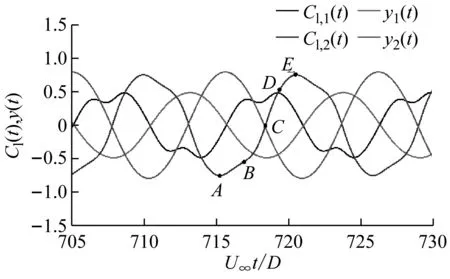
图9 不同时刻下串列双圆柱后的流场

Fig.9 Wake flow behind two tandem cylinders for different time instants

3.5 平衡位置跳跃现象(L*=1.1)

在间距比L*=1.1和折合流速Ur=15.0时，串列双圆柱涡激振动出现了一个平衡位置的间歇跳跃现象，如图10所示。需要说明的是在本文所研究的参数空间内，跳跃现象仅出现在该间距比和折合流速下。

图10 串列双圆柱的位移历时曲线(L*=1.1,Ur=15.0)

Fig.10 Time history of the displacements of two tandem cylinders atL*=1.5 andUr=15.0

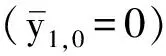
4 结 论

本文对小间距比(L*=1.1～1.5)下串列双圆柱涡激振动的尾流和圆柱之间的耦合机制进行了全面深入的研究，其中雷诺数为Re=100。对圆柱尾流的研究发现，在折合流速较小(Ur=3.0～4.0)时，由于圆柱的响应几乎为零，上游圆柱脱落的旋涡将两圆柱包裹在一起，并在下游形成经典的2S模式。随响应的增加，圆柱后的2S模式变成了并排的两列，且旋涡之间距离也随之增加。在间距比L*=1.1～1.3内，由于响应由多频率成分组成，不稳定的耦合区域存在于较大的折合流速下，此时圆柱后的尾流变得混乱。两种新的尾流模式出现在间距比L*=1.1和L*=1.2时，分别为T+S模式和P+S模式，前者仅出现在多圆柱的涡激振动中，后者曾出现在高雷诺数下单圆柱涡激振动中[32]；两种模式反映的是圆柱之间的耦合作用。当间距比L*=1.5时，圆柱后的尾流变得规律起来，均为2S模式。

对各间距比下的耦合作用研究发现，当间距比L*=1.1时，圆柱大振幅响应存在于一个较广的折合流速区间内Ur=4.0～28.0，而产生这种现象的原因为串列双圆柱之间平衡位置差的调和。正是圆柱平衡位置差的变化，才使得圆柱响应在折合流速Ur≥12.0以后又开始随折合流速增加，此时圆柱之间的耦合作用便不同于折合流速较小时(两圆柱的平衡位置均为初始位置)的情况。类尾流弛振现象出现在折合流速较大时的间距比L*=1.2～1.3下，而该现象的原因源自于多频率参与的不稳定的相互作用，其机制完全不同于高雷诺数下串列双圆柱涡激振动中的尾流弛振现象。当间距比L*=1.5时，大振幅响应一直持续到很大的折合流速，且保持响应幅值不变，该现象背后的机理有二：①上游圆柱脱落旋涡产生的低压区促进了下游圆柱的运动；②下游圆柱较低的频率保证了低压区提供足够长时间的推动力。

此外，在间距比L*=1.1和Ur=15.0时，一种串列双圆柱平衡位置的间歇跳跃现象出现，即两圆柱的平衡位置在正/负两个新平衡位置之间来回变化。与下侧平衡位置相比，上侧平衡位置更稳定，能存在更久的时间。