摇摆自复位高墩高阶效应研究
2018-12-21张育智
张育智
(西南交通大学 土木工程学院,成都 610031)
采用延性方法设计桥墩时,通过在桥墩与承台或(和)桥墩与主梁的连接部位进行塑性铰设计,使桥墩在大地震时在上述位置形成塑性铰,一方面塑性铰的出现会降低结构刚度,延长结构周期,从而可以减小输入到结构中的地震动能量;另一方面塑性铰的出现将消耗大量已经输入结构的地震动能量,减小结构整体的地震动响应。虽然延性设计能够实现“大震不倒”的性能要求,但由于塑性铰的形成,使结构发生了永久性的残余变形,导致了结构的损伤,这直接导致震后结构功能的恢复非常困难。由于经济和安全原因,大量按照延性方法设计的结构往往在震后被拆除而非修复,这在造成巨大经济损失的同时,给人民的震后生活带来了极大不便。
随着研究的逐步深入,研究者越来越清晰地意识到控制结构地震残余位移的重要性[1-5]。在20世纪90年代便有研究者提出了震后无损伤结构设计方法[6]。该方法的核心思想是将结构设计成具有摇摆自复位能力的结构。对于桥墩来说,摇摆自复位桥墩是指: 将桥墩与承台或(和)桥墩与主梁之间连续的钢筋断开,放松桥墩在上述部位受到的转角约束,在发生大地震时,桥墩能够在上述部位形成摇摆界面,利用桥墩的摇摆降低对桥墩抗弯能力的地震需求,使结构在大地震中仍能处于弹性工作状态,且在地震结束后,结构能够自动恢复至初始位置。震后无损伤结构设计的目的是: 结构的地震内力并非随地震动强度的增大而持续大幅增大,而是将结构的地震内力控制在一定范围内,这样就可以最大程度地消除地震动不确定性导致结构损伤的可能性,即使地震动强度比设计结构时所采用的地震动强度高,结构仍然不会在地震过程中发生损伤。
在地震过程中,根部形成塑性铰的剪力墙可以视为摇摆结构,在对摇摆剪力墙的研究过程中[7-10],研究者发现利用非线性时程计算得到的根部剪力比按照一阶模态分布的水平地震力作用下计算出的根部剪力大,前者约为后者的1.4~4倍;且结构将在除根部以外的其他位置形成第2个塑性铰,随着研究的深入,研究者认识到这是由于摇摆自复位结构的高阶效应导致的——虽然1阶模态效应在结构发生摇摆后便不会继续增大,但高阶模态效应可以在结构根部形成摇摆界面的边界条件下继续增大,这便是摇摆自复位结构中的高阶效应。
为了实现震后无损伤,必须对摇摆自复位结构高阶效应进行控制。为此,首先需要判断各阶模态对结构地震响应的贡献,从而确定需要控制哪些阶次的高阶效应。国内对摇摆自复位结构的研究起步较晚,对摇摆自复位结构高阶效应的研究尚未见报道。国外对摇摆自复位结构高阶效应的研究主要针对钢框架结构[11],尚未见针对摇摆自复位高墩高阶效应的相关研究,由于高桥墩的动力性能与钢框架有较大差别,有关钢框架的结果并不能直接用于高桥墩。因此,开展针对摇摆自复位高墩高阶效应的研究非常必要。
1 高阶模态贡献的计算方法
Wiebe[12]采用振型参与系数、各阶模态振型及加速度反应谱构造了反映各阶模态贡献的综合指标,对摇摆自复位框架的高阶振型贡献随着结构根部抗弯刚度变化的规律进行了研究,但该方法并不适用于对某一特定摇摆结构整个摇摆过程中各阶模态振型贡献的计算。Hasan等[13]利用模态分解法对四层摇摆自复位框架结构中各阶模态贡献进行了研究,由于概念清晰,便于理解,因此本文采用模态分解法对摇摆自复位高墩的各阶模态贡献进行分析。
模态分解法的思路是利用在线性系统中成立的模态分析方法来计算非线性摇摆自复位结构的各阶模态动力响应,因此模态分解法是一种近似方法。
(1) 各阶模态内力的计算。
结构各阶模态引起的结构内力,包括剪力和弯矩,可以根据对结构非线性时程计算得到的等效地震荷载进行模态分解而求得。根据结构动力学[14]模态分析的相关知识,首先引入非线性多自由度结构第n阶模态的等效地震静力{fe,n(t)}
{fe,n(t)}={sn}·αn(t)
(1)
式中:αn(t)为与线性结构中的伪加速度An(t)相对应的非线性系统中第n阶模态的伪加速度; {sn}为第n阶模态等效地震荷载的空间分布向量
{sn}=Γn·[m]{φn}
(2)
式中:Γn为振型参与系数; [m]为结构的质量矩阵; {φn}为结构的第n阶振型。
假定叠加原理对摇摆自复位结构仍然适用,则结构t时刻总的等效地震静力{fe(t)}等于t时刻各阶等效地震静力之和,即
(3)
利用振型的正交性,将式(3)左右两侧左乘{φn}T经整理得
(4)
式中:Mn为第n阶模态的广义质量。
具体求解方法及步骤:
步骤1根据非线性时程计算的结构剪力结果可以得到t时刻结构中各节点的等效地震静力{fe(t)},即由相邻单元根部剪力差组成的列向量;
步骤2由式(4)可以得到第n阶模态的伪加速度αn(t);
步骤3由式(1)计算第n阶模态的等效地震静力列向量{fe,n(t)};
步骤4由式(5)可求得t时刻第n阶模态对应的桥墩根部剪力Qn(t)
(5)
式中:fie,n(t)为t时刻i节点的等效地震静力;m为节点数;
步骤5由式(6)可得t时刻第n阶模态对应的桥墩墩底弯矩Mn(t)。
(6)
式中:hi为i节点到墩底的高度。
(2) 各阶模态位移的计算。
为计算各阶模态位移,需要引入与第n阶模态单自由线性系统位移响应Dn(t)相对应的第n阶模态单自由度非线性系统等效位移响应δn(t)。 则第n阶模态的位移向量{un(t)}可以表示为
{un(t)}=Γn·{φn}·δn(t)
(7)
利用叠加原理,结构总的位移向量可以表达为
(8)
利用振型的正交性,式(8)左右两侧左乘{φn}T, 经整理可得第n阶模态单自由度非线性系统的等效位移
(9)
在得到δn(t)之后, 根据式(7)便可以得到各个时刻各阶模态对应的结构位移。
2 高阶模态贡献的定量指标
在由上述模态分解法求出各阶模态对应的结构剪力、弯矩及位移之后,为了求解各阶模态对这些结构响应的贡献,必须给出描述各阶模态贡献的指标。以往采用的指标主要有3种。
(1) 第n阶模态响应绝对值最大值|rn(t)|max与总响应绝对值最大值|rtot(t)|max之比ID1, 第n阶模态贡献计算公式见式(10),各参数意义见图1。
(10)
(2) 总响应最大值对应时刻tm第n阶模态响应值rn(t)t=tm与总响应值rtot(t)t=tm之比ID2, 第n阶模态贡献计算公式见式(11), 各参数意义见图1。
(11)
(3) 第n阶模态响应时程曲线与时间轴围成面积与总响应时程曲线与时间轴围成面积之比ID3, 第n阶模态贡献计算公式见式(12)。 其中tt是整个地震动持续时间。
(12)
上述ID1和ID2都只能反映某个时间点各阶模态响应与总响应之间的比值关系,极易受到地震动随机性的影响,不利于较完整和准确地描述各阶模态对总响应的贡献。ID3将整个地震动过程作为一个整体进行考虑,未对结构发生摇摆与未发生摇摆进行区分。而摇摆自复位结构在发生摇摆之后,其动力性能会发生变化,从而导致各阶模态对总响应的贡献发生一定的变化,因此采用ID3评价摇摆自复位结构各阶模态对总响应的贡献也存在不足。

图1 摇摆点竖向位移,总响应及第n阶模态响应时程示意图Fig.1 Sketch of rocking point vertical displacement, total and the n th mode response
由于结构发生摇摆后其动力性能会发生变化,且摇摆过程中结构响应值通常较大,为了反映摇摆结构的这一特点,各阶模态贡献指标应能反映结构发生摇摆时段内各阶模态的贡献。为此,本文作者提出ID4,即摇摆幅度最大的时间段内(图1中t1时段),经归一化的各阶模态响应时程曲线与时间轴所围面积与总响应时程曲线与时间轴所围面积的比值,见图1中摇摆点最大竖向位移uv,max对应的阴影面积,第n阶模态贡献计算公式见式(13)。
(13)
3 计算模型介绍
本文针对某圆端形铁路桥摇摆自复位桥墩[15]进行计算分析。桥墩的几何尺寸如图2所示,空心墩身高56 m,实心墩身及扩大基础均高2 m,桥墩外壁坡度为1∶40,内壁坡度为1∶90。桥墩采用C30混凝土,上部结构的质量为7 190 kN,以集中质量形式施加在墩顶节点,桥墩扩大基础底面,即摇摆界面,传递的竖向荷载为36 357 kN。本模型无耗能装置及后张预应力,依靠重力提供自复位的恢复力。采用OpenSEES对桥墩顺桥向的地震动响应进行非线性时程分析,桥墩采用弹性梁柱单元进行模拟,摇摆模型采用夏修身等[16]提出的两弹簧模型,两弹簧间距即为墩底扩大基础顺桥向尺寸10 m。弹簧单元刚度取为2.1×108kN/m,采用瑞利阻尼,取前2阶模态的阻尼比均为5%。计算模型的示意图见图3。
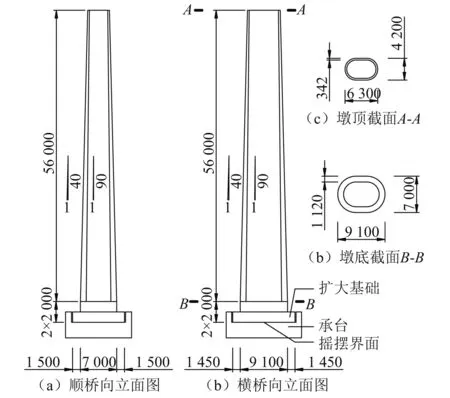
图2 桥墩尺寸图(单位: mm)Fig.2 Pier dimensions (unit: mm)
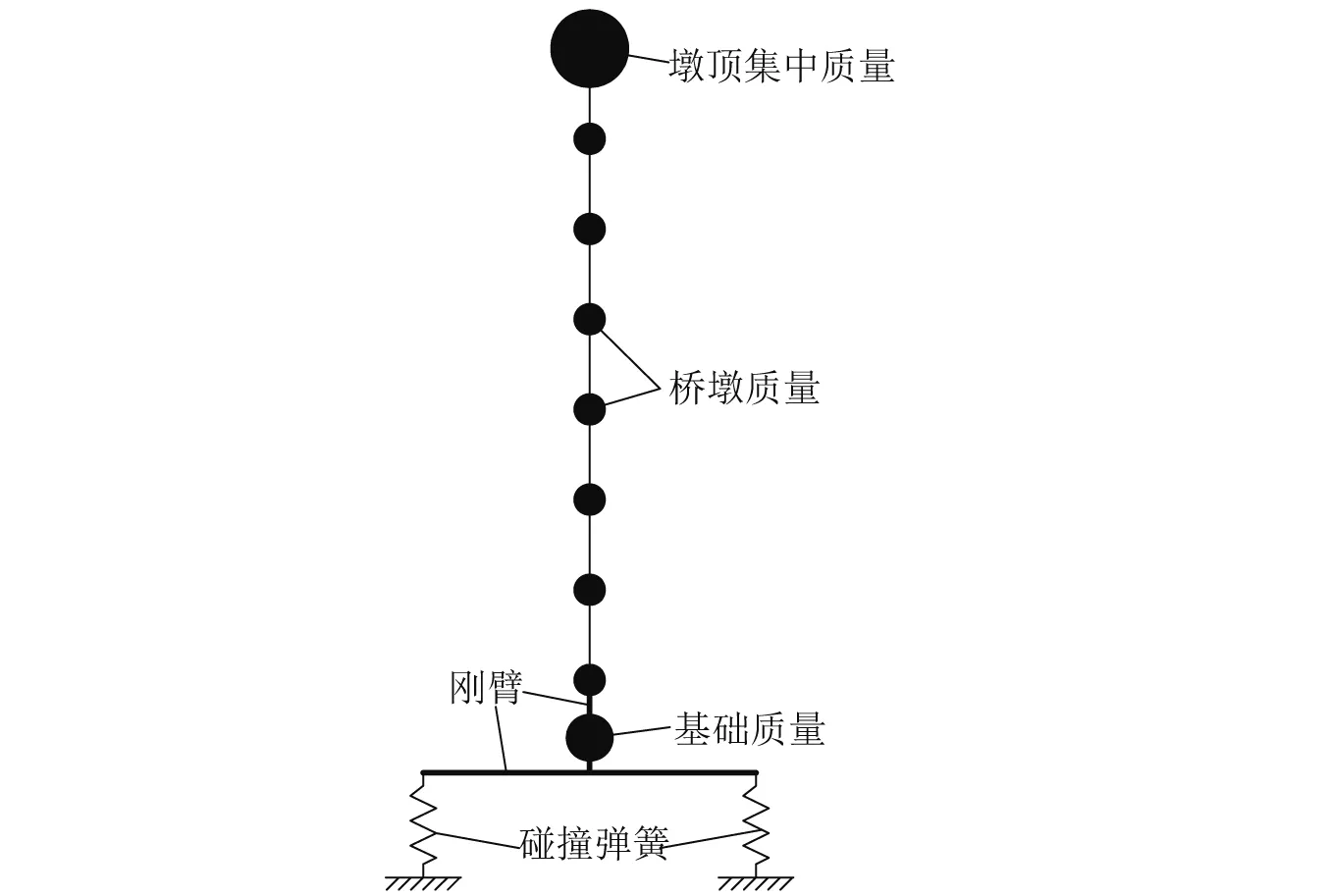
图3 有限元模型示意图Fig.3 Sketch of finite element model
4 地震动输入
为考虑地震动差异性的影响,从FEMA P695远场地震动系列中选取了7条D类场地的地震波作为输入,相关地震动记录的信息见表1。为了考虑地震动强度的影响,分别将地震动的峰值加速度调幅至0.2g,0.4g和0.6g。
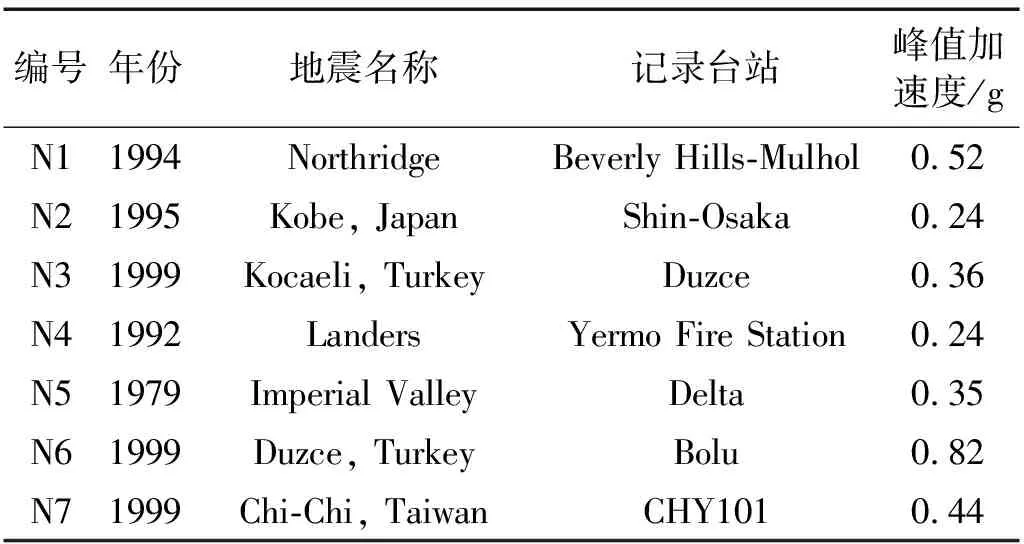
表1 地震动记录信息Tab.1 Information for ground motion records
5 计算结果
5.1 模态分解法计算结果
由于墩底剪力对高阶效应比较敏感,因此以墩底剪力为例,图4给出峰值加速度调幅至0.4g的N1地震动记录为输入时,结构前4阶模态与总响应的对比情况。
根据图4并结合表2给出的指标ID3和ID4计算得到的前4阶模态对墩底剪力的贡献百分比可见: 对于墩底剪力而言,前2阶模态对总响应的贡献均较大,二者之和占总响应的80%以上;第3阶模态对总响应的贡献仍达8.8%,而第4阶模态对墩底剪力的贡献便显著减小。

图4 墩底剪力总响应与前4阶模态对比Fig.4 Comparison of base shear for total and first four modes’ response
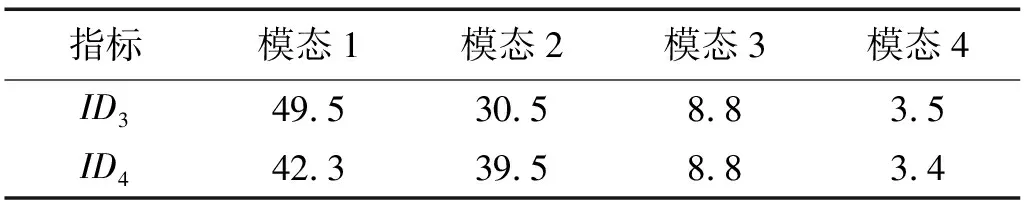
表2 前4阶模态对墩底剪力贡献比较Tab.2 Contribution comparison of base shear for first four modes%
5.2 各阶模态贡献计算结果
第2节中的指标ID1和ID2只是对结构响应最大值出现瞬时结构特性的反映,并不能充分反映各阶模态对总响应的贡献,在本研究中未采用上述2种指标。指标ID3是整个地震动作用时间范围内各阶模态对总响应的贡献的一种度量方法,但是未对摇摆自复位结构摇摆与否加以区分,不能反映出此类结构独有的特征。因为ID3和ID4都是归一化的指标便于比较,因此本节给出前3阶模态2种指标计算结果的对比。
5.2.1 墩底剪力计算结果
表3给出了不同地震动强度条件下2种指标计算的前3阶模态对墩底剪力贡献的平均值及变异系数。

表3 不同模态对墩底剪力的贡献对比Tab.3 Contribution comparison of base shear for different modes
由表3可得到以下规律:
(1) 随着地震动强度的增大,第1阶模态对墩底剪力的贡献逐渐减小,而第2阶和第3阶模态对墩底剪力的贡献逐渐增大,当地震动峰值加速度为0.6g时,2种指标得到的第2阶模态贡献分别已达到第1阶模态贡献的61%和97%,由此可见,高阶模态对墩底剪力贡献显著,在进行摇摆自复位结构抗剪设计时,必须充分考虑高阶效应的影响。
(2)ID3与ID4的差别随着地震动强度的增大而增大。产生上述差异的原因是ID3和ID4分别是针对整个地震动时长和最大摇摆阶段的评价,这种差异实际上反映出结构发生摇摆后各阶模态贡献与未发生摇摆时有一定的差异,这是摇摆结构特有的特性。当地震动峰值加速度为0.6g时,对比ID3与ID4的结果发现,第2阶模态的贡献分别达到第1阶模态贡献的61%和97%,采用ID3将大大低估第2阶模态的贡献。由此可见,对于摇摆自复位结构,ID4比ID3更适合评价结构响应较大的摇摆阶段高阶效应的贡献。
(3)ID3的变异系数比ID4的小。这是因为随着评价时长的缩短,计算结果越来越依赖于结构摇摆阶段的响应,而摇摆阶段的响应受地震动随机性的影响较大,因而当评价从整个地震动时长缩短到最大摇摆阶段时,各阶模态贡献变异系数就会增大。这实际上反映出摇摆阶段各阶模态贡献受地震动变异性影响较大,在实际分析时,应该采用多条地震动计算进行计算,并利用计算结果的统计值进行评价。
5.2.2 墩底弯矩计算结果
表4给出了不同地震动强度条件下2种指标计算的前3阶模态对墩底弯矩贡献的平均值及变异系数。
由表4可见,与表3反映出的规律类似,随着地震动强度的增大,第1阶模态对墩底弯矩的贡献逐渐减小,第2阶和第3阶的贡献有所增加;ID4比ID3更能反映出各阶模态贡献随地震动强度的变化规律。对摇摆自复位结构而言,高阶模态对墩底弯矩的贡献要小于对墩底剪力的贡献。
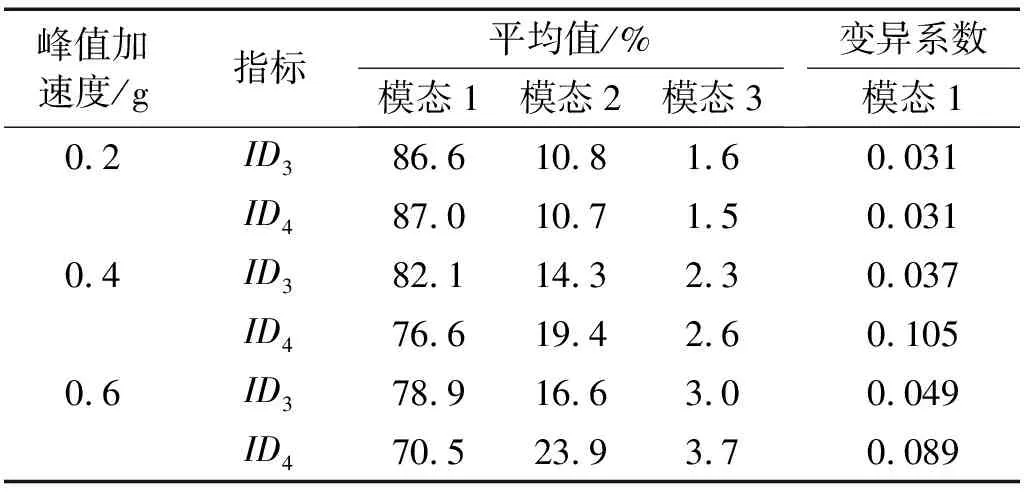
表4 不同模态对墩底弯矩的贡献对比Tab.4 Comparison of base moment for different modes
5.2.3 墩顶水平位移计算结果
表5给出了不同地震动强度条件下2种指标计算得到的前3阶模态对墩顶水平位移贡献的平均值及变异系数。

表5 不同模态对墩顶位移的贡献对比Tab.5 Comparison of pier top displacement for different modes
由表5可见,由于结构发生摇摆后,墩顶水平位移主要都是由结构绕摇摆点的刚体转动(即摇摆自复位结构摇摆状态下的第1阶模态)产生的,因此高阶模态对摇摆自复位桥墩墩顶水平位移的贡献很小,即使在地震动峰值加速度为0.6g的条件下,第1阶模态的贡献仍在90%左右。
6 结 论
(1) 应该采用能够反映结构摇摆阶段特性的指标ID4对摇摆自复位结构各阶模态贡献进行评价。
(2) 随着地震动强度的加大, 1阶模态的贡献逐渐减小,而2阶、3阶等高阶模态的贡献逐渐增大,在结构发生摇摆后,高阶模态的贡献比摇摆前大。
(3) 对于摇摆自复位高墩,墩底剪力对高阶效应最敏感,在分析时应考虑前3阶的影响;墩底弯矩对高阶效应较敏感,在分析时需考虑前2阶模态的影响;墩顶水平位移对高阶效应最不敏感,在分析时可只考虑1阶模态的影响。
(4) 摇摆自复位结构高阶效应控制的目标是对第2、第3阶模态的控制,且以第2阶模态的控制为重点。
致谢
本研究是在中央高校基本科研业务费专项资金的资助下完成的,在此表示感谢!
