伺服阀用超磁致伸缩致动器弓张结构设计与研究
2018-12-21郑佳伟何忠波李冬伟杨朝舒薛光明
郑佳伟, 何忠波, 李冬伟, 荣 策, 杨朝舒, 薛光明
(1.陆军工程大学 石家庄校区车辆与电气工程系,石家庄 050003;2.奥克兰大学 机械工程系,奥克兰 1010)
超磁致伸缩材料(Giant Magnetostrictive Material,GMM)是自稀土永磁、稀土磁光和稀土高温超导材料之后的又一种新型磁功能材料,能够较好地进行机械能-电磁能之间的可逆转换,其具有响应速度快、能量密度大、磁致伸缩应变大和居里温度高等一系列优良特性[1-4]。超磁致伸缩致动器(Giant Magnetostrictive Actuator,GMA)是一种基于GMM的微位移执行机构,可以精准、快速地输出纳米级的微位移。该致动器输出位移大、可靠性高、漂移量小,因而在流体机械、超精密加工、微马达及振动控制等工程领域具有巨大的应用前景[5-8]。
电液伺服阀控制精度高、响应速度快,是整个电液伺服控制系统的核心元件,其性能直接决定电液伺服系统的整体性能。对于GMA在电液伺服驱动机构方面的研究,国内外已经开展了许多。由于工作环境和空间受到制约,因而要求伺服阀体自身体积不宜过大,这就导致了所使用的GMM棒的长度受到限制。GMM的棒长受限直接导致整个GMA的输出位移量较小,因而无法控制大流量的液压元件,因此设计合适的GMA微位移放大机构对于拓展GMM在电液伺服领域应用范围具有十分重要的意义[9-12]。
目前,对于精密伺服驱动机构输出位移放大的方式主要有三种,包括液压放大式、悬臂梁放大式和柔性铰链放大式,其中柔性铰链放大式因具有高分辨率、无需润滑、结构简单等优点被广泛地应用在伺服驱动机构上[13-20]。王新华等[21]设计了一种基于柔性四连杆放大机构的超磁致伸缩直接力反馈伺服阀,能够实现输出力的自传感,并应用于水压传动与控制。曲兴田等[22]采用柔性铰链结构设计了一种压电叠堆泵,并测试了柔性铰链放大机构在不同电源激励下的动态响应、输出力与输出位移等特性;Karunanidhi等[23]设计了一种基于桥式放大机构的GMM喷嘴挡板阀,其稳态体积流量可达8 L/min。本文提出了一种基于三角放大原理的弓张式位移放大机构,该机构的连接部分采用柔性铰链结构,有效弥补了传统的三角放大机构输出线性度差、控制难、易疲劳破坏等缺点[24-26];同时为配合阀芯的输出方向要求,通过调整铰链的分布位置,使其垂直于固定端面向外侧输出。该放大机构与GMA紧密配合,整个机构体积精小、结构紧凑,同时具有频带宽、线性度好、放大比高等特点。文章分析了弓张式位移放大机构的放大倍数、静态特性和动态特性,制作了弓张放大式GMA样机并进行了试验研究。
1 弓张放大式GMA的总体构造及工作原理
弓张放大式超磁致伸缩致动器的总体结构示意图如图1所示,主要由弓张结构、预紧机构、GMM棒、偏置磁铁、激励线圈和冷却机构组成。弓张结构包括外侧的输出端、固定端和内侧与GMA相连接的两端,外侧固定端与阀体相连,用于固定弓张结构及内侧的GMA,输出端直接与阀芯相连,通过GMM棒产生的驱动力推动阀芯工作;预紧机构主要由碟簧和螺栓组成,能够为GMM棒提供适当的预紧力,从而提高GMA的输出特性;偏置磁铁产生较均匀的偏置磁场,用以消除GMM在高频振动时出现的倍频现象,同时可适量调节GMM内的磁场大小;激励线圈通电后产生励磁磁场,驱动GMM棒工作;冷却机构主要由油泵、油管及油液组成,其通过低温油液对整个GMA进行降温,以确保GMM棒工作在适宜温度环境中,使整个GMA具有稳定的输出状态。
整个弓张放大式GMA的工作过程为:当电流通过激励线圈时,线圈产生励磁磁场,GMM棒在偏置磁场和励磁磁场的作用下产生磁致伸缩微位移,并通过输出杆将微位移传递至弓张结构内侧两端,最终经弓张结构的外侧输出端放大后输出。考虑到阀体本身尺寸不宜过大,因此当偏置磁铁、激励线圈参数以及GMM棒尺寸确定的情况下,给激励线圈通入一定的电流时,GMA输出的位移即弓张结构的输入位移是一定的,因此弓张结构的位移放大比直接决定了整个机构输出位移的大小;同时弓张结构自身的动态特性也对整个机构性能具有较大影响。因此分析弓张结构的结构尺寸参数对位移放大比的影响, 获取参数最优解,建立弓张结构动力学模型,计算其固有频率,找出其产生结构谐振频率大小,能大幅提高伺服阀的整体性能。

1-后端盖;2-外壳;3-冷却液通道;4-线圈;5-线圈骨架;6-前端盖;7-弓张结构;8-偏置磁铁;9-冷却液入口;10-GMM棒;11-冷却液出口;12-碟簧;13-输出杆;14-连接固定螺钉(b) 弓张放大式GMA剖面图图1 弓张放大式GMA结构图Fig.1 Structure of GMA with bow-type
2 弓张结构位移放大倍数分析
2.1 理想位移放大倍数
将弓张结构的所有支点看作理想支点,所有支臂看作理想刚体,可计算弓张结构位移放大倍数的原理图如图2所示。

(a) 弓张结构

(b) 弓张结构多刚体模型图2 弓张结构原理图Fig.2 Schematic diagram of bow-type structure
由于整个机构具有高度对称性,因此只取其1/4作为研究对象,研究对象的理想模型图如图3所示。

图3 1/4理想模型图Fig.3 Quarter of ideal model
作A,B两点速度的垂线交于O点,采用速度瞬心法对放大机构的理想放大倍数r求解可表示为
(1)
式中:vA,vB为支点A,B点的速度,lx,ly分别为铰链A,B的水平距离和垂直距离;Δlx,Δly分别为在输入力作用下沿x,y方向产生的微小位移;θ为铰链A,B与水平线之间的夹角。
2.2 实际位移放大倍数
通过对弓张结构进行有限元仿真分析观察可知,实际上弓张结构在受力后发生弯曲变形的部位主要是柔性铰链A,B和输入两端的横梁,如图4所示。

图4 1/4受力变形图Fig.4 Quarter of force deformation
由此弓张结构的实际放大倍数R可表示为
(2)
式中:Δh,Δl分别为1/4放大机构水平位移和垂直位移;Δα为其弯曲旋转角度。
考虑到弓张结构的拉伸刚度及转角刚度,其铰链不能当作理想支点进行处理。将支臂AB近似为刚性杆,铰链近似为弹性梁,引入铰链的拉伸刚度和转角刚度后,其简化的弹性模型如图5。

图5 1/4弹性模型图Fig.5 Quarter of elastic model
根据静力平衡理论,易得出
(3)
令FA=FB=F,MA=MB=M,由于铰链A,B所受力的状态相同,因此二者弯曲旋转角度相同,均为Δα,图6显示了铰链A的受力弯曲状态。

图6 铰链受力弯曲图Fig.6 Force bending of flexure hinge
将铰链近似看作悬臂梁,基于弹性梁理论可求得
(4)
弓张结构两端的横梁可直接看作中点处施加集中力的简支梁,由材料力学知识可知简支梁中点处水平方向的相对位移为
(5)
式中:E为材料的弹性模量;b为弓张结构的厚度;l2为两端横梁长度;w1为支臂宽度;w2为两端横梁宽度。
相对于整个机构而言,GMM棒的伸长量很小,相应的旋转角Δα也很小,因此由刚性杆AB旋转所产生的弦长近似等价于其弧长,即可得
(6)
引入铰链拉伸刚度Kl和转角刚度Kθ的计算公式分别为
(7)
结合式(7),最终可得弓张结构的实际位移放大倍数为
(8)
式中:L为支臂AB长度;l,t分别为铰链的长度及厚度。
由式(8)可计算弓张结构各尺寸参数对其实际位移放大倍数的影响情况,如图7所示(考虑两个变化参数对R的影响时,其它参数为定值)。

图7 各尺寸参数对R的影响Fig.7 Effect of each size on R
由图(7)可得,随着t的减小,放大倍数先急剧减小,后缓慢减少,最后放大倍数趋近于零;随着ly的增大,放大倍数先急剧增大,到达最值后又急剧减小,后趋于一定值;w1,l,L这三个参数与放大倍数R近似呈线性关系,其中w1对R的影响最小;随着w2增大,R先急剧增大,到达一定值后,增速变缓。综合考虑弓张结构各参数对其放大倍数的影响,其中铰链厚度t及铰链间垂直距离ly对R影响最大,因此设计弓张结构时,主要考虑这两个尺寸参数。
2.3 位移放大倍数的有限元分析
使用COMSOL Multiphysics有限元仿真软件对弓张结构进行分析。弓张结构的主要尺寸参数设置为w1=7.72 mm,w2=9.80 mm,b=10.4 mm,l1=9.89 mm,l2=45.47 mm,l=4.11 mm,L=19.90 mm。分析时将横向位移输出端面的对应面固定约束,其它面均自由约束,在两侧轴向输入的内端面的中心局部面积上施加均布力。弓张结构的网格划分、相对位移及应力分布如图8所示。

图8 有限元分析图Fig.8 Finite element analysis
为获得弓张结构t和ly的最佳尺寸参数,改变t,ly参数值的大小,分别建立11个弓张结构模型,得到不同t,ly参数下的位移放大倍数值,并将计算式(1)、式(8)与有限元仿真的位移放大倍数进行比较,得到位移放大倍数随t,ly的变化情况,如图9所示。

(a) t对R的影响

(b) ly对R的影响图9 t,ly对R的影响Fig. 9 The impact of t, ly on R
由图9可以看出,当t值较小,ly值较大时,三种分析结果较为吻合。随着t值的增大,理想放大倍数保持不变,实际放大倍数缓慢减小,而FEM仿真放大倍数则减小地更快;随着ly值的增大,理想放大倍数急剧减小,实际放大倍数则是先增加到一定值后缓慢减小,FEM仿真放大倍数变化和实际放大倍数变化基本一致。相比之下,实际放大倍数比理想放大倍数更为接近FEM仿真值,原因是在于前者考虑了铰链A,B的变形,支臂AB的转动以及两侧横梁的变形,而理想条件下则完全未考虑各杆件的弹性变形。结合上图分析,综合考虑弓张结构自身强度要求及GMA整体尺寸限制,最终确定t=0.6 mm,ly=2.12 mm。
按照上文分析结果,重新建立弓张结构模型,通过施加0~800 N的均布力,经仿真得到弓张结构输入位移量和输出位移量,其变化关系如图10所示。

图10 输入与输出关系图Fig.10 Input and output diagram
根据以上有限元分析可知,弓张结构的输出位移随其输入位移的变化关系近似呈线性关系,由此可知在0~800 N均布力的作用下,放大机构的位移放大倍数及其静态等效刚度基本保持不变。经过计算,弓张结构的有限元分析放大倍数为10.18,理论分析结果为10.68,相对误差为4.6%。
3 弓张结构动力学建模
3.1 固有频率计算
将整个弓张结构视作单自由度系统,根据振动理论,其振动的固有频率表达式为
(9)
式中:Ke为弓张结构的等效刚度;Me为其等效质量。
计算弓张结构的势能时,将柔性铰链部分与支臂AB的等效刚度视为串联,由伪刚体模型法可得,弓张结构的弹性势能可表示为
(10)

弓张结构的动能由x,y方向的振动和绕z轴的转动动能组成,可以表示为
(11)
式中:ux=ΔL为弓张结构沿x方向的位移;uy=2Δly为沿y方向的位移。如图1所示,mk(k=2,3,4,5,6,7)满足m2=m3=m6=m7,m4=m5,Jk(k=2,3,6,7)代表各支臂mk的转动惯量
(12)
代入式(12),式(11)可化解为如下形式
(13)
将式(13)代入Lagrange方程
(14)
式中:qi为放大系统的广义坐标;U为系统的势能;Qi(t)为对应于广义坐标qi的除有势力以外的其他非有势力的广义力,n为系统的自由度数目,由式(14)可得
(15)
结合式(9)、式(13)、式(15),将m1=ρl1w1b,m2=ρLw2b,m4=ρl2w2b代入可得
(16)
式中:ρ为弓张结构的材料密度,取7 850 kg/m3;弹性模量E取215 MPa,将上述参数代入式(16),最终可得弓张结构的固有频率为105.9 Hz。
3.2 模态分析
模态分析可用来确定放大机构的固有频率和振型,能避免当外界激振频率接近放大机构的各阶固有频率时引起的结构谐振,从而影响其位移输出特性,同时可将机构的结构负载降低到最小,提高机构可靠性。利用COMSOL Multiphysics软件中的结构力学模块,对放大机构的模态进行分析,其前6阶模态及谐振频率如图11所示。
由图11中可知,弓张结构的二阶模态振型与其单自由度模型的振动方式相同,而其它阶次的振型会引起位移输出端的侧向振动,影响其输出精度。利用有限元仿真得到弓张结构的二阶振型的频率为115.7 Hz,对比动力学分析得到的固有频率105.9 Hz,两者间误差为8.4%,说明所建立的模型与有限元仿真基本吻合。

图11 弓张结构模态分析Fig.11 Model analysis of bow-type structure
4 试验验证
结合上文分析,制作了弓张放大式GMA试验样机,并搭建了测量弓张结构的输出位移及动态特性的测试系统。
4.1 硬件组成
弓张放大式GMA测试系统及连接关系如图12所示。系统包含的主要设备有:Rigol-DG1022U信号发生器,用于产生激励信号;GF800功率放大器,用于放大激励信号,驱动弓张放大式GMA工作;MicrotrakTM3-LTS-025-02激光位移传感器,精确测量位移大小;IT6932A可编程电压源,输出24 V恒定电压,给传感器供电;冷却机构,维持弓张放大式GMA工作温度恒定;pico-TA189电流钳,精确测量线圈电流;Rigol-DS1074Z数字示波器,采集试验数据。

图12 试验系统组成图Fig.12 Photo of experimental system
4.2 试验结果及分析
4.2.1 正弦激励试验
采用频率分别为30 Hz,40 Hz,50 Hz,60 Hz的正弦信号对弓张放大式GMA进行激励,并以1 A为梯度在1~5 A内逐渐改变输入电流的大小,通过激光位移传感器测量弓张结构的轴向、横向位移大小。试验过程中,对每个点进行10次测量,处理时,去掉数据中的最值,取剩余8次数据的均值,最终得到正弦波激励下弓张放大式GMA的位移响应曲线如图13所示。

(a) 轴向输入测试
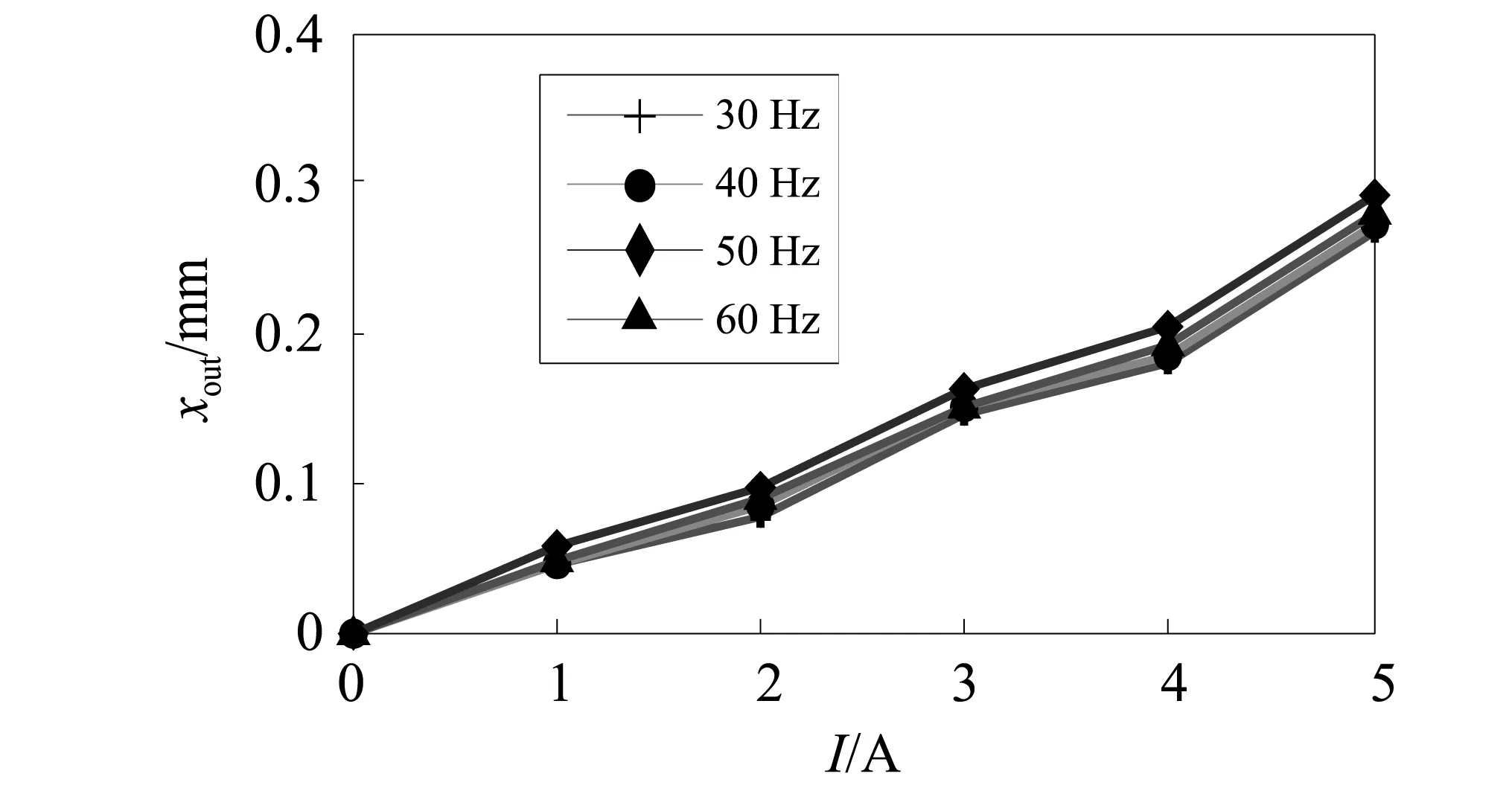
(b) 横向输出测试图13 位移测试曲线图Fig. 13 Curve of displacement test
由图13观察可知,弓张结构的轴向输入位移及横向输出位移随着电流的增大近似呈线性变化。将测试所得数据进行处理可得:当频率为30 Hz,40 Hz,60 Hz时,弓张放大式GMA的位移放大倍数在10.3~11.1波动,同理论结果相比,误差范围为3.5%~3.9%;当频率为50 Hz时,其位移放大倍数在11.5~12.0波动,同理论结果相比,误差范围为7.6%~12.3%。相比于频率为30 Hz,40 Hz,60 Hz时的测试结果而言,频率为50 Hz时,测量计算得到的位移放大倍数明显偏大,其原因可能是该频率值接近弓张结构的一阶固有频率,在该频率的激励下,弓张结构发生了侧向振动,导致横向输出位移的增大。
4.2.2 扫频特性分析
对弓张式GMA施加频率为0~200 Hz,幅值为3 A的正弦扫频信号,扫频时间长度设置为2 s,每个频率停留时间均等,其时域检测结果如图14所示。

图14 扫频试验结果图Fig.14 Result of sweep test
由所得试验数据分析可知,当频率在0~100 Hz内时,弓张结构的输出位移比较稳定,当响应频率达到108 Hz时,输出位移出现峰值,即该处激振频率与弓张结构的二阶固有频率相近,导致其出现结构谐振,使得其输出位移增大。
5 结 论
(1)设计了弓张放大式超磁致伸缩致动器,使得GMA在体积大小受限时也能输出较大位移,对于拓宽GMM在液压伺服领域的应用范围具有一定意义。
(2)利用理论力学、材料力学原理计算了弓张结构的理论、实际放大倍数,研究了弓张结构主要尺寸参数对其实际放大倍数的影响,最终确定了弓张结构具体尺寸参数,并用有限元仿真对其结果进行验证。
(3)利用材料力学及分析力学知识建立了弓张结构的动力学模型,计算出其固有频率大小,采用有限元仿真对其进行模态分析,确定了其前6阶固有频率,其中仿真得到的2阶固有频率与理论计算得到的固有频率相吻合。
(4)搭建了试验测试系统,对弓张放大式GMA样机进行了正弦激励试验和扫频特性试验,正弦激励试验得到弓张结构的位移放大倍数倍数在10.3~11.1波动,与理论结果相吻合,验证了计算的正确性;扫频特性试验得到样机波峰出现频率约在108 Hz,与理论值相符,其响应频宽可达到100 Hz,能够满足伺服阀输出特性要求。
