基于间接法识别的桥梁振型的损伤定位方法

贺文宇， 何 健， 任伟新

(合肥工业大学 土木与水利工程学院，合肥 230009)

基于振动的结构损伤识别技术是当前桥梁结构健康监测领域中的热点[1]。其基本原理是损伤会导致结构的自振频率、振型和模态阻尼比等参数发生改变，通过监测结构的动力响应，获取模态参数的改变可识别损伤的位置及程度[2]。尽管自振频率易于识别且精度较高，但其对结构损伤不敏感，且不同位置的损伤可能导致同样的频率改变。相反，振型不仅对结构损伤较为敏感，而且能提供损伤的位置信息。因此，基于振型的损伤识别方法被广泛的研究。

Pandey 等[3]用中心差分近似法计算出模态振型的改变来识别简支梁和悬臂梁的损伤位置。Zhu等[4]基于第1阶振型斜率变化，提出了识别受剪结构损伤的方法，并分别用8层框架的数值模拟和3层框架的试验对其进行了验证。上述方法的主要原理是：损伤位置处的模态振型曲率会发生显著变化，识别峰值点即可定位损伤。基于模态振型曲率变化的损伤定位法具有原理简单、结果直观、效率较高的优点，但其对高空间分辨率振型和基准振型的需求及中心差分法导致的低抗噪性，极大的限制了其应用。

通常为获取具有高空间分辨率的振型，需在桥梁结构上密集安装大量传感器，这不仅增加现场测试工作量，也将导致后续数据处理的成本过高。Yang等[5]提出了利用车辆响应识别桥梁模态参数的“间接法”。该方法只需在移动车辆上安装一个加速度传感器，就能识别高分辨率的桥梁振型。随后Yang等[6]进一步拓展了“间接法”，用希尔伯特变换识别简支梁的振型，同时探讨了各种因素如车速、路面粗糙度等对识别精度的影响。Qi等[7]提出了基于冲击激励下车辆动力响应的桥梁振型识别方法。Zhang等[8]从简谐荷载激励下移动车辆的响应中提取出振型的平方，并将其应用于梁式和板式结构的损伤识别。安宁[9]基于车桥耦合振动分析了车辆位移、速度、加速度响应对桥梁损伤的敏感性，通过灵敏度方法识别桥梁损伤。贾宝玉龙等[10-11]基于移动车辆响应提取出桥梁振型并应用改进的直接刚度法进行初步损伤识别。

在上述研究中，Yang等提出的方法具有坚实的理论基础，无需在车辆上施加附加激励，也无需除加速度传感器以外的多类型传感器。因此本文将基于“间接法”识别的高空间分辨率振型，采用区域振型曲率替代传统的振型曲率，多项式拟合的方法估计出未损桥梁的振型信息来定位桥梁损伤。数值算例探讨了测试噪声、路面粗糙度等对损伤定位精度的影响。

1 振型的间接识别方法

具有较高空间分辨率的振型是获得精确的损伤定位结果的重要前提。通常需在桥梁结构上密集安装大量传感器，这不仅增加现场测试工作量，也将导致后续数据处理的成本过高。为此本节将简要介绍通过加速度传感器获取的移动车辆响应，识别无损桥梁振型的基本原理，并通过数值算例检验其损伤桥梁振型的识别效果。

采用图1所示的移动车辆-简支梁模型进行移动车辆响应的简化分析，其中桥梁物理参数为：桥长L，单位长度质量m*，抗弯刚度EI，密度ρ，截面积A。移动车辆简化为一个弹簧质量块m，支撑于刚度为kv，阻尼为cv的弹簧上，车速为1 m/s。理论推导过程中不计路面粗糙度及桥梁阻尼。采用弹性假定和振型叠加法，可求得移动车辆的加速度响应为

(1)

式中：A1,n，A2,n，A3,n，A4,n和A5,n为与车辆移动速度v、车辆质量mv、桥梁自身频率wb,n、车辆频率wv和振动阶数n相关的系数。

图1 移动车辆-简支梁模型Fig.1 Moving vehicle-simply-supported beam model

(2a)

(2b)

(3a)

式中：RBn(t)为一窄带时间序列，其希尔伯特变换对为

(3b)

综合式(3a)和式(3b)可以得到第n阶桥梁振型的绝对值|φn(x)|

(4)

式中：A(t)为RBn(t) 的瞬时幅值

(5a)

(5b)

根据式(4)，可采用“间接法”识别桥梁的模态振型，主要包含以下4个步骤：①通过传感器测得车辆的加速度响应；②识别桥梁自振频率wb,n，并将与其对应的桥频响应部分RBn(t) 从车辆响应中分离；③用希尔伯特变换计算RBn(t) 的瞬时幅值；④应用瞬时幅值重构桥梁振型(其正负号可根据经验判断)。由于车辆可以经过桥面的任意点，因此通过间接法识别的桥梁振型可以具有非常高的空间分辨率。

Yang等通过数值算例证明了间接法能有效识别未损桥梁的模态振型。由于本文的目标是定位桥梁损伤，需探讨该方法是否能有效识别损伤桥梁振型。采用有限元法建立图1所示的移动车辆-简支梁模型，梁单元为两结点平面欧拉梁单元，不计剪切变形，结点位移包括挠度和转角。目前常选用以下三种模型对车辆进行模拟：整车模型、半车模型、单轮模型。依照简化原则，本文采用单轮单自由度模型分析车辆匀速过桥时的加速度响应[12]，假设弹簧不脱离梁体，不考虑阻尼和路面粗糙度。模型的几何、材料及截面参数分别为：桥长L=24 m , 弹性模量E=27.5 GPa,单位长度质量m*=1 000 kg/m, 惯性矩I=0.175 m4。桥梁共划分为24个梁单元，单元8和单元13承受20%的损伤 (刚度折减)。车辆参数为：车重mv=1 000 kg, 弹簧刚度kv=170 kN/m，车速v=1 m/s。

依照“间接法”识别桥梁的模态振型的4个步骤，识别出损伤桥梁的前2阶振型。其最大值归一化结果如图2所示。可以看出，“间接法”仍能有效识别损伤桥梁的模态振型，且识别的振型具有较高的空间分辨率。

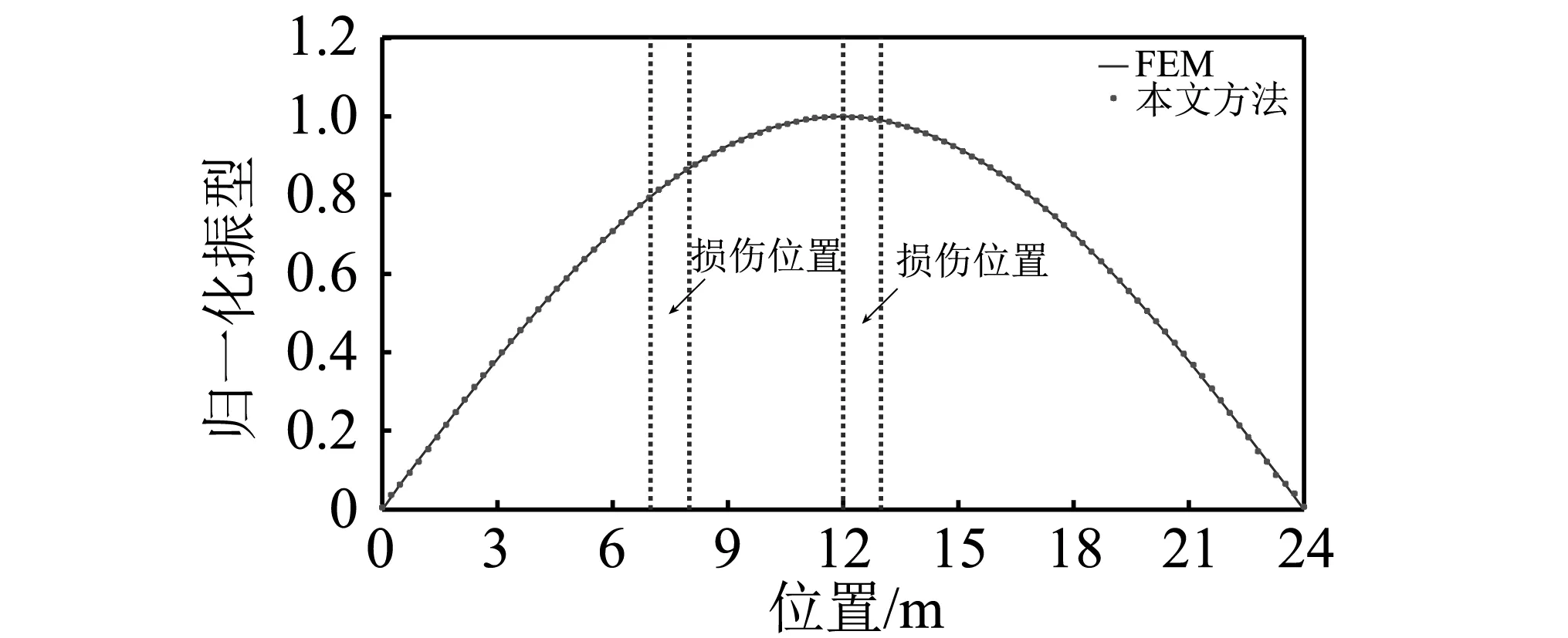
(a)第1阶振型

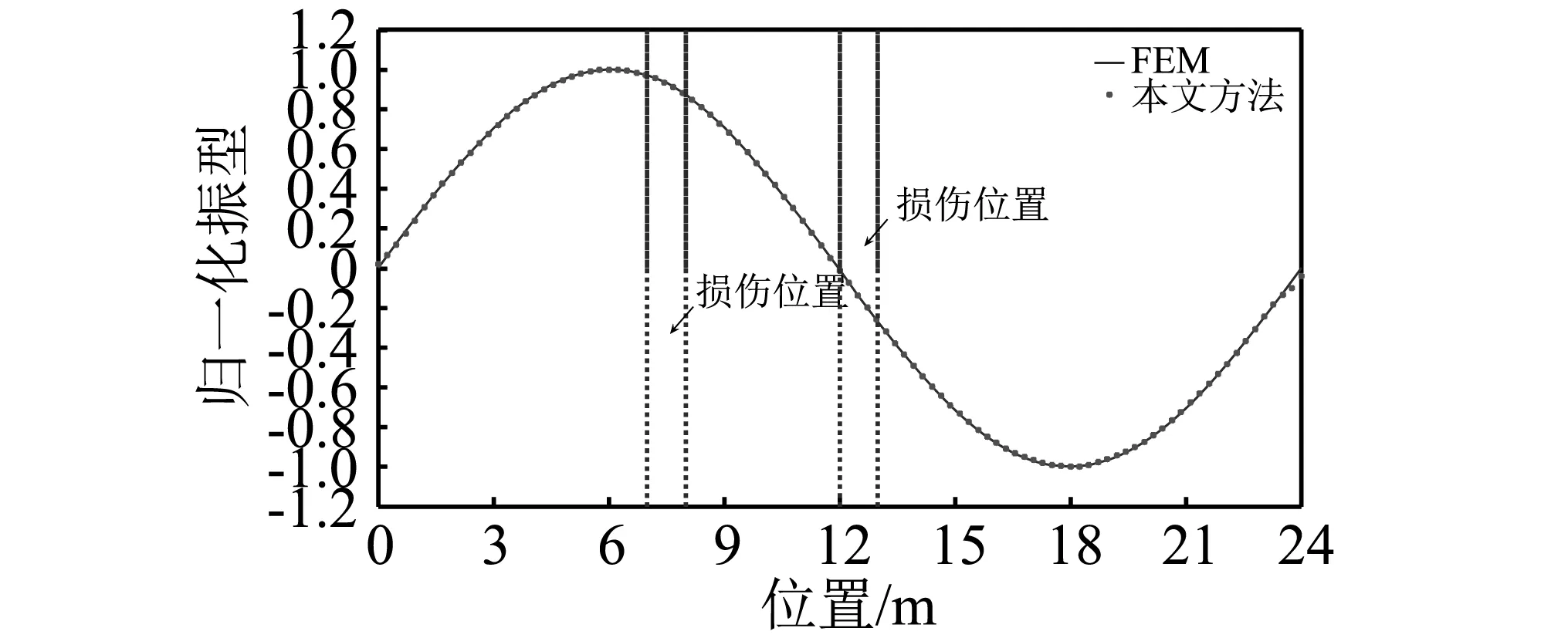
(b)第2阶振型图2 间接法识别的损伤梁振型Fig.2 Mode shapes of the damagedbeam identified by indirect method

2 损伤定位方法

基于模态振型曲率变化的损伤定位法具有原理简单、结果直观、效率较高的优点，但其对高空间分辨率和参照振型的需求及中心差分法导致的低抗噪性，极大的限制了其应用。本节将基于“间接法”识别的高空间分辨率振型，采用区域振型曲率替代传统的振型曲率，多项式拟合的方法估计未损桥梁的振型信息，进而定义损伤定位指标。

考虑到振动测试中，振型识别的精度随振型阶数的升高而降低，本文仅采用第1阶振型进行损伤定位。假设损伤桥梁识别出的第1阶振型为φd(x) ，将其等分为N段，桥梁因此也分成N个区域，如图3所示。振型的第i段与桥梁的第i个区域所围成的面积可通过式(6)计算

(6)

式中：xL,xR分别为第i个区域的左右边界；上标d为桥梁处于损伤状况。

损伤状况下的区域振型曲率可定义为

(7)

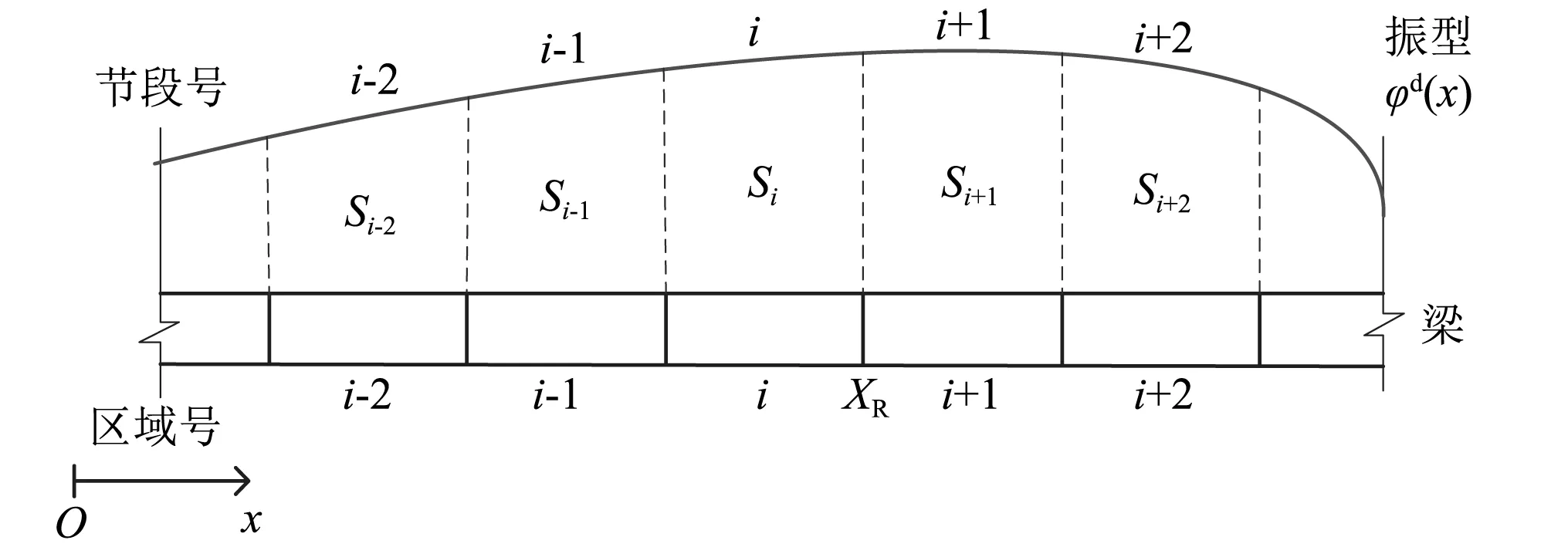
图3 振型与桥梁的分段Fig.3 Division of the mode shape and beam

考虑到希尔伯特黄变换的边界效应，将第1个和最后1个区域的值设置为0。RMSC类似于常用的中心差分法[13]，但与其只用单点数据不同的是，RMSC整合了区域中全部点的数据，因而具有较好的抗噪性能。

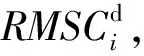
基于损伤前后的区域振型曲率的差值建立如下损伤定位指标DLI(Damage Localization Index)

(8)

3 数值验证

本节通过数值模拟的方法研究前文所提出的损伤指标DLI在不同损伤工况下简支梁的损伤定位的可行性。简支梁及移动车辆的相关参数同第2节，共设置24个区域，车速为1 m/s。损伤区域的位置及损伤程度如表1所示。

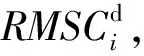
表1 数值模拟中的损伤工况Tab.1 Damage scenarios considered in numerical study

工况1中简支梁在区域[7 m, 8 m] (单元8)处有15%的损伤。工况2中简支梁在区域 [5 m, 6 m] (单元6)和区域[15 m, 16 m] (单元16)均存在 20% 的损伤。图4显示了用三次多项式拟合的未损伤状态RMSCu与理论RMSCu的对比，结果表明拟合值与理论值接近，拟合结果可以接受。图5(a)和图5(b)分别显示了相应的损伤定位结果。图5(a)中，单元8的DLI值远大于其他区域，因此该区域被识别为损伤位置。与之相似，工况2中的两处损伤均能识别出来。以上结果表明，本文提出的DLI能有效定位简支梁的损伤。

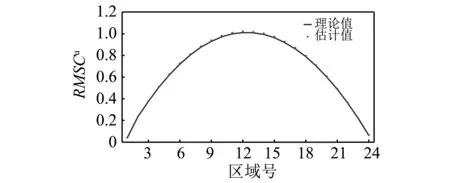
图4 拟合结果对比Fig.4 Comparison of fitting results

(a)单损伤

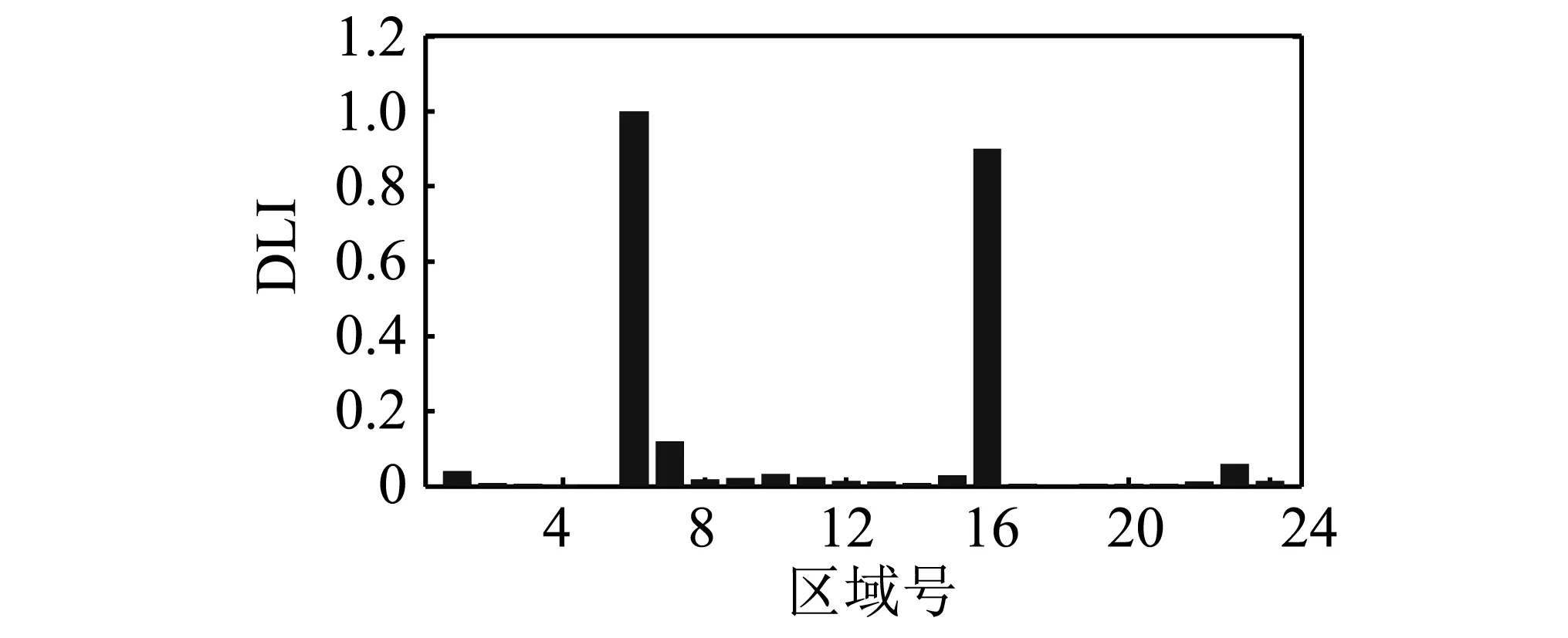
(b)双损伤图5 损伤定位结果Fig.5 Damage localization results

4 讨 论

4.1 测量噪声

在实际的振动测试中，测得的加速度响应将不可避免受到噪声的影响。鉴于此，在数值模拟过程中对加速度响应施加3%高斯白噪声

a=acal+3%Tnoise×σ(acal)

(9)

式中：a为包含噪声的加速度响应；Tnoise为服从标准正态分布的随机序列；acal为原始加速度响应；σ(acal)为原始加速度响应的标准差。

图6显示了有、无噪声条件下工况2的损伤定位结果。可见，尽管噪声导致了DLI值发生了变动，但损伤定位结果仍具有较高的精度。这主要是因为DLI由RMSC计算而得，而RMSC使用了整个区域所有点的数据，较中心差分法使用单点数据相比具有更好的抗噪性能。

图6 噪声对损伤定位结果的影响Fig.6 Noise effects on damage localization results

4.2 路面粗糙度

在众多影响因素中，路面粗糙度对基于移动荷载的桥梁健康监测方法影响最大。路面粗糙度r(x)为平稳高斯随机分布，根据功率谱密度函数用三角级数叠加法生成，如式(10)所示[14]

(10)

式中：di为余弦波增幅值；ns,i为在上下截止频率区间中以Δn为间隔的第i个空间频率；θi为随机相位角，在[0, 2π]服从随机分布。

路面粗糙度共分为8级，A级路面最平顺，H级路面最粗糙。为降低粗糙度的影响，Keenahan等[15]提出了利用两相连车轴过桥的方法。在本节中，也将采取该方法识别桥梁振型。如图7所示，两辆具有相同参数的车辆保持间距h，以相同且恒定车速v在桥梁上行驶。路面模拟为A级路面，如图8所示。

图7 两移动车辆过简支梁计算模型Fig.7 A simply-supported beam subjected to dual moving vehicles

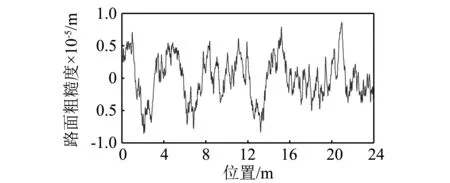
图8 路面粗糙度模拟Fig.8 Simulated rough roughness

两车的加速度响应分别为a1(x)和a2(x)，二者均受到路面粗糙度的影响。将二车在相同位置加速度响应的差值作为车辆的加速度响应，并应用此响应进行后续的损伤定位。图9所示的定位结果表明，当路面粗糙度等级为A时，损伤位置能被正确识别。但当路面粗糙度等级为B或C时，数值结果表明应用本文方法无法识别出损伤位置。

图9 路面粗糙度对损伤定位结果的影响Fig.9 Road roughness effects on damage localization results

5 结 论

针对基于模态振型曲率变化的损伤定位法需要高空间分辨率和参照振型以及低抗噪性的缺点，本文提出了一种基于间接法识别的桥梁振型的损伤定位指标。主要进行了如下工作：

(1)基于移动车辆的加速度响应，采用希尔伯特变换识别高空间分辨率的损伤梁振型。

(2)采用区域振型曲率替代传统的振型曲率，多项式拟合估计未损桥梁的振型信息，综合有损与无损的区域振型曲率定义损伤定位指标。

(3)通过数值算例验证了所提出指标的有效性，并探讨了测试噪声、路面粗糙度等对损伤定位精度的影响。

本文所提出损伤定位方法充分利用了间接法识别振型效率高、空间分辨率高的优点，且不需要未损伤桥梁的参考振型，抗噪性能好，具有一定的应用前景，后续将进一步通过实验室试验验证该方法的有效性。