杂波与色噪声条件下弹载雷达波形设计*

郑家毅,翁木云,何 丽,李 伟

(1 空军工程大学信息与导航学院,西安 710077;2 空军电磁频谱管理中心,北京 100800)

0 引言

随着科技水平的进步,导弹目标向更小体积,更轻重量,更快速度发展[1],这就要求弹载雷达具有更高制导精度,而弹载雷达对目标参数估计性能是制约导弹制导精度的关键因素之一。基于认知理论,从优化弹载雷达发射波形入手可有效提升弹载雷达对目标的参数估计能力,为提升导弹对目标检测性能奠定基础[2-3]。

围绕雷达波形优化设计,Bell[4]首次提出了基于互信息量(MI)准则的雷达波形设计方法;文献[5-6]综述了认知雷达关键技术及目标检测的最优波形设计方法;文献[7]讨论了MIMO雷达在MI和MMSE两种准则下的波形设计,并指出在相同发射功率约束下,以这两种准则优化波形能得到相同的效果;针对杂波、噪声条件下雷达波形设计问题,文献[8]利用信噪比(SNR)和互信息准则(MI)研究了信号相关干扰条件下针对确定和随机扩展目标的波形优化问题;文献[9]研究了色噪声条件下基于MI和MMSE准则的波形优化,并指出波形优化结果与目标特征向量和色噪声特征向量有关;文献[10]研究了基于MI准则的MIMO雷达波形设计方法,并给出了目标、杂波特征向量与噪声特征向量间的匹配顺序。虽然文献[8-10]等为杂波、噪声条件下雷达波形优化提供了很多有价值的方法,且优化效果良好,但由于前述研究仅限于目标信息已知的波形优化和优化效果分析,且大多适用于MIMO雷达,前述研究难以应用于采用单天线的弹载雷达上。

针对上述问题,文中提出了杂波与色杂声条件下基于线性最小均方误差准则(LMSE)的弹载雷达波形设计方法。该方法通过理论分析和推导,在弹载雷达信号发射功率限制下,利用注水定理分配信号频域能量,求解出优化波形频域能量分布具体表达式,从而提高弹载雷达对目标参数估计及检测性能。

1 弹载雷达制导信号模型

弹载雷达回波模型如图1所示。雷达发射信号s(t)能量有限,观测时间为[0,T],带宽为W,其傅里叶变换为S(f);h(t)为某持续时间有限的随机扩展目标,傅里叶变换为H(f),与s(t)卷积得到目标散射回波z(t),其傅里叶变换为Z(f);n(t)为高斯色噪声,均值为0,傅里叶变换为N(f),功率谱密度为Snn(f);c(t)为杂波冲击响应,采用零均值高斯随机过程描述,傅里叶变换为C(f),功率谱密度为Scc(f),与信号s(t)卷积得到杂波d(t),其傅里叶变换为D(f)。h(t)、c(t)、n(t)相互间统计独立;y(t)为弹载雷达接收数据,对应的傅里叶变换为Y(f)。

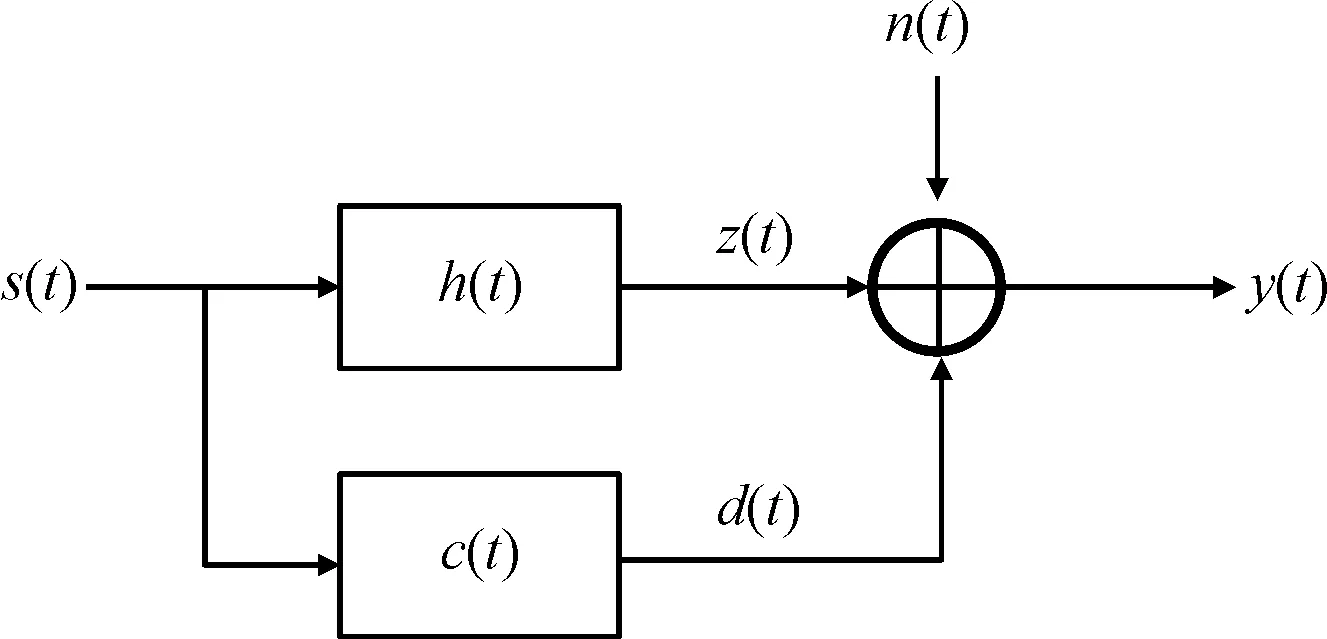
图1 雷达回波模型

时域信号模型为:

y(t)=s(t)*h(t)+s(t)*c(t)+n(t)

(1)

频域信号模型为:

Y=SH+SC+N

(2)

h(t)表征某随机目标,持续时间为Th,其脉冲响应均值为0,平均能量为:

(3)

(4)

E[|z(t)|2]=E[|s(t)*h(t)|2]

(5)

值得注意的是,E[|h(t)|2]可被看作是一个平稳随机过程与一个矩形窗相乘得到,而E[|z(t)|2]是由一个时间有限的随机脉冲响应与一个时间有限的波形的卷积得到的,因此,E[|z(t)|2]在[0,T+Th]内是非平稳的,不能用平均功率去描述,因此利用能量谱方差来描述E[|z(t)|2]:

(6)

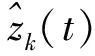
(7)

(8)

同理,杂波采样点方差为:

(9)

εN(Fk)=Snn(f)TΔf

(10)

采样点方差为:

(11)

2 基于线性最小均方误差准则(LMSE)的波形优化算法

将认知理论应用于弹载雷达并根据某种特定准则设计最优波形可有效提升弹载雷达检测[11-12]、识别及跟踪等性能。目前波形设计大多在目标信息已知的条件下开展研究,而弹载雷达刚开机时往往不具备充足的目标信息,因此提出一种针对目标最优估计波形设计方法是必要的。以目标参数估计值与真实值间线性最小均方误差[13]为准则(LMSE)来优化波形能够对目频率响应进行贝叶斯估计,且该估计方法仅需目标与观测值的前二阶矩统计知识,在实际工作中容易满足,所以得到广泛应用。根据图1回波模型,采样点线性最小均方误差估计子表达式为:

(12)

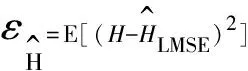
由于H与N为相互独立且不依赖于发射信号的零均值高斯随机变量,则有

(13)

上式对a求导并令其为0得:

E[2a-2H+bY]=0

(14)

故a=0。

对b求导并令其为零得:

E[2bY2-2HY]=0

(15)

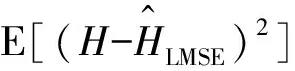
(16)

在2ΔfT个采样点上的总均方误差为:

(17)

当Δf→0时,上式可利用积分得到线性均方误差:

(18)

因此波形优化问题可转化为以雷达发射机能量为限制,求目标估计误差最小值问题:

(19)

利用拉格朗日乘子法:

(20)

式中λ为拉格朗日乘子,对式(20)关于|S(f)|2求偏导,令其结果为0,解得弹载雷达发射波形能量谱为:

(21)

(22)

令

(23)

(24)

(25)

(26)

考虑到发射信号能量谱非负,优化后信号能量谱可表示为:

(27)

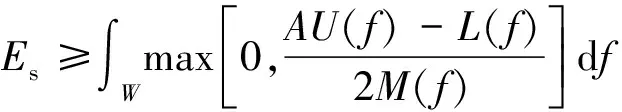
3 仿真分析

仿真试验中,设弹载雷达发射信号载频为fc=35 GHz,带宽为W=10 MHz,弹载雷达观测时间为1 ms,雷达接收机端采样率为fs=20 MHz,根据多点散射模型产生目标冲击响应,杂波、色噪声均为零均值高斯随机过程,弹载雷达初始发射信号为线性调频信号,初始发射功率为P=10 W。

3.1 杂波色噪声条件下波形优化

图2、图3展示了目标、杂波及色噪声功率谱密度,最终优化结果如图4所示。

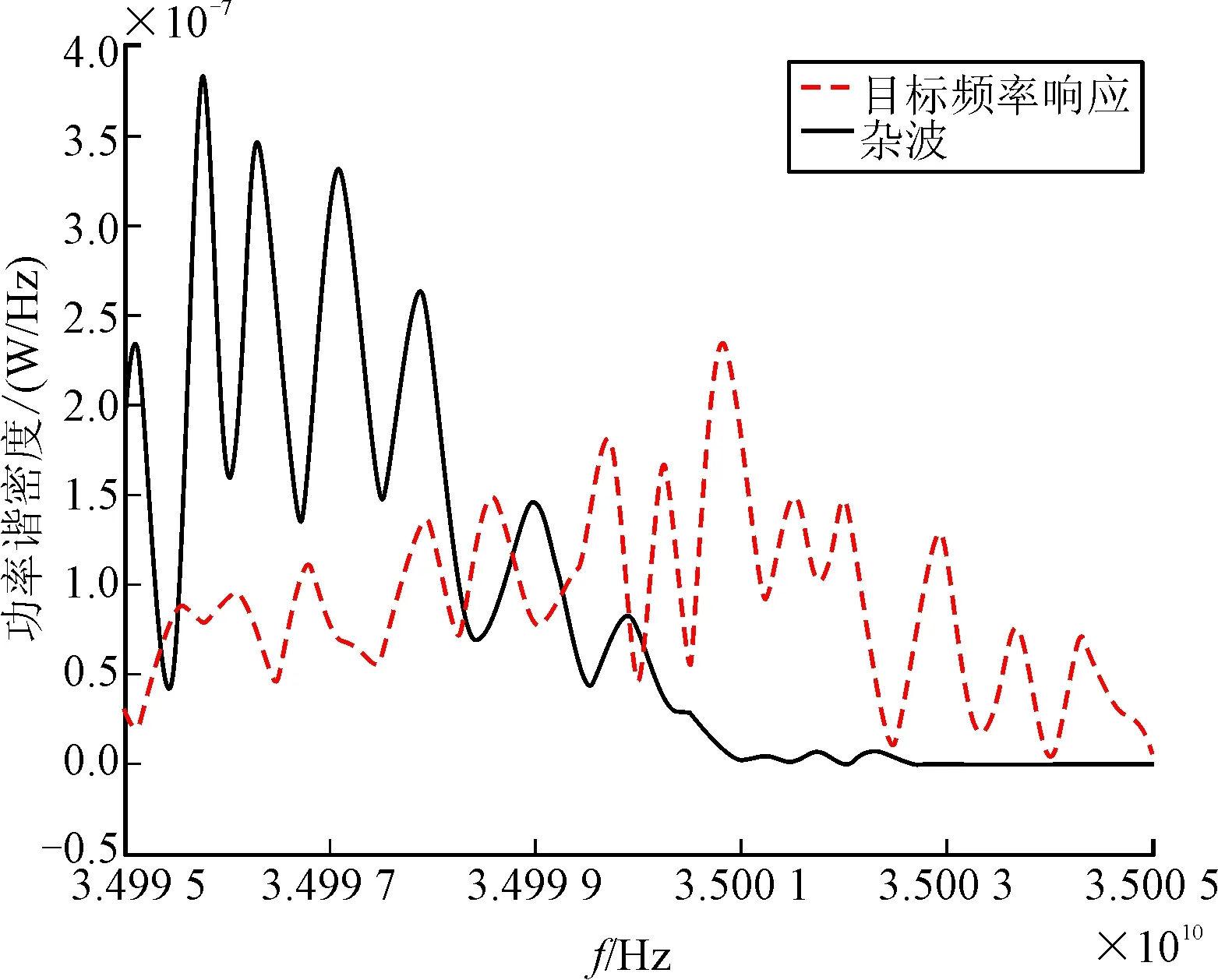
图2 目标及杂波功率谱密度

图3 色噪声功率谱

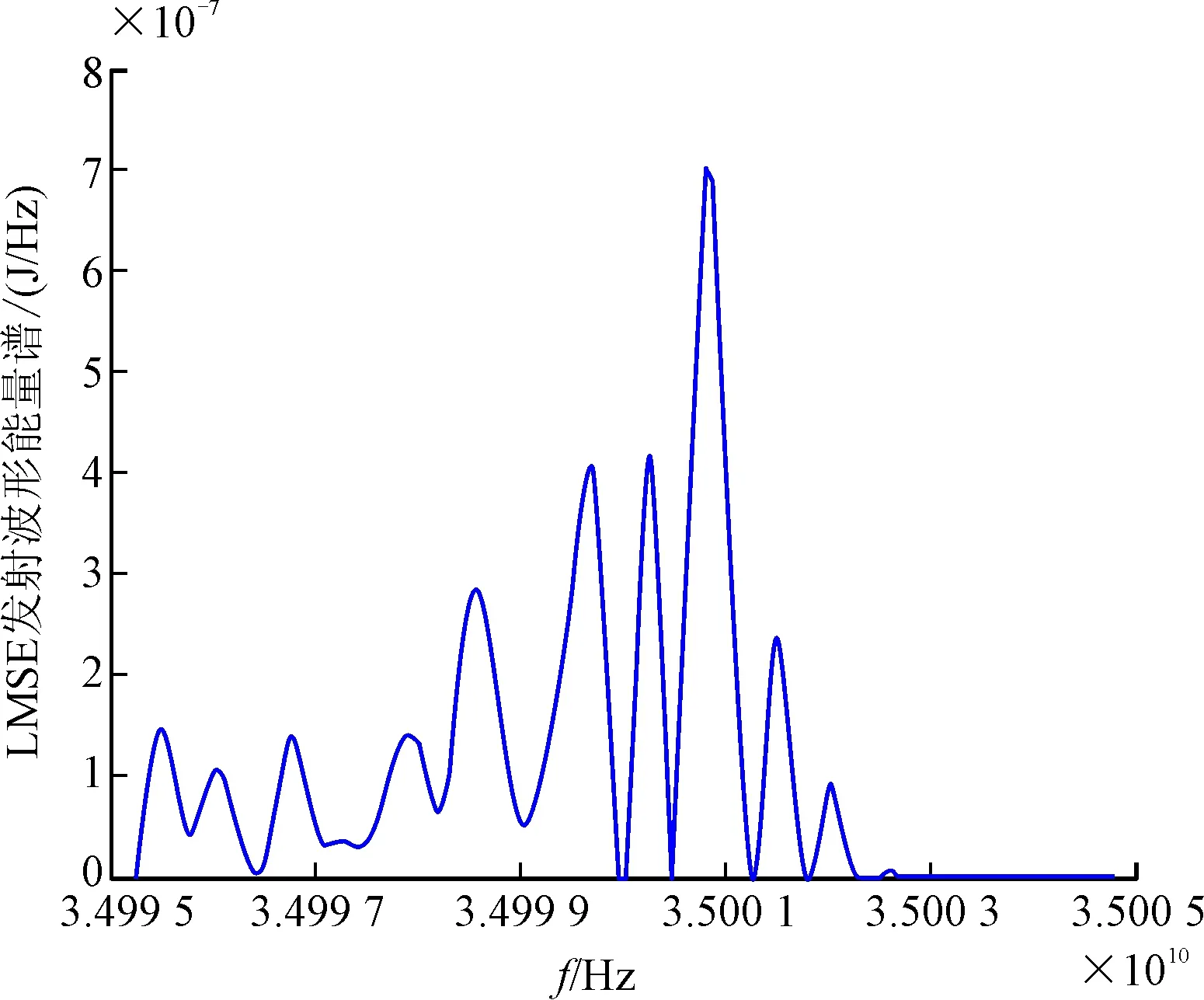
图4 优化信号能量谱

由图4可以看出,优化后的波形主要将能量分配在目标频率响应相对较大且杂波、色噪声相对较小的频段内,而在杂波、色噪声较大的频段处,发射信号能量分配较少甚至不分配能量。由前文分析可知,在杂波,色噪声较强处,目标频率响应真值与估计值间误差较大,发射信号在该处分配较少的能量会降低总体均方误差,该仿真结果与理论分析一致。

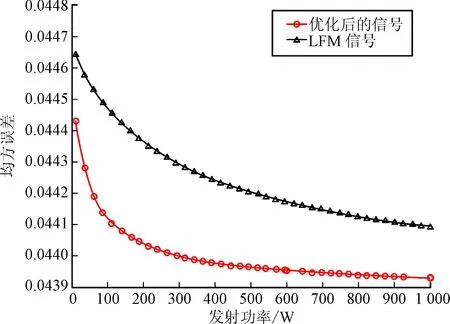
图5 发射功率对均方误差的影响

弹载雷达的参数估计性能往往受到信号发射功率限制。如图5所示,随着弹载雷达信号发射功率的增大,均方误差逐渐减小,最后趋于稳定。当发射功率较小时,优化前后弹载雷达估计目标频率响应的均方误差相差较小,这是由于此时目标回波与色噪声、杂波相比较小,目标频率响应难以估计;随着发射功率的提升,优化前后均方误差的差值逐渐增大,此时目标回波增强,且优化后的发射信号能够自适应的调整发射信号能量谱密度,减小总体均方误差,而LFM信号没有利用环境信息;当发射功率足够大时,色噪声相比目标回波较小,对估计误差的影响可以忽略不计,优化前后性能差异逐渐缩小,因此总估计误差趋于一个定值,即

该结论与图5的仿真结果一致。综上所述,相比优化前信号,以LMSE准则设计弹载雷达波形能够更精确的估计目标频率响应。

3.2 波形优化前后检测性能分析

以LMSE为准则优化的发射信号相比LFM信号不仅能提升弹载雷达对目标频率响应的估计精度,同时可有效改善杂波及色噪声条件下对目标的检测性能。根据前文建立的弹载雷达信号模型,构建一种合理的检测准则以检测目标是否出现,则目标检测问题可描述为在两种假设中进行选择:H0(目标不存在)或H1(目标存在)。该假设可进一步表示为:

(28)

由于在真实场景中不能准确获取H信息,因此式(28)中H值可采用式(12)的估计值代替真实值。针对上述二元假设检验问题可根据Neyman-Pearson准则构建最优检测器[12],而能够表征该检测器性能的一个关键指标为信杂噪比(SCNR)。波形优化前后弹载雷达接收机端信杂噪比如图6所示。

图6中所示,以LMSE准则优化后的信号相比优化前LFM信号能够显著提高弹载雷达接收机信杂噪比。值得注意的是,当信号发射功率达到一定值时,噪声对信杂噪比的影响可忽略不计,雷达接收机端信噪比趋于稳定,即

LFM信号相比优化信号信杂噪比提升速率更低,但最终也会达到相同的定值。在此基础上,优化前后弹载雷达对目标检测性能如图7所示。

图6 优化波形与LFN波形SCNR

图7 优化波形与LFM波形检测性能

图7中展示了虚警概率分别为Pfa=10-2,Pfa=10-4及Pfa=10-6条件下,弹载雷达对目标检测概率随发射功率变化趋势。从图中可以看出,当虚警概率为Pfa=10-2,发射功率为250 W时,弹载雷达发射优化信号可最先达到最高检测概率,而此时发射LFM信号的检测概率仅为0.7,若要得到最高检测概率,发射功率需达到500 W甚至更高;当发射功率相同时,随着虚警概率的增大,弹载雷达发射优化信号与LFM信号间检测概率差异如表1所示:

表1 发射功率为500 W时检测概率对比

从表1中可以看出,当发射功率相同时,虚警概率由Pfa=10-2变化到Pfa=10-6时,发射信号优化后检测概率随虚警概率变化下降0.2,而发射LFM信号后检测概率变化0.71;当虚警概率相同时,发射优化信号的检测概率均高于LFM信号。综上所述,相比LFM信号,优化信号能显著提高弹载雷达对目标的检测概率且检测性能更稳定。

4 结论

导弹飞行速度快,信息获取实时性要求高,如何能够快速准确的获取目标信息直接制约着导弹制导精度。针对以上问题,文中提出了一种在杂波与色噪声条件下面向随机扩展目标的弹载雷达波形优化方法。该方法建立信号模型,基于认知理论以线性最小均方误差为准则,采用注水法在频域内优化弹载雷达发射信号能量分配,提升弹载雷达对目标频率响应的估计能力。结果表明,算法可针对目标频率响应、杂波及色噪声的相对强度合理分配发射信号的频域能量,提高目标估计精度,进一步提升弹载雷达对目标检测性能。