高斯白噪声激励下微悬臂梁的瞬态均方响应研究

张文花，李俊林，谢秀峰，董安强

(太原科技大学 应用科学学院，太原 030024)

微机电系统(MEMS)在仪器测量、航天航空、生物医学和环保等领域有巨大的应用前景[1-2]。而微悬臂梁作为MEMS的重要组成部分，对它的研究是必不可少的[3]。微悬臂梁在物流运输，仓库储存等工作过程中容易受到随机激励产生振动，尽管科研人员对微悬臂梁进行了大量而广泛的研究工作，但是对微悬臂梁在随机激励下的响应等方面的研究工作还存在不足，这使得MEMS在实际生活中的应用缺乏相关理论支持，从而使得MEMS不能被广泛的应用。因此，研究微悬臂梁在随机激励下的响应是有意义的。

丁建宁等通过对微悬臂梁进行研究，建立了梁的方程[4]。武洁等研究了微悬臂梁系统动力学特性，建立了系统连续模型，得到了振动控制方程，并分析了不同结构参数对系统动态响应的影响[5]。许锐彬通过有限元建模方法研究了微悬臂梁系统在受到简谐振动和突然冲击时的动态响应[6]。本文将在前人工作的基础上研究微悬臂梁的瞬态均方响应。自上世纪七十年代以来，科研人员对线性或非线性系统的均方响应进行了大量的研究，并取得了重大进展。Grigoriu用平稳高斯输入求得线性系统的瞬态响应[7]。谢秀峰等研究了随机激励下非线性系统的瞬态响应[8-9]。Peng 推导了非平稳随机激励下线性系统均方响应的封闭解[10]。然而，他们评估均方响应的求解方法总是在时域或频域上进行。Hu指出响应的极点留数法可以通过系统转移函数简单的代数运算得到，进而可以得到系统的响应[11]。

综上所述，本文将采用极点留数法，在复平面上求解MEMS中微悬臂梁在高斯白噪声随机激励下的瞬态均方响应的封闭解。最后，通过对瞬态均方响应的分析，讨论了阻尼比及噪声强度对系统瞬态均方响应的影响规律。

1 集总参数建模

MEMS中常用的建模方法是集总参数建模[12-13]，而集总参数建模的核心是弹簧-质量-阻尼系统。由于微悬臂梁在MEMS中的特殊地位，作为一弹性元件，在小变形情况下，其弹性系数可以用常量k来代替，振动时的阻尼来自材料内阻尼c.故微悬臂梁振动系统可以用质量弹簧阻尼系统来模拟。如图1所示。

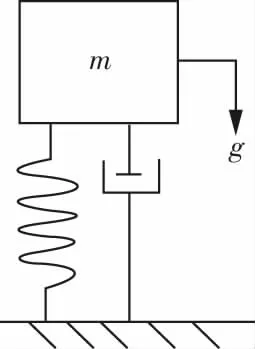
图1 弹簧质量阻尼系统模型Fig.1 Spring mass damping system model

当质量受到高斯白噪声随机激励g时，系统的运动方程可表示为：

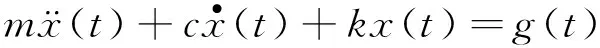
(1)

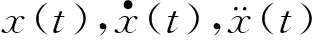
2 系统的响应

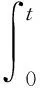
(2)

式中，h(t)为系统的单位脉冲响应函数：

(3)

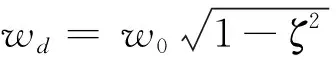
故方程(1)的拉普拉斯变换为：

(4)

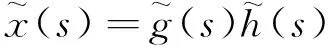
(5)

(6)

它的极点留数公式为：

(7)

μ=-ζω0+iωd

(8)

(9)

对方程(7)进行拉普拉斯逆变换，得：

(10)

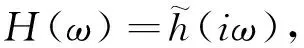
(11)

3 自相关函数和功率谱密度函数

考虑了白噪声随机激励g(t)是零均值高斯平稳随机过程，Sg(ω)和Rg(ω)分别是功率谱密度函数和自相关函数，有如下关系：

(12)

(13)

零均值的随机响应激励也是零均值，则X(t1)X(t2)的期望为：

E[X(t1)X(t2)]=

(14)

当t1=t2=t时，可以得到在t时的均方位移

E[X2(t)]=

(15)

4 平稳响应的协方差

把方程(13)代入方程(15)中，得：

(16)

由于时间变量τ1和τ2可以分离，则

(17)

令：

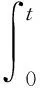
(18)

(19)

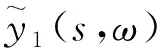
(20)

式中，

(21)

(22)

(23)

由上可知，C1(ω)=-(A1(ω)+B1(ω))，对方程(20)进行拉普拉斯逆变换，得：

(24)

令:

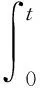
(25)

对方程(25)进行拉普拉斯变换得，

本文笔者将微课应用到成人继续教育中，将信息化教学手段融入了传统教学中，从而形成了线上线下的混合式教学模式。这种混合式教学模式是一种优秀的教学模式，它综合了MOOC的优势，弥补了MOOC缺乏管理机制的缺陷，利用现有大量的MOOC资源，降低了微课制作的工作量，突现了“互联网+”时代的优势。

(26)

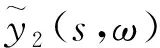
(27)

式中，

(28)

(29)

(30)

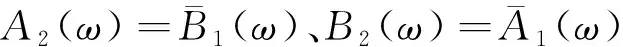
(31)

令g(t，ω)=y1(t1，ω)y2(t2，ω)，则 ：

(32)

C1(ω)C2(ω)

(33)

5 瞬态均方响应

将方程(33)代入方程(32)，可以得到在t时的均方位移为：

(34)

其中：

(35)

(36)

(37)

(38)

(39)

(40)

(41)

(42)

(43)

由上可知，E9是独立于时间t的平稳项，将方程(23)和方程(30)代入方程(43)得，

(44)

也可以写成平稳响应公式，

(45)

式中，H(ω)为系统的复频响函数。

记方程(35)-(38)这四项的和为N(t)，则N(t)为非平稳响应项；记方程(39)-(42)这四项的和为C(t)，则C(t)为交叉响应项。所以方程(34)可以写：

E[X2(t)]=N(t)+C(t)+E9

(46)

此外，方程En(t) (n=1，2，…，9)有如下关系

(2)E3(t)=E4(t)，E5(t)=E7(t)，E6(t)=E8(t)

通过使用上面的关系可以得到，

N(t)=2{Re[E1(t)]+E3(t)}

(47)

C(t)=4Re[E5(t)]

(48)

因此，计算E[X2(t)]，只需要计算E1(t)，E3(t)，E5(t)和平稳项E9.如果SF(ω)是数值给定的，那么积分项E1(t)，E3(t)，E5(t)和E9必须用数值计算。对于解析函数SF(ω)，只要它能被表示成极点留数形式，就可以推导出E[X2(t)]的精确闭式解。

[-ζ2ω2+2(ζω0sinωdt)2+ζω0ωdsin2ωdt]

(49)

(50)

(51)

(52)

由上可知，微悬臂梁的瞬态均方响应为：

(53)

方程(53)中所示的E[X2(t)]与之前通过其他方法(Caughey和Stumpf 1961)获得的是相同的。

对于高斯白噪声激励情况，C(t)=-2N(t)，即Re[E5(t)]=-Re[E1(t)]-E3(t).

6 瞬态均方响应分析

本文所研究的微悬臂梁系统所选取的数值为：质量m=10；无阻尼固有频率ω0=5；阻尼比ζ=2%；噪声强度S0=0.01.

如方程(46)所示，瞬态均方响应是非平稳项N(t)、交叉项C(t)和平稳项E9的和。根据瞬态均方响应、非平稳、交叉项和平稳项的表达式画出图像如图2所示。通过图像可以发现，当t变大时，N(t)和C(t)趋于零，而E[X2(t)]趋于一个固定值，完全由E9决定。

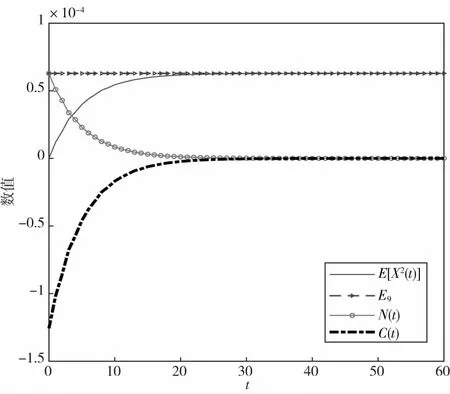
图2 瞬态均方响应Fig.2 Transient mean square response

可以得到静止初始条件时刻的一些特征：N(0)=E9，C(0)=-2E9，E[X2(0)]=0.

为了研究系统的特性，下面分别代入阻尼比不同的值和噪声强度不同的值，并得出相应的结果。其结果如图3-图4所示。其中，图3为噪声强度S0=0.01时阻尼比不同的情况，从图3中可以看出，当t变大时，瞬态均方响应先增大后趋于平稳。当阻尼比较大时，瞬态均方响应较小，且瞬态均方响应趋于平稳的时间短。当阻尼比趋近于零时，瞬态均方响应随着时间的增加而趋于无界。图4为阻尼比为ζ=2%时噪声强度不同的情况。从图4中可以看出，当t变大时，瞬态均方响应先增大后趋于平稳。当噪声强度大时，瞬态均方响也大，且瞬态均方响应趋于平稳所用的时间比较长。当噪声强度趋近于零时，瞬态均方响应也趋于零。

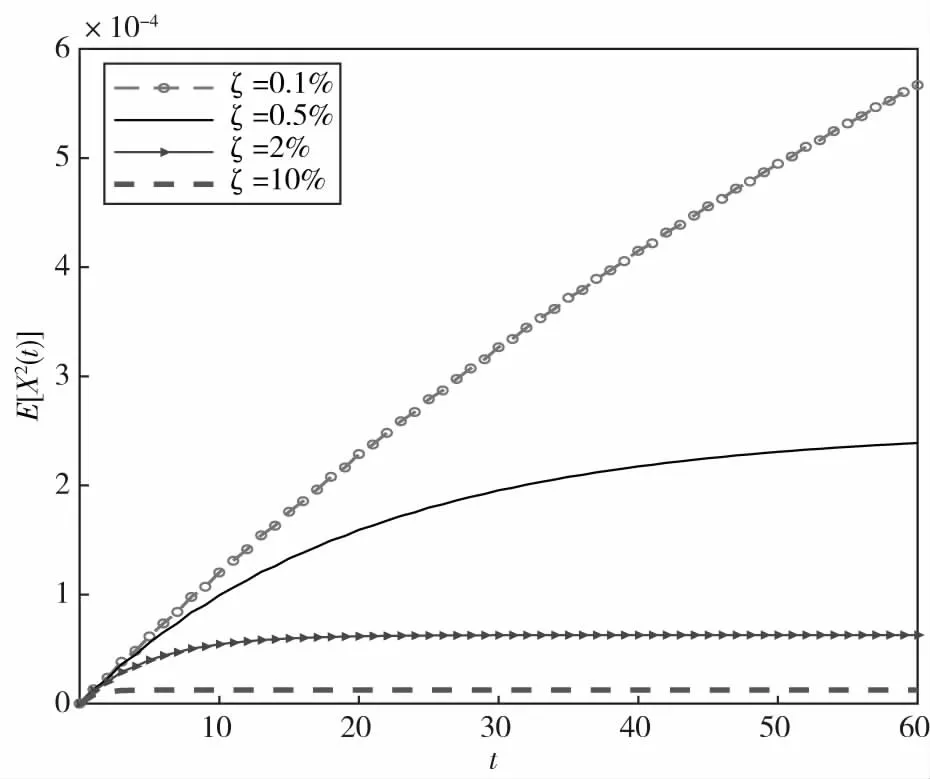
图3 瞬态均方响应在不同阻尼比下的变化规律Fig.3 The variation law of transient mean square response under different damping ratio

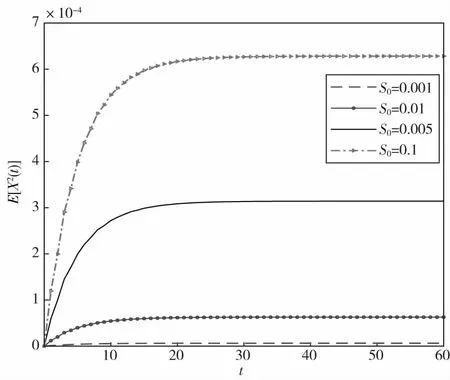
图4 瞬态均方响应在不同噪声强度下的变化规律Fig.4 Variation law of transient mean square response under different noise intensity

7 结论

本文的主要是利用了极点留数法，推导出了微悬臂梁在以高斯白噪声功率谱密度函数为特征的随机激励下的瞬态均方响应的封闭解。该方法的一个显著优点是在求解过程有效地避免了在时域计算积分的繁琐。最后通过对瞬态均方响应的分析，给出了阻尼比和噪声强度对系统瞬态均方响应的影响规律。研究表明，当阻尼比较大时，瞬态均方响应较小，且瞬态均方响应趋于平稳的时间短。当噪声强度较大时，瞬态均方响也较大，且瞬态均方响应趋于平稳所用的时间比较长。