燃气射流载荷和风载荷对适配器分离影响研究*
2018-12-21宋双婧于骐瑞王新星
殷 鑫,宋双婧,于骐瑞,王新星,赵 鑫,李 军
(1 南京理工大学机械工程学院,南京 210094;2 湖北江山重工有限责任公司,湖北襄阳 441000;3 中国兵器工业导航与控制技术研究所,北京 100089)
0 引言
对于采用倾斜发射的火箭炮,因其火箭弹较重,为了减小离轨瞬间因重力造成的弹头下沉而引起的起始扰动,常常采用同时离轨技术予以解决。同时离轨是指火箭弹的前后定心部同时与发射装置脱离约束,这样火箭弹重力对质心的重力矩就不存在了,火箭弹缺少俯仰的力矩输入,就可以避免由于火箭弹初速较低而带来的超过规定的俯仰角或者角速度,文中通过在低轨与火箭弹之间采用适配器的方式实现火箭弹的同时滑离。适配器技术[1]在火箭弹中应用较少,但在导弹中应用广泛。国外的导弹武器如“北极星”导弹、“三叉戟”导弹等均已经成功的采用了该技术,中国多种类型导弹发射也采用了适配器技术。
RUDD等利用EPDM作为适配器的本体材料,建立了适合MX导弹系统所需的空心适配器[2]。秦丽等提出了用火箭弹弹性适配器实现被动控制发射[3]的新方法。董贵使用有限元软件SAP5对某型导弹发射系统适配器的强度进行了计算[4]。施俊凯设计了计算适配器受风载作用时在空中运动轨迹的软件,并做了可视化开发[5]。高强等研究了分离力作用在不同位置及风速不同时对适配器分离过程的影响[6]。黄聪基于流体力学计算软件对风载荷做了详细的研究,并将结果加载到适配器上,研究了适配器空中运动轨迹[7]。
前人的研究都是建立在冷发射导弹基础上的,即只考虑风载荷的影响。但这在火箭弹中是不适用的,因为适配器在与火箭弹分离后,还会受到火箭弹燃气射流冲击载荷作用,文中在研究适配器分离运动时,提出了一种简化的燃气射流冲击力的加载方法,并运用ADAMS软件研究适配器的分离运动,分析其落点位置是否安全及在分离过程中是否会与火箭弹发生二次碰撞。
1 适配器结构
适配器结构包括适配器主体、解锁杆、弹簧导杆、分离弹簧和弹簧垫片。适配器位置示意图及结构图如图1所示。当火箭弹发射时,适配器在弹簧导杆的带动下随火箭弹一起运动,在适配器运动到发射箱口部时,适配器底面与低轨分离,适配器底部完全放开,在弹簧预紧力的作用下,适配器会与火箭弹快速分离,防止其对火箭弹的飞行造成影响。

图1 适配器位置示意图及结构图
2 ADAMS建模与分析
2.1 刚体建模及坐标系定义
将发射箱实体模型进行简化,得到如图2所示刚体分析模型(隐去了蒙皮和一部分侧梁)。文中所涉及坐标系如下:
1)全局坐标系OXYZ,坐标原点O位于发射箱下轨后端,与下轨后端中点重合,X轴与火箭弹0°射角时方向相同,Z轴垂直向上,Y轴满足右手螺旋法则。
2)火箭弹坐标系O1X1Y1Z1,用于加载火箭弹推力曲线,坐标原点O1与火箭弹质心重合,X1轴沿火箭弹弹轴方向,指向箱口方向为正,Z1轴垂直于低轨平面,指向上方,Y1轴满足右手螺旋法则。
3)适配器坐标系O2X2Y2Z2,坐标原点O2与适配器质心重合,X2、Y2、Z2坐标轴方向分别与X1、Y1、Z1坐标轴方向一致。

图2 发射箱刚体模型
2.2 接触关系及边界条件定义

文中发射箱刚体模型中存在的接触关系有:适配器主体与火箭弹,适配器主体与下轨,火箭弹与下轨,定向钮与闭锁挡弹装置,适配器主体与弹簧垫片,弹簧垫片与火箭弹。
文中模型为刚体模型,不考虑发射过程中箱体变形带来的影响,所以在边界条件的设定上是将发射箱箱体与大地固连。
2.3 风载荷加载
风载荷以集中力的方式加载在适配器的质心上,计算公式为:
(1)
式中:C为载荷系数;ρ为空气密度;S为迎风面面积,v为空气流动速度。
从式(1)中可以知道,风载荷的主要影响因素是物体的迎风面面积及物体与空气的相对速度。
文中适配器分离弹簧作用位置在距离质心前端70 mm处,所以在适配器与火箭弹分离时,适配器会在弹簧分离力作用下转动。这样适配器的迎风面就会时刻变化,同时在实际情况中,空气中风速大小及方向也是实时变化的。两种无规则变化会使力F的变化也无规则。为了便于计算,对风载荷做了以下假设:
1)风速大小、方向恒定,始终沿OX轴方向。
2)适配器在空中翻转过程中,迎风面面积实时变化,但其存在最大值和最小值。如图3所示,当适配器处在横向位置时迎风面面积最小,当适配器处在垂直位置时迎风面面积最大。文中假设适配器的迎风面面积恒定,在其它条件不变的情况下,分别取最大迎风面和最小迎风面两种面积进行研究。
3)假设风力载荷始终垂直作用在适配器迎风面上,即假设适配器在空中姿态不变,这时载荷系数C取最大值1。

图3 迎风面
文中假设风载荷方向始终沿X轴方向,即适配器运动方向,当沿X轴正向加载时为顺风,负向加载时为逆风。1990年到2010年某地区风速统计如表1所示。

表1 风速统计
从表1中可以看出,4 m/s到8 m/s的风速出现的概率最高,所以一种风速选择6 m/s。同时根据发射要求可知,火箭炮发射时风速不应超过12 m/s,另一种风速选取极端情况12 m/s。同时还选取0 m/s风速,即适配器在空中运动只受空气阻力,这种情况用来研究燃气射流简化加载方法对适配器落点规律影响。
2.4 燃气射流载荷加载
火箭炮燃气射流属于自由射流,其在实际情况下射流主段的轴心速度和径向速度均按照指数规律衰减,但其变化规律比较复杂,理想的方法是通过实验获取燃气射流流场风速分布数据,但这几乎是不可能完成的事,文中在研究小组大量实验测量数据的基础上,提出了一种简化处理燃气射流风速场的方法,对燃气射流作用区域内燃气速度变化规律做出如下简化处理:
1)燃气在沿火箭弹轴线方向先将速度以一较大斜率衰减到某一值,再以一相对平缓的斜率衰减到0。
2)燃气在弹径方向上,从圆心到射流边界线性衰减到0。
3)燃气射流流场内任意一点的燃气速度方向为弹尾圆心与该点连线的方向。
当适配器运动到燃气射流作用区域内某一点时,燃气射流对适配器作用如图4所示。
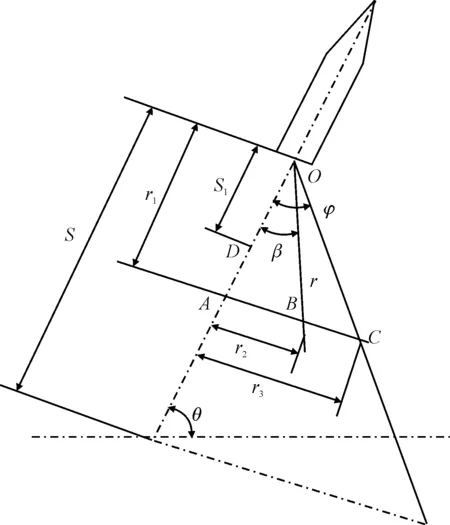
图4 燃气射流作用示意图
图4中,O点为火箭弹尾部中心点;B点为适配器在燃气射流作用区域内的位置;A点为火箭弹轴线上一点,且直线OA垂直于直线AB;C点为直线AB与燃气射流外边界的焦点;D点为燃气射流沿轴线衰减的拐点;r表示OB两点间距离;r1表示OA两点间距离;r2表示AB两点间距离;r3表示AC两点间距离;s表示燃气射流从喷口到衰减为0的距离;s1为OD两点间的距离;θ表示射角;β表示直线OB与火箭弹轴线的夹角,φ表示燃气射流外边界与火箭弹轴线的夹角。
因为燃气射流流速沿火箭弹轴线经过两段线性衰减最终变为0,所以火箭弹轴线上A点的燃气射流流速可表示为:
(2)
式中:vO为火箭发动机喷口处燃气射流流速;vD为燃气射流沿轴线衰减拐点的流速。
同时,在弹径方向上,燃气射流流速从圆心到射流边界线性衰减到0。所以在求得vA后,可以得到燃气射流作用区域内B点的燃气射流流速:
(3)
再将式(3)中求得的速度代入到式(1)中就可得到适配器在该位置时简化的燃气射流冲击载荷。
文中分别选择距弹尾3 m、6 m、9 m处为燃气射流速度变化的拐点,即s1分别取3 m、6 m、9 m,同时拐点处速度vD分别取800 m/s和600 m/s进行研究。
3 仿真结果及分析
3.1 适配器落点范围
根据适配器迎风面面积、适配器拐点位置及拐点位置处速度、风速的大小和方向的不同,分为11种情况研究适配器落点范围。
情况1和情况2为研究适配器迎风面面积对落点的影响。情况1取最小迎风面面积0.035 m2,情况2取最大迎风面面积0.088 m2,风速取0 m/s,燃气射流沿轴线衰减拐点为距火箭弹弹尾9 m处,在拐点处燃气射流速度为800 m/s。此时适配器沿OX方向位移曲线如图5所示。具体数值如表2所示。
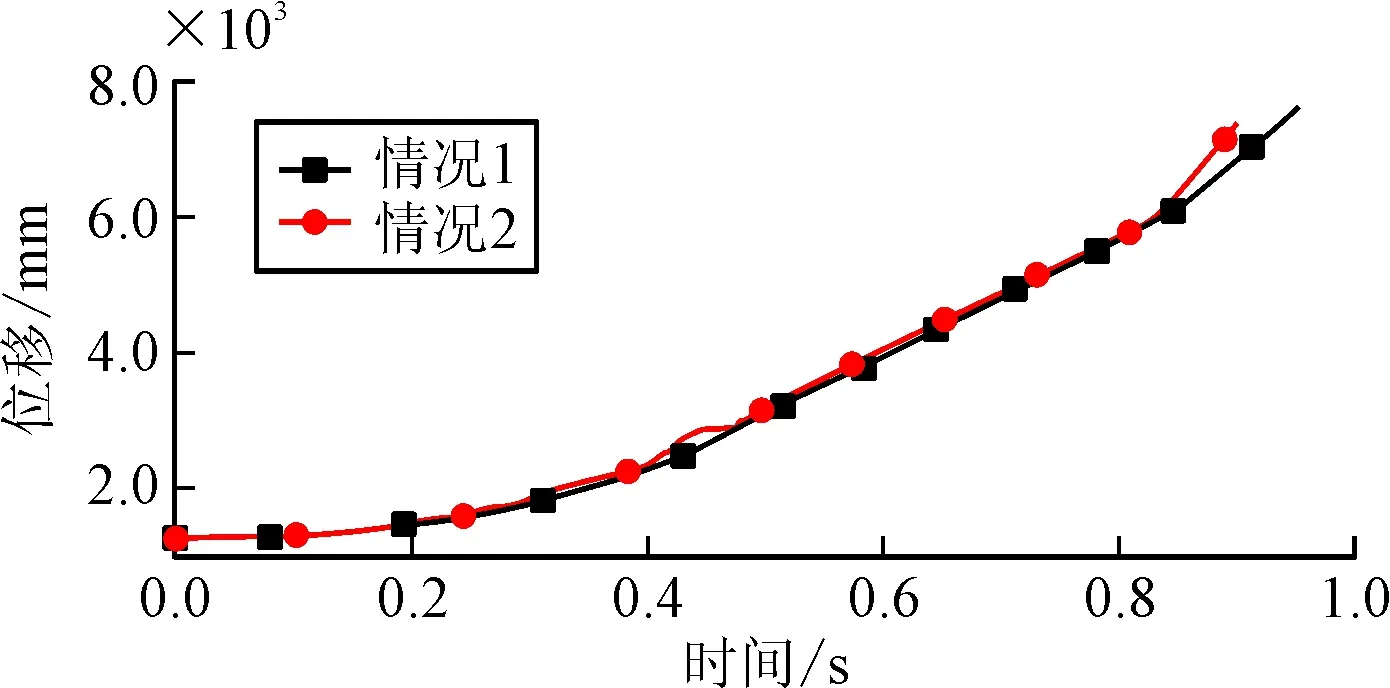
图5 适配器OX方向位移曲线

情况1情况2落地时间/s0.9510.915落地距离/m7.637.55
情况3到情况7为研究燃气射流载荷沿火箭弹轴线不同衰减规律对适配器落点的影响。即只改变燃气射流轴向衰减拐点位置及拐点上燃气射流速度大小,其他条件与情况1相同。具体情况见表3。

表3 情况列表
此时适配器沿OX方向位移曲线如图6所示。具体数值如表4所示。

图6 适配器OX方向位移曲线

情况3情况4情况5情况6情况7落地时间/s0.9721.0000.9650.9971.046落地距离/m7.777.897.767.918.01
情况8到11为不同风速、风向对适配器落点的影响,其他条件与情况1相同,情况说明见表5。

表5 情况列表
此时适配器沿OX方向位移曲线如图7所示。具体数值如表6所示。

图7 适配器OX方向位移曲线

情况8情况9情况10情况11落地时间/s0.9540.9550.9450.936落地距离/m7.677.697.387.12
可以得到以下结论:
1)对比情况1和情况2,虽然两种情况下适配器落地时间不同,但落地时X轴方向位移差别很小,可忽略不计。后续的研究中只取最小迎风面面积作为研究对象。
2)对比情况3到情况7,对于同一拐点位置,拐点处燃气速度越高适配器落地所需时间越短,适配器沿X方向位移越小;对于同一拐点燃气速度来说,拐点位置越远,适配器落地所需时间越短,适配器沿X方向位移越小。
3)对比情况8到情况11,适配器在顺风情况下沿X方向位移随风速增加而增大,但变化不大,所以顺风风速对适配器落点影响可忽略不计。适配器在逆风情况下位移随风速增加而有明显减小,从风速0到风速12 m/s减小了0.51 m。
4)综合考虑情况1到情况11,可知情况11中适配器落点最近为7.12 m。
情况7中适配器落点最远为8.01 m。已知发射车长12 m,因此在68°高低射角下,如果发射过程中方向角为0°,在发射过程中适配器会落到车上,存在安全隐患。
3.2 适配器与火箭弹二次碰撞问题
适配器与火箭弹发生二次碰撞只可能出现在适配器还没越过火箭弹弹尾的阶段,此阶段适配器只受风载荷的影响。已知在顺风情况下,风载荷对适配器的作用方向是向前的,这会加速适配器与火箭弹的分离。但逆风情况则正好相反,风载荷会将适配器往靠近火箭弹的方向作用。文中选取情况11来研究适配器与火箭弹二次碰撞问题,此时适配器与火箭弹相对位置关系如图8所示。

图8 适配器与火箭弹相对位置曲线
从图8中可以看出,初始时刻,适配器距火箭弹弹尾4.16 m,在t=0.766 s时,轴向距离变为0,即火箭弹弹尾追上了适配器。在这个过程中,适配器与火箭弹分离后其径向距离是逐渐增大的,在t=0.766 s时已经达到1.5 m,所以适配器不会与火箭弹发生二次碰撞。
4 结论
文中利用ADAMS软件对某型火箭弹与适配器分离情况进行了计算和分析,提出了一种简化的燃气射流载荷加载方法,分析了不同风速、风向及燃气燃速衰减规律时的适配器落点范围及与火箭弹的二次碰撞问题,可以为分离方案的确定和适配器结构方案确定提供参考。由于文中对燃气载荷及风载荷的加载做了一定的简化,所以仿真结果与实际情况有一定的偏差。
