基于组合预测模型的惠安县快递业务量需求预测分析

王凤英 （福建船政交通职业学院，福建 福州 350007）

0 引言

近几年，电子商务迅速发展，对快递物流的需求进一步提升。但部分地区物流设施和技术落后，物流末端配送发展滞后，物流服务体验差，物流企业各自为营，企业进行农村物流配送成本高，因此为了提升快递物流的服务水平，必须对未来的快递业务量有个合理的预测，进而配备相匹配的设施及技术。需求的定量预测模型主要有回归分析预测法、时间序列预测法、神经网络预测法、灰色预测法等多种方法，但单一的预测模型的假设条件及使用范围总存在着一定的局限性，因此本文最后采用组合预测模型克服单一模型的局限性，提高模型预测的精度和稳定性。

1 惠安县快递业务的发展现状分析

惠安县，是闽南著名侨乡和台湾汉族同胞主要祖籍地之一。素有“海滨邹鲁”、“雕艺之乡”、“建筑之乡”、“渔业强县”、“食品工业强县”之美誉。2017年全县实现生产总值688.76亿元、增长8%，完成一般公共预算收入35.13亿元、增长3.1%，全体居民人均可支配收入2.99万元、增长7.5%，县域经济居全国中小城市综合实力“百强县”第35位。

在电子商务迅速发展的大背景下，随着GDP的逐年稳步提高，人民的消费水平大幅提高，惠安县的快递服务需求总量也随之持续增长，具体见图1。

2 预测模型的选择与构建

快递业是随着电子商务发展起来的新兴行业，近10年发展迅速，并与区域经济发展密切相关。因此快递业务量受到区域经济发展多种因素的影响，如区域经济的经济水平和规模、居民人均消费水平、社会固定资产投资总额，常住人口、社会消费品零售额的影响。同时也会受到国家相关政策、信息处理技术及交通因素等非经济因素的影响。因此在构建预测模型时选取了

4 种预测模型进行预测。

2.1 多元回归关系模型的构建。由于快递业务量的影响因素是多方面的，因此在预测时首先考虑了多元回归关系模型。多元回归关系模型中的解释变量有多个，一般形式为：

其中，y是被解释变量（因变量、相依变量、内生变量），x是解释变量（自变量、独立变量、外生变量），ε是随机误差项，βi,i=1,2,…,k是回归参数。

利用初始变量值进行回归并检验，若模型未通过检验，则重新建立模型，若模型通过检验，且满足模型的假设，则可利用此模型进行实际预测。

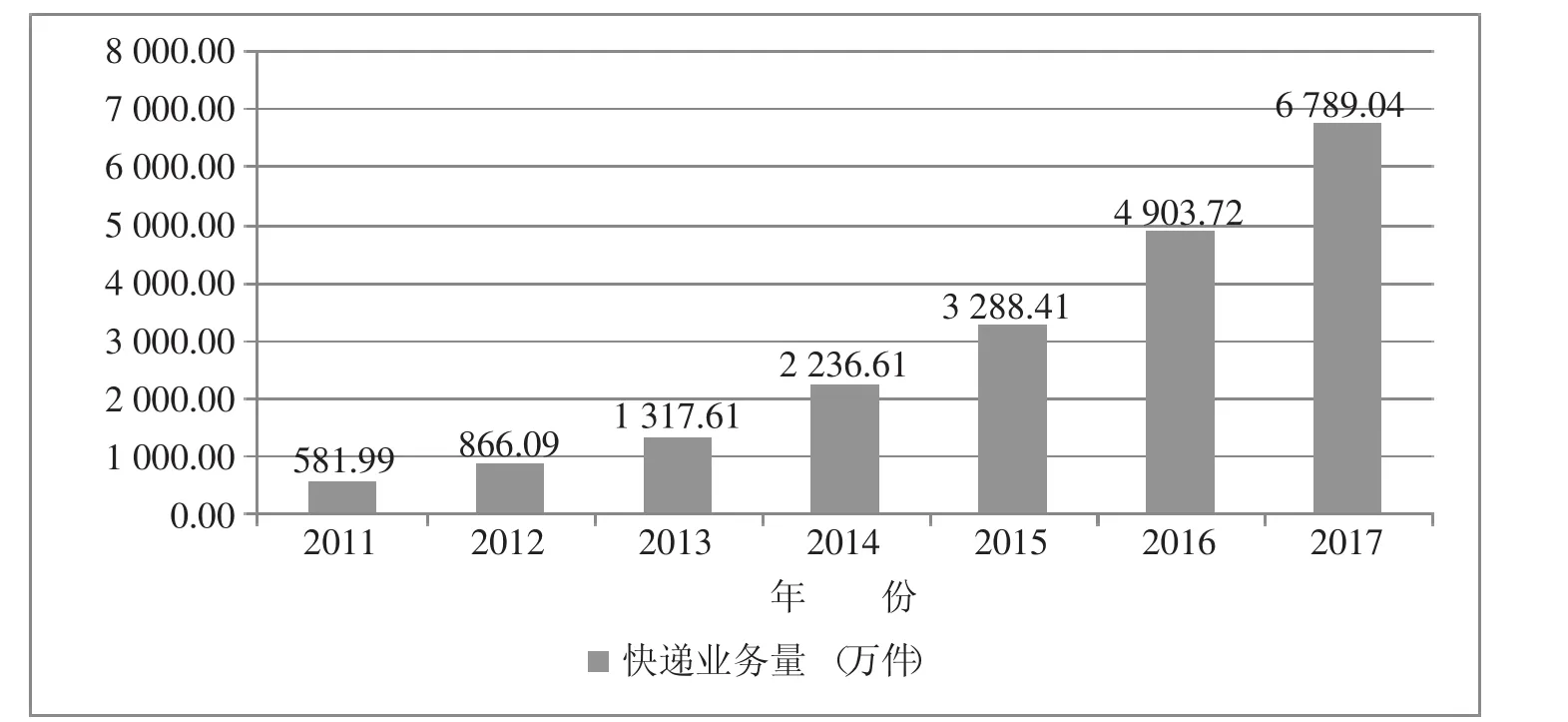
图1 惠安县历年快递业务量增长趋势图

2.2 基于时间序列的多项式回归模型构建。快递业务量是一个时间序列，通过上述现状分析图1可以看出近几年惠安县快递业务量没有跳跃式增长，属于渐进变化，同时快递业是一个迅速发展的行业，因此可选用二次多项式趋势回归预测模型构建。多项式趋势回归预测模型建立如下：

本文采用二次多项式趋势回归对快递业务量进行预测。

2.3 GM（ 1,1）灰色预测模型构建。灰色预测模型是应用模糊数学原理对既含有已知信息又含有不确定信息的系统进行预测的模型，是对随机的原始时间序列数据进行累加生成处理，然后建立微分方程来模拟该生成序列，恢复原时间序列的预测值。GM（1,1）模型是最常用的一种灰色预测模型。具体预测模型如下：

建立微分方程和构造矩阵。

构造矩阵B：

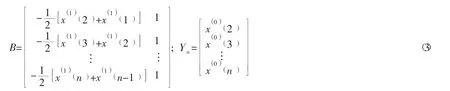
矩阵计算：

求出预测模型：

将参数代入时间函数得一次累加生成序列的预测模型：

最后通过一系列检验来检验模型的精度和可信度。

2.4 Shapley组合预测模型。上述3种预测方法各有优缺点，因此为了提升预测精度，对上述3种预测方法赋予不同的权重进行最后预测结果的运算。目前最常用的就是Shapley组合预测模型。其计算公式为：

Shapley值误差分配公式为：

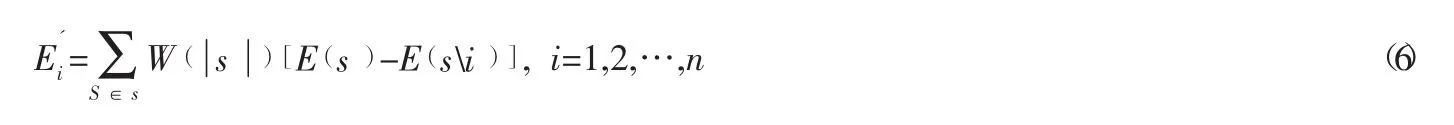
Shapley值法给出了一个n人合作对策问题的分配向量，u（s）-u（ si）表示组合S的边际贡献值，考虑了组合成员加入后和加入前对组合产生不同的影响。）可看作一个权重，表示组合成员i在组合中所需要承担的边际贡献，也是组合预测的加权因子。Shapley值综合了组织中各成员的影响，因此可认为其分配向量是公平合理的。

由上可得权重计算公式：

3 惠安县快递业务量预测分析

3.1 多元回归关系模型预测。在对快递业务量的影响因素分析基础上本文选用了GDP、常住人口、居民人均消费水平、社会消费品零售额、固定资产投资总额作为快递业务量的解释变量。具体数据见表1。选用spss19.0对表1的数据进行多元回归分析。首先进行了相关性分析，快递业务量与这几个解释变量的相关性均在0.9以上，故显著相关，然后选用向后回归进行分析，具体结果见表2。

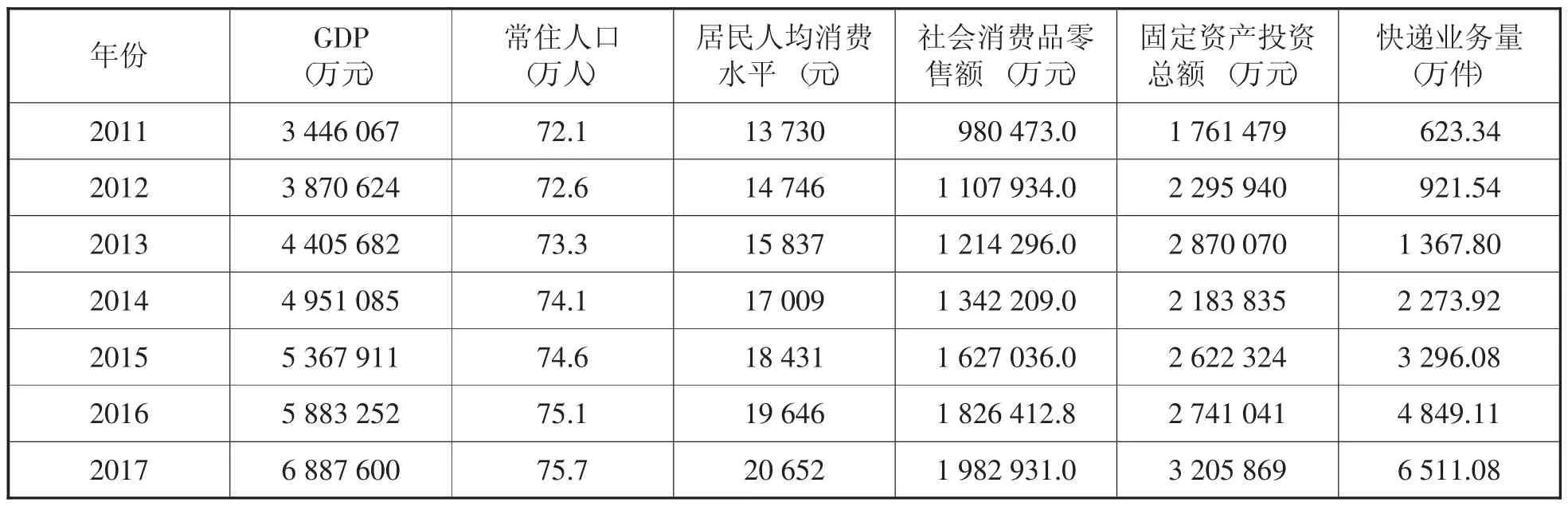
表1 2011～2017年惠安县快递业务量相关指标数据

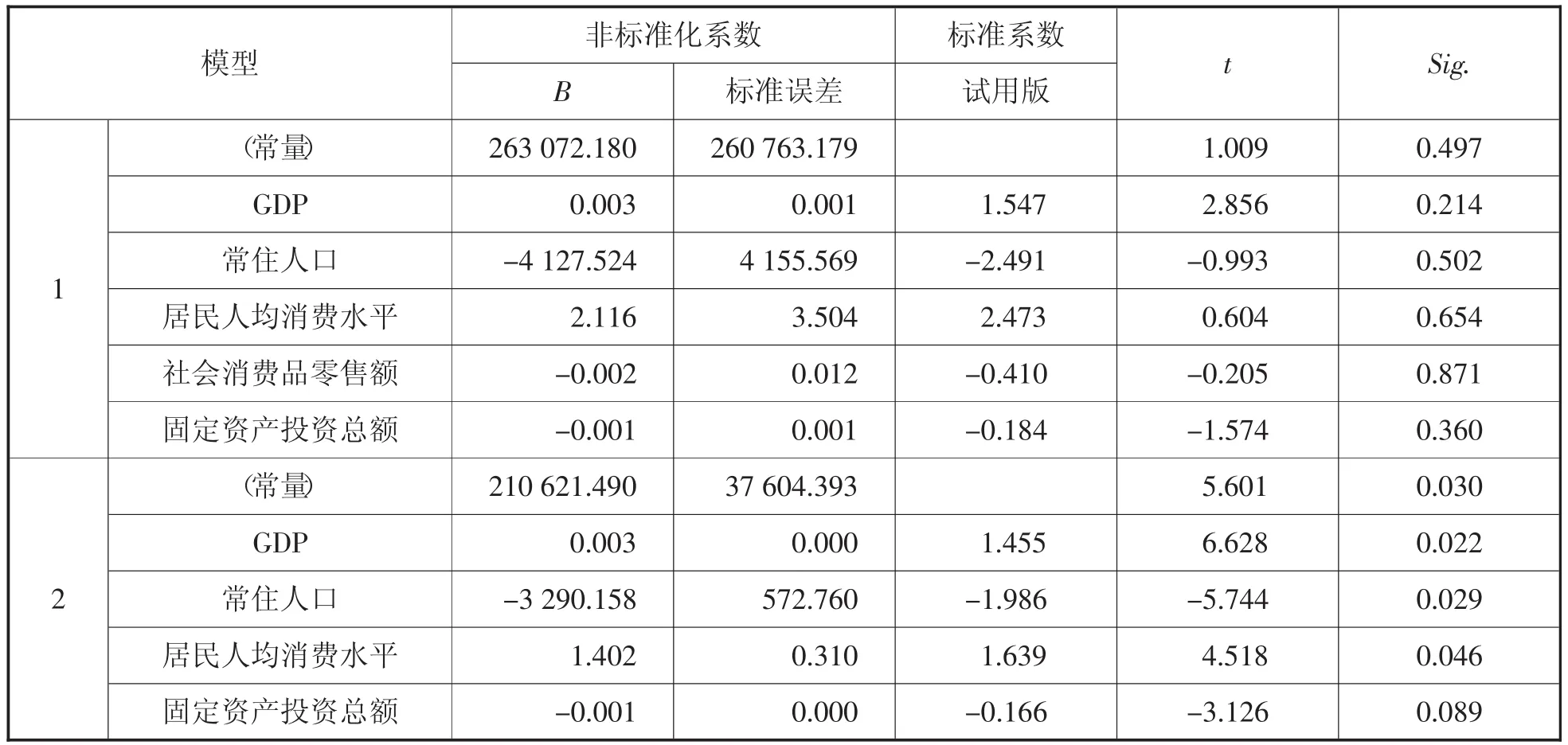
表2 系数a

a.因变量：快递业务量

根据上述分析结果可以看出社会消费品零售额被移除了，但调整后的R方仍可以达到0.994。根据系数表，多元回归方程为：

快递业务量=210 621.490+0.003*GDP-3 290.158*常住人口+1.402*居民人均消费水平-0.001*固定资产投资总额

代入上述回归方程计算出2011～2017年的快递业务量的预测值，见表3。

根据表3可以计算出多元线性回归模型的平均绝对误差比为5.58%。

利用二项式曲线回归模型对2019～2022年影响快递业务量的各指标进行预测，然后代入上述多元线性回归模型计算出快递业务量，结果见表4。

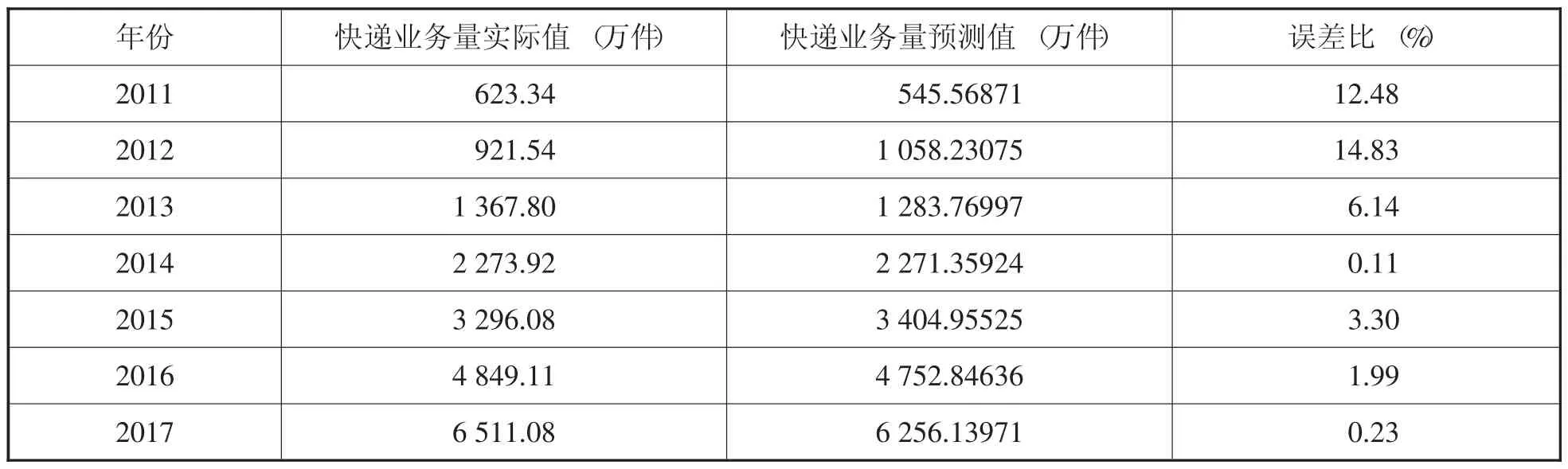
表3 多元线性回归模型预测值

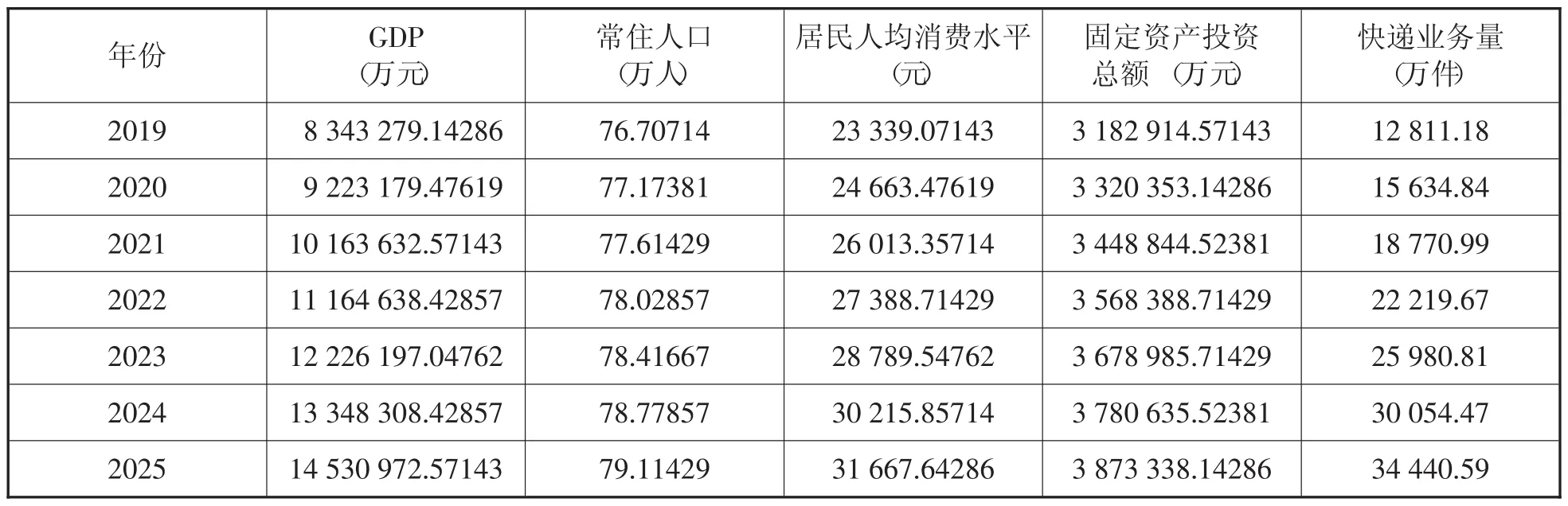
表4 2019～2025年惠安市快递业务量相关指标数据

3.2 二次多项式趋势回归模型。本文选用spss19.0软件对软件快递业务量的影响因素进行二次多项式回归。运行结果见表5。

表5 模型汇总和参数估计值

由表5可知R方为1.00，说明拟合程度很高，能较好地反应快递业务量的变化，模型拟合值见表6，平均绝对误差比为2.31%，效果很好。

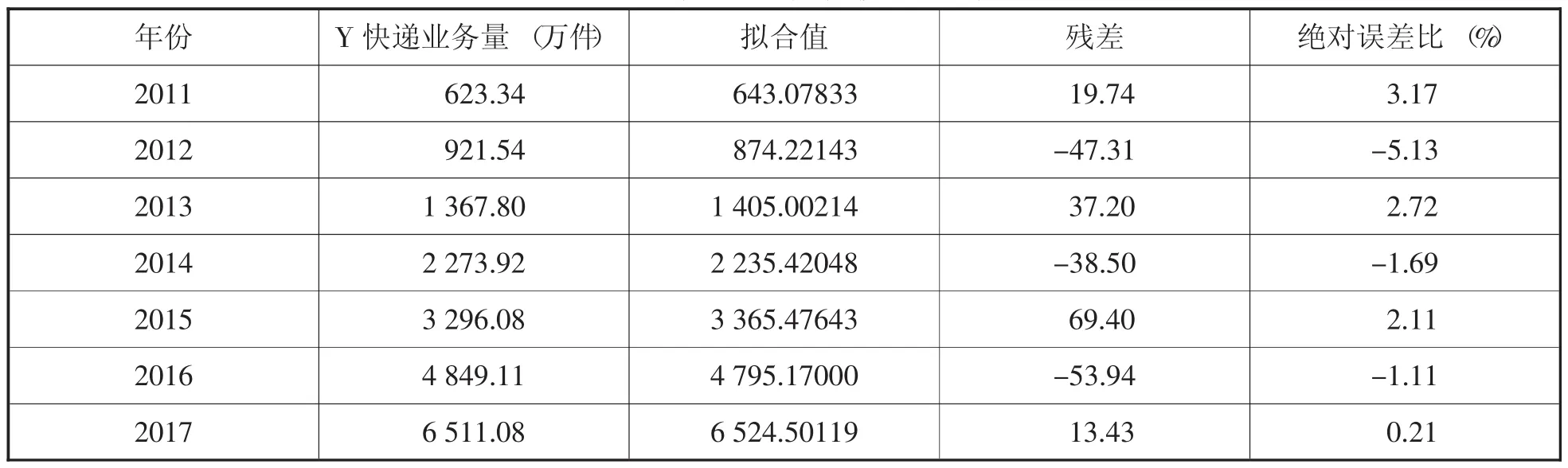
表6 二次多项式回归模型拟合值

利用二项式趋势回归法对2019～2025年进行预测得到结果如表7。

3.3 灰色预测方法。采用灰色预测分析软件，对原始数据进行模型GM（ 1,1 ）分析，残差=145 262.37，平均相对误差=6.26%，系数=757.93。模型误差分析见表8。

利用灰色预测方法对2019～2025年进行预测结果见表9。

3.4 Shapley组合预测模型。由Shapley组合预测模型中计算各预测方法权重ωi的公式可以得到ω1=0.26，ω2=0.55，ω3=0.19。说明趋势回归法在组合模型中权重最大，多元线性回归模型最小。

表7 2019～2025年二项式趋势回归预测值

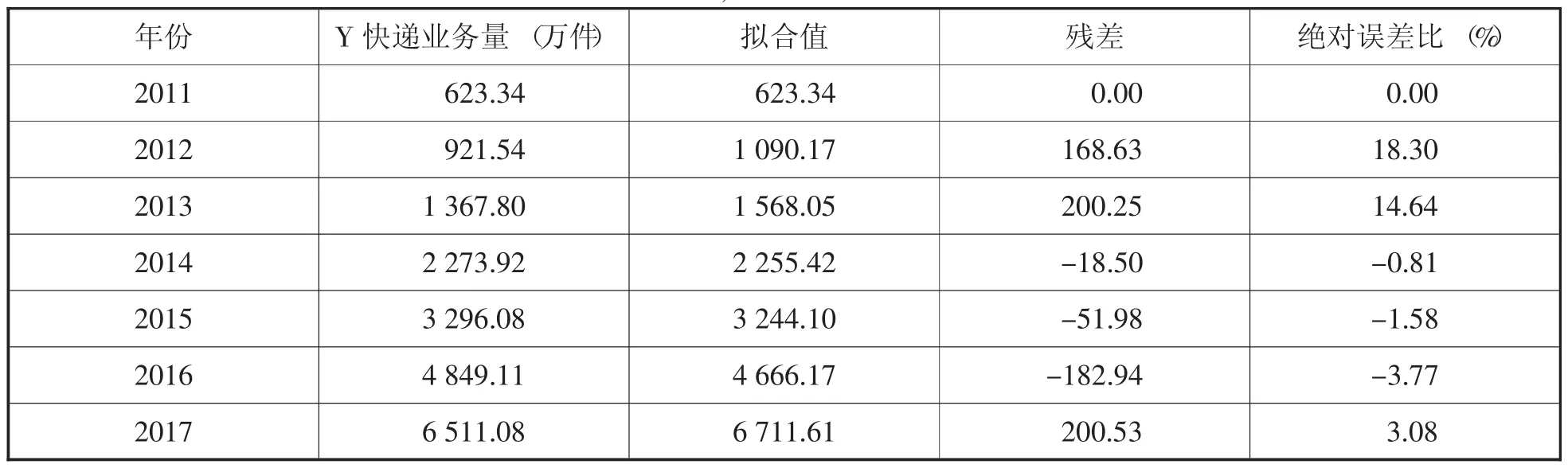
表8 GM（ 1,1）模型预测误差分析

表9 灰色预测方法的预测值

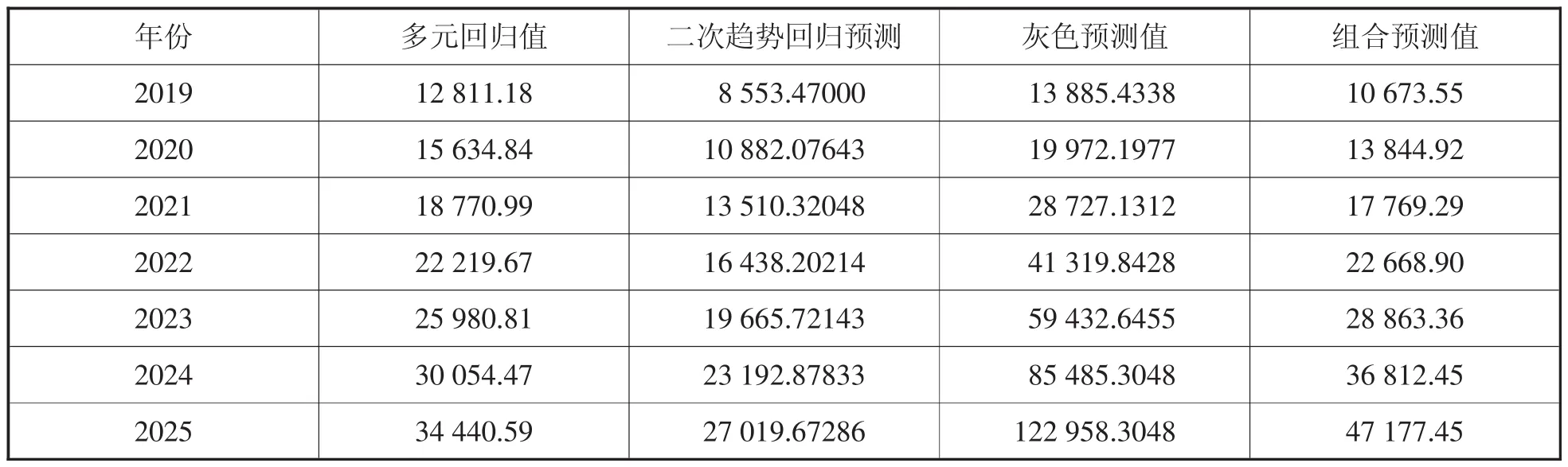
表10 2019～2022年组合预测结果

利用公式（8）可以得到惠安县快递需求量组合预测结果见表10。

4 结束语

在快递业务量的需求预测中，单个预测方法存在一定的局限性，因为本文在选择了多元线性回归、多项式趋势回归、灰色预测方法的基础上，对惠安县快递业务量利用组合预测方法进行预测，预测精度得以提升，从而对惠安县的物流网络规划提供了一定的指导意义，提升物流网络设施设备的合理布置，更好地提升服务效率，与电子商务及经济发展相匹配。