基于层次分析法的加油站选址研究

王彬彬，张 宁 WANG Binbin,ZHANG Ning

（上海理工大学 管理学院，上海 200093）

0 引言

城市加油站作为大城市建立石油石化产品的终端销售系统，是汽车加油的主要场所。它们在社会经济活动中起着重要的作用。加油站的科学定位直接影响到整个成品油销售网络的运行效率，同时对城市环境和安全也有一定的影响[1]。因此，有必要对加油站的选址方案进行决策分析，合理确定加油站的选址、规模和效益，构建经济、合理、安全、高效的终端销售网络。

常用的选址方法有重心法、鲍姆儿～沃尔夫（Baumol—Wolfe）法、德尔菲法、层次分析法、整数规划法等[2]。对加油站选址的研究方法有阿德兰启发式算法[3]，助GIS空间分析方法[4]等。本文应用层次分析法（AHP）对加油站选址中的经济因素、安全环境因素、加油量进行了综合考虑。通过量化由备选方案提供的数据，构造对比矩阵。以MATLAB数学软件为工具，通过层次单排序、层次总排序和一致性检验得到最优定位方案。

1 层次分析法

层次分析法（AHP）是一种定性与定量相结合的多目标决策分析方法。该方法主要是通过将复杂问题分解为若干层次和若干因素，建立判断矩阵，计算判断矩阵和相应的特征向量的最大特征值，以及不同的权重，为方案的选择提供依据[5]。本文采用层次分析法（AHP）对加油站选址问题进行了研究，在使用该方法时，可以利用层次分析法确定各因素的权重。对于加油站的选址，可以采用层次分析法来更好地分析各种因素对总体目标的影响。在此过程中，通过计算机计算，进行一致性检验，以确定加油站站点选择的最佳决策。

AHP的最大优点是它可以处理定性和定量问题。它可以将决策者的主观判断和政策经验引入模型并对其进行量化[5]。层次分析法本质上是一种科学思维方式。其主要特点是：（1）针对具有层次结构的整个问题的综合评价，将问题逐层分解，转化为多个单准则评价问题。（2）为了解决定性因素的处理和可比性问题，Saaty提出“重要性”比较作为统一的处理格式，并且比较的结果应按从1～9的重要性排序。（3）检查和调整比较矩阵中的重要性指标，即测试一致性的可接受性。（4）利用线性代数的理论和方法，对收集所有比较信息的矩阵集进行处理，挖掘出深层次的、实质性的综合信息作为决策支持[5]。

这种方法既追求高等数学，又不注重行为、逻辑和推理。相反，它把定性方法和定量方法结合起来，对复杂系统进行分解，可以使人的思维过程数学化、系统化，易于被人们接受。将定量决策问题转化为多级、单目标问题，通过两两比较确定同级要素与上级要素之间的定量关系。最后，进行了简单的数学运算。计算简单，结果简单明了，便于决策者理解和掌握。

层次分析法（AHP）主要是基于评价者对评价问题的本质和要素的理解。它比一般的定量方法更具定性分析和判断能力。因为AHP是一种模拟人的决策过程的思维方式，它让大脑判断各要素相对重要性，保留人脑对要素的印象，并计算简单的权重。这一思想可以解决传统优化技术无法解决的许多实际问题。

层次分析的步骤：（1）建立指标体系的层次结构模型。应用层次分析法解决实际问题，首先明确要分析的目标问题，然后分析其影响因素，并根据影响因素的一定顺序，对层次结构进行排序。（2）构造判断矩阵。系统各要素之间存在一定的层次关系。判断和比较每个元素在同一水平上的相对重要性。相对重要性用适当的尺度表示。为了确定判断矩阵的值，通常要求许多专家反复比较两个因素哪一个更重要，并按照1～9重要度来分配值。（3）确定权重。权重是根据最大特征值所对应的特征向量确定的，对最大特征值的特征向量进行归一化所得到的就是各个因素的权重。（4）一致性检验。当被比较的元素是模糊的和复杂的时，通常不可能保证判断矩阵是完全一致的。在这种情况下，判断矩阵的最大特征值大于矩阵的阶数，并且还有其他非零的特征值。如果使判断矩阵的最大特征值接近矩阵的阶数，而其它特征值接近于0，则可以使判断矩阵具有令人满意的一致性，从而进一步保证结果的合理性。因此，为了判断矩阵的一致性是否满足要求，有必要对其进行一致性检验。

2 加油站选址

2.1 建立结构模型

加油站因类型不同，涉及的选址因素也各不相同。加油站选址的决策取决于经济因素、安全环保因素、加油量因素和政策因素。其中政策因素是任何类型加油站都必须要符合的，对任意类型加油站都很重要，加油量因素中的单车加油量因素对于候选地址来说不容易确定，单车加油量因素与用户习惯、个人经济情况等随时变化因素决定，因此政策因素和单车加油量因素对不同候选地址重要程度相同本文不予考虑。

经济因素分为城市商业购物区、城市主要干道、国道线、城市交叉路口及出入口和高速出入口五个决策层要素；安全环保因素分为空旷，通风良好、周围无明火作业工厂、尽量靠近市区人多的地方，保证工作人员的人身安全、周围绿化好、有良好的排水排污系统、远离河流和农田、周围是否有居民区，尽量避免噪声污染六个决策层要素；加油量因素分为总车流量、有效车流量、入站率和单车加油量三个决策层要素[6]。

其中总车流量受区域状况、位置状况、未来规划状况、道路的重要程度、道路自身状况的影响。有效车流量受隔离带、双向车道数、服务道、车速、转向限制的影响。入站率受能见距离长短、遮挡性、进出加油站的方便性、附近加油站的密度、附近单位和个人拥有车辆情况的影响[6]。评价体系如图1所示：

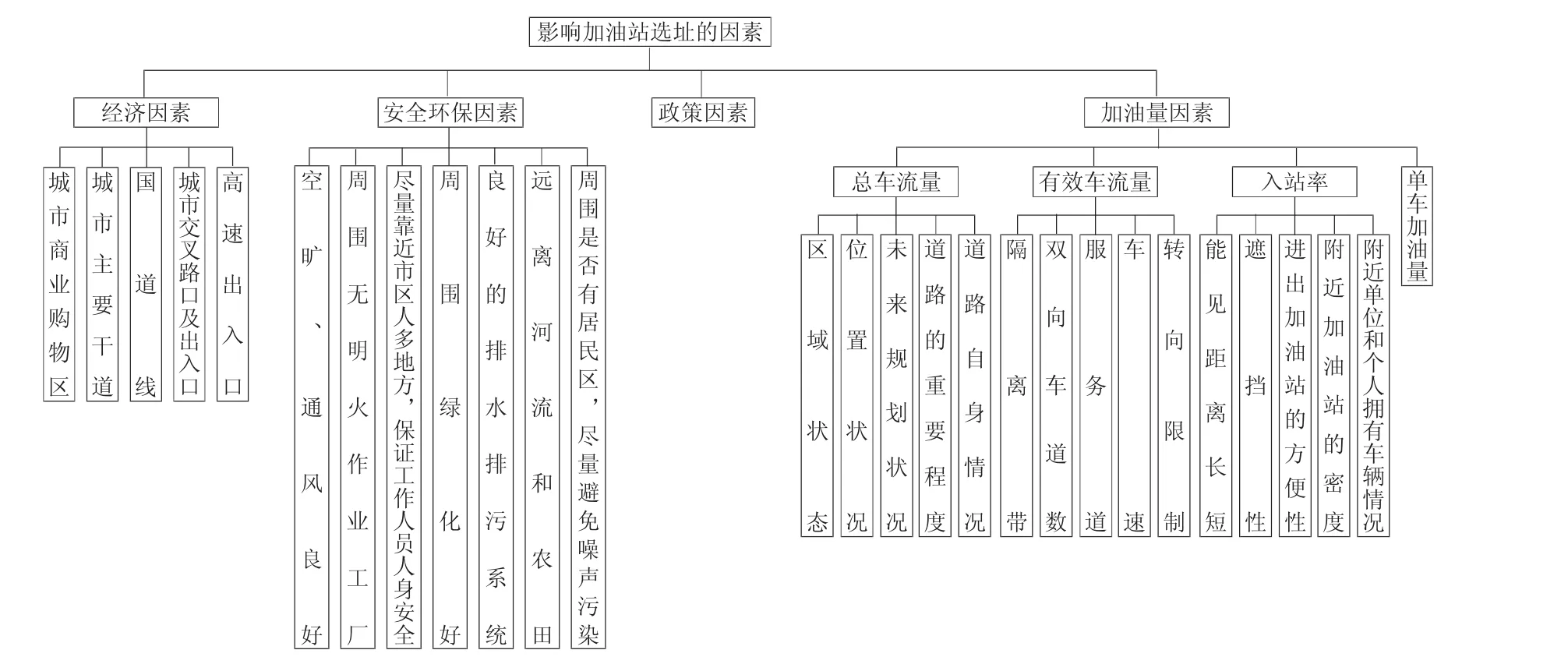
图1

2.2 构造判断矩阵

因为IMF的总部在美国，业务遍及全球，所以拉加德常年过着空中飞人的生活，她的一周像是普通人的一年，在欧洲见客户，去纽约开会，到芝加哥吃晚餐……连倒时差的时间都没有，但无时无刻她还能保持着清醒，还能兼顾打扮自己。拉加德说：“我总是自己化妆，但我每周会让一个理发师帮我打理一次头发，好让我保持形象。我一般选择不太容易起皱的裙和织物类服装，样式要简洁大方，要和我的职位相配。我身高有1米8，穿42号的鞋，所以我需要注意服装的平衡感。我喜欢赶时髦。我父亲曾是出色的服装设计师，在我童年时代，我见过他缝制出很棒的裙子，这些记忆让我知道怎么用不多的钱去塑造高贵的形象。”

2.3 一致性检验

一致性检验即是对所构造的矩阵是否可接受进行分析。当矩阵具有完全一致性时，最大特征值和矩阵的阶数（λmax=n）相同，其他特征值为0；当矩阵具有满意的一致性时，最大特征值近似于n，其他特征值近似于0，因此结果基本合理。主要依靠CI、RI、CR这三个参数指标来检验一致性的准确性，矩阵CR为一致性指标。

利用一致性指标CI、随机一致性指标RI和一致性比率CR做一致性检验。如果计算得到的CR值小于0.1，通常假定判断矩阵具有令人满意的一致性；否则，如果它大于0.1，则表明在比较或判断过程中可能存在一些矛盾。此时，对判断矩阵进行调整和修改，并对调整后的矩阵进行处理。通过上述步骤计算一致性，直到CR值小于0.1，停止调节工作。最后得到的符合满意的一致性要求的权重就是层次的单排序权重。计算公式如下：

表1 平均一致性指标RI标准值

经计算CI,CR的值如表2所示。

因为各矩阵随机一致性比率CR值均小于0.1，则矩阵通过一致性检验，该矩阵具有满意的一致性。

3 实例分析

通过评价指标按标准给四个候选地进行打分，各指标的评价等级为 ｛很好，好，一般，差，很差 ｝，对应的评分集为｛100,80,60,40,2｝。

表2 判断矩阵CI,CR值

3.1 三级指标评价

同理得D32= ［ 84.18 67.29 81.25 78.53］，D33= ［ 72.51 78.53 81.96 72.75］。

3.2 二级指标评价

同理得D22= ［ 80.63 76.77 72.83 75.96］，D23= ［ 78.12 73.53 79.14 74.20］。

3.3 一级指标评价

由二级评价可得D21,D22,D23，则一级指标评价矩阵为由权重H1= ［ 0.2493 0.5936 0.1571］T，因此D1= ［ 81.49 76.45 75.81 76.84］。

结论：根据四个候选地的得分，最高分一号为81.49，因此一号为四个备选地中最佳地址。

4 总结

本文采用层次分析法（AHP）对加油站的选址进行了研究。充分发挥AHP在多准则问题处理中的优势。对各因素在加油站选址中的重要性进行了排序，为进一步的工作提供参考。在应用时，要充分考虑实际情况，并根据专家的建议提出解决方案。层次分析法（AHP）将研究对象看作一个系统，按照分解法、比较判断法和综合思维法进行决策。它已成为系统分析和统计分析后发展起来的系统分析的重要工具。系统的思想是不要切断各种因素对结果的影响，而层次分析法中各层的权重最终将直接或间接地影响结果，并对各层次中各因素对结果的影响进行量化，非常清晰，而且各层次对结果的影响程度也不同。该方法特别适用于非结构系统和多目标、多准则的评价。相比之下，层次分析法是一种简单、实用、工作量小和方便的方法，能更好地解决加油站选址问题，具有一定的应用价值和实际意义。