离散需求下的药品库存控制模型研究
2018-12-20陈桂芳石荣丽广东药科大学广东广州510006
陈桂芳,石荣丽 (广东药科大学,广东 广州 510006)
1 研究背景
药品作为特殊商品之一,其供销的管理不仅影响着医药企业的运营发展,更与人们的健康息息相关。随着医药卫生体系改革的不断深入,医药费用居高不下,药品价格体系混乱,药品流通效率低下等问题越来越突出。为此,政府先后推出了《关于印发推进药品价格改革意见的通知》、《国务院关于印发“十三五”深化基药卫生体制改革规划的通知》、《关于在公立医院医疗机构药品采购中推行“两票制”的实施意见(试行)》等文件,分别从药品价格、药品流通等方面对药品进行管制。然而这些政策的实施并不能有效解决“看病难、看病贵”、药品价格虚高等问题。我国现有的医药企业约有8 000多家,市场竞争尤为激烈。药品价格的决定是由政府和市场共同合作来完成的,而影响药品价格主要有两个因素:一个是药品的成本,包括药品的生产成本和研发成本等;另一个是物流成本,包括运输成本和库存成本等。研究表明[1],库存和运输是成本消耗最大的物流活动,其成本约占物流总成本的三分之一到三分之二之间。库存作为供求之间的缓冲器,一方面,使生产和物流更灵活;另一方面,保证产品对顾客的可得性。由此可见,面对政府政策的调控和市场的激烈竞争,对药品库存管理的研究有着重大的意义,优化药品库存结构、提高药品仓库有效利用率,才是医药企业降低成本、增加利润、提高市场占有率的关键因素。
2 相关文献综述
库存管理是许多行业运营绩效的核心,由于其在实践中的重要性,库存管理一直是运筹学研究的热点。从1915年Harris提出著名的经济订货批量公式(EOQ模型)开始,开创了库存模型理论的新时代。到了20世纪50年代,随着运筹学、数量统计学等理论的应用,对库存问题的研究也逐步形成了库存理论,称为“存储论”。1953年,Whitin T.M撰写了《库存管理的理论》;1958年,Arrow K.J.等撰写了《库存和生产的数学理论研究》;1959年,Moran P.A.P撰写了《仓储理论》。此后,库存理论变成了运筹学中的一个独立分支,并根据需求的数量特征,将库存管理模型分为确定性需求和随机性需求,并对不同需求的库存模型进行了广泛深入的研究。
2.1 确定性需求库存管理模型
从1915年Harris提出的EOQ模型开始,对于需求确定性的库存管理问题的研究已较为完善。Goyal[2]提出了一种确定需求率的有限范围库存问题的经济订单量的方法。Ghare P M,Misra R,Shah Y K和Tadikamalla P等学者[3-6]在EOQ模型基础上对易变质物品的库存管理问题做了不同程度的研究,在他们的研究中,需求被假设为常数。Zeng Y[7]推导了具有确定性需求的多级梯库存控制模型,并通过实例证明了2的整数幂的有效性。季金震[8]假设需求确定的情况下,建立由一个生产企业、一个配送公司和多个零售企业组成的多级供应链的多级库存模型,求得到成本最小化的库存控制模型的目标函数,使得整个供应链库存整体最优。唐飞[9]假设需求和生产率为固定常数,提出只生产一种产品时,采用零售商占主导的寄售库存策略,以减少供应商和零售商的总成本。赵英会[10]通过理论分析和定量分析,研究EOQ模型在中小制造企业中的优化和应用,该模型中需求量假设为已知常数。
2.2 随机性需求库存管理模型
对于随机性需求库存管理的研究,部分学者是在确定性需求库存管理研究的基础上进行的,并得到一定的成果。Goyal[11]在文献[2]的基础上提出了在一定需求变化的情况下改进库存问题最优解的方法,并通过算例说明了该方法的有效性。Chang等[12]在经典的EOQ模型基础上,研究部分短缺量和时变需求对经济订货批量的影响,并通过数值算例说明该库存模型的有效性。
此外,Karlin[13]提出一种动态库存模型,在该模型中,需求分布可随时期变化而变化。在连续的变化时期内,每个阶段的最优策略的特征是一个单独的临界值。Song等[14]提出了一个需求率随经济波动或者随产品生命周期变化而变化的库存模型,并求出了最优策略的一些基本特征。马士华[15]等分别考虑确定需求量和随机需求量的情况下,建立提前期随机的库存控制模型。刘天亮[16]假设弹性需求下,针对是否采用替代策略情况下分别建立库存模型并进行仿真研究。刘峥[17]等假设随机需求下,通过比较双渠道供应链下制造商和零售商的独立库存模型和联合库存模型的供应链成本,得到供应链联合库存模型成本更低。陈丹丹等[18]基于离散需求下,分别建立缺货点在前和变质点在前的两种库存控制模型,并求解出易变质物品的最优缺货点和最低库存总成本,得出变质点在前的库存总成本比缺货点在前要低的结论。
综上可见,无论是确定需求库存管理的研究还是随机需求库存管理的研究都已较为完善。但是,在随机需求的库存管理中,学者们对离散需求下的库存模型研究相对较少,且仍在不断发展和积累中。本文考虑药品需求为离散随机变量,建立离散需求下的药品库存模型,采用(s,S)库存策略和边际分析法,确定其最低总成本下的最佳订货点和最优库存量,从而实现优化医药企业库存管理的目的。
3 离散需求下的药品库存模型建立和求解
3.1 符号与假定
为了更好地完成医药企业的生产销售计划,减少资源的浪费,提高药品仓库的有效利用率,针对药品经营企业建模,模型假设条件如下:
(1) 药品需求量r为离散随机变量,可能取值为:r1,r2,r3,…,rn(ri<ri+1,i=1,2,…,n-1 ),且ri的分布律已知。需求量r的概率为P(r),且
(2)允许缺货,每周期初开始补货,补货能瞬时完成。
(3)C1为每次订购费用,包括运输费、保险费以及装卸费等;C2为单位药品存储成本;C3为单位药品缺货成本;k为药品单价;s为订货点;S为最大库存量。
(4) 采用(s,S)库存策略,即:当初始库存量为I,订货点为s,若I>s,则不对库存进行补充;若I≤s,则对库存进行补充,补充库存量为Q,Q=S-I,补充后达到最大库存量S,药品库存消耗途径如图1。

图1 药品库存消耗途径
3.2 模型的建立与最优解分析
本模型采用(s,S)库存策略,当I≤s时,需要对库存进行补充,库存量由I补充到S,此时,本周期总成本=订购成本+储存成本+缺货成本,其函数为:

在本周期的药品销售中,目的是求解出最经济的最大库存量S以及最佳订货点s,使得总成本C(s,S)期望值最小。由于需求量r是离散随机变量,是r1,r2,…,rn中的一个,因此订货点s和最大库存量S的取值也应是r1,r2,…,rn中的一个。令S=Si=ri(i=1,2,…,n),由于C(Si)是离散的,故采用边际分析法,考察 ΔC(Si):

由于(C1+C2)ΔSi>0且F(Si)是关于i的严格单调递增函数,因此 ΔC(Si)和[F(Si)-N]同号,且都是关于i的严格单调递增。由于缺货成本C3至少包括失去销售机会的损失,且售价一般高于成本,则有:
在实际销售中,一般P(r1)和P(rn)都比较小,设F(S1)=P(r1)<N,F(Sn-1)=1-P(rn)>N,即P(rn)<1-N。此时则有:

由于 ΔC(S1)<0,ΔC(Sn-1)>0,且 ΔC(Si)具有关于i的严格单调递增性质,由此可知,随着i的增加,ΔC(Si)先取负值,然后变为正值。即C(Si)随着i的增加,先减少,再增加,有最小值。因此,假设最优库存量S*为:S*=Si=,要求出最小C(Si)值,则C(Si)应同时满足不等式组:

将不等式(2)详细写出来得:

综合以上两式得:

确定最优库存量S*后,现要确定订货点s。当I>s时,不需要订货,此时,本周期总成本=储存成本+缺货成本,其函数为:
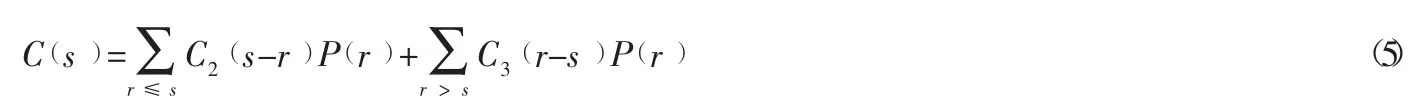
根据订货点s的意义,当周期初始库存量I=s时,不订货的期望总成本应当不超过订货的期望总成本。则订货点s应满足以下不等式:
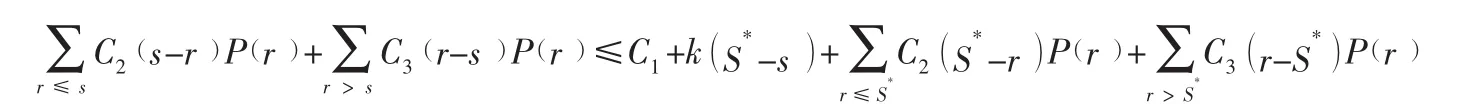
整理得:

当s=S*时,不等式(6) 明显成立,但根据最佳订货点s*的3个性质:①s*≤S*;②s*需满足不等式(6);③s*是所有满足不等式(6)中最小。由于需求为离散的随机变量,所以订货点s的取值也是r1,r2,…,rn中的一个,令s分别取值为:r1,r2,…,rn,按从小到大的顺序代入不等式(6)中,则第一个满足不等式(6)的ri为最佳订货点s*。
4 算例分析
假设药店销售某种药品,单价为30元/盒,订购费用为200元/次,每盒药品存储费用为10元/月,药品缺货成本为60元/盒,该药品每月需求率如表1,根据上述的药品库存模型,求出该药品最优的订购策略。

表1 药品需求概率表
设本周期初始库存量I=0≤s,将上述数据代入所建模型可得:
先计算:

再计算:

显然,左边>右边,公式(6) 不成立。
同理,再将s=50,S*=70代入公式(6) 得:
左边=3 185;右边=2 995,左边>右边,公式(6)仍不成立。
再将s=60,S*=70代入公式(6) 得:
左边=2 955;右边=2 995,左边<右边,公式(6)成立,所以最佳订货点s*=60,因此该药店应采取(s,S)=(60,70)的库存策略,即初始库存水平低于或等于60盒时,需要订货补充,最优补充量Q*=S*-I=70盒。
5 结论与讨论
本文提出了需求为离散随机变量的药品库存模型,从该模型的结构上看,推算出最低期望总成本下的最大库存量以及最佳订货点尤为关键,再根据实际初始库存量确定是否需要订货以及最优订货量,最后通过算例分析对该模型进行验证,得到该药品最低总成本的库存策略为(60,70)。由于本模型是采用(s,S)库存策略,所以在药品储存时可以分两堆存放,一堆数量为订货点s的量,其余放另一堆。平时取后一堆以满足需求,当取完后一堆,需要取前一堆时,则在周期末选择订货;如果到了周期末,前一堆仍未动用,则本周期不订货。采用此策略可以在实际盘点中更容易确定是否需要订货,从而提高工作效率。
