基于区间仿射响应面的非概率可靠性分析

2018-12-19孙静怡张建国彭文胜邱继伟谭春林

计算机集成制造系统 2018年11期

孙静怡，张建国，彭文胜，邱继伟，谭春林

(1.中国运载火箭技术研究院，北京 100076; 2.北京航空航天大学可靠性与系统工程学院, 北京 100191; 3.北京航空航天大学可靠性与环境工程技术国防科技重点实验室, 北京 100191; 4.北京空间飞行器总体设计部, 北京 100094)

0 引言

工程中对机械产品进行可靠性分析通常只能得到不确定性参数的分布区间[1]，当机械产品的极限状态函数无法用解析形式表达时，一般采用区间响应面法进行近似分析评估，例如：Sofi等[2]通过求解多项式响应面间的比例建立适用于区间及随机变量有限元分析的统一响应面框架，在不同不确定性模型下比较结构响应的变异性；唐忠等[3]构建了包含区间不确定性参数的二阶多项式极限状态函数代理模型，并提出一种基于偏弹性理论的可靠性分析方法。然而上述分析中的区间变量若在区间响应面函数中多次出现，则会引发区间运算结果扩张，影响计算结果的准确性。

针对这一问题，LI等[4]利用区间参数的二阶泰勒展开信息建立“具有边界约束的二次规划”模型，并利用凸函数算法差异降低区间扩张对结构特征值分析的影响；WU等[5]将原函数展开为chebyshev多项式后,再利用区间算法求解各单项式的值，最后求和计算原函数的扩张区间；方圣恩等[6]基于泰勒级数展开式分别建立参数与响应区间的函数关系，并通过构建反演问题分步识别参数区间，提高计算结果精度。上述研究均从改进响应面函数的角度出发，通过对函数进行变形或替换抑制区间扩张。然而该过程中由于函数关系复杂，导数求解困难等原因，在一定程度上增大了计算量。因此，相关研究者又提出一系列区间运算的改进算法，吕震宙等[7]通过比较变量边界值与中心值的相对误差，提出区间截断法；Alefeld 等[8]考虑所有输入区间变量端点的组合形式，提出区间组合法；郭书祥等[9]结合有限元分析，提出区间有限元法及响应的矩阵运算方法；邱志平等[10-11]对参数区间的中点进行泰勒展开，提出区间参数摄动法，并在分析区间有限元法不足的基础上，基于Chebyshev正交多项式提出配点型区间有限元法。虽然上述方法已提高计算精度，但仍存在一定误差，且随着研究对象复杂程度的增加更为突出。仿射理论[12]处理不确定性问题时，其运算规则具有优化性质，计算结果精确，特别对长计算链优势明显。谢永强等[13]等在函数上下界计算中引入矩阵形式的仿射计算公式，提出一种改进仿射算法，减小了不确定系统响应界的分析误差；Zou等[14]基于改进的仿射算法，融合泰勒展开提出泰勒—仿射算法(Taylor Affine Algorithm, TAA)用于分析计算结果的不确定性；姜潮等[15]利用仿射坐标，将相关变量转换为独立变量，提出一种考虑相关性的概率—区间混合不确定性模型及结构可靠性分析方法。目前，仿射理论已拓展至非概率可靠性领域，但多依赖于显式极限状态函数，限制了该方法的应用。

本文利用仿射理论提出一种区间仿射响应面方法(Interval Affine Response Surface Method, IARSM)来抑制区间扩张。该方法首先对区间参数进行仿射变换，利用线性回归得到区间仿射响应面；然后，利用区间边界的分割组合构建响应面更新及求解机制，进一步提高基于区间仿射响应面的非概率可靠性指标计算精度。

1 区间扩张问题及仿射理论

1.1 非概率可靠性指标求解中的区间扩张问题

不确定性参数可用区间变量X=[XL,XR]表示，XL，XR分别为区间变量的下界和上界。对于含有k个区间参数的机械产品，极限状态函数的一般形式为

M=g(X)=g(X1,X2,…,Xk)。

(1)

(2)

(3)

当极限状态函数M为X各分量的连续函数时，其值域也为区间变量，记为M=[ML,MR]。非概率可靠性指标

(4)

式中Mc及Mr分别为极限状态函数响应区间的均值和离差。

若η>1，表明产品处于安全状态，且η值越大，安全程度越高；若η<0，则表明产品失效；若η∈[0,1]，则表明产品存在失效危险。

实值极限状态函数f(x)定义为从实数集Rn映射到R，其对应的区间极限状态函数g(X)(IR→IR)为包含函数在其定义域区间X上所有映射的“外壳”[17]，满足

g(X)=[{f(x)|x∈X}]。

(5)

通常情况下，由区间函数计算结果组成的外壳并不唯一，区间函数的结果比实际结果的范围更大：

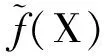
⊆g(X)。

(6)

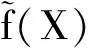
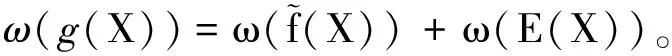
(7)

如图1所示，相比于实值极限状态函数f(X)，在相同的定义域内，g(X)的值域区间宽度增大，利用该结论求解得到的非概率可靠性指标为

(8)

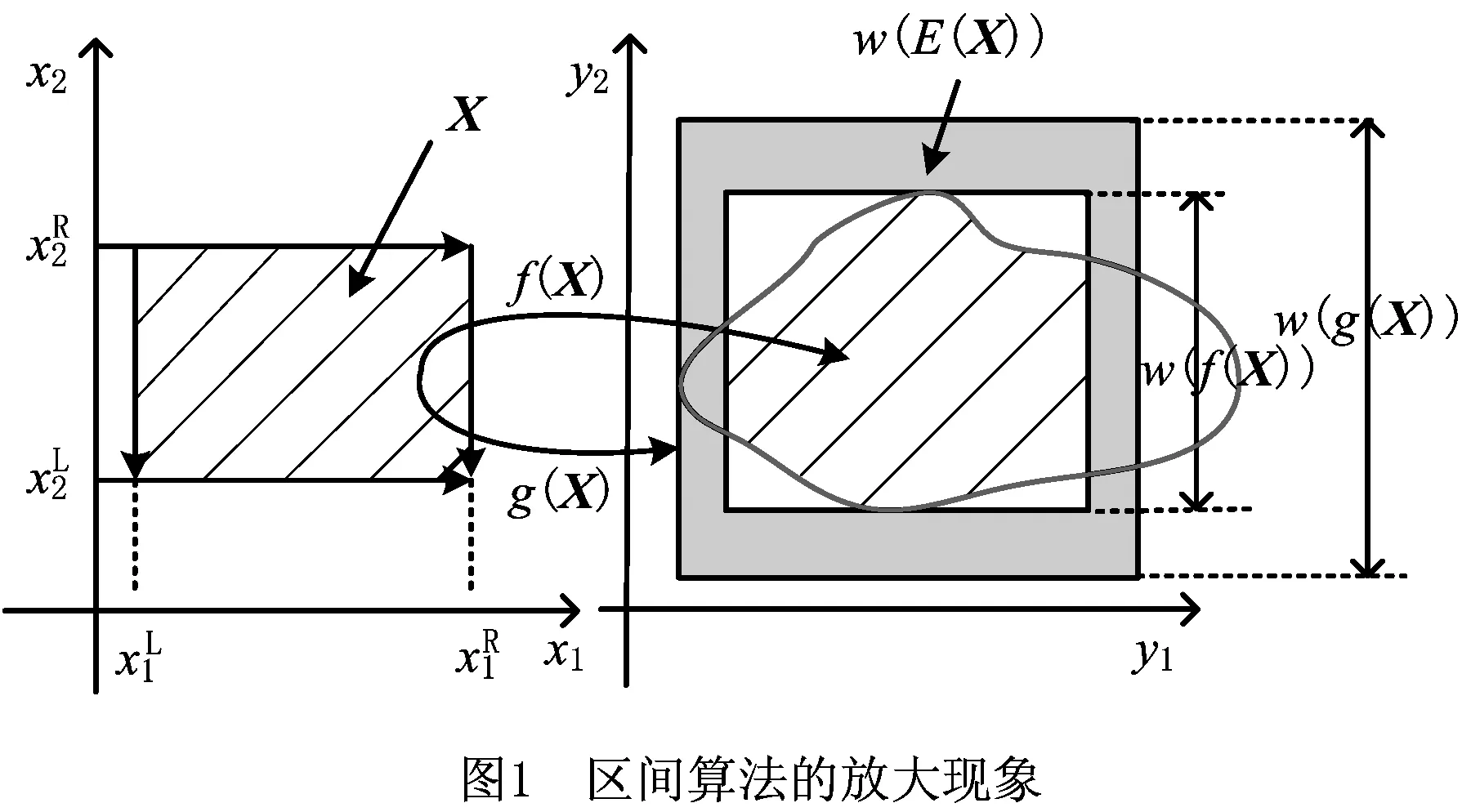
由式(7)和式(8)可知，计算得出的可靠性指标η′中含有误差项ω(E(X))，导致非概率可靠性指标的计算结果精度下降，丧失实用价值。

1.2 仿射理论

不确定性参数Y的仿射形式可表示为[18]

[Y]=y0+y1ε1+y2ε2+…+ynεn。

(9)

式中：y0为仿射形式的中心值；εi(i=1,2,3,…,n)为噪声元，εi的值未知，范围在[-1,1]之间，当ε1=ε2=…=εn=±1时，Y取得最大和最小值；yi为浮点实数，决定了噪声元的大小。因此，可得[Y]的区间形式为

(10)

区间参数X=[XL,XR]对应的仿射形式为

(11)

对于[A]=a0+a1ε1+a2ε2+…+anεn和[B]=b0+b1ε1+b2ε2+…+bnεn两个仿射形式的变量，运算规则定义为：

[A]±[B]=(a0±b0)+(a1±b1)ε1+

(a2±b2)ε2+…+(an±bn)εn;

(12)

(13)

式中εk为乘法运算中产生的新噪声元。

2 区间仿射响应面方法

2.1 区间仿射响应面建模

基于变量为区间参数的多项式响应面模型为：

(14)

式中：Xi为区间变量；β0,βi,βii(i=1,2,…,k)为待定常系数。

对式(14)中的区间参数进行仿射变换：

(15)

(16)

式中：

(17)

(18)

(19)

(20)

对比式(14)和式(16)可知，响应面函数转化由2k+1个不同的噪声元构成的线性函数，所有变量在响应面函数中仅出现一次，因此可有效抑制区间扩张。

区间仿射响应面模型中共有2k+1个待定系数λ。因此，进行实验设计时，应根据实际情况选择合适的试验设计方法，在自变量取值范围内选取2k+1个实验点，实验点对应的噪声元大小为

(21)

式中xi为选取的实验点，xi∈Xi。

利用仿真分析得到产品实验点处的响应值gi，与对应噪声元向量形成构建区间仿射响应面的样本集{εi,gi}(i=1,2,…,2k+1)，在此基础上，通过线性回归的方法依据式(22)求解待定系数：

λ=(P(ε)T·P(ε))-1·P(ε)T·

[g(ε1),g(ε2),…,g(εn)]T。

(22)

式中：λ=(a0,…,ai)为多项式待定系数，P(·)为参数矢量矩阵。

基于该模型，得到在所求解区间范围内，响应面输出的响应区间[g]及对应的非概率可靠性指标η[g]：

(23)

(24)

2.2 基于IARSM的非概率可靠性分析方法

为获得更为准确的响应面计算结果，本文借鉴区间分割法的区间边界组合思想[19]，建立模型更新及求解机制，并利用输出响应求解非概率可靠性指标。

模型更新及求解机制的主要思想是将区间自变量Xi划分为宽度相等的Nd个子区间，其中第j(j=1,2,…,Nd)个子区间的范围为

(25)

构建子区间IARSM求解响应，搜索全局最优值作为输出，实现响应面迭代更新。寻优过程的优化模型为：

min/max [g(ε)]。

s.t.

εi∈[-1,1]，i=1,2,…,k;

εi+k∈[0,1],i=1,2,…,k。

(26)

随着Nd的增大，对于任意xi∈Xi,均有Xij与其对应，且{f(x),x∈Xij}→g(Xij)，实值极限状态函数的解区间与区间极限状态函数趋于一致，进一步减小ω(E(X))。

基于IARSM进行非概率可靠性分析的步骤如下：

步骤1根据目标产品性能及特点建立可靠性极限状态函数的一般形式，识别函数中的区间变量X=(X1,X2,…,Xk)。

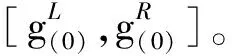
步骤3激活响应面更新及求解机制，对响应面输出结果进行迭代更新：

(1)根据精度要求，设定收敛条件ζ，置d=1。

(2)分解Xi的给定区间，形成宽度相等的Nd个子空间Wt={R1,R2,…,RNd}，Nd=int(1.5Nd-1)(一般情况下，首次区间划分个数为函数区间变量个数k，即N1=k)。

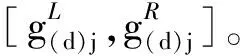
(5)选取第j1，j2个区间进行局部优化，得到该子区间上的最大、最小值g(d)j1,g(d)j2。

(27)

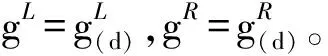
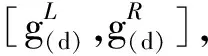
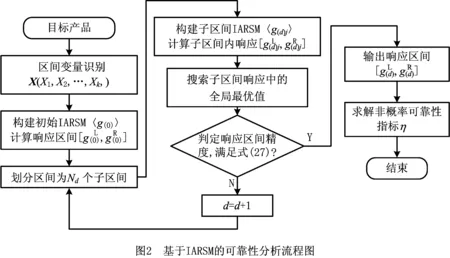
基于IARSM进行非概率可靠性分析的流程图如图2所示。

3 案例分析

3.1 数值案例

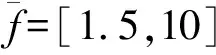
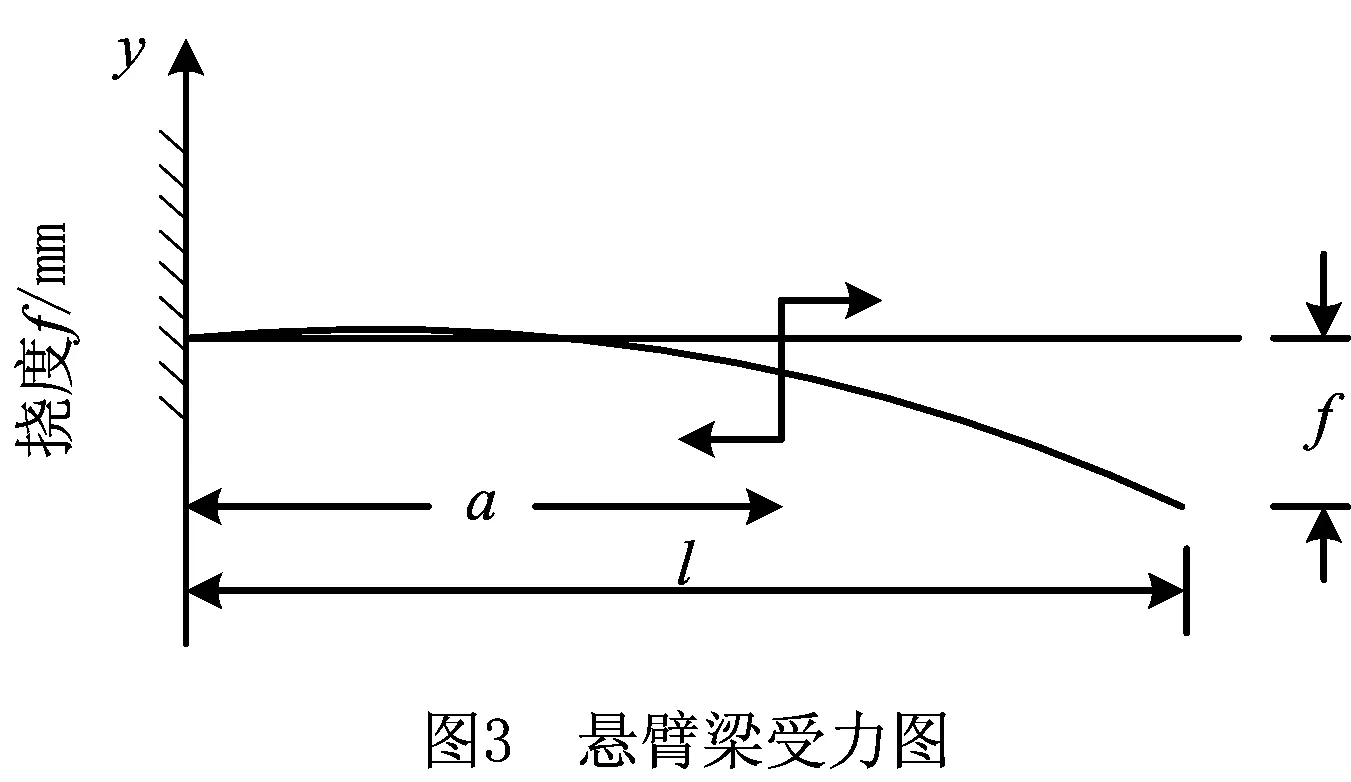
根据材料力学知识可知，悬臂梁的挠度f与所给参数的函数关系式为

(28)

将M,a的取值区间代入式(28)，运用区间运算

求得f=[1.312 5,7.031 5] mm。

下面，将该结构作为“黑盒”，运用本文方法求解响应区间。依据式(16)，构建挠度f的初始区间仿射响应面

f=f0+f1ε1+f2ε2+f3ε3+f4ε4。

(29)

式中fi(i=0,1,…,4)为待求未知量。

采用中心复合设计法，在M,a的区间范围内抽取9组实验点，并利用机械系统动力学自动分析(Automatic Dynamic Analysis of Mechanical Systems, ADAMS)系统进行运动学分析。实验点集合仿真结果如表1所示。

表1 运动学仿真结果

依据式(17)和式(21)可得实验点集合所对应的噪声元矩阵

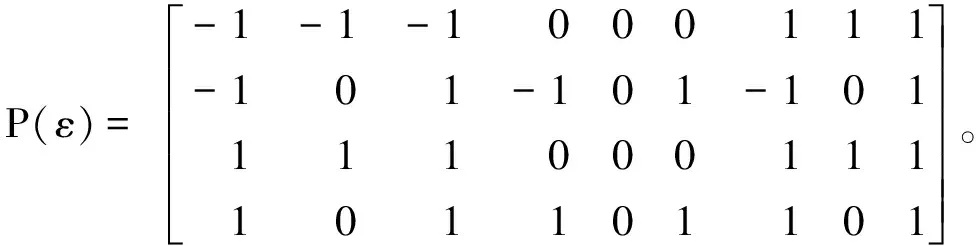
对噪声元矩阵及悬臂梁的挠度进行数据拟合，得到摇杆角位移的区间仿射响应面

[f]=3.500 0+1.468 8ε1+0.437 5ε2+

0.000 1ε3-0.109 4ε4。

(30)

如图4所示，利用该响应面求得挠度f的初始响应区间f=[1.484 2,5.406 3]。

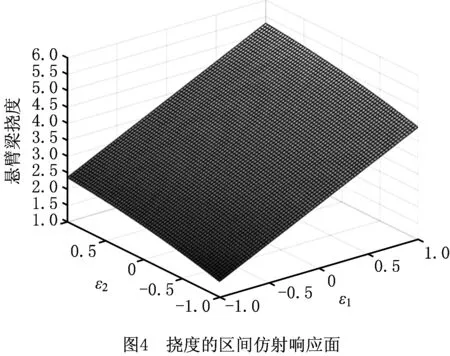
激活IARSM更新及求解机制，对输入区间变量进行区间划分，并设定收敛条件ζ=0.01。经过6次迭代后，ζ=0.008 9<0.01，结果收敛，响应面最终输出的响应区间f=[1.574 0,5.314 2]。

为验证响应面的计算结果精度，本文利用基于区间分析的Monte Carlo方法[20]进行仿真求解，并将该结果作为基准，定义区间宽度的相对误差

(31)

式中：ω(gMC)为利用蒙特卡洛方法求得的真实响应区间宽度，ω(g)为利用其他方法求得的响应区间宽度。

同时，将区间仿射响应面法同区间运算、区间截断法、区间组合法进行对比，计算结果如表2所示。

表2 计算结果对比表

由表2可知，利用式(28)进行区间运算所得的结果产生区间扩张，宽度相对误差达55.36%，而本文所提出的区间仿射响应面法经过更新后得到的响应区间在分布范围上接近真实值，宽度相对误差仅为1.60%，相比之下，对区间扩张的抑制程度较高。由式(7)和式(8)可知，基于该方法求解出的非概率可靠性指标中，误差项ω(E(X))=0.059 0，比区间运算中的ω(E(X))=2.037 8小。因此，区间仿射响应面法对区间扩张问题处理效果较好，计算得出的非概率可靠性指标结果精度较高。

依据传统应力—强度干涉模型，构建悬臂梁极限状态函数的区间仿射响应面

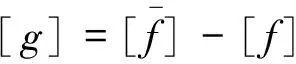
(32)

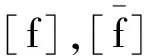
基于该响应面求解非概率可靠性指标

(33)

由计算结果可知，η≈0.376 8<1。因此，在不确定参数区间范围内，悬臂梁存在失效危险。

3.2 工程案例

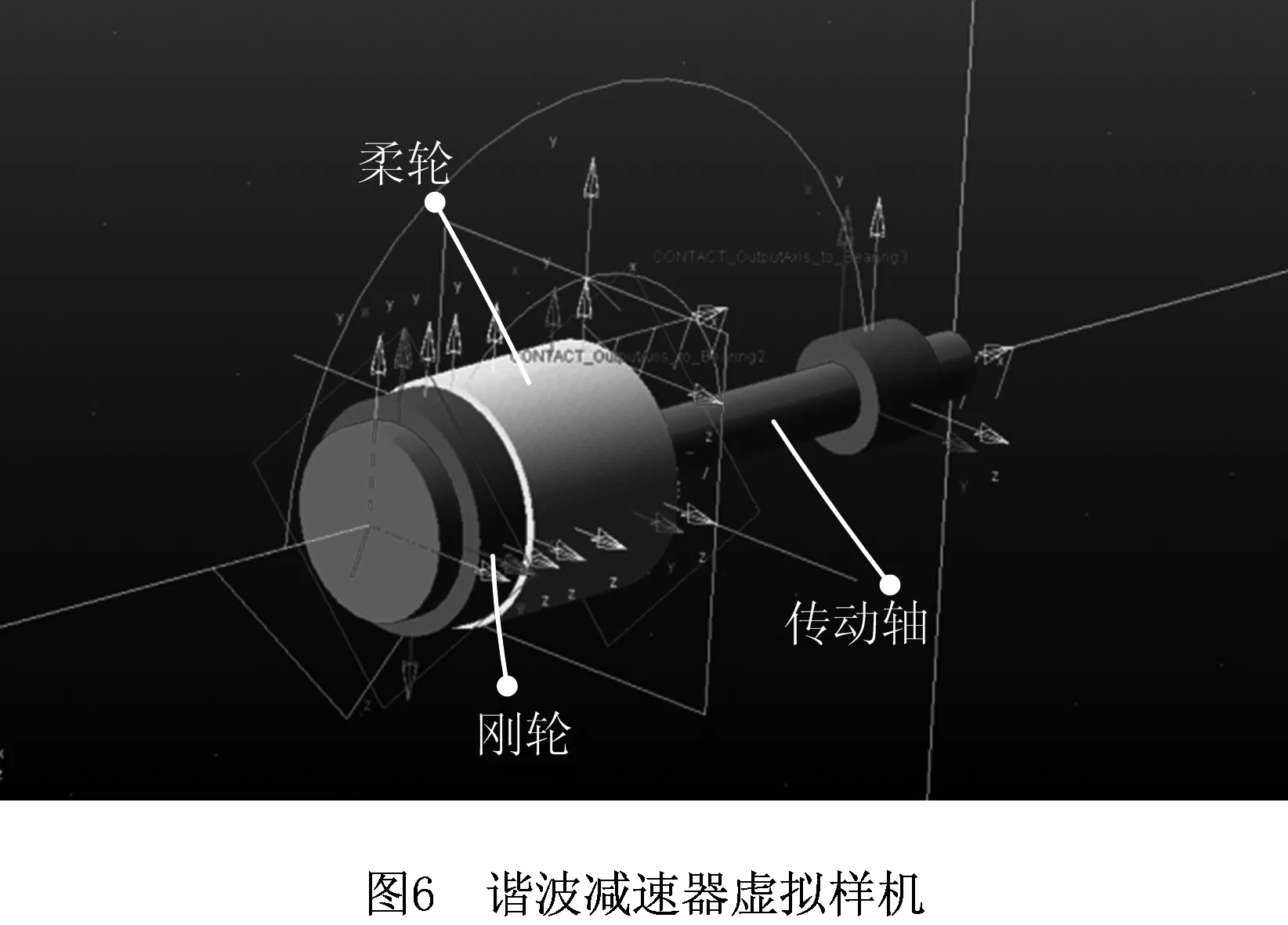
谐波减速器是一种以薄壳弹性变形为理论基础的新型机械传动装置，主要由波发生器、柔轮、刚轮3部分组成。谐波齿轮传动是在波发生器作用下，迫使柔轮产生变形，并与刚轮相互作用而达到传动目的，如图5所示。

传动误差是衡量谐波减速器传动精度的重要指标之一。虽然减速器传动误差可通过理论计算确定，但由于影响因素较多且函数关系复杂，理论计算结果精度较低且计算量巨大。同时，目前谐波减速器的传动误差大多仅考虑由部件加工、装配引发的静态误差，未考虑高频情况下柔轮柔性和机构摩擦引起的滞回误差对传动精度的影响。因此，本文利用所提方法对电机不同转速下谐波减速器的传动误差进行分析。

首先，分析波发生器输入角为50°时，谐波减速器在两种情况下的传动误差。谐波减速器的传动误差定义为在一定转速条件下柔轮理想输出位置和实际输出位置之差Δθ,

(34)

式中：θm为波发生器输入角位置，θl为柔轮输出角位置，N为谐波减速比。

利用ADAMS构建谐波减速器虚拟样机，如图6所示，模型中影响传动精度的确定性参数设定如表3所示。

表3 谐波减速器动力学模型确定性参数

3.2.1 低频情况(电机转速为1 r/min)

此时传动误差主要为静态误差θp，影响静态误差的各项不确定因素及取值情况如表4所示。

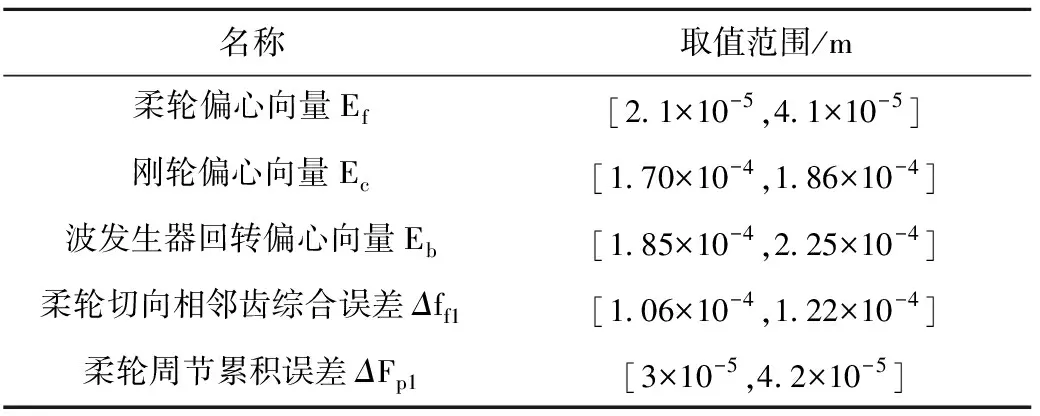
表4 谐波减速器静态误差不确定参数

选用BBD(Box-Behnken)实验设计法对以上参数进行实验设计并仿真，传动误差Δθp的区间仿射响应面

[Δθp]=θm/N-[θl]=50/90-0.559 06+

5.23×10-5ε1-8.13×10-5ε2+3.31×10-5ε3-

1.82×10-4ε4-4.36×10-5ε5+1.34×10-5ε6+

5.62×10-5ε7-3.78×10-5ε8+

5.61×10-5ε9+3.25×10-5ε10。

(35)

激活模型更新机制，经7次迭代后，传动误差区间满足收敛条件Δθp=[-0.003 90,-0.002 92]。此时，传动误差主要来源于静态误差，为进一步研究滞回误差对传动误差的影响，利用本文方法对高频情况下谐波减速器的传动误差进行分析。

3.2.2 高频情况(电机转速为100 r/min)

此时传动误差受静态误差和滞动误差共同影响，进行传动误差分析时，需同时考虑表4和表5中的不确定因素。选取所有区间变量均取中值的样本点带入模型进行仿真，传动误差变化情况如图7所示。

表5 谐波减速器滞动误差不确定参数

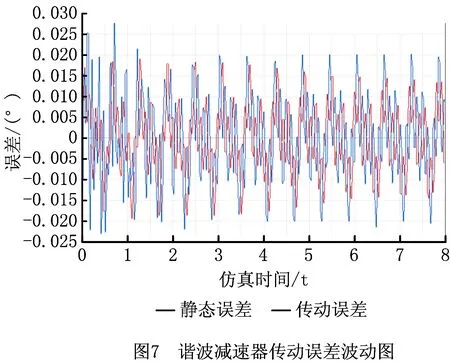
利用本文方法构建区间仿射响应面,求解传动误差θ：

[Δθ]=θm/N-[θl]=50/90-0.560 15+

4.19×10-5ε1-5.35×10-5ε2+2.92×10-5ε3-

1.21×10-4ε4-3.84×10-5ε5+5.11×10-5

ε6-4.43×10-5ε7-1.83×10-5ε8+3.59×10-5

ε9+3.72×10-5ε10+6.30×10-6ε11+

3.86×10-5ε12-3.38×10-5ε13-2.81×10-6ε14+

8.32×10-5ε15-3.75×10-6ε16+3.26×10-6ε17+

2.81×10-6ε18-1.39×10-5ε19+4.76×10-5ε20。

(36)

激活模型更新机制，经12次迭代后，传动误差区间满足收敛条件Δθ=[-0.005 07°,-0.003 89°]。

由图7可以看出，谐波减速器开始运行时，由于电机起步运行不稳，导致传动精度及静态精度波动较大;随着电机逐渐稳定，两类误差均呈周期性波动。同时，运动过程中，传动误差均大于静态误差，多出的部分即为滞回误差对传动误差的影响。利用本文方法得出的误差区间也印证了上述结果。误差结果的符号表示误差方向，绝对值为误差大小。对比两误差区间中的最大传动误差，综合考虑静态误差及滞回误差的传动误差(0.005 07°)比仅考虑静态误差时(0.003 90°)大0.001 17°，相比增加23.1%，因此在对谐波减速器进行传动误差分析时，有必要考虑柔性和摩擦的影响。

将本文方法与ADAMS进行联合仿真计算，得出电机稳定后，谐波减速器周期性传动误差带，如图8所示。

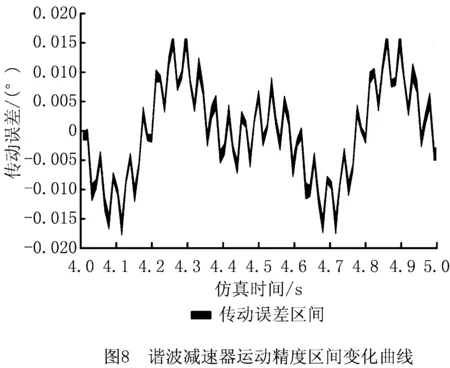
由图8可知，谐波减速器在循环周期内的传动误差区间为[-0.018 76°,0.017 98°]，根据设计要求，谐波减速器的传动误差阈值为0.02°，此时η=1.109 9，满足可靠性要求。

为进一步验证本文方法的计算精度，利用如图9所示的谐波减速器运动精度测试平台对不同电机转速时的传动误差进行测试，并与本文计算结果进行比较。平台采用恒温箱封闭，电机输入端与谐波减速器输出端分别连有角速度和角度传感器，测定输入和输出端的角速度与角位置。对比结果如表6所示。

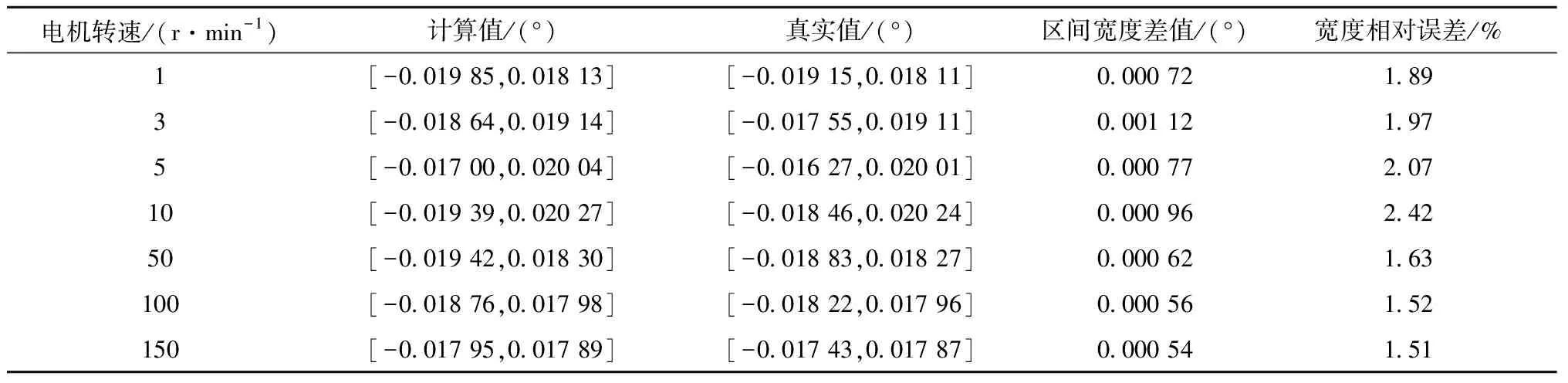
电机转速/(r·min-1)计算值/(°)真实值/(°)区间宽度差值/(°)宽度相对误差/%1[-0.019 85,0.018 13][-0.019 15,0.018 11]0.000 721.893[-0.018 64,0.019 14][-0.017 55,0.019 11]0.001 121.975[-0.017 00,0.020 04][-0.016 27,0.020 01]0.000 772.0710[-0.019 39,0.020 27][-0.018 46,0.020 24]0.000 962.4250[-0.019 42,0.018 30][-0.018 83,0.018 27]0.000 621.63100[-0.018 76,0.017 98][-0.018 22,0.017 96]0.000 561.52150[-0.017 95,0.017 89][-0.017 43,0.017 87]0.000 541.51

通过表中数据可以看出，两种情况下，实验得到的误差值与计算结果均比较接近，宽度相对误差在1.5%～2.5%范围内，考虑到相关参数的不确定性，相对误差在接受范围之内，由此可见本文方法求解精度满足工程要求。根据上述结果求解谐波减速器正常运行条件下随电机转速变化的可靠性指标，如图10所示。

由图10可知，两条曲线吻合度较高，可靠性指标—转速曲线呈先下降再上升的趋势，主要是由于相同环境条件下，谐波减速器可靠性指标与磨损量有关，磨损量与接触载荷比和转速的乘积成正比。当转速小于10 r/min时，随着转速的升高，接触载荷比下降的速率较大，但接触载荷比和转速的乘积却逐渐增大，因此磨损量增大导致可靠性指标下降;当转速大于10 r/min时，随着转速的升高，接触载荷比减小较慢，尤其当转速大于100 r/min时，接触载荷比已趋于0，接触载荷和转速的乘积逐渐减小，因此可靠性指标上升。根据传动精度可靠性指标在工作空间内的变化趋势，设计者应在设计期间考虑柔轮柔性和摩擦对传动精度的影响，同时根据任务需求合理选择电机转速，控制传动误差在可接受范围内，从而提高谐波减速器的传动精度。