基于支持向量数据描述的剩余寿命预测方法
2018-12-19武千惠黄必清
武千惠,黄必清
(清华大学 自动化系,北京 100084)
0 引言
设备故障不仅产生了大量的维修费用,降低了生产效率和经济效益,还会引发安全事故,造成人员伤亡。为了提高设备可靠性、保证人员安全、提高企业生产效率,确定维修保障资源、做出合理的维修决策十分重要。预测性维修是目前最为理想的维修策略[1]。预测性维修指在设备运行时对目标部件进行状态监测,判断运行状态并预测未来的发展趋势,依据可能的故障时间制定维修计划,安排维修活动。预测性维修的核心在于故障预测,通常基于剩余寿命预测技术实现[2-3]。
目前,故障预测方法主要分为:基于模型的预测方法,基于经验的预测方法和数据驱动的预测方法[1,4]3大类。基于模型的方法通过应用物理定律建立一组代数方程或微分方程作为预测模型,利用该模型表示退化现象(如变形、裂纹和腐蚀)。由于设备部件的退化过程通常都是非线性的,且与不确定的工况密切相关,因此该类方法的应用场合十分受限。基于经验的预测方法利用经验反馈数据(如失效时间)调整一些分析模型(如威布尔分布、指数分布)的参数,通过这些参数模型估计系统的失效时间或剩余寿命,但往往存在预测精度不够理想、过度依赖知识和经验等问题。数据驱动的故障预测方法不需要依靠物理参数(如工况、材料性质),就可以通过传感器状态监测数据建立预测模型。与基于模型和基于经验的方法相比,数据驱动的预测方法在预测准确度、计算复杂度和可推广性等方面进行了折中,具有更强的可操作性。本文研究内容即为数据驱动的故障预测方法。
研究人员在数据驱动的故障预测方面做了许多工作,主要包括人工神经网络(Artificial Neural Network, ANN)[5-7]、隐马尔可夫模型(Hidden Markov Model, HMM)[1,8]、贝叶斯信念网络(Bayesian Belief Network, BBN)[9]、支持向量机(Support Vector Machine, SVM)[10-11]和支持向量数据描述(Support Vector Data Description, SVDD)[12-14]等方法。例如,神经网络方面,Huang等[7]以轴承的退化期为研究对象,首先利用自组织映射(Self-Organizing Maps, SOM)神经网络生成的最小量化误差(Minimum Quantization Error, MQE)训练BP神经网络,然后通过失效权重适用(Weight Application to Failure Times, WAFT)技术构建了剩余寿命预测模型。马尔可夫模型方面,Tobon-mejia等[1]提出一种基于高斯混合隐马尔可夫模型的预测方法,模型的隐状态代表设备在失效过程中经历的退化状态,剩余寿命可由每个退化状态的逗留时间直接计算得到。贝叶斯置信网络方面,Zhang等[9]提出一种利用高斯混合贝叶斯置信网络识别轴承退化状态,由退化状态识别结果随时间的变化预测剩余寿命的方法。由于设备的故障数据十分有限,基于神经网络、隐马尔可夫模型和贝叶斯置信网络的预测方法在实际应用受到了很多限制,主要表现为容易出现过拟合、模型稳定性较低、难以得到比较理想的预测结果等。
支持向量方面,陈斌等[12]针对转子振动台的不平衡故障预测问题,为不同的故障程度建立了不同的SVDD超球体,通过待测样本到各超球体球心的相对距离确定其所属的故障等级。因为随着故障等级的增加,相对距离的方向具有指向性,所以可将其作为预测不平衡故障程度的准则。Shen等[14]考虑轴承性能退化及动态信息的随机性和强模糊性,提出一种基于模糊SVDD和运行时间的单调性能退化评估指标,以有效刻画轴承损伤情况随工作时间的变化。Kim等[10]以轴承为研究对象,将其退化过程分为6个阶段,利用“一对一”多分类SVM方法进行故障分类,通过训练数据的分类情况求得轴承处于各个阶段的概率,最后利用轴承的工作时长和概率值预测剩余寿命。已有的基于支持向量的预测方法虽然能够对离散的目标部件的工作状态进行判断及预测,但存在难以预测连续的剩余寿命时长(如文献[12-14])或剩余寿命预测精度不够(如文献[10-11])等问题,应用于运维策略优化等后续工作时存在困难。针对以上问题,本文提出一种基于SVDD的剩余寿命预测方法。
1 基本方法
1.1 支持向量数据描述
给定数据集{xi,i=1,2,…,N},SVDD的优化目标为寻找在特征空间包含所有样本点的半径最小的超球面[15]。令c为超球面的中心,R为超球面半径,该优化问题可以表示为如式(1)所示结构风险最小化问题:
s.t.
(xi-c)T(xi-c)≤R2,i=1,2,…,N。
(1)
当训练样本中存在远离其他普通样本点的奇异点时,利用式(1)得到的超球面因包含大片空白区域而不能准确描述训练样本。为了提高算法鲁棒性,引入松弛变量ξi和惩罚因子C,以在最小超球面半径和最小非目标样本分类误差间寻求折中。C越大,上述奇异点对目标函数的影响越大,此时原问题转换为:
s.t.
(xi-c)T(xi-c)≤R2+ξi,ξi≥0,i=1,2,…,N。
(2)
构造Lagrange函数
αi≥0,γi≥0;
(3)
对L求偏导并令其等于0,有
(4)
将式(4)带入式(3),得到仅包含Lagrange乘子的原问题的对偶问题:
s.t.
(5)
为了使超球面对样本点的包裹形式更加灵活,引入核函数将样本点映射到高维空间。将式(5)中的内积(xi·xj)用核函数K(xi·xj)替代:
s.t.
(6)
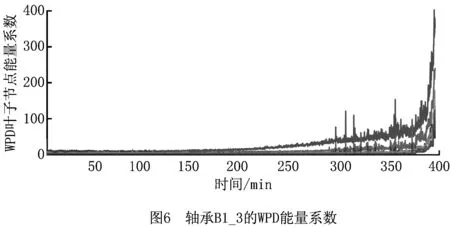
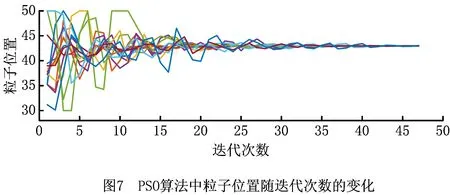
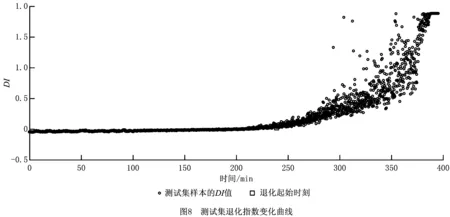
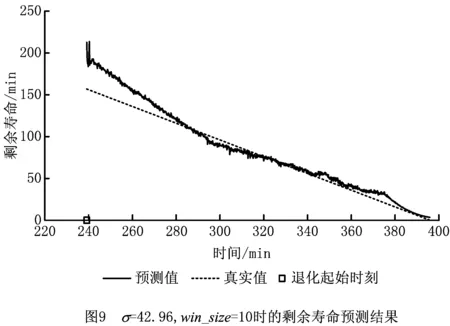
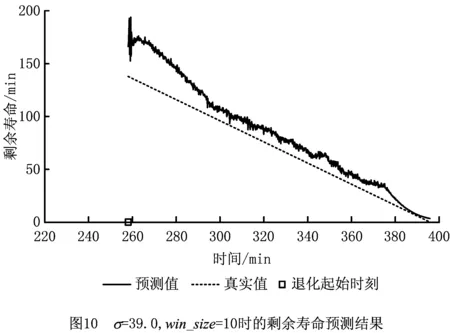
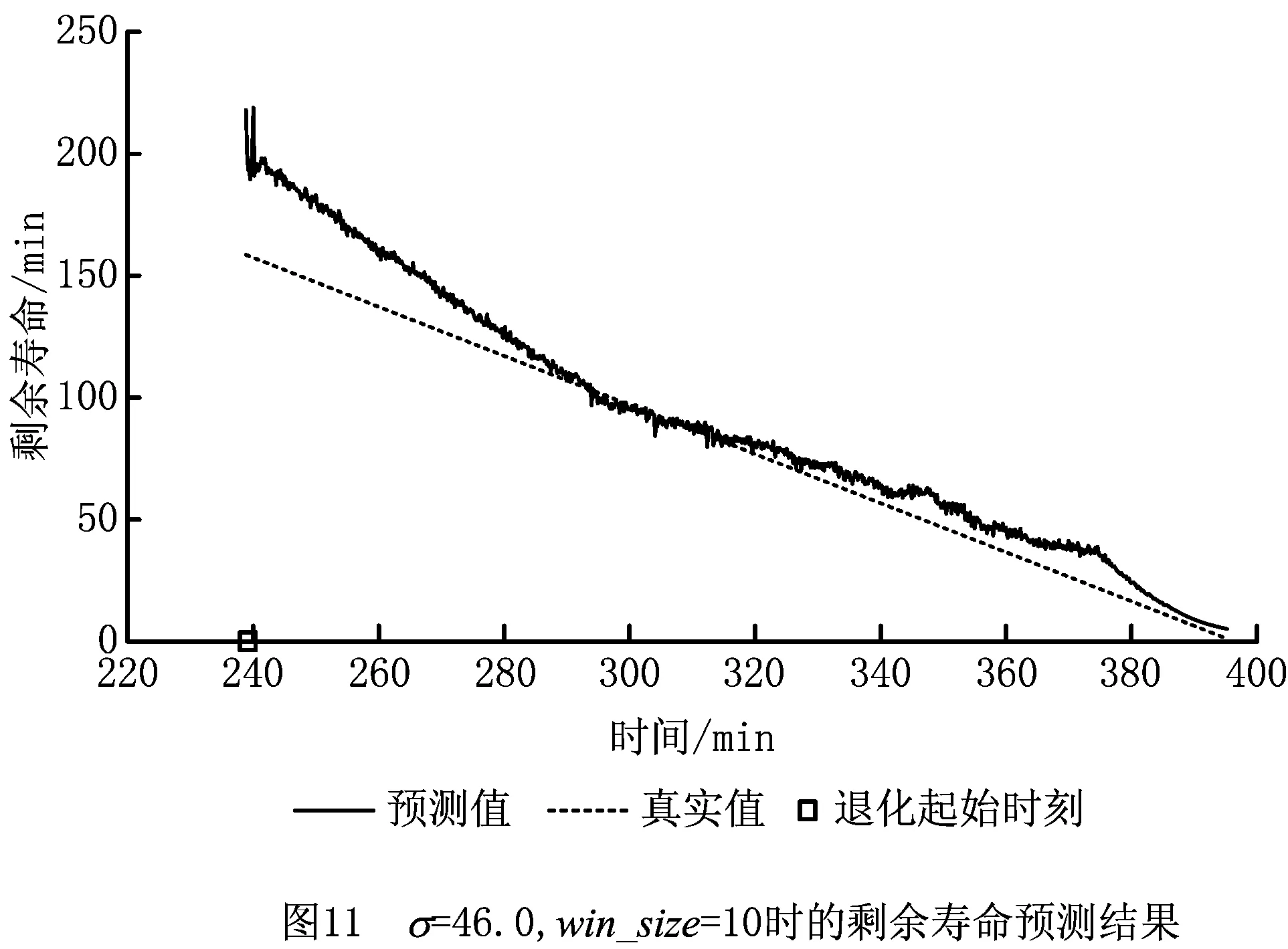
通过求解式(6)可以得到各αi的值,与0<αi 设f(z)为样本z到超球面球心距离的平方,则 f(z)=‖z-c‖2=K(z·z)- (7) 假设xsv为支持向量,由定义可知超球面半径R即为支持向量到球心的距离,化简后有 (8) 粒子群优化(Particle Swarm Optimization, PSO)算法是Kennedy和Eherhart于1995年提出的一种智能优化算法[16]。与遗传算法等进化算法类似,PSO算法首先初始化为一群随机粒子,每个粒子对应一个可行解,然后通过不断迭代找到优化问题的最优解。在每次迭代中,粒子通过跟踪个体极值和全局极值更新自己在搜索空间中的位置和速度。 设在一个D维空间中有一个规模为m的粒子群,第i个粒子的位置为xi=(xi1,xi2,…,xiD)T,速度为vi=(vi1,vi2,…,viD)T。每个粒子的适应度值由适应度函数给出,由此可以确定粒子的个体极值pi=(pi1,pi2,…,piD)T和种群的全局极值pg=(pg1,pg2,…,pgD)T。在每次迭代中,粒子在个体极值和全局极值的影响下不断优化自己的位置,并以此影响其他粒子,使整个种群朝搜索空间中最优解的方向前进。粒子的速度和位置分别按式(9)和式(10)更新: (9) (10) 式中:加速度因子c1和c2为非负常数,r1和r2为服从[0,1]均匀分布的随机数,k为迭代次数,ω为惯性权重。惯性权重决定了粒子在第k次迭代时的速度对第k+1次迭代时的速度的影响程度,具有平衡算法的全局搜索能力和局部搜索能力的作用。Shi和Eberhart于1998年提出了线性减少惯性权重的自适应策略[17],即 (11) 线性减少惯性权重可以使PSO算法在收敛的同时,具有更强的跳出局部极值的能力。式中:ωmax和ωmin分别表示权重系数的最大值和最小值,kmax为最大迭代次数。 为了加快算法收敛速度,本文对粒子位置进行了限制。设粒子位置的最大值和最小值分别为xdmax和xdmin,则在位置更新后需要对其进行如下修正: (12) 图1所示为基于PSO-SVDD的剩余寿命预测流程,包括两个阶段: (1)离线阶段 首先通过小波包分解对历史振动数据进行特征提取,然后利用PSO算法选择合适的核函数参数,针对设备健康状态的特征向量训练SVDD模型,得到超球面的半径和中心。 (2)在线阶段 从实时传感器信号提取到特征向量后,利用从离线阶段得到的SVDD超球面信息求出待测设备的退化指数,根据退化的取值判断目标部件的健康状态,并在其进入非健康状态后预测剩余寿命。 小波包分解(Wavelet Packet Decomposition, WPD)是一种通过多次迭代的小波变换对输入信号的细节部分逐步展开分析的方法,其迭代过程用一棵树表示:根节点为原始信号,根节点的下一层是对原始数据集做了一次小波变换后的结果,之后的各层均由对上一次小波变换得到的低通和高通结果递归进行小波变换求得,分解过程完成后便可计算末层不同波带的能量系数。通过迭代分解,WPD不但能够将待分析信号的频域进行逐级划分,而且能够以不同信号的特点为依据选择与其信号频谱匹配的频带,从而同时提高频域和时域的分辨率。与离散小波变换相比,应用小波包分解进行信号分析能够得到更多细节信息,得到的频域特征也更易于进行后续选择和分类。 因为小波包分解具有足够的高频分辨率,而设备部件振动信号中的故障信息大多包含于该频段[18],所以本文采用WPD进行特征提取。假设分解层数为l,则最后一层的节点数为L=2l。令fit表示最后一层第i个节点的能量,则t时刻的特征向量可以表示为 ft=(f1t,f2t,…fLt)T。 (13) 为了提高系统的鲁棒性,应对WPD结果进行Z-score标准化处理,再将标准化后的结果作为特征进行后续处理与分析。 设备部件在其使用阶段会经历由健康到失效的转变过程。健康状态的特征总是相似的,而随着退化的产生及发展,与健康状态的特征相比,新的特征在特征空间中的差异越来越显著,分布也越来越分散。 第1章已经说明,SVDD模型的建立准则为找到在特征空间包含所有样本点的半径最小的超球面。因此,如果用设备部件健康状态的历史数据训练得到SVDD超球体,则待测样本点与超球体球心间的距离可作为反映目标部件健康状态及退化发展程度的指标。 以SVDD作为健康状态评估和剩余寿命预测的基本模型,首先需要确定核函数类型及参数。与多项式核函数相比,本文采用高斯核函数,不但能够实现非线性映射,而且参数数量较少,能够有效降低模型的复杂度。高斯核函数的表达式为 (14) 由于高斯核函数的参数σ对SVDD描述样本数据的准确性影响很大,且对于不同的样本集,很难预先确定合适的σ取值。为此,本文提出一种利用PSO选择合适的核函数参数并由此训练SVDD超球面的方法。 定义退化指数 (15) DI表征退化程度的大小,DI越大,目标部件退化越严重。 假设目标部件于t1时刻进入非健康状态,于t2时刻完全故障停机。因为设备部件进入非健康状态后的故障特征随时间呈指数增长[19-20],所以由更优核函数参数计算所得的DI值随时间的变化应该更加接近指数函数。基于以上分析,本文利用DI(t1)和DI(t2)构造指数函数g(t)=aeb(t-t1),进而定义适应度函数 (16) 核函数参数的PSO算法流程如图2所示。 得到PSO算法优化的核函数参数后,利用SMO算法即可通过历史数据的特征训练SVDD超球面[15]。对于每个训练集,计算包含设备部件全生命周期的DI取值,由DI的变化情况求得该训练集进入非健康状态的时间t1和完全故障停机的时间t2,进而通过DI(t1)和DI(t2)求出表征该训练集退化过程的指数函数,为在线阶段预测剩余寿命提供依据。 在在线阶段,设t时刻由传感器监测数据经特征提取后得到的特征向量为z,则可由式(17)求得此时该设备部件的退化指数DI(t)。DI的取值越大,设备部件的退化越严重,剩余寿命越短。 一种退化检测是直接将DI的零点作为设备退化的起始时刻,当DI≤0时,则说明目标部件处于健康状态;反之,若DI>0,则说明目标部件进入非健康状态。由于实际测量所得振动信号存在噪声,可选择μ+3σ作为退化阈值,当检测窗口中DI的均值达到该阈值时,定义当前时刻为退化起始时刻,并从此时刻开始预测剩余寿命。 图3所示为剩余寿命的预测方法,其中指数曲线由训练集的DI(t1)和DI(t2)求得。 由于被测部件在进入非健康状态后,其特征向量的变化幅度很大,为了消除噪声和不稳定因素对预测精度的影响,最终输出的剩余寿命预测值由该时刻和此前(win_size-1)个时刻的剩余寿命的初始预测值经移动平均求得,以达到抑制预测值的大幅波动、更好地反映剩余寿命真实值及其变化趋势的目的。其中,win_size为移动窗口大小。 本章的实验数据来自FEMTO-ST研究院搭建的PRONOSTIA平台。PRONOSTIA是一个为轴承故障检测、故障诊断及故障预测研究服务的实验平台,能够提供球轴承从投入使用至失效的全部测量数据,平台情况如图4所示[21]。PRONOSTIA平台主要由旋转部分、负载部分和测量部分3部分构成。旋转部分通过电动机、变速系统和联轴器等带动轴承支撑轴旋转,进而使内圈与轴承支撑轴固定的轴承产生旋转运动。负载部分向测试轴承施加径向压力,加速轴承寿命周期。测量部分通过铂热电阻测量轴承工作温度,通过微加速度计测量轴承在水平方向和垂直方向的振动信号。 本文以数据集[22]中轴承B1_1和B1_3的水平方向振动信号作为训练数据和测试数据,对提出的剩余寿命预测方法进行验证。其中,采样频率为25.6 kHz,采样间隔为10 s,转速为1 800 rpm,负载为4 000 N[21]。实验首先通过WPD从训练数据和测试数据中提取特征。将小波包基设为db4,分解层数设为3,得到WPD分解树末层8个节点的能量系数如图5和图6所示。 图中不同曲线表示不同节点的能量系数随时间的变化情况。可以看出,实验初期各节点的能量系数很小,且能够在较长时间内保持平稳,说明轴承处于健康状态的时间在其整个生命周期内所占比例很大。随着时间的推移,能量系数开始增长并发生显著变化,说明轴承进入非健康状态,且故障程度逐步加深。因此,WPD树末层节点的能量系数能够反映轴承故障的演变情况,是一种有效的特征提取方法。 在利用PSO算法优化SVDD核函数参数σ时,取搜索空间维度D=1,其他参数,即种群大小m,最大迭代次数kmax,加速度因子c1和c2,权重系数最大值ωmax和最小值ωmin,粒子位置区间xmax和xmin,停止条件阈值threshold的具体设定如表1所示,得到如图7所示的优化结果。 表1 PSO参数取值 图7说明限制粒子活动范围后,PSO算法在迭代不到50次后即停止搜索,得到全局最优解p=42.96。实验还发现,当不限制粒子位置时,PSO算法在迭代70余次后满足终止条件,停止搜索,可见限制粒子活动范围能够有效减小迭代次数,加快算法收敛速度。 图3和图8所示分别为训练轴承和测试轴承的退化指数DI随时间的变化情况。实验初期DI的取值与波动幅度很小,说明轴承处于健康状态,且健康状态的时长在其整个生命周期中占有很大比例;进入退化期后,轴承的退化指数取值开始逐渐增大且产生较大波动,总体呈现出类指数函数的增长趋势,说明被测轴承的故障特征在加速发展,与轴承投入使用后的客观规律一致。因此,本文定义DI的取值能够准确反映轴承健康状态的变化情况,DI的取值越大,轴承的故障程度越深。 RMSE= (17) 表2 剩余寿命预测结果对比 σ39.0042.9646.00RMSE18.635 512.449 414.913 8 图9~图11和表2表明,本文所提方法能够有效评估轴承的健康状态并预测其剩余寿命,特别是经PSO算法选择核函数参数后,轴承剩余寿命的预测准确度得到了显著提升,比较结果说明PSO算法在优化SVDD核函数的选择时具有一定的效果和优势。 需要说明的是,因为设备部件的故障数据十分有限,而文献[5-7]中提出的ANN模型通常需要更多的训练数据才能得到相对比较理想的模型,所以在训练数据不足时易于产生较大预测误差而无法实际应用。本文提出的剩余寿命预测算法算法参数较少,易于实现,且SVDD模型在训练数据偏少的情况下与神经网络模型相比更加稳定,因此具有更高的实际应用价值。另外,文献[8-12]中健康状态的识别结果是离散的,剩余寿命由离散的健康状态识别结果估计得到,因此具有一定的阶跃特性,而当训练数据与测试数据的来源部件工作总时长相差较大时,由于目标部件在每个健康状态的持续时间难以确定,会出现较大的预测误差。由图3和图8可知,本文定义的DI不但能够表征设备健康状态的变化,而且在进入退化期后具有类似指数函数的变化趋势,因此能够通过DI的变化趋势得到更加连续、更加准确的剩余寿命预测结果。 基于SVDD模型,本文定义了能够表征设备健康状态的DI,并由此提出一种剩余寿命预测方法。首先利用WPD技术,从历史传感器状态监测数据中提取包含设备部件故障信息的特征向量;其次,引入PSO算法,求得能够使训练集DI取值的变化趋势更加接近指数规律的核函数参数;然后利用由PSO算法求得的核函数参数和设备健康状态的历史数据训练SVDD模型,通过待测样本点和SVDD超球面信息计算描述待测设备退化程度的DI;最后,通过DI随时间的变化检测退化起始时刻,利用退化期故障特征与时间的近似指数关系预测剩余寿命。 本文通过轴承加速寿命实验数据对所提方法进行了验证,实验结果表明,该方法能够有效预测轴承剩余寿命,而且利用PSO算法能够避免人为选择SVDD核函数参数时的盲目性,使得DI取值随时间的变化能够更好地描述目标部件退化过程,从而有效提升预测准确率。1.2 粒子群优化算法原理
2 基于支持向量数据描述的剩余寿命预测方法
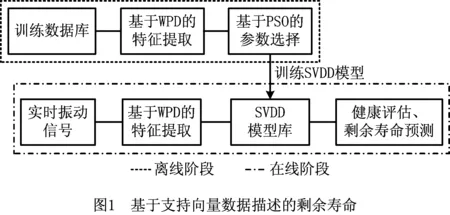
2.1 特征提取
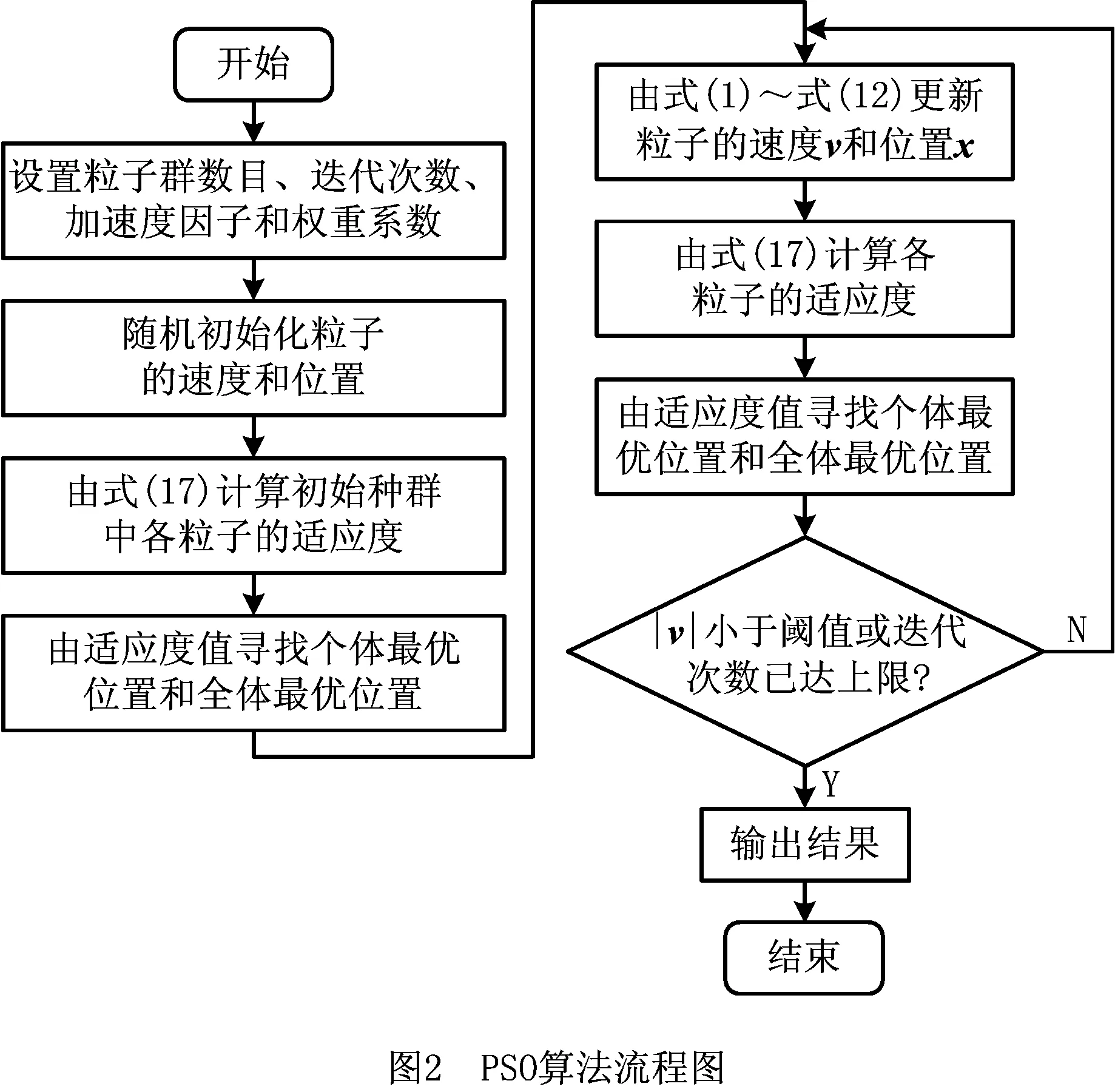
2.2 PSO-SVDD模型
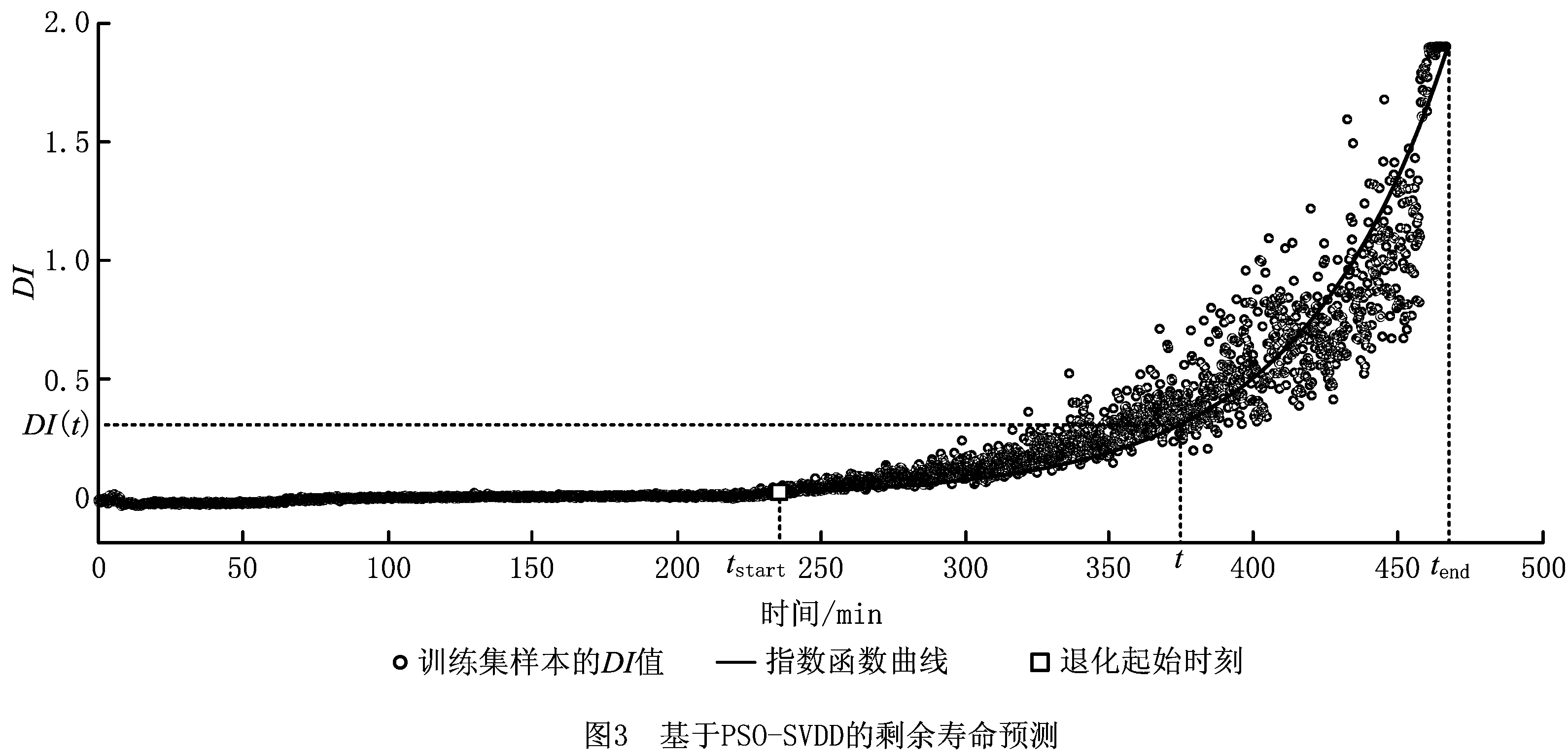
2.3 退化检测和剩余寿命预测
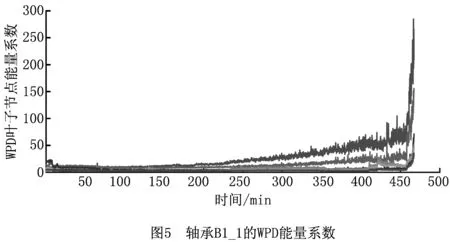
3 实验案例分析



4 结束语
