基于改进粒子群算法的多工位装配序列规划
2018-12-19刘江伟查珊珊王发麟章诗晨
刘江伟,郭 宇,查珊珊,王发麟,章诗晨
(南京航空航天大学 机电学院,江苏 南京 210016)
0 引言
装配序列规划(Assembly Sequence Planning, ASP)是以装配模型为基础,确定产品各个零部件的合理装配顺序。产品的装配是产品制造过程中的关键环节,装配序列的优劣对装配的质量有重要影响。据统计分析,产品的装配过程约占整个生产时间的50%,占制造成本的20%以上[1]。因此,产品ASP对企业缩短生产周期、降低生产成本具有重要意义。
近年来,海内外学者对ASP问题展开了大量研究,并取得了很大的进展。在装配模型构建方面,lin等[2]通过零件间的连接图、方向匹配图和空间约束图来构建零件的装配优先图,表达了零件装配的优先约束关系;章小红等[3]将产品拆卸混合图模型应用于零件间连接关系与优先关系的描述;周晓明等[4]为了得到装配体的所有几何可行装配序列,采用Petri网建立装配模型;孙占磊等[5]针对飞机曲面外形的特点,构建非正交干涉矩阵来描述各零件的几何关系;刘亚杰等[6]采用自动推理和人工输入相结合的方法,快速获得了建模所需的信息。在ASP方法方面,传统获得产品装配序列的方法主要有割集法[7]、知识推理法[8]、几何推理法[9]等,这些方法在求解简单产品时取得了很好的效果,但随着产品零件数目的增加,常会出现组合爆炸问题[10]。为了解决包含零件数目较多的复杂产品的ASP问题,近20年来,人们开始将智能算法如遗传算法(Genetic Algorithm, GA)[11]、蚁群算法[12]、粒子群优化(Particle Swarm Optimization, PSO)算法[13]、萤火虫算法[14]、和声搜索算法[15]等应用到ASP中,较好地解决了组合爆炸问题。
目前,大多数研究以产品零部件间的装配优先关系和几何关系为约束,主要集中在单工位的产品装配规划,在多工位ASP方面的研究不多。随着市场竞争压力的不断加剧,传统单工位集中式装配模式已经不能满足企业对提高生产效率、降低生产成本的要求,为了缩短产品装配周期,提高企业的竞争力,大多数企业采用多工位的串行装配线对产品进行装配。多工位串行装配线有以下3个特点:①零件在工位上的装配具有串行性;②工位对各零件的装配能力具有选择性,即装配线上的某个工位对一些零部件不具备装配能力;③各工位在装配操作总时间上具有均衡性。而以往单工位装配规划没有考虑工位装配能力对ASP的影响,也没有考虑零部件装配任务的分配对工位间装配时间平衡性的影响,因此传统单工位装配规划方法对求解多工位ASP具有一定局限性,容易出现不满足工位要求的伪优解。在多工位ASP方面,王丰产等[16]首次提出多工位ASP的PSO算法,在对序列规划的同时对装配任务也进行了分配;袁文兵等[17]采用多子种群并行搜索模式,提出基于果蝇优化算法的多工位ASP方法,实现了对多工位多成本装配序列的进一步优化。以上方法对多工位ASP提出了新的思路,取得了很好的效果,但这些方法针对的是无序工位的序列规划,其对多工位串行装配线的ASP仍具有一定局限性。
因此,本文结合多工位串行装配线的特点,将工位装配能力和工位装配时间均衡性这两个工位因素引入ASP过程中,提出基于改进粒子群优化(Improved Particle Swarm Optimization, IPSO)算法的多工位序列规划方法。首先,通过构建装配干涉矩阵、工位能力矩阵、装配工具表和装配操作时间表,描述了产品各零部件间的几何关系及零部件与工位之间的关系;同时建立了以装配序列可行性、装配方向一致性、装配聚合性和工位间平衡性4个因素为评价指标的适应度函数,并给出了各评价指标的求解方法。然后,将离散化的粒子群算法应用于零部件装配序列模型的求解及装配任务的多工位分配。针对粒子群算法容易陷入局部最优的问题,对惯性权重进行了改进,并提出了粒子相似度和相似度阈值的概念;通过相似度阈值控制粒子的变异,提高了算法的全局搜索能力。最后,本文以包含16个零部件的某型发动机为对象,利用IPSO算法获得了该装配实例的最优装配序列和零部件的多工位分配结果,并将该算法与GA和一般粒子群优化(General Particle Swarm Optimization, GPSO)算法进行了比较。
1 多工位装配模型
产品的ASP需要满足一定的约束条件,通常将这些约束条件分为完全约束和优化约束两大类。在装配过程中,如果违反了完全约束,则将产生不可行的序列;如果违反了优化约束,则将生成低效率低质量的装配序列。单工位装配序列规划往往将零件间的优先装配关系和几何关系作为完全约束,多工位装配序列规划还需要考虑工位的装配能力约束,以防止产生不满足工位要求的不可行解。在优化约束方面,单工位序列规划通常以装配稳定性、装配工具改变次数、装配方向改变次数等为目标,多工位装配规划则还需考虑装配任务分配对工位间平衡性的影响,以保证规划得到的装配序列满足工位间装配时间平衡性的要求。
1.1 装配序列可行性
1.1.1 几何可行性
一条可行装配序列需要保证产品各零件在装配时不发生碰撞。通常,装配干涉矩阵被用来表示装配体各零部件间的干涉关系。而在评估装配序列可行性、确定待装配零件的可行装配方向时也需要用到装配干涉矩阵。装配干涉矩阵
p1p2…pn
(1)
式中:pi表示第i个零件,n为零件数;d表示笛卡尔坐标系中x,y,z3个正方向;adij表示零件pi沿d方向装配时与零件pj的干涉情况,当发生干涉时adij=0,否则adij=1。
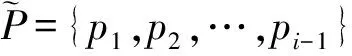
(2)
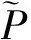
(3)
对于任意装配序列P={p1,p2,…,pn},其Npbi的求解方法为
(4)
1.1.2 工位可行性
多工位串行装配线中(如图1),后续工位在装配时需要等前续工位完成所有装配活动后才能开始本工位的装配活动。与此同时,受到工位上装配工具、夹具、人员等装配资源的限制,每个工位装配产品各零部件的能力不同,本文采用工位能力矩阵描述多工位串行装配线上各工位的装配能力。装配序列规划时需要评估每个工位的装配能力,以保证零件在具有装配能力的工位上装配,防止产生不可行序列。装配工位的工位能力矩阵
S1S2…SQ
(5)
式中:Sk表示第k个工位;Q为工位总数;cik表示工位Sk对零件pi的装配能力,当零件pi能够在工位Sk上装配时cik=1,否则cik=0。

装配序列的工位可行性用不满足工位装配能力的零件数目(Nbsc)来描述。对于任意序列P={p1,p2,…,pi,…,pn},其工位可行性
(6)
(7)
装配序列的可行性(Nfoa)是装配规划的前提条件,其在多工位装配规划中体现在几何可行性与工位可行性,因此可以用Npbi和Nbsc定量描述为
Nfoa=Npbi+Nbsc。
(8)
1.2 装配方向一致性
装配方向一致性即装配方向的改变次数(Nadc)。当零件的装配方向发生改变时,装配机械手将因换向操作而浪费装配时间,导致装配成本增加。因此,在装配过程中要降低装配方向的改变次数。对于任意装配序列P={p1,p2,…,pi,…,pn},由式(2)获得零件pi的可行装配方向集Di,该装配序列的Nadc求解步骤如下:
步骤1令i=1,Nadc=0,装配方向AD=D1。
步骤2令i=i+1,如果i>n,则转步骤5;否则,转步骤3。
步骤3AD=AD∩Di,若AD=∅,则Nadc=Nadc+1,AD=Di;否则,转步骤4。
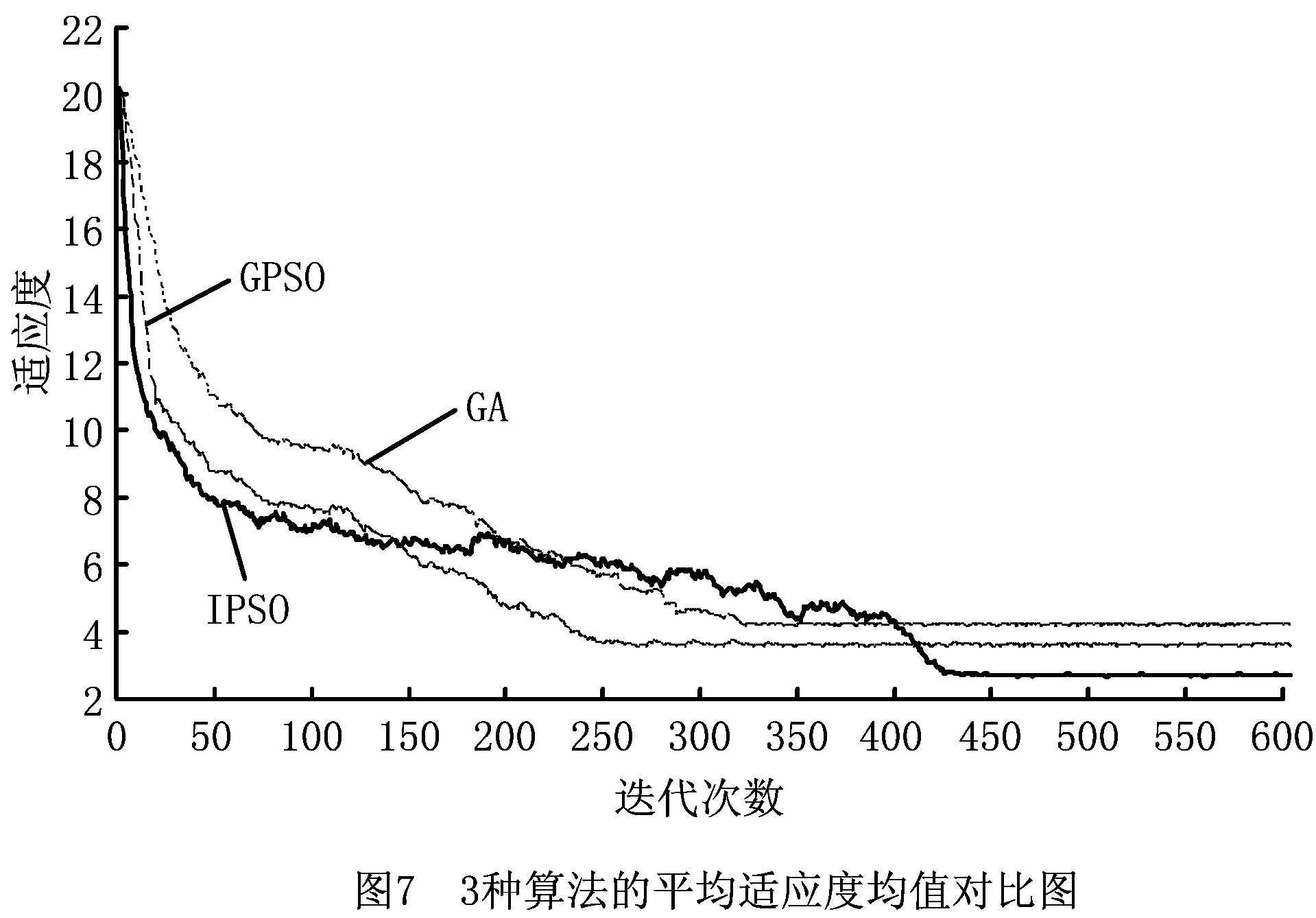
步骤4如果i 步骤5输出Nadc,结束。 装配聚合性即装配工具的变换次数(Natc)。产品在装配过程中需要采用不同的辅助工具,且不同待装配零件用到的工具也不尽相同,因此产品装配时会经常变更装配工具,这属于无效劳动,会增加产品装配时间,降低装配效率,应尽量减少不必要的工具更换。每个零件装配时需要用到的装配工具由零件的几何形状特征、装配操作类型和车间工具库存共同决定。定义每个零件的装配工具表为TE=(tie)n×e,对于序列P={p1,p2,…,pi,…,pn},当零件pi需要工具Te进行装配时,tie=1,否则tie=0。因此,该序列 (9) (10) 式中:TE(pi)为零件pi的装配工具向量,Tc表示装配零件pi和pi+1时更换工具。 工位的间平衡性即工位间装配时间的均衡性(Bsat),其对产品生产节拍、生产成本有重要影响。工位间生产任务分配不平衡,会导致生产周期变长,引起生产瓶颈,出现生产效率低下、生产资源利用率不均等现象。传统的单工位ASP没有将装配操作时间考虑在内,导致分配装配任务时容易使各工位装配总时间不均衡,无法满足装配线平衡的需求。本文用各工位总装配时间的标准差衡量工位间的平衡性,定义每个零件的装配操作时间表为TO(oi2)n×2,oi2表示零件pi的装配时间。序列P={p1,p2,…,pn}的工位间均衡性 (11) 步骤4若η≥n,则计算Bsat,转步骤6;否则,转步骤5。 步骤5令r=1,若k 步骤6输出Bsat,结束。 产品在优化装配序列时往往涉及众多参数,本文主要考虑与多工位装配有关的因素,将装配序列可行性、装配方向一致性、装配聚合性和工位间平衡作为评价指标,构造目标函数 f=cdNadc+ctNatc+cbBsat+cfNfoa。 (12) GPSO算法的位置与速度是实值计算,对求解ASP这种离散问题并不实用。因此,本文对GPSO算法进行离散化,重新定义粒子的位置、速度及其更新操作。 定义1粒子的位置。粒子的位置用装配体各零件编号的排列表示。第m个粒子的位置矢量表示为Pm=(pm1,pm2,…,pmi,…,pmj,pmn),其中pmi∈{1,2,…,n}为零部件编号,n为装配体中零部件的数目。对于任意零部件pmi和pmj,如果i≠j,则pmi≠pmj。 定义2粒子的速度。粒子的速度用于更新粒子的位置,种群中第m个粒子的速度矢量表示为Vm=(vm1,vm2,…,vmi,…,vmn),第m个粒子速度Vm的改变即装配序列Pm中零部件排列顺序的一种变换,其中vmi∈{0,1,2,…,n},vmi为粒子m速度矢量中的第i维元素,表示粒子m中pmi对应的速度,当vmi≠0时,零件pmi在粒子Pm中的排列位置需发生改变。 定义4位置间的减法。两个粒子位置相减产生一个新速度,若P1=(p11,p12,…,p1n),P2=(p21,p22,…,p2n),则定义P2ΘP1=V,其中V为新速度。V的取值方式如下:若p1i=p2i,则vmi=0;否则vmi=p2i。 (13) 定义6速度的加法。假设两个速度分别为V1=(v11,v12,…,v1n)与V2=(v21,v22,…,v2n),则速度的加法定义为V1⊕V2=V3,V3的确定方法如下: (14) (15) (16) 近年来,PSO算法在NP-Hard问题(如旅行商问题[18]、调度问题[19]等)得到了广泛应用。与GA、蚁群算法等相比,PSO算法具有参数少、结构简单、实数编码、搜索速度快等优点,但是也存在局部搜索能力差、搜索精度不高、容易陷入局部极小解、对参数敏感等问题[20]。因此,有必要对PSO算法进行改进,从而提高算法的搜索效率和搜索能力。 2.2.1 惯性权重的改进 PSO算法中,惯性权重因子w表示当前粒子速度对速度更新的影响,其能够调节粒子种群的全局搜索和局部搜索能力。较小的w有利于局部搜索,能够更好地搜索到最优值,较大的w能更快地搜索解空间,提高算法的收敛速度。本文对惯性权重w进行改进,使w随算法的迭代而动态改变: (17) 式中:wmin为w的最小值,wmax为w的最大值,t为当前迭代次数;Gmax为最大迭代次数,f为粒子当前的适应度值;favg,fmin和fmax分别为种群的平均、最小和最大适应度值。 在算法初始阶段,各粒子比较分散,较大的惯性权重使粒子有较大的速度,从而有较强的探索能力,使种群快速收敛于一个较好的解,提升了算法的搜索效率;在算法的后续阶段,较小的惯性权重能够帮助粒子对当前的求解区域进行精确局部搜索,提高算法的搜索精度。与此同时,为了保留目标函数值优于平均目标值的粒子,应给其分配较小的惯性权重,而对于目标函数值差于平均目标值的粒子,则设置较大的惯性权重,从而使粒子向更好的目标区域靠近。 2.2.2 相似度和相似度阈值 为了保证算法迭代过程中种群具有较好的多样性,本文采用粒子相似度衡量某个粒子与种群中其他粒子的相似程度,并通过动态地设置种群的相似度阈值来控制粒子变异,防止种群过早地陷入局部最优。假设粒子种群容量为M,每个粒子代表n个零部件的装配序列,则粒子Pm的相似度 (18) (pmi (19) (20) 式中:St为相似度阈值,Stmin为相似度阈值最小值,n为零件个数,t为当前迭代次数,Gmax为最大迭代次数。 当Sm比较小时,粒子之间的差异比较大,粒子种群的多样性较好;反之,粒子间的相似程度高,粒子种群可能陷入局部最优解。而且,随着算法的迭代,粒子的相似度是一个逐渐递增的过程。因此,需要动态地设置相似度阈值St,使得算法前期种群具有丰富的多样性,算法后期种群能尽快收敛。St设置方式见式(20)。 当粒子Pm的相似度Sm大于相似度阈值St时,对该粒子进行变异,具体的变异操作定义为交换粒子 Pm中的任意两个零件,变异操作的次数为NV, NV=⌈Sm-St⌉。 (21) 式中⌈⌉为向上取整符。将变异后的粒子作为种群的新个体进行适应度计算,从而扩大搜索空间,跳出局部最优解。 在分析多工位串行装配线与PSO算法特点的基础上,采用IPSO算法求解多工位装配模型。首先通过多工位装配模型获得装配体各零部件间的装配干涉情况、各工位的装配能力、各零部件所使用的工具信息,以及装配操作所需要的装配时间,构建考虑几何约束和工艺约束的适应度函数,然后以此适应度函数为目标,通过算法的不断迭代获得同时满足几何约束和工位约束的最优多工位装配序列和装配任务分配结果。具体流程如图2所示。 在传统生产过程中,某型号发动机为单工位固定式装配,随着市场上该发动机需求量的增加,企业为了降低生产周期、提高装配效率、增加产量,将该发动机的装配方式改为多工位串行装配生产线。因此,本文以该发动机为对象,将IPSO算法应用于多工位ASP的可行性验证。发动机爆炸图如图3所示。 通过分析发动机的三维模型和装配工艺信息,得到各零部件的装配工具使用情况如表1所示,装配操作时间信息如表2所示;发动机零部件间的干涉矩阵AM和各工位的工位能力矩阵CM分别为: p1p2p3p4p5p6p7p8p9p10p11p12p13p14p15p16 S1S2S3S4S5 表1 零部件装配工具表TE 续表1 表2 零部件装配时间表TO 续表2 应用以上装配信息,在MATLAB R2014a中编写了相应的IPSO算法程序,具体实验环境为:Intel酷睿I5 2450 M,CPU主频2.5 GHz,内存4 GB,Windows 7 64位操作系统。经过多次对比测试发现,当Gmax=600,wmin=0.35,wmax=0.75,c1=1.5,c2=0.9时,算法的寻优能力和收敛性接近最佳状态。针对该发动机装配,工位数Q=5,最小相似度阈值Stmin=4,结合实际装配生产线中对各评价指标重要性的分析和评估,设置适应度函数中的各权重系数cd=0.3,ct=0.3,cb=0.4,cf=2。保持IPSO算法参数和适应度函数中各权重系数不变,重复运行50次,当种群容量为20,40,80,150时,得到的最优装配序列和工位分配结果如表3所示。根据该表得到的最优序列和和各工位装配任务,在DELMIA V6中建立发动机在工位上的装配流程,如图4所示。 从表3的实验结果可以看出,不同种群容量下得到的最优装配序列均满足工位的装配能力,因此本文将IPSO算法应用于多工位的ASP是可行的。同时,不同种群容量对全局最优解的求解有一定影响,虽然本文对GPSO算法进行了改进,并用粒子的相似度控制了粒子变异,但是因为约束条件过多,较小的种群容量仍然难以得到全局最优解,而种群容量为150时得到的最优适应度仍为2.665 7,所以2.665 7为全局最优适应度值。 图5所示为种群容量取80、实验次数为50时,各代平均适应度均值和最优适应度均值的变化趋势。图6所示为50次实验中其中一次的各代最佳和平均适应度变化情况。 表3 不同种群规模下得到的最优装配序列和工位分配结果 续表3 由图5可知,在算法迭代初期,种群的平均适应度均值和最优适应度均值都比较大,尤其是种群在第一代时的平均适应度均值达到20.059 2,可见实验过程中初始生成的装配序列可行性较差,存在较多不满足几何约束或工位装配能力的装配序列。而在算法不断迭代过程中,平均适应度均值和最优适应度均值都呈下降的趋势,并且最终都收敛于最优或近似最优值。由此可见,算法对初始装配序列的可行性要求不高,且算法的收敛性好。在图6中,平均适应度值在算法迭代的前中期出现了多次跳跃变化,这是由于相似度控制使粒子产生了变异,形成了新的粒子,丰富了种群的多样性,使得种群在陷入局部最优解时能够及时跳出;而相似度阈值的动态设置使种群在算法迭代后期能够尽快收敛。同时,平均适应度和最优适应度稳步下降说明用粒子相似度控制粒子变异的方法不会影响算法的收敛趋势。 为了进一步检验IPSO算法解决多工位ASP问题的可行性和优越性,本文将IPSO算法与GPSO算法和GA算法进行比较。保持装配对象、目标函数、算法参数和运行环境不变,GPSO算法的惯性权重为0.65。针对该装配实例,多次实验对比发现,当交叉概率为0.85,变异概率为0.09时,GA的寻优能力接近最佳。种群容量分别取40,80,150,50次实验结果的对比如表4所示。当种群容量为80时,3种算法的平均适应度均值变化对比如图7所示。 表4 3种算法的实验结果对比 续表4 从表4可以看出,不管种群容量是40,80还是150,IPSO和GPSO算法得到的可行装配序列比GA得到的都要多。当种群容量为40时,GA只得到16条可行装配序列,说明GA对种群的初始质量要求比较高。在相同种群规模下,IPSO算法求得的最优适应度值比GPSO和GA都好,说明本文的IPSO算法具有更强的寻优能力。在运行时间上,IPSO算法的单次运行时间多于GPSO和GA,且种群容量越大,运行时间的差异越明显,这是由于种群的每一次迭代过程中都要计算每个粒子的相似度,当相似度超过阈值时还要进行相应的变异操作,增加了算法的求解时间。但在种群容量为150、迭代次数为600时,IPSO算法的单次运行时间也只有130s左右,在可接受范围之内。从图7可以看出,在算法迭代的前期,IPSO算法的收敛速度比GPSO算法和GA更快;在算法的中、后期,由于相似度的加入和相似度阈值的控制,虽然降低了收敛的速度,但使种群能够跳出局部最优解,加大了种群收敛到全局最优解的概率。 本文针对传统单工位固定资源规划得到的装配序列容易出现不满足串行装配线工位装配能力和工位间平衡性的问题,将工位约束纳入ASP过程中,提出了基于IPSO算法的多工位ASP方法。以装配体几何约束、工位约束和优化约束为条件,建立了多工位装配模型,构建了以装配序列可行性、装配方向改变次数、工具改变次数和装配操作时间为评估因素的适应度函数。由于GPSO算法在求解NP-Hard问题时易陷入局部最优解,本文对算法中惯性权重的设置方式进行了改进,同时提出粒子相似度和相似度阈值的概念,并通过动态设置相似度阈值来控制粒子的变异,以提高算法的寻优能力。最后,以某型发动机为装配实例,对本文构建的装配模型及其求解算法在解决多工位ASP问题方面的可行性进行了验证。 本文在构建多工位装配模型时,将装配方向一致性、装配聚合性和工位间的平衡性作为优化约束中的优化指标,未考虑装配线上的物流配送、人员装配水平等因素,下一步工作将在现有装配模型中加入物流、人员等要素,使所建立的装配模型更加贴合实际生产需求。另外,本文在装配序列规划时只考虑了零部件的串行装配,只能生成串行的装配序列解,而并行作业的装配模式可以进一步缩短产品的装配时间、提高装配效率,因此后续将对并行ASP问题展开进一步研究。1.3 装配聚合性
1.4 工位间的平衡性
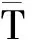
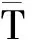

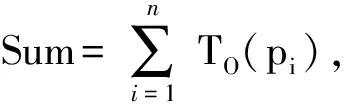
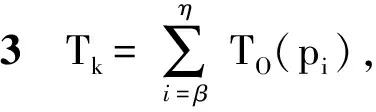
1.5 适应度

2 面向多工位装配序列规划的改进粒子群优化算法
2.1 一般粒子群优化算法的离散化
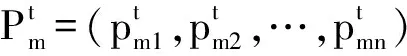
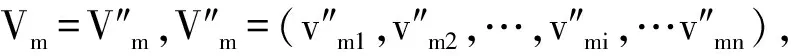
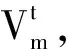
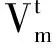
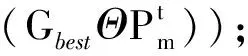
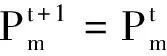
2.2 改进的粒子群优化算法
2.3 改进的粒子群优化算法流程及步骤
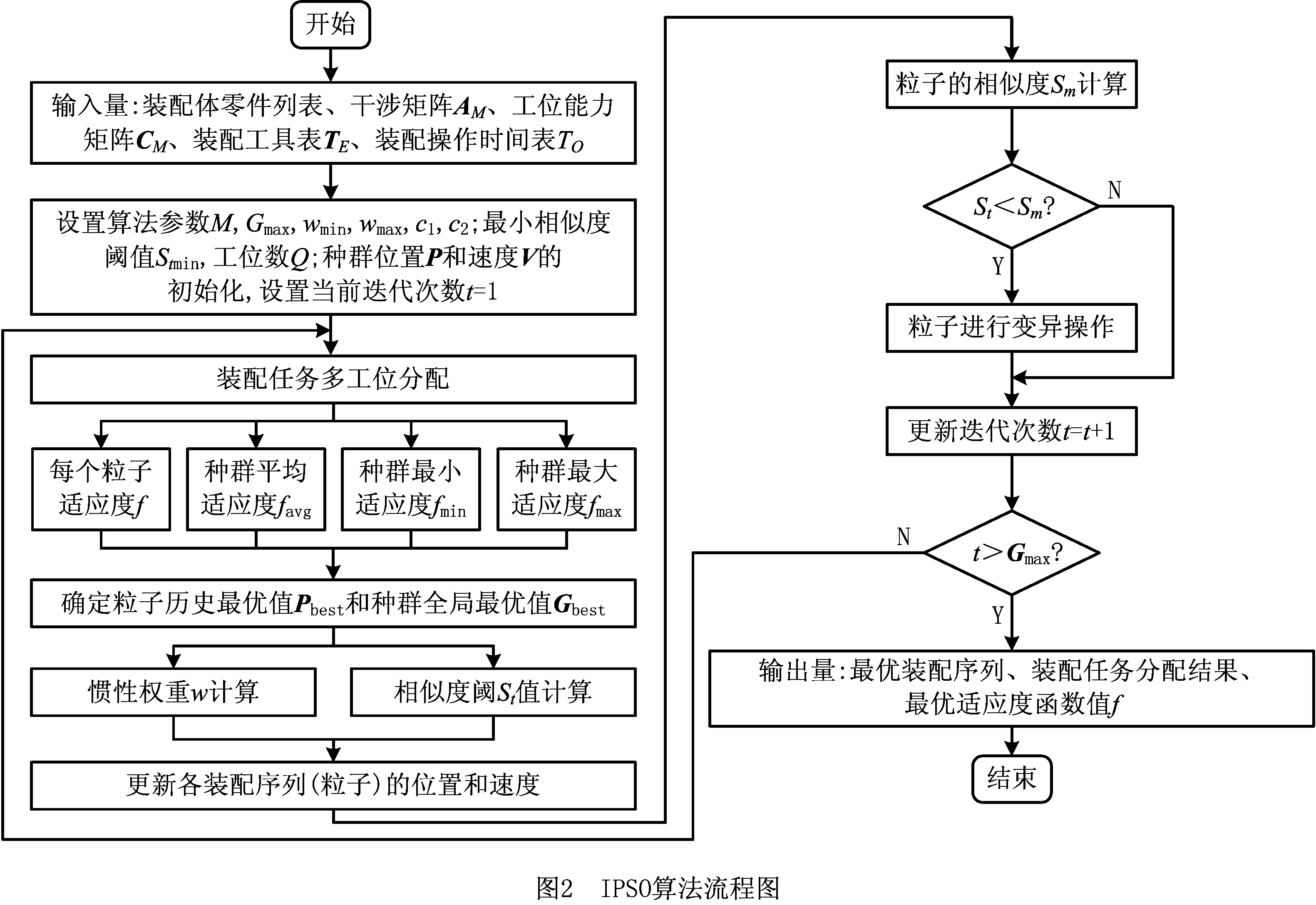
3 实例对比分析
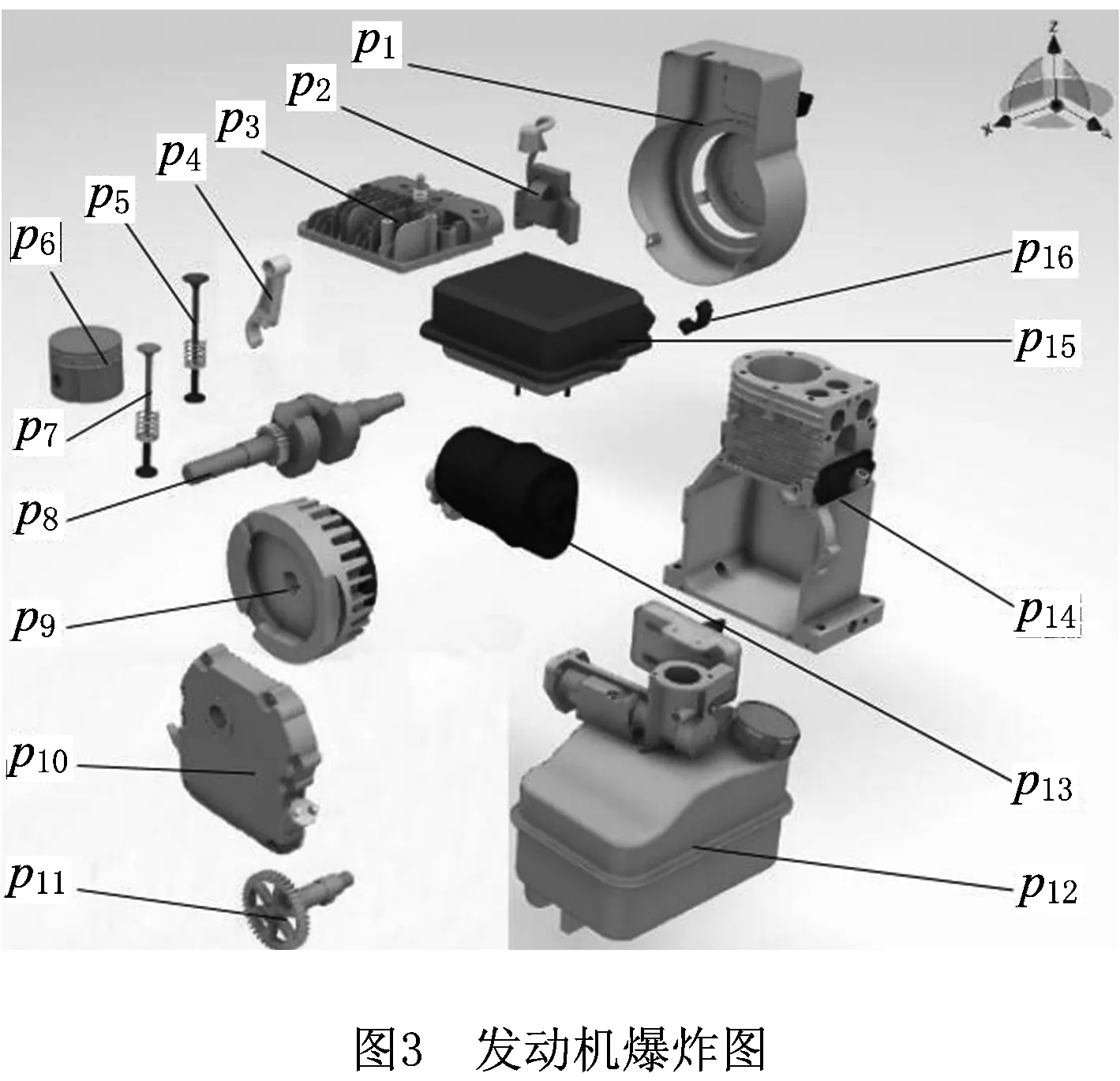
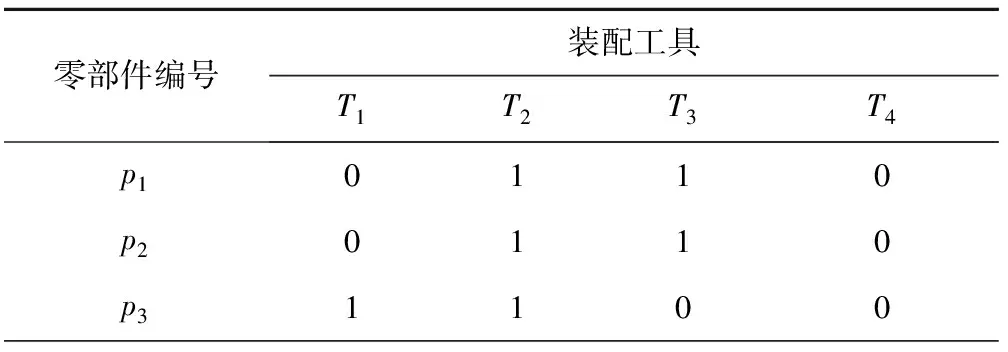
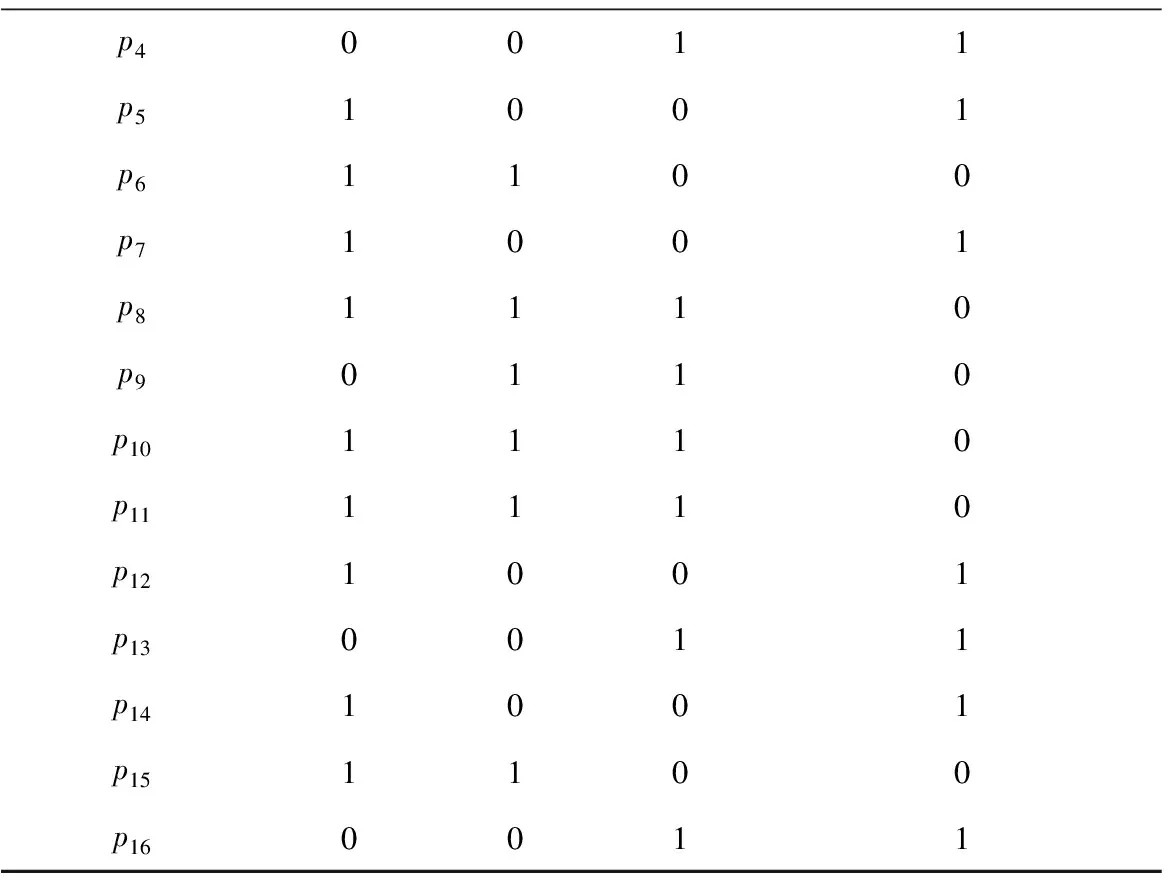
3.1 基于IPSO的多工位装配序列规划实验


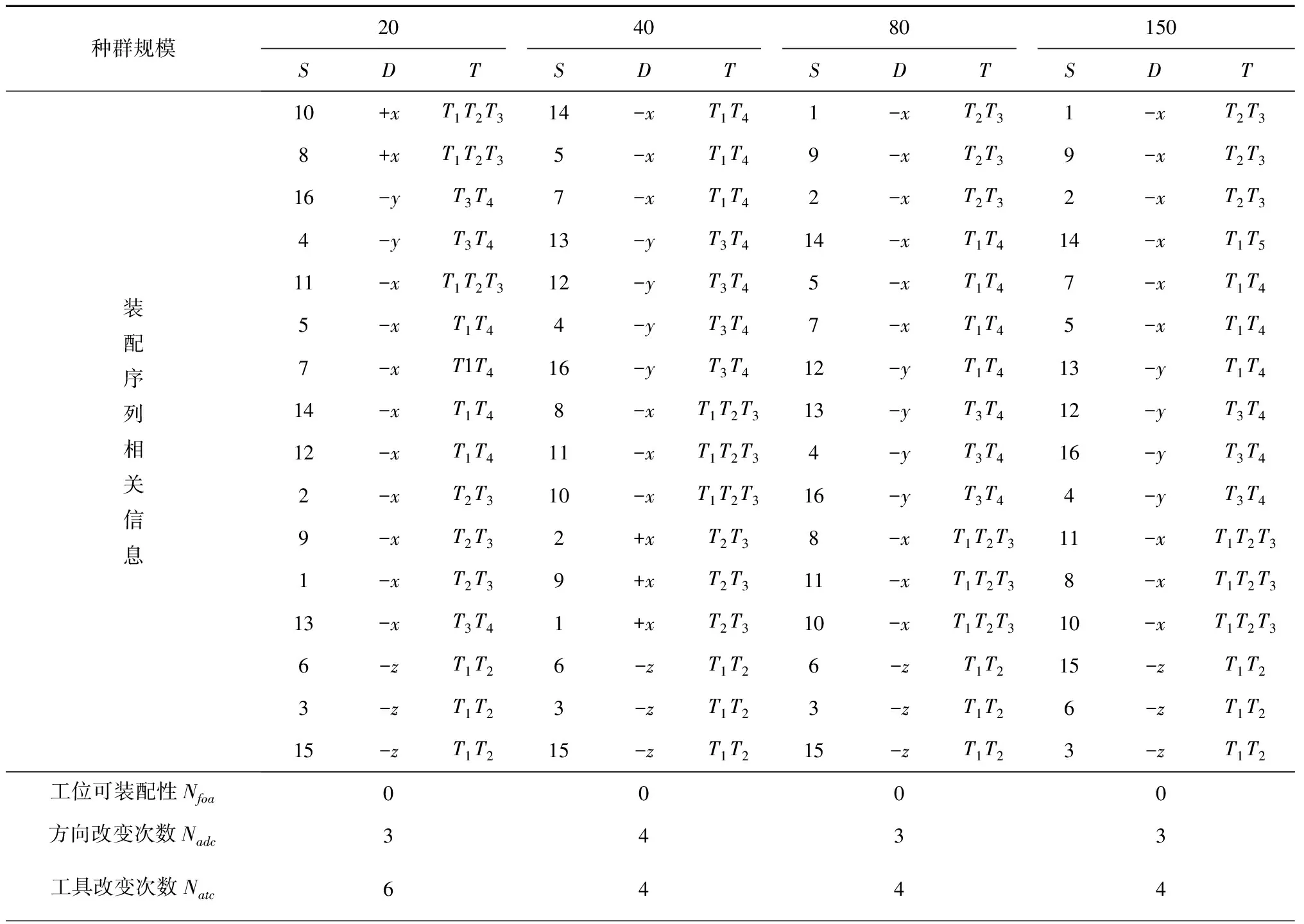
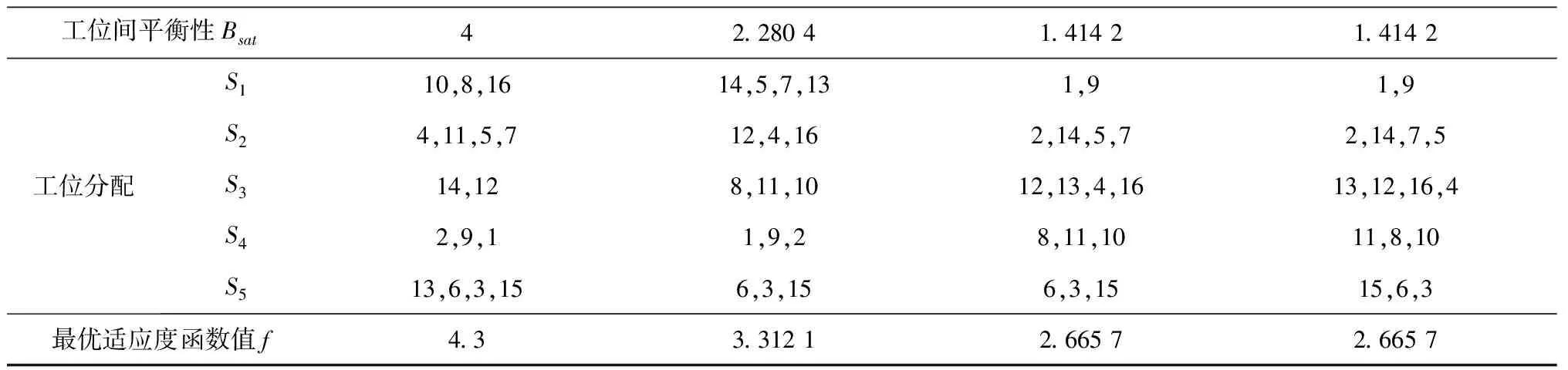

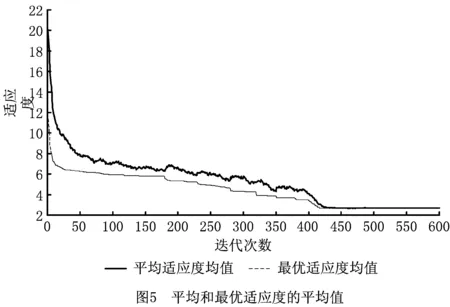
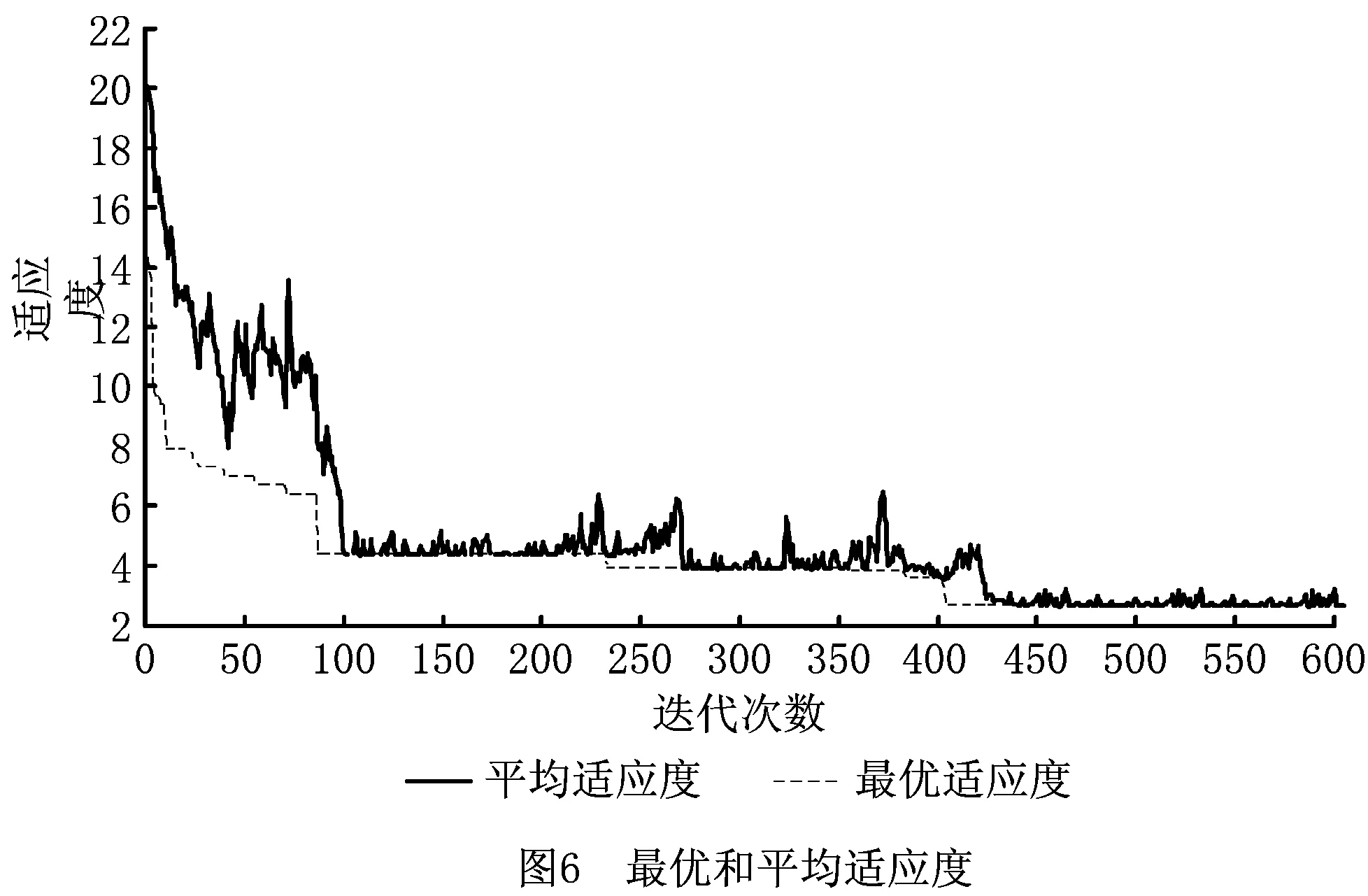
3.2 算法比较分析


4 结束语
