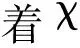坑中坑式内撑支护基坑内坑对外坑土压力影响
2018-12-18陈秋旺
陈秋旺
(福建西海岸建筑设计院 福建福州 350011)
0 引言
城市化推进过程中,地下空间扩容工程发展迅猛,城市建设越来越密集化,基坑数量亦随之增长。同时,建筑工程在多功能需求影响下,需要容纳电梯井、集水井或不同深度的裙楼基础,导致原有的基坑需要进行二级开挖,形成了“坑中坑”式基坑[1-2]。
针对坑中坑式基坑工程,若内坑开挖尺寸相对较大或外坑平台宽度相对较小时,基坑容易因围护结构变形过大而导致失稳,其整体稳定性将受到极大的挑战,因此,坑中坑开挖影响不容忽视。目前,关于坑中坑式基坑工程研究仍较少报道,相关设计与施工更多依赖岩土工程师们的经验判断,往往采取相对保守的设计方法,容易引起工程造价的提高。根据现有的设计方法,考虑坑中坑式基坑设计的两种极端情况:①偏安全设计,考虑单基坑开挖,即不区分内外坑,以内坑开挖深度为坑中坑式基坑整体开挖深度,提高支护体系刚度。②低估坑中坑开挖影响,即忽略坑中坑存在,基坑易因整体稳定性不足而破坏,安全性难以保障。
基坑围护结构的侧向变形,在宏观上是由于土压力作用而引起,也是围护结构承受的主要水平荷载,因此,计算坑中坑式基坑围护结构土压力大小与分布模式,有重要的理论意义和现实意义。研究表明,坑中坑土压力的大小与分布模式与内坑相对位置与尺寸息息相关,而经典土压力理论无法考虑内坑的影响,既有规范也无相关计算方法可供参考,因此,考虑二级基坑开挖影响的土压力大小与分布形式相关研究亟待开展。
申明亮等[3-4]考虑土压力叠加,结合库伦土压力理论,提出了可以考虑坑中坑开挖影响的外坑被动土压力解析方程。林兴利等[5]认为,内外坑坑间土存在土拱效应,基坑破坏区域由刚塑性滑裂体组成,基于平行墙土拱理论,得到了考虑土拱效应的外坑被动土压力计算方法。谢灵翔[6]认为,经典的土压力理论的建立基础是半无限土体假设,不符合坑中坑式基坑土压力计算,将极限平衡理论与平面滑裂面假设结合,考虑不同滑裂面与土体强度参数,推导了4种被动土压力计算方法。胡辉等[7]针对无黏性地基土开挖坑中坑,且外坑平台宽度较小,内坑支撑刚度较大,基于土拱理论,通过建立水平微分方程得到了外坑围护结构被动土压力计算方程。
本研究认为,数值模拟可以较为准确地反映基坑围护结构与周边土体相互作用性状。以坑中坑式内撑支护基坑为研究对象,拟采用二维有限元软件Optum G2,选择可以考虑土体硬化过程的HMC本构模型模拟地基土,分析坑中坑开挖对外坑被动土压力大小及分布模式的影响,进一步揭示坑中坑式基坑围护结构土压力分布规律。
1 工程概况
某大型公共建筑物为典型的坑中坑式内撑支护基坑工程,相应的平面示意图如图1所示。内外坑围护结构均采用沉管灌注桩。取基坑横向断面为研究对象,外坑宽度 为60m;深度 为6m,对应围护结构插入深度 为6.5m,即埋深为12.5m,离地表-2m处对外坑设置水平支撑一道;内外坑平台宽度 为18m,内坑宽度为27.7m,深度 为5.5m,对应围护结构插入深度 为5m,离地表-7m处对内坑设置水平支撑一道。
图1 某大型公共建筑物工程A区平面示意图
2 数值模拟
Optum G2是一款结合极限分析与有限元的二维平面数值软件,具备网格自适应功能,能够细化覆盖在剪切带附近的网格,有效避免局部土体破坏,在网格数量较少的情况下,亦能较为精确地搜索得到明显的剪切滑移带,大幅度提高计算精度,并节约计算时间。
数值模型采用标准边界条件,即假设模型两侧无水平位移,底部固定约束,顶部则为自由边界,如图3所示。土体本构选用可以反映基坑开挖卸荷特性的硬化摩尔库伦模型(Hardening Mohr Coulomb,简称HMC模型)。因基坑开挖前已完成降水疏干,且施工周期长,故选择有效应力指标,土体设置为排水状态。墙-土界面相互作用性状可利用摩尔-库伦屈服准则进行描述,其强度参数τi可表示为式(1):
τi=τf×Rinter
(1)
其中,τf为排水条件下围护墙周边土体抗剪强度,Rinter为界面强度折减因子。
采用分步开挖进行模拟坑中坑式内撑支护基坑施工过程,具体如下:
①初始地应力计算(K0法);②同时激活内、外坑围护结构;③外坑开挖至地表下-2.5m(GL -2.5m,第一层);④离地表-2m处对外坑设置一道水平支撑;⑤外坑开挖至GL -6m,对应外坑坑底;⑥开挖内坑至GL -7.5m(内坑第一层);⑦离地表-7m处对内坑设置一道水平支撑;⑧内坑开挖至GL -11.5m,对应内坑坑底。
3 算参数选取
基于地质勘察报告,将各土层进行等厚处理,对相近土层进行归并简化,总结各土层厚度分布以及物理力学参数如表1所示。
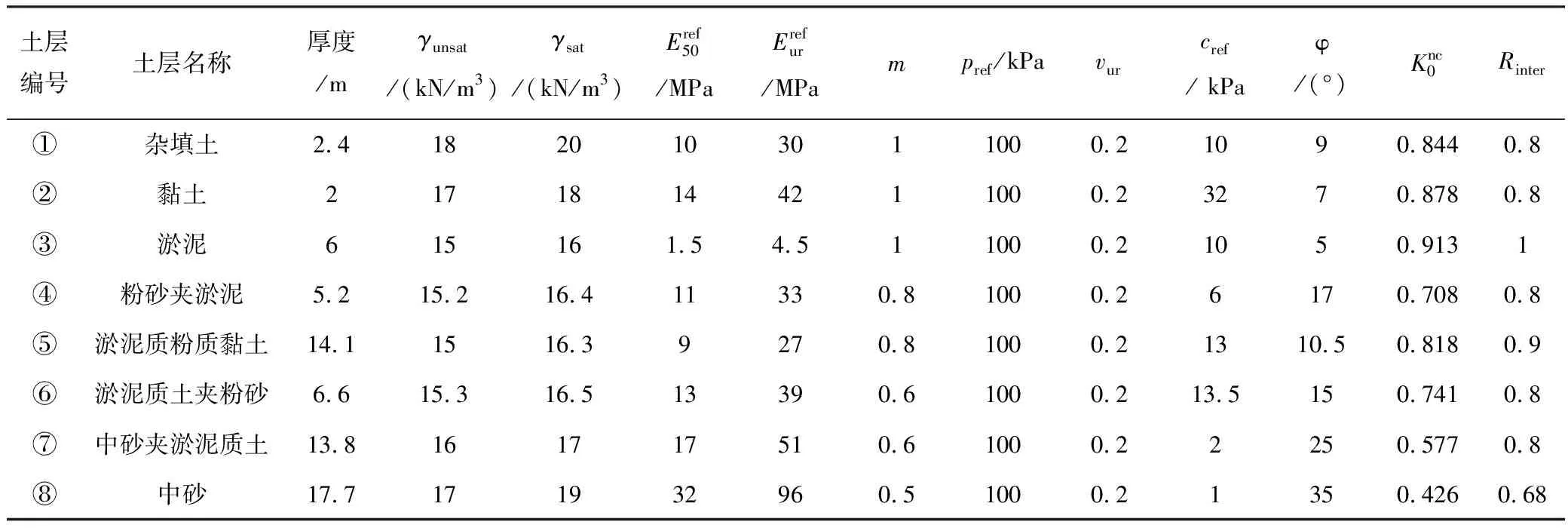
表1 土层厚度及物理力学参数
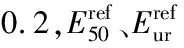
沉孔灌注桩桩径为0.6m,间隔1m,其结构示意图如图2所示。为便于数值建模与分析,采用等效刚度法将沉管灌注桩转换为地下连续墙,可得到基坑围护结构及水平支撑力学参数如表2所示,计算公式[8]如式(2):
(2)
其中,b为相邻桩中心距,h等效连续墙厚度,d为灌注桩桩径。
结合几何模型(图3)与计算参数(表1~表2)建立了相应的数值模型,如图4所示。
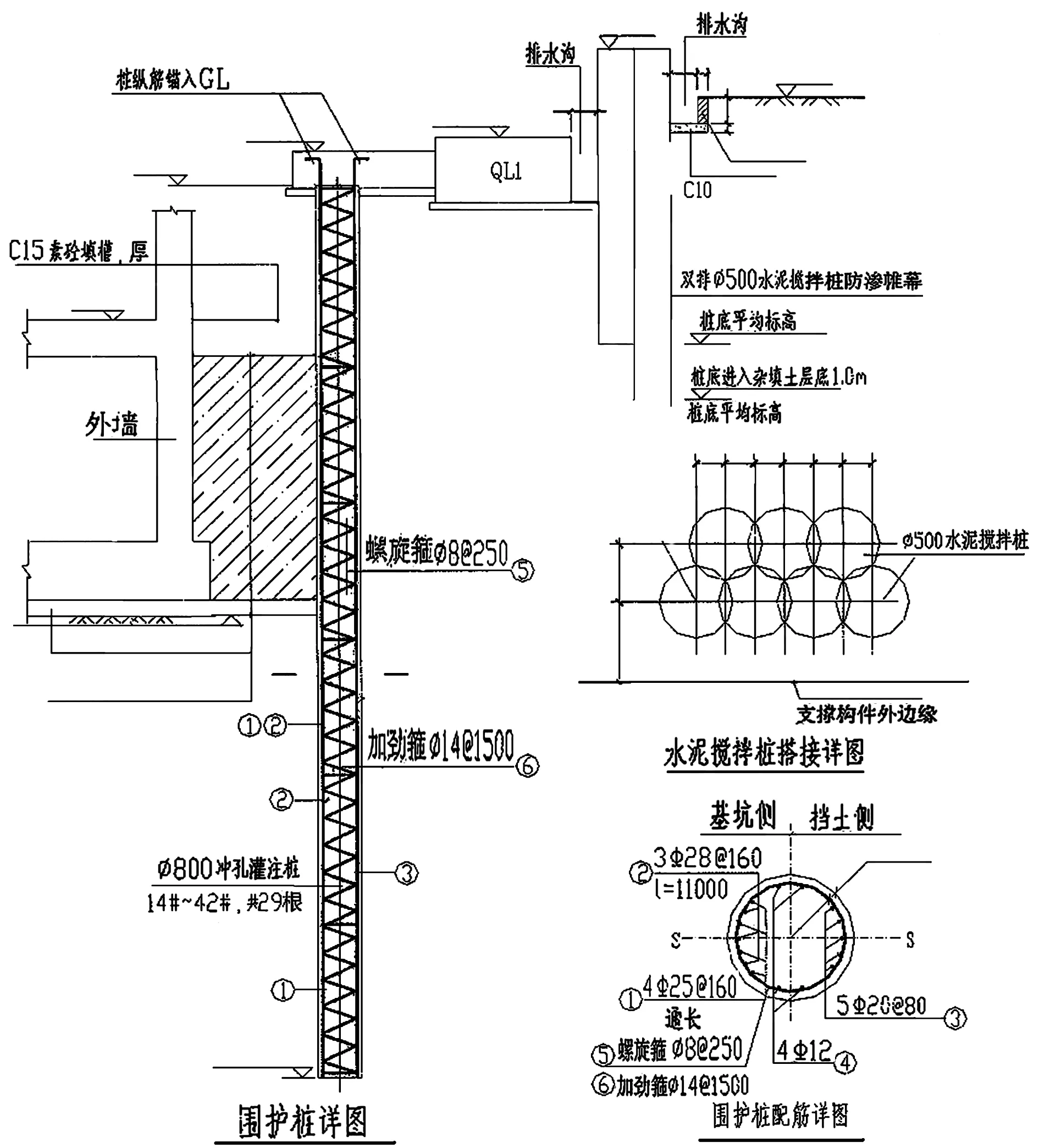
图2 围护桩结构示意图
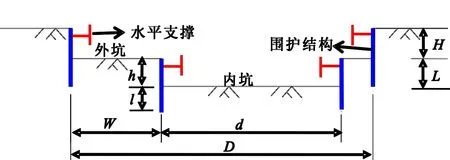
图3 坑中坑式内撑支护基坑几何模型

图4 数值计算模型
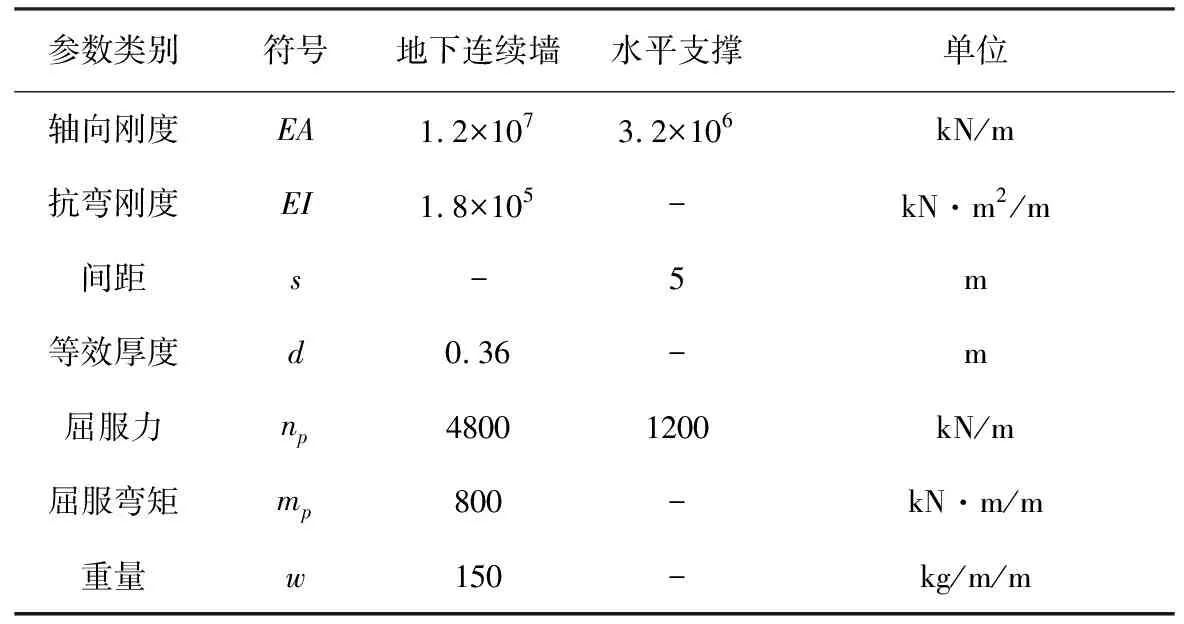
参数类别符号地下连续墙水平支撑单位轴向刚度EA1.2×1073.2×106kN/m抗弯刚度EI1.8×105-kN·m2/m间距s-5m等效厚度d0.36-m屈服力np48001200kN/m屈服弯矩mp800-kN·m/m重量w150-kg/m/m
4 结果分析
4.1 坑距比
定义内外坑坑壁距离与基坑开挖宽度比值为坑距比 。图5给出了不同坑距比对坑中坑式基坑内外坑主动土压力分布模式的影响。可以发现,外坑围护结构主动土压力沿其深度大致呈非线性增大,且形如“锯齿状”。此外,坑距比对土压力分布模式影响并不明显,这与文献[3]结论一致。

图5 坑距比对外坑主动土压力分布模式的影响
图6描述了α对外坑最大主动土压力Eα,max的影响。可以得到,Eα,max随着的增加逐渐增大至趋于稳定,当α时,Eα,max约为130kPa,此后继续增大α,Eα,max值变化不明显,说明此时内坑存在对外坑围护结构作用主动土压力的影响保持不变。

图6 坑距比对外坑最大主动土压力值的影响
图7说明了不同坑距比α对外坑围护结构被动土压力Ep分布模式的影响。从中可以发现,外墙被动土压力在淤泥层随墙体深度近似呈非线性增加,当围护结构进入下一土层(④粉砂夹淤泥层),Ep值反而为不规律减少分布,Ep分布模式总体亦呈“锯齿状”变化。另外,观察图6可以发现归一化深度0.7,对应埋深0.56(H+L),为外坑围护结构的临界深度,当围护结构埋深大于临界值时,被动土压力随坑距比的增加而减少,低于临界值则相反。对于本工况,围护结构0.56(H+L)处距地表-7m处,该深度处内坑设有水平支撑一道,这说明内坑设置水平支撑将改变外坑被动土压力的分布模式,且坑距比越小,水平支撑支挡效果越明显,水平支撑轴力越大,分担荷载越多,因此支撑下部土压力总和将随之减少。

图7 坑距比对外坑被动土压力分布模式的影响

图8 坑距比对外坑最大被动土压力值的影响
图8给出了坑距比变化对外坑围护结构最大被动土压力Ep,max值的影响。类似于主动土压力最大值,Ep,max随着α的增大逐渐增加,后趋于稳定。当α=0.2时,Ep,max=160kPa,进一步增加α,Ep,max几乎保持不变,说明α≤0.2时,改变坑距比对基坑有较明显的影响。
4.2 内外坑深度比

内外坑深度比对外坑主动土压力的影响图9 内外坑深度比对外坑主动土压力分布模式的影响

图10 内外坑深度比对外坑最大主动土压力的影响
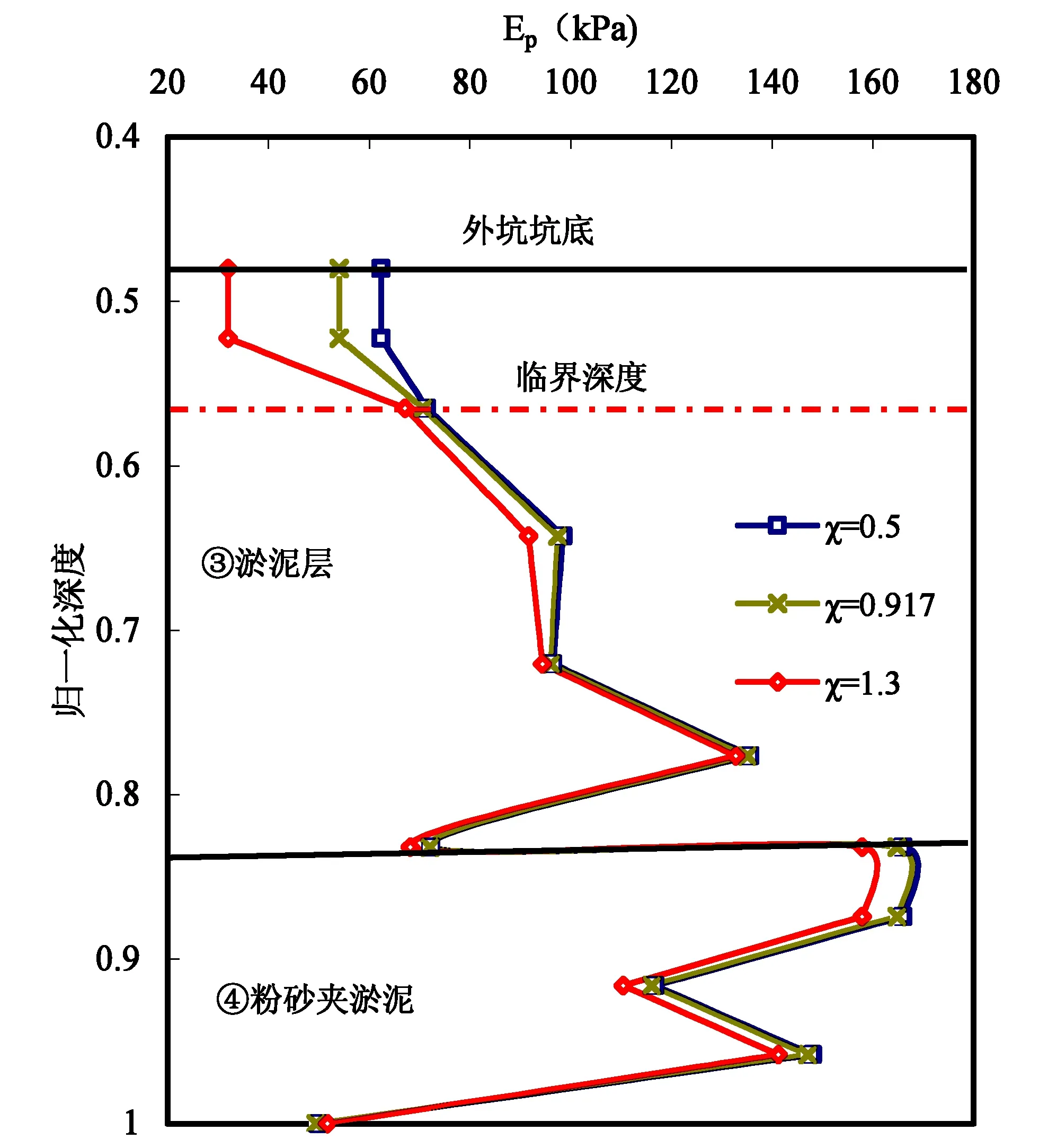
图11 内外坑深度比对外坑被动土压力分布模式的影响
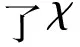
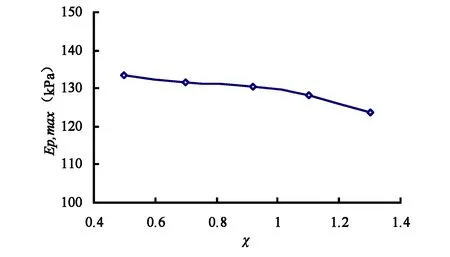
图12 外坑深度比对外坑最大被动土压力值的影响
5 结论
依托某大型公共建筑物,通过有限元数值软件Optum G2,基于平面应变条件,建立了可以考虑坑中坑影响的内撑支护基坑模型,重点分析了坑距比与内外坑深度比对外坑主动土压力和被动土压力分布规律的影响,得到以下结论:
(1)针对坑中坑式内撑基坑,外坑主动、被动土压力均沿围护结构深度增加呈不规律的“锯齿状”增加,水平支撑的设置可减少围护结构主动土压力,有利于控制基坑变形及增强基坑的稳定性。
(2)内坑位置(坑距比)及开挖深度(内外坑深度比)对外坑主动土压力和被动土压力分布模式,总体影响不明显。
(3)坑距比及深度比,对外坑主动土压力影响不明显;对被动土压力有较明显的影响,且存在临界深度(与水平支撑的设置有关)。当围护结构埋深高于临界深度时,坑距比、深度比越大,越小或低于临界深度时则相反。