颗粒增强金属基复合材料的强化机理研究现状

叶想平，李英雷，翁继东，蔡灵仓，刘仓理

(1 中国工程物理研究院流体物理研究所 冲击波物理与爆轰物理重点实验室，四川 绵阳 621999；2 中国工程物理研究院，四川 绵阳 621999)

纯金属具有良好的延展性，但屈服强度较低；氧化物、碳化物、氮化物等硬质陶瓷(如Al2O3,SiC,BN)具有高强度，但延展性极差[1]。将这两种材料结合在一起形成的颗粒增强金属基复合材料[2-3]具备高屈服强度和较好的延展性。从20世纪60年代以来，已在先进战机、汽车工业、航空航天、核能和船舶工业中都得到了广泛应用[4-7]，并且应用范围还在进一步扩大[6-8]。目前，已经发展出铝基[4,9-10]、镁基[3,11-12]、钛基[8,13]、铜基[13]等系列金属基复合材料。

颗粒增强金属基复合材料的众多物理、力学性能参量中，屈服强度是非常重要的一项基础性能参量。如何提高颗粒增强金属基复合材料的屈服强度，并在一定程度上兼顾材料的延展性一直是研究者努力的方向[5,14-15]。颗粒增强金属基复合材料的屈服强度受Orowan强化应力[4,16]、位错强化应力[17-18]、颗粒承载应力[19]、晶界强化应力[20-21]、晶格摩擦应力[22-23]和固溶强化应力[24]的控制。其中，Orowan强化、位错强化和颗粒承载强化是颗粒增强金属基复合材料中最主要、也是最常使用的3种强化机制[17,25-27]。例如：提高颗粒体积分数、细化颗粒尺寸、使颗粒均匀分布能够提高Orowan强化应力和位错强化应力[4,16,25,28-29]；提高颗粒体积分数、采用颗粒包围金属基体的微观非均匀分布状态能够提高颗粒承载强化应力，尤其是调控颗粒包围金属基体还能够进一步提高颗粒增强金属基复合材料的延展性[27,30-31]。

本文从颗粒增强金属基复合材料研究角度综述了Orowan强化应力、位错强化应力和颗粒承载强化应力对复合材料屈服强度影响的研究现状和存在的问题。总结了提高Orowan强化应力、位错强化应力和颗粒承载强化应力的方法。另外，对晶界强化应力、晶格摩擦应力和固溶强化应力也作了简要介绍。

1 Orowan强化应力理论

1.1 基础理论

Orowan强化应力是滑移位错被颗粒阻挡，并迫使其绕行通过而引起的强化应力[32]。其概念最早由Orowan[32]在1948年提出，滑移位错被颗粒阻挡以后，发生弓弯平衡外部载荷；当外部载荷进一步增加以后，滑移位错以绕行方式通过颗粒，并在颗粒周围留下位错环，如图1所示[4,16]。图中D为阵列排布颗粒被滑移面切割的等效直径，L为阵列排布颗粒被滑移面切割的等效表面间距，颗粒中心间距λ=D+L。当颗粒体积分数较高时，位错滑移变得较为困难，难以绕行通过颗粒[2,33]。因此，Orowan强化应力只在较低体积分数时对复合材料屈服强度的提高有较为明显的影响。

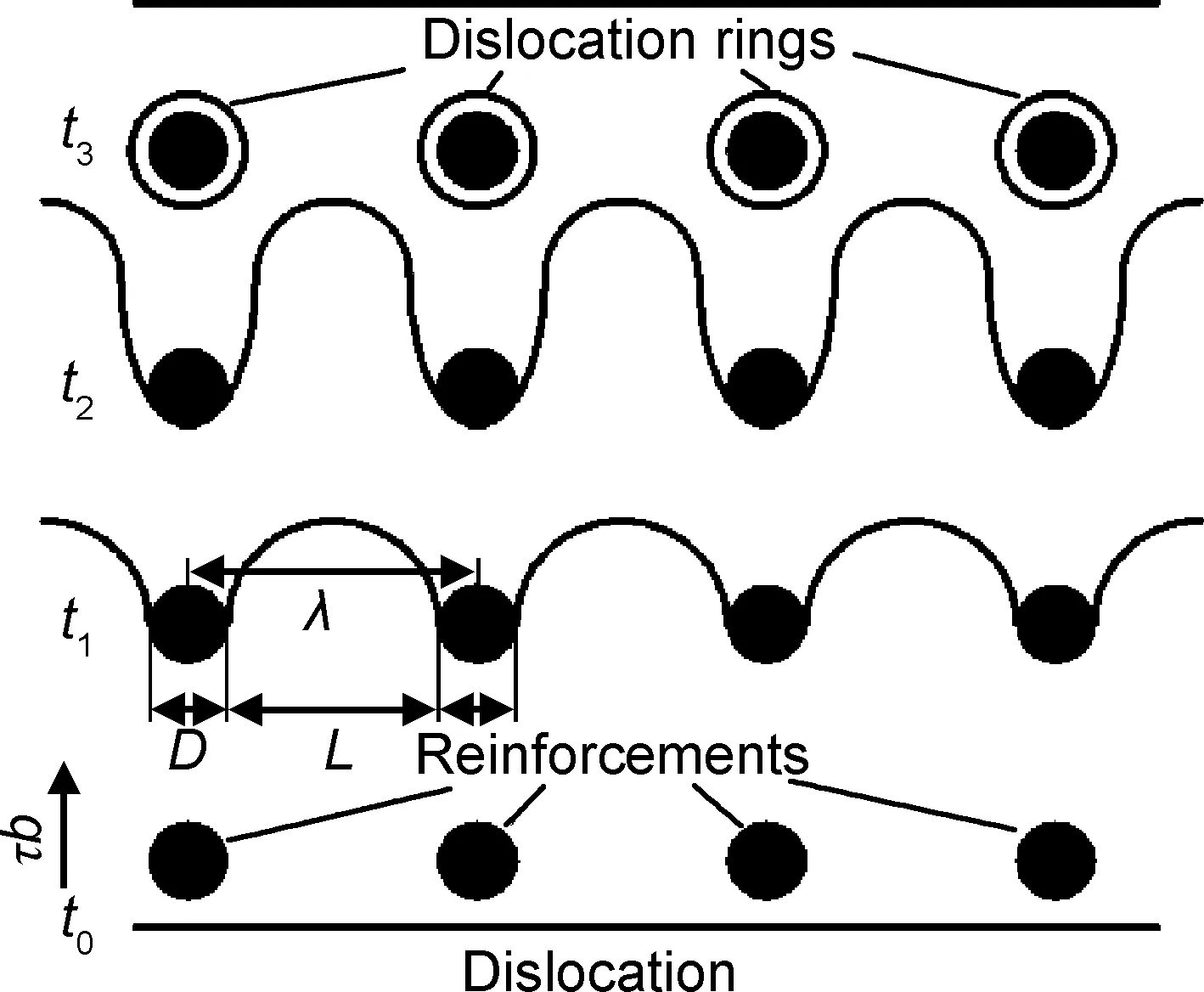
图1 位错绕行通过增强颗粒示意图[34]Fig.1 Schematic diagram of dislocation bypassing reinforcements

Orowan强化应力如公式(1)所示[32,34-35]。其中，G，b分别为金属基体剪切模量和伯格矢量。r0为位错心半径(r0=b[24])，ν为泊松比。η为与颗粒分布状态有关的常数，当颗粒以阵列形式排布时，η=1[36]；当颗粒均匀分布(非阵列排布)时，η=0.85[4,37]。M为Taylor系数，对应于FCC和BCC金属M分别取3.06，2.6[24]。

(1)

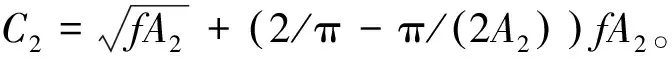
表1 Orowan方程参数计算式Table 1 Parameters of the Orowan strengthening formula

1.2 颗粒体积分数对Orowan强化效应的影响

理论上颗粒体积分数越高，Orowan强化应力越大。例如：半径为0.1μm的球形氧化铝颗粒阵列排布于铝基体内，结合公式(1)以及表2中铝基体力学参数(E，α，Tprocess，Ttest分别为杨氏模量、热膨胀系数、制备温度和实验温度)计算得到的Orowan强化应力值与颗粒体积分数关系如图2所示，Orowan强化应力理论值随球形颗粒体积分数的增加而增大。

表2 铝和氧化铝颗粒性能参数表[25]Table 2 Parameters of the aluminium and alumina particles[25]

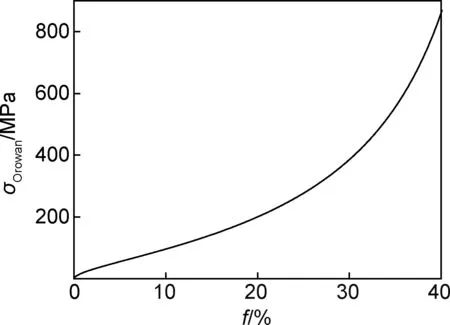
图2 球形颗粒体积分数与Orowan强化应力理论值的关系Fig.2 Relationship of volume fraction of spherical particle and theoretic Orowan strengthening

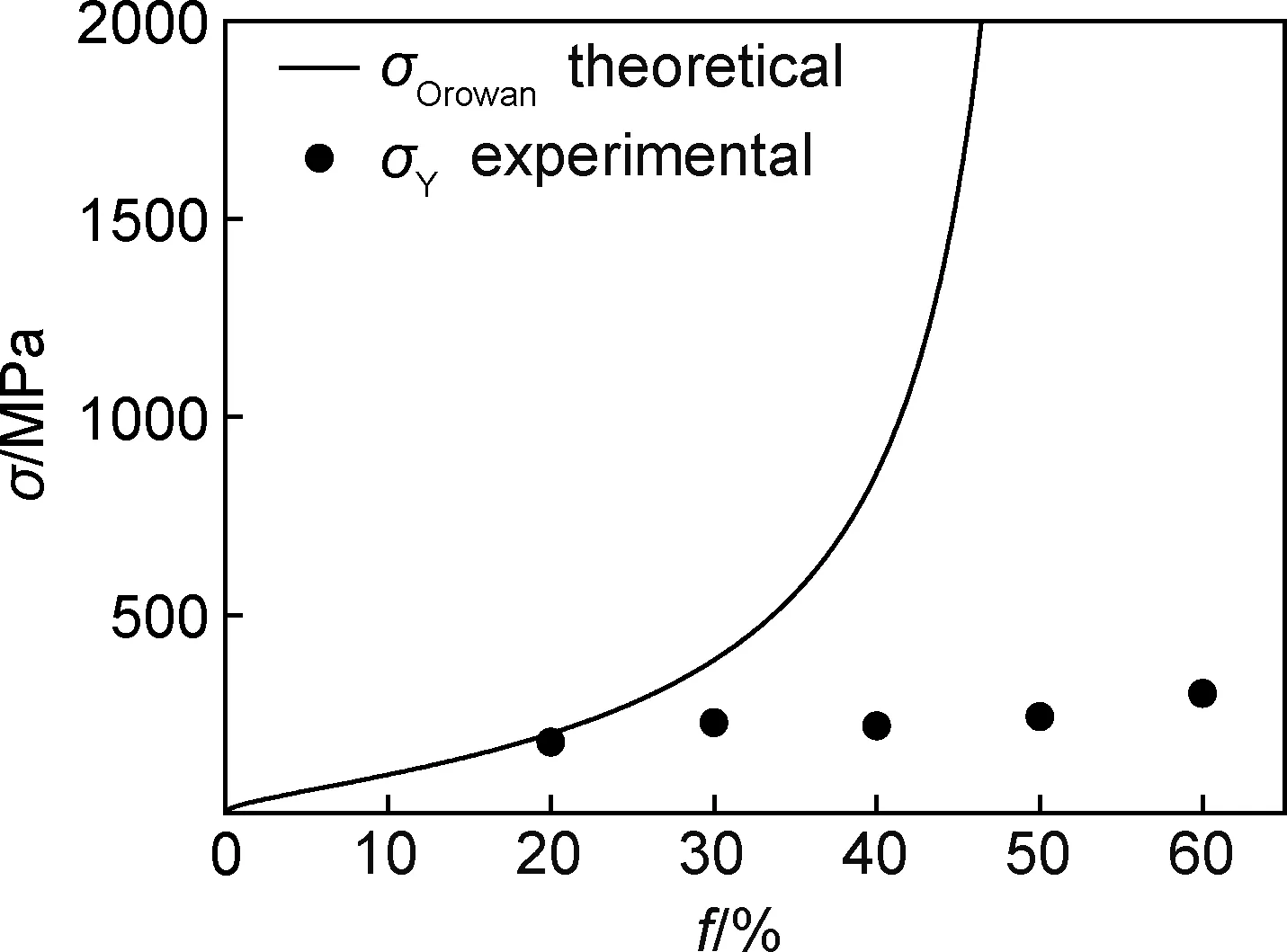
图3 增强铝屈服强度和Orowan强化应力与球形氧化铝颗粒体积分数关系[33]Fig.3 Relationship of yield with Orowan strengthening of aluminium matrix composites with volume fraction of spherical Al2O3 particle[33]

1.3 颗粒分布状态对Orowan强化应力的影响

在较低颗粒体积分数范围内(f≤14%)，颗粒非常均匀地分布于金属基体内，能够获得接近理论值的Orowan强化应力，从而提高颗粒增强金属基复合材料屈服强度。例如：Chen等[3]制备出一种体积分数为14%的SiC纳米颗粒增强Mg2Zn基复合材料。直径60nm的球形SiC颗粒非常均匀地分布于镁基体内，并且这种均匀分布状态可长时间保持而不发生颗粒聚集，如图4所示[3]。通过微观压缩实验证实添加纳米颗粒后的Mg2Zn基复合材料屈服强度提高1倍左右，如图5所示，其中，Orowan强化应力为113MPa[3]。但Chen等[3]目前只能制备出这种纳米颗粒均匀分布的直径几微米的样品，无法制备更大体积的样品。这也表明，即便在较低颗粒体积分数范围内，使颗粒非常均匀分布对材料制备工艺也存在极大的挑战。

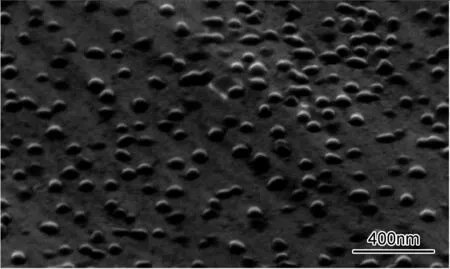
图4 SiC纳米颗粒均匀分布于Mg2Zn基体扫描电镜图[3]Fig.4 SEM image of the uniform distribution of SiC nanoparticles in the Mg2Zn matrix[3]

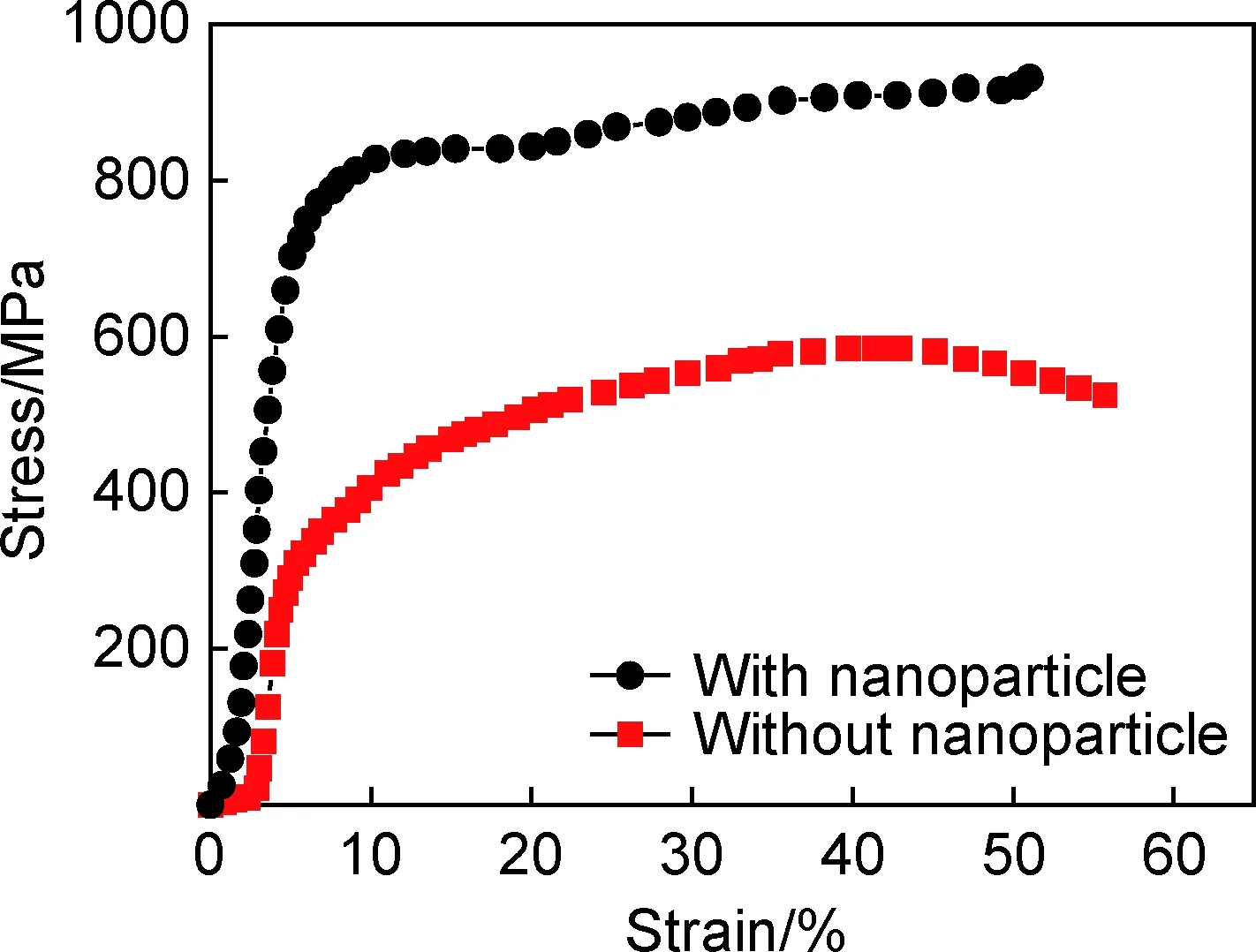
图5 Mg2Zn合金室温压缩应力-应变曲线[3]Fig.5 Compressive stress-strain curves of Mg2Zn alloys at room temperature[3]

在较低颗粒体积分数范围内，当颗粒分布状态达不到Orowan强化应力理论模型要求时，也将导致Orowan强化应力实验值远小于理论值。例如：Morteza等[25]研究了纳米颗粒增强铝基复合材料屈服强度与颗粒体积分数的关系。增强铝屈服强度随颗粒体积分数的增加而增大，在低体积分数(f=1%)条件下增强铝屈服强度理论值与实验值基本重合；但随着颗粒体积分数的增加，增强铝屈服强度理论值与实验值的差异越来越大，在体积分数为4%时增强铝屈服强度理论值甚至比实验值高50%左右，如图6所示[25]。增强铝屈服强度实验值与理论值的差距随颗粒体积分数的增加而增大的主要原因之一是颗粒发生聚集的程度随颗粒体积分数的增加而增大(等价于颗粒尺寸增大)，降低了Orowan强化应力[25]。

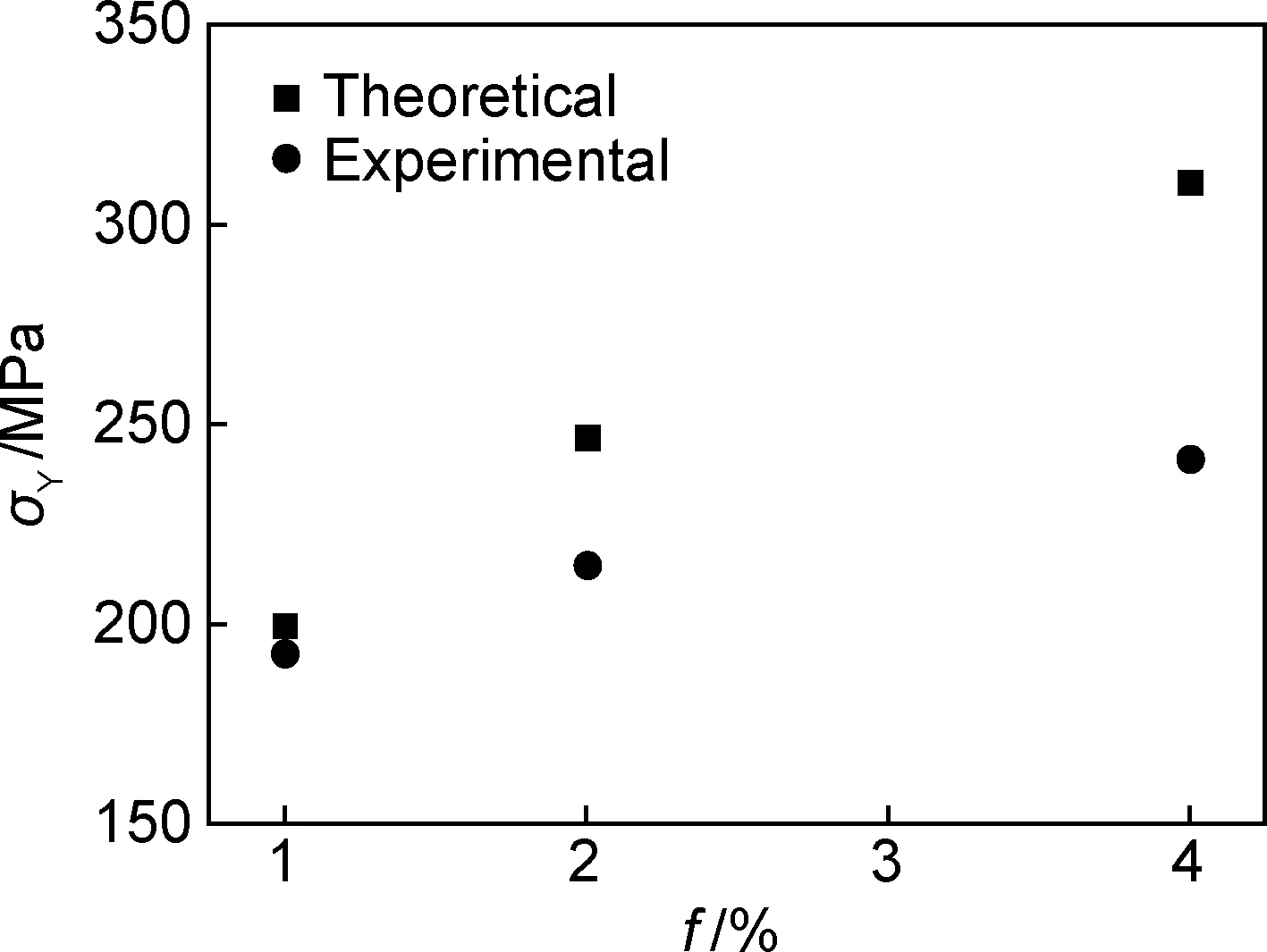
图6 不同体积分数的Al/Al2O3-B4C增强铝屈服强度[25]Fig.6 Yield strength for the Al/Al2O3-B4C nano-composites with different volume fractions[25]

1.4 颗粒尺寸对Orowan强化应力的影响

即便在较低颗粒体积分数条件下(f≤14%)，现有复合材料制备工艺水平也难以使颗粒均匀分布于金属基体内[3,25]，因此，降低颗粒尺寸成为提高Orowan强化应力的重要途径。Orowan强化应力随颗粒尺寸的减小而增大，直至达到颗粒尺寸临界值rc=2π·Gb/Gp[24]，其中，Gp为增强相剪切模量。通常rc小于1nm，因此，普通颗粒增强金属基复合材料中的颗粒尺寸均大于临界尺寸[17,25]。结合公式(1)和表2中的参数计算可得体积分数为10%的球形氧化铝颗粒增强铝基复合材料中Orowan强化应力与颗粒尺寸关系，如图7所示。Orowan强化应力随颗粒尺寸的减小而增大，当颗粒尺寸进入纳米尺度(rp<100nm)后，Orowan强化应力开始随颗粒尺寸的减小急剧增加。因此，近年来大量研究人员致力于研究低体积分数的纳米颗粒增强金属基复合材料，并获得了一系列较高屈服强度的复合材料[3,25]。例如：Morteza等[25]制得的半径为25nm、体积分数为4%的Al2O3/SiC4颗粒增强铝的屈服强度便达到310MPa，是纯铝屈服强度的10倍左右；Chen等[3]制得的半径30nm，体积分数为14%的SiC颗粒增强Mg2Zn基复合材料屈服强度(710MPa)是未经颗粒增强Mg2Zn基体屈服强度的两倍。

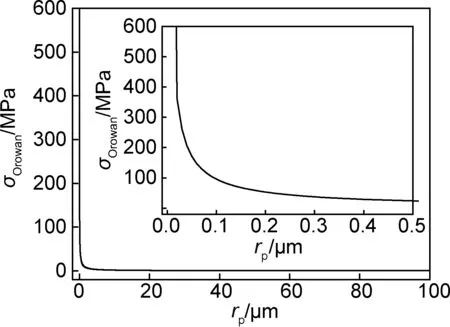
图7 球形颗粒尺寸与Orowan强化应力关系图Fig.7 Relationship of Orowan strengthening and the size of spherical particle

1.5 颗粒尺寸分布状态对Orowan强化应力的影响

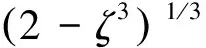
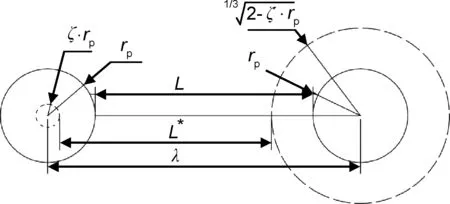
图8 颗粒尺寸不均匀示意图Fig.8 Schematic diagram of the inhomogeneity of particle size

2 位错强化应力理论

金属基体内部位错之间相互割接、交叉等阻碍滑移位错运动引起的强化应力即为位错强化应力，计算式如公式(2)所示[17-18]:

ΔσD=αDGbρ1/2

(2)

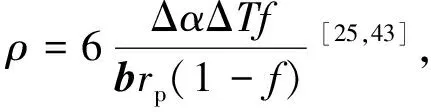
在美国， Kronospan公司决定进一步增加1.01亿美元对亚拉巴马州牛津的投资，共计达4.63亿美元。该扩张计划最初是在2016年年中宣布的，投资额为3.62亿美元，包括两条强化地板及浸渍纸装饰生产线、一条刨花板及热熔胶合层压生产线，以及合成树脂厂的扩建。

增强颗粒尺寸越小、体积分数越大引起的颗粒与金属基体界面位置的位错增量越大，相应的位错强化应力也越大。对于普通微米级颗粒增强金属基复合材料而言，这种界面位置热膨胀系数差异引起的强化应力值较小。例如：根据公式(2)和界面位置位错密度增量计算式，结合表2中铝基体和氧化铝颗粒性能参数计算可得，体积分数为10%、半径为10μm的球形氧化铝颗粒增强铝内部位错强化应力仅为13MPa。但同样体积分数半径为10nm的球形氧化铝颗粒引起的位错强化应力高达400MPa。因此，位错强化应力是纳米颗粒增强金属基复合材料中非常重要的一项强化应力，也是近年研究人员研究纳米颗粒增强金属基复合材料的一个重要原因[3,25]。

根据位错密度增量计算式以及公式(2)可知，当颗粒随体积分数增加而发生聚集时(等价于增加颗粒尺寸)，也将显著降低位错强化应力。因此，颗粒聚集将同时降低Orowan强化应力和位错强化应力，从而降低复合材料的屈服强度[25]。

3 颗粒承载强化应力理论

3.1 颗粒离散分布的承载强化应力

增强颗粒直接承受金属基体传递的载荷即为颗粒承载强化应力[26,43]。当颗粒离散分布时，颗粒承载强化应力计算式如公式(3)[19]所示：

ΔσLoad=0.5fσm

(3)

式中：σm为未经颗粒增强的金属基体屈服强度[43]。提高颗粒体积分数能够提高颗粒承载强化应力，在本文讨论的颗粒体积分数范围内(f≤14%)，离散分布颗粒的承载强化应力值很低，不超过未经颗粒增强金属基体屈服强度的10%。

3.2 颗粒微观非均匀分布的承载强化应力

当颗粒呈微观非均匀分布时，尤其是颗粒在富集区发生直接相互接触时，能够进一步提高颗粒承载强化应力。但长期以来人们一直努力使颗粒更加均匀地分布于金属基体内。然而，越来越多的研究结果表明[8,46-49]，这种方法虽然能够提高颗粒增强金属基复合材料屈服强度，但却难以达到最佳效果，而且还导致复合材料延展性急剧降低，严重限制了颗粒增强金属基复合材料的应用[27,49]。20世纪60年代，Hashin和Shtrikman等[48,50]提出的H-S理论指出两相复合材料中增强颗粒均匀分布只对应于弹性性能的理论下限值，增强颗粒包围在金属基体周围才能够达到弹性性能的理论上限值，如图9所示。

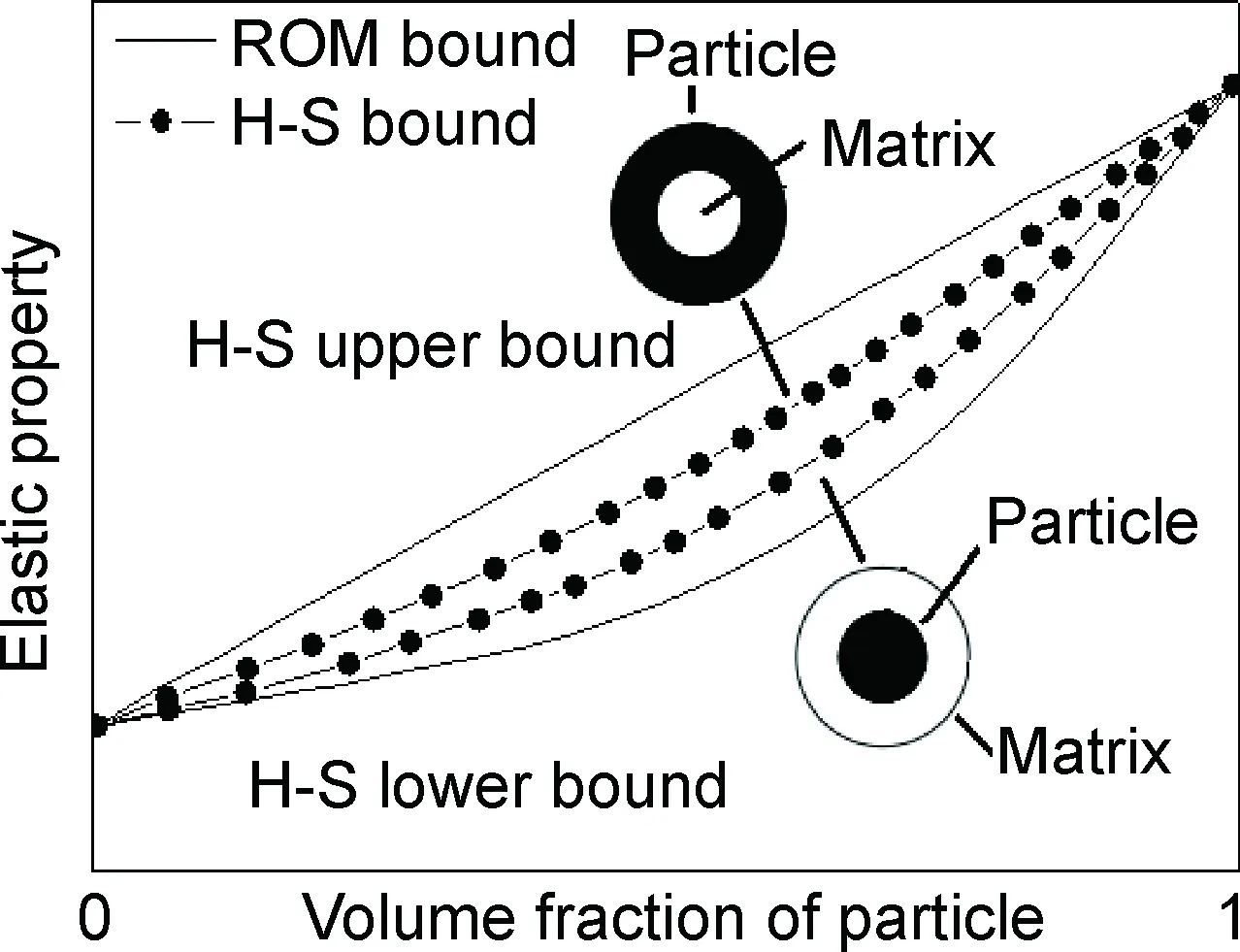
图9 弹性性能与颗粒体积分数关系[50]Fig.9 Relationships of elastic property and volume fraction of particle[50]

此后，国内外研究人员设计出了大量增强颗粒呈微观非均匀分布的组织结构，以实现颗粒包围金属基体的结构特征[8,51]。4种典型的增强颗粒包围金属基体的分布示意图如图10所示[27,51]，黑点代表增强颗粒，白底代表金属基体。其中，以黄陆军等[8,27,30-31,52]和Kaveendran等[53]制得的一系列颗粒呈网络状分布的复合材料最具代表性，也最符合颗粒包围金属基体的结构要求。例如：Kaveendran等[53]制得的体积分数为10%的Al2O3/Al3Zr颗粒呈网络状包围铝基体的增强铝扫描电镜显微图如图11(a)所示，白点为增强颗粒，M区为含极少增强颗粒的颗粒贫化区。实验结果表明，这种颗粒呈网络状分布的增强铝屈服强度比颗粒均匀分布的增强铝提高了4%，延展性提高了76.9%，如图11(b)所示[53]。颗粒由微观均匀分布调控为网络状分布不仅能够进一步提高复合材料的屈服强度，还能够提高复合材料的延展性[31]。

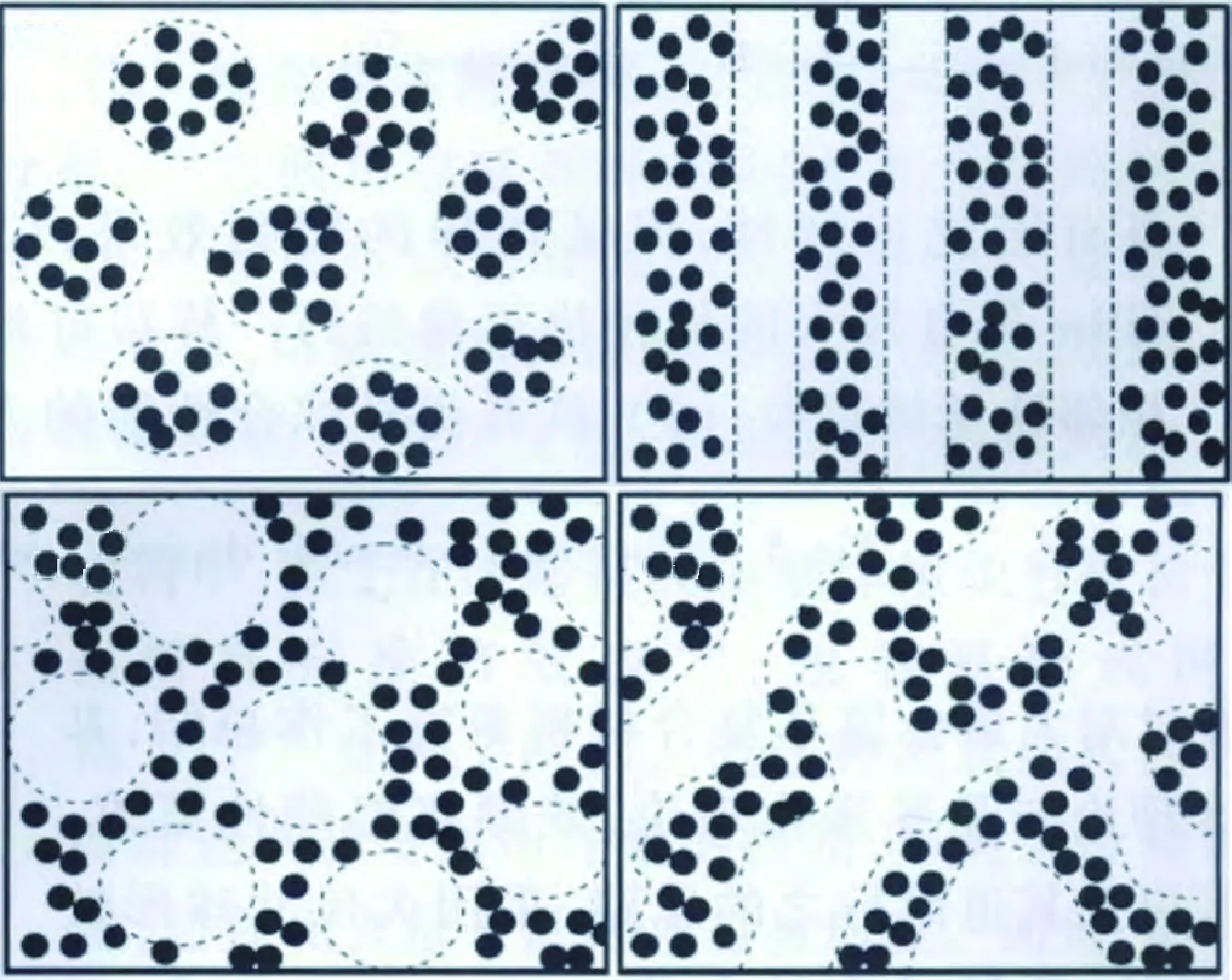
图10 颗粒微观非均匀分布的4种组织结构示意图[27,51]Fig.10 Schematic illustrations of microstructural inhomogeneity with four different patterns of reinforcement[27，51]

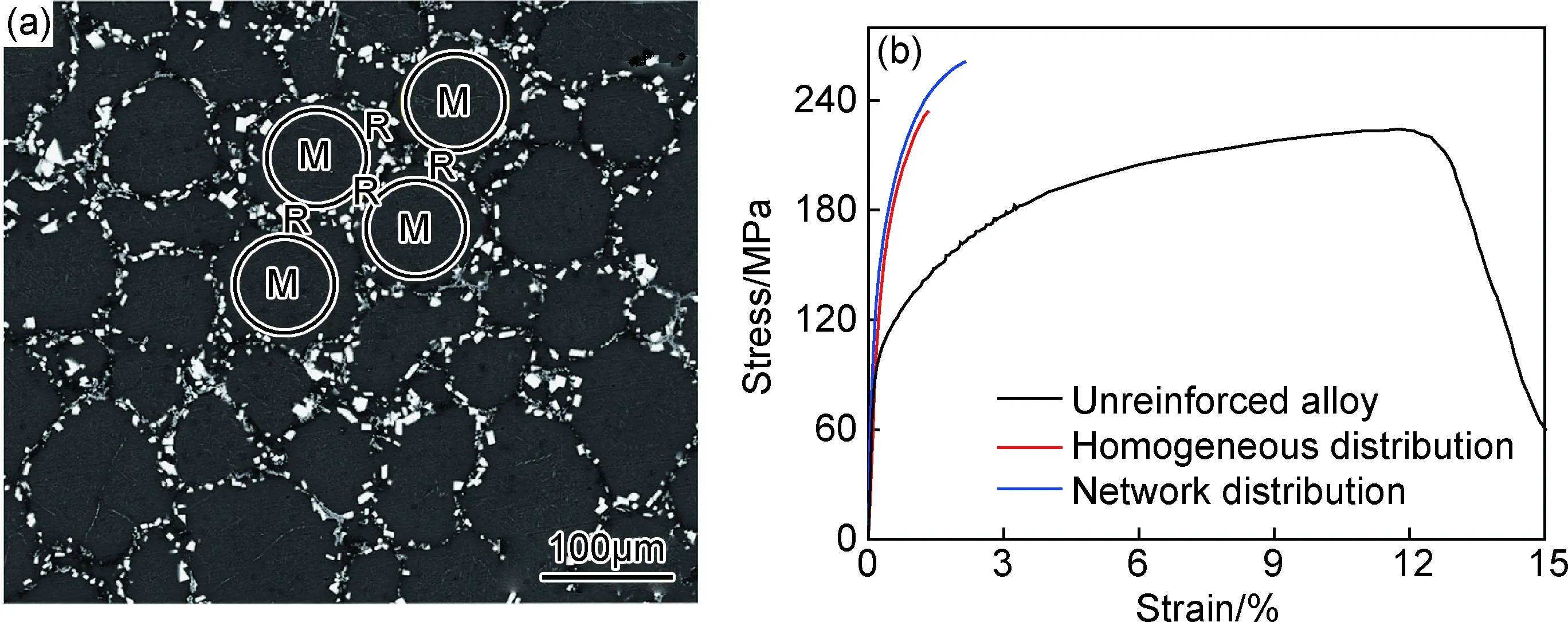
图11 颗粒呈网络状分布的增强铝复合材料[53] (a)扫描电镜显微图;(b)准静态拉伸应力-应变曲线Fig.11 Particles with network structure reinforced aluminum based composites[53](a)SEM morphology；(b)quasi-static tensile stress-strain curve

将颗粒调控呈包围金属基体的非均匀分布状态，主要是通过形成图12所示的增强颗粒准连续分布的“两相复合结构”来提高复合材料的屈服强度和延展性[27,52]。图12中α相区(增强颗粒富集区)内增强颗粒大量直接相互接触以提高颗粒承载强化应力，从而提高复合材料的屈服强度；β相区(增强颗粒贫化区)内增强颗粒很少，保留了金属基体良好的延展性，能够钝化裂纹尖端，降低裂纹扩展速度，从而提高复合材料延展性[27,52]。这种增强颗粒呈微观非均匀分布状态的复合材料制备工艺更为复杂，给量化颗粒承载强化应力，以及对复合材料屈服强度的影响研究带来新的挑战[27,31]。

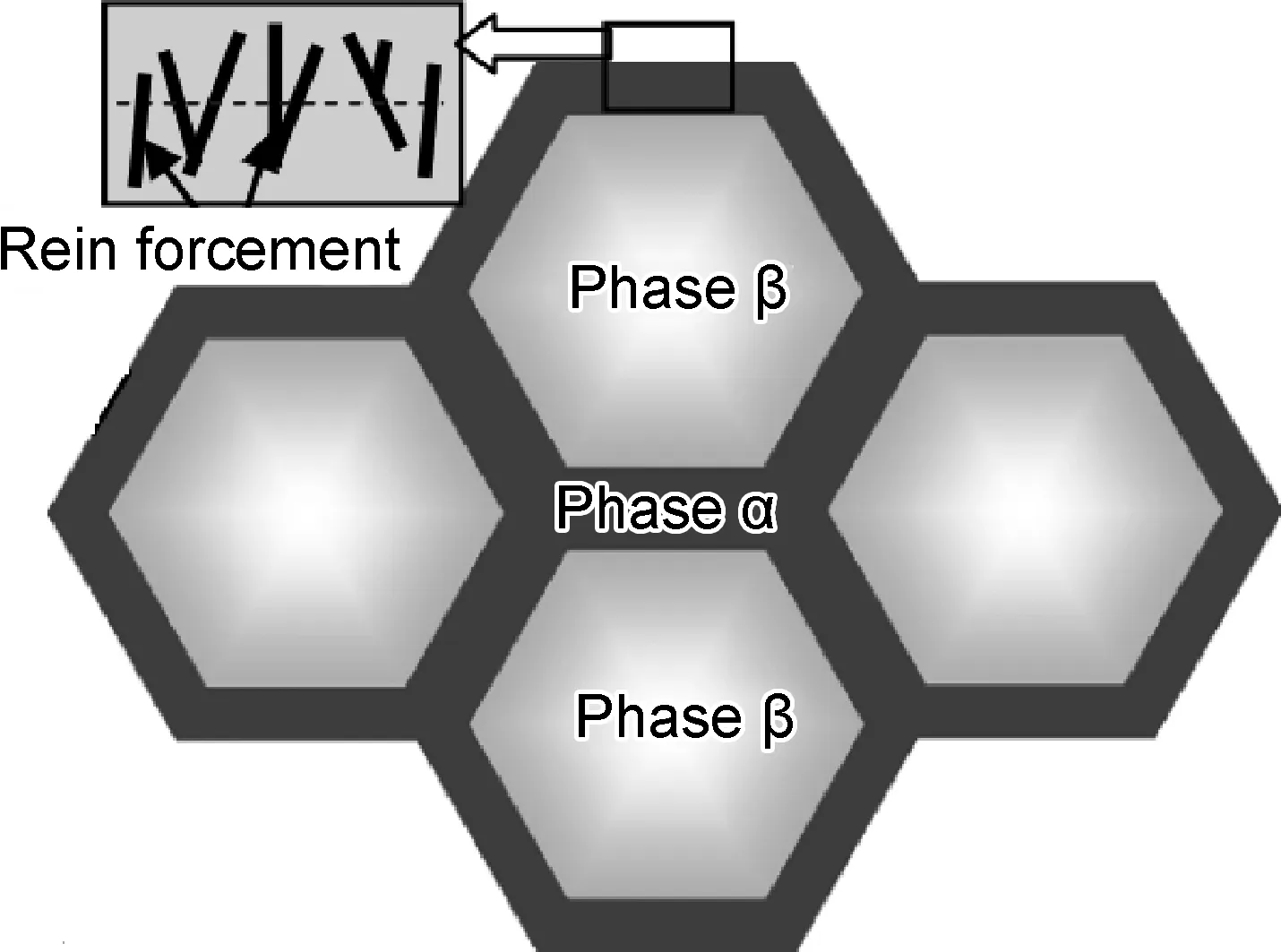
图12 准连续颗粒增强金属基复合材料示意图[27]Fig.12 Schematic diagram of quasi-continuous network microstructure for particle-reinforced metal matrix composites[27]

4 其他强化应力理论

在颗粒体积分数低于14%的范围内，Orowan强化应力、位错强化应力和颗粒承载强化应力是颗粒增强金属基复合材料内部最主要的3种强化应力。除此以外，复合材料内部还存在晶界强化应力、晶格摩擦应力和固溶强化应力。

4.1 晶界强化应力

晶界阻碍滑移位错运动，导致位错在晶界堆积引起的强化应力即为晶界强化应力[20-21]。最早由Hall[20]和Petch[21]研究软钢时提出，后被推广应用到众多金属材料研究中，并被大量实验结果所证实。晶界强化应力计算式，也称H-P关系式，如公式(4)所示[20-21]：

ΔσGB=kH-Pd-1/2(d>100nm)

(4)

式中：ΔσGB为晶界强化应力；d为平均晶粒尺寸；kH-P为与晶界特性有关的晶界强化系数。降低颗粒尺寸、提高晶界强化系数能够提高晶界强化应力[54-55]，但在颗粒增强金属基复合材料研究中，晶界强化并不是最主要的强化机制，晶界强化应力相对Orowan强化应力、位错强化应力和颗粒承载强化应力往往也较低[27,56]。晶界强化应力很多时候甚至和晶格摩擦应力等一起被当作未经颗粒增强金属基体屈服强度的一种影响机制，而不单独讨论[12,26,56]。

4.2 晶格摩擦应力

晶格摩擦应力Δσ0是材料内部固有的周期排布晶格对滑移位错的阻碍应力，与材料晶体结构、位错密度、位错滑移速率，以及环境温度都有关[19,57]。晶格摩擦应力包含两部分内容：(1)周期排布晶格原子对滑移位错的阻碍应力(也叫P-N力[22-23])，0K温度下金属基体的P-N力如公式(5)所示:

(5)

4.3 固溶强化应力

溶质原子融入金属基体后导致晶格畸变，增加滑移位错运动阻力，引起的强化应力即为固溶强化应力[24]。均匀固溶强化应力如公式(6)所示[4,24]：

ΔσSS=MASSCβSS

(6)

式中：C为固溶原子质量分数；ASS，βSS=2/3[24]均为材料常数；ASS取值一般不超过20MPa[4,17]。颗粒增强金属基复合材料选用的增强颗粒通常为难溶于金属基体的氧化物、氮化物等颗粒[60-61]，C值通常低于0.001[62]，因此，增强颗粒引起的固溶强化应力一般低于0.6MPa，可以忽略。

5 各项强化应力的相互耦合关系

叠加以上各项强化应力可获得颗粒增强金属基复合材料的屈服强度σy。但目前各项强化应力之间的耦合关系存在线性叠加[16,63]、乘积叠加[19,26,43]和均方根叠加[17,64]3种形式。虽然这3种叠加关系均缺乏严密的物理基础[65]，但都得到了一定程度的应用。

5.1 线性叠加

线性叠加认为各项强化应力场之间相互独立，复合材料屈服强度值为各项强化应力值的线性叠加之和，如公式(7)所示[16,63]。线性叠加关系只适用于具有少数几种强化机制的纳米颗粒增强金属基复合材料研究[16,43,63]。

σy=Δσ0+ΔσGB+ΔσOrowan+ΔσD+ΔσLoad

(7)

5.2 乘积叠加

乘积叠加关系认为各项强化应力之间服从乘积耦合关系，如公式(8)所示[19,26,43]：

σy=(Δσ0+ΔσGB)(1+fOrowan)(1+fD)(1+fLoad)

(8)

式中：fOrowan=ΔσP/(Δσ0+ΔσGB)，fD=ΔσD/(Δσ0+ΔσGB)，fLoad=ΔσLoad/(Δσ0+ΔσGB)分别为各项强化应力的强化系数。乘积叠加关系也只适用于纳米颗粒增强金属基复合材料的研究[25-26]，采用乘积叠加关系计算得到的复合材料屈服强度值能够更好地与实验结果吻合，也是目前纳米颗粒增强金属基复合材料研究中应用最为广泛的叠加关系[26,56,65]。

5.3 均方根叠加

均方根叠加认为各项强化应力之间服从均方根耦合关系，如公式(9)所示[4,17]。均方根叠加关系主要应用于微米级颗粒增强金属基复合材料研究[17,43]。

(9)

6 结束语

在本文讨论的颗粒体积分数范围内(f≤14%)，Orowan强化、位错强化和颗粒承载强化是颗粒增强金属基复合材料内部最主要的3种强化机制。

(1)Orowan强化应力和位错强化应力随颗粒体积分数的增加、颗粒尺寸的减小以及颗粒分布状态均匀性的提高而增加，Orowan强化应力还受颗粒尺寸均匀性的影响。

(2)调控颗粒呈包围金属基体的微观非均匀分布状态，能够进一步提高颗粒承载强化应力，从而提高复合材料的屈服强度，还能够提高复合材料的延展性，但颗粒呈微观非均匀分布的制备工艺更为复杂，给量化颗粒承载强化应力，以及对复合材料屈服强度的影响研究也带来新的挑战。

叠加以上各项强化应力能够获得颗粒增强金属基复合材料的屈服强度。但各项强化应力之间存在线性叠加、乘积叠加和均方根叠加3种耦合形式。线性叠加和乘积叠加适用于纳米颗粒增强金属基复合材料研究，其中乘积叠加计算得到的复合材料屈服强度值能够与实验值更好地吻合，应用也更广。均方根叠加关系主要应用于微米级颗粒增强金属基复合材料的研究。