呈现知识生成过程的全国卷高考数学试题探究——以一道数列题目为例

（四川省泸州市泸州老窖天府中学 四川泸州 646000）

一、背景分析

《普通高等学校招生全国统一考试大纲》从“知识要求”、“ 能力要求”、“个性品质要求”、“考查要求”四个方面对考生和高考试卷提出了要求。 其中，“知识要求”的理解层面提到“对所列知识内容有较深刻的理性认识，知道知识间的逻辑关系”；掌握层面提到“能够对所列的知识内容进行推导证明”。“考查要求”中提到“对数学基础知识的考查，既要全面又要突出重点。注重学科的内在联系和知识的综合性，不刻意追求知识的覆盖面。”可见，高考试题对学生的要求不仅仅是会用知识，还需全面把握知识。而对知识的把握，重要的一个环节就是了解知识的生成过程。

二、一个经典题目的分析

纵观这几年的高考全国卷，2017年全国卷III的数列解答题的第一问，对知识生成过程的考查，是个经典的例子。此题出现在解答题的第一题第一问，着实让很多考生猝不及防。说此题前，我们先来说说整个高中要求学生掌握的数列公式的逻辑线。

数列知识从一列数起源，找到规律，利用不完全归纳法得出等差数列、等比数列通项公式。其中，等差数列是后一项在前一项的基础上不断地加同一个数（即公差，通常用字母d表示），因此等差数列通项公式是等比数列通项公式（q 是指公比）的推导原理类似。除了研究通项公式，我们还研究前n 项和公式。前n 项和，通常记作Sn，顾名思义，数列的前n 项和是指由此意义，我们还可以知道两式做差，我们可以有如下演算过程：

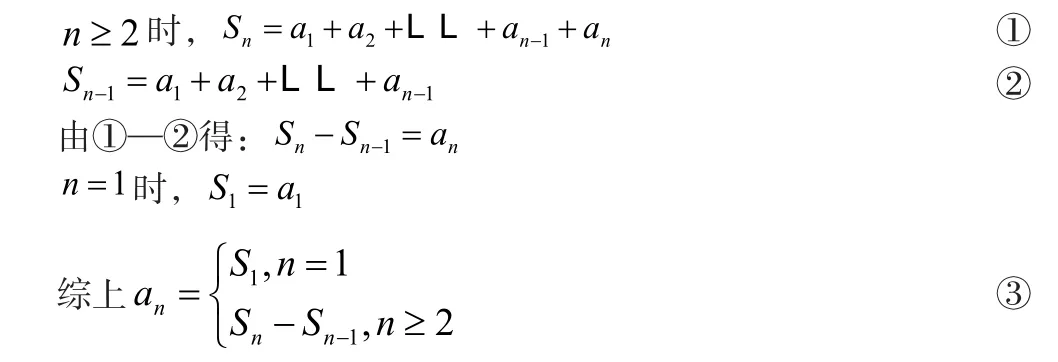
公式③便是已知数列的前n项和，求通项公式时的一个重要公式。

除此以外，利用倒序相加法我们推导出了等差数列的前n项和公式：

将an=a1+(n−1)d 代入化简可得：对此公式进一步整理还可以变形为：

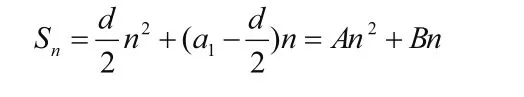
发现d≠0的等差数列前n 项和公式是一个关于n的常数项为0的二次函数。另外，利用错位相减法，也可以推导出等比数列的前n 项和公式：

对此公式进一步整理还可以变形为：

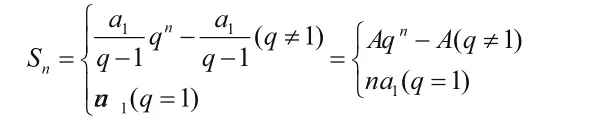
发现q≠1的等比数列前n 项和公式是一个关于n的指数型函数。

理清逻辑线，学生反复推导，掌握并记忆这些公式应该是非常容易的了。下面我们来看看前面提到的2017年全国卷III的17题第一问：

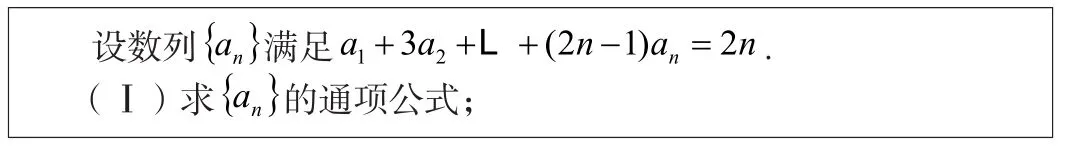
这个题的第一问，让很多学生难以入手，即使对高中所有的数列公式都烂熟于心，也不知道究竟代哪个公式。实际上，题干中的的前n项和。这是一个已知前n 项和，求通项公式的题目，也就是前面提到的公式③。现在我们来尝试解答一下第一问：

这样分析下来，这道高考试题对知识生成过程的呈现真得堪称经典。遗憾的是，此题学生的得分率低，结合笔者一线任教的经历来看，我们能发现现在学生普遍现状是：公式倒背如流，直接代公式的题目也是在反复刷题后得心应手，对知识生成的来龙去脉，对公式的推导过程，却是一知半解，甚至全然无知的。

结合前面说到的《考试大纲》的要求和高考试题的走向，再看看学生现状，下面提一些应对措施，供大家参考，不足之处，请多指教。

三、应对措施

1.教师提高自身数学修养，对高中数学几大知识板块应有更深更广的了解。

2.提高重视程度，放慢教学速度，切实抓好概念课的启发式教学。给学生更多时间和空间，让他们能够独立或者互助地完成公式定理的推导。

3.重视教材正文。教材正文都有完整的推导过程，学生和老师都应更加重视，学生更是应该反复研读，不断提高自身数学素养。教材外的，教师还应适当给学生补充，或者引导学生去补充完善。