高中数学函数与回归方程浅探

（北京师范大学株洲附属学校 湖南株洲 412000）

引言

函数是数学中最为典型的一种关系，这种关系是一种对应性的关系，主要表达的是，当A随着B的变化而变化，那么就可以说A是B的函数，但是具体的函数关系有很多，不同的函数之间的表达式也各不相同。如果我们想要正确的理解认知这些概念，不仅要函数进行表面性的理解，还要学会将函数的理论知识应用到实际的答题过程中进一步的理解其内在含义。回归分析法就是一种解决函数问题的最优选择。

一、回归方程特点

根据函数和回归方程的定义，可以看出二者虽然具有一定的差别，但是二者之间存在着很多相似点和联系。函数是一种理想的关系模型，而回归方程是一种非确定性的关系，存在随机变量。想要在解决函数问题时采用回归方程，就要使用回归分析法，这种方法主要是根据基础数据求值，最后得到回归方程。在进行回归分析中，首先要找到自变量和因变量，然后根据回归方程进行具体的分析。也就是说，在实际解决函数问题时，要根据问题中所给出的具体数据，画出散点图，然后区分自变量和因变量并且判断二者是否具有相关性。通过上文的分析，可以看出回归分析法具有以下几个特点，第一，回归方程中两个变量并不对等，分为自变量和因变量，具体要根据实际问题进行判断。第二，根据回归方程可以推导出因变量的估计值。第三，在不同关系的回归方程中，不能进行替换，方程之间相互独立。

二、实际例题详解

1.例题一

例：一家服装厂有很多设备，想要对设备进行管理，明确具体成本，因此将设备的使用年限设为x，并将设备需要支付的维修费用设为y，根据服装厂提供的资料，得到了如表1所示的X、Y数值：

表1 该服装厂的X、Y数值

根据表1中的具体数值能够确定在维修费用y和使用年限x之间有着一定的关系，要求出二者之间的线性回归方程，并且根据上述数据推导出，当该服装厂设备使用年限x=10时，对应的设备维修费是多少[1]。

解：首先求出计算线性回归方程所需要的具体函数，首先，维修费用y和使用年限x的平均数，然后，要计算出xi2和xiyi的总和等数值，最后，根据y=bx+a的方式得到b和a。

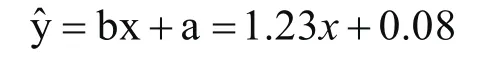
将x=10带入到该回归方程中，就可以估算出当该服装厂设备使用年限x=10时，对应的设备维修费y=12.38。在解答这一题目的过程中，首先通过具体的数据判断出维修费用y和使用年限x之间存在线性关系，在这的情况下，省略了检验这一步骤，如果无法确定二者关系时，就要进行检验工作，如果两个变量之间没有相关性关系，或者二者之间的关系并不显著，那么回归线性方程就是失去了作用，使用回归线性方程所得到的结果也不是最优解，因此可知，在使用回归方程时，必须要确定两个变量之间的关系，以此可以更加准确的解决具体问题，并且提升解题效率。

2.例题二

例：某农业科研所在对新品种大豆的发芽情况进行研究时发现，冬季昼夜温差大小和新品种大豆的发芽数之间有着一定的关系，为了明确二者之间的关系，该农业科研所进行了研究，并且记录了五天的数据，包括每一天的昼夜温差情况以及每天每100颗种子中的发芽数，得到了如下资料：

表2 科研所的具体数据

解题思路：在五组数据中，借助其中三组数据求出线性回归方程，在利用剩余两组进行检验，但是需要注意的是，在求解线性回归方程之前，必须要判断，用于检验的两组数据不是相邻数据的概率，以此得到线性回归方程的准确性较高。

解：首先要求出两组数据恰好是不相邻数据的概率，因为在五组数据中选出两种数据的情况一种有十种，每种结果的出现的概率相同，那么抽到相邻数据的情况有四种，因此两组数据恰好是不相邻数据的概率为3/5。继而分别求出发芽数y和温差x的平均数，分别为27和12，然后计算出xi2和xiyi的总和等数值，在此基础上就可以求出二者之间的线性方程如下：

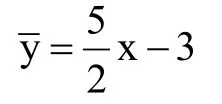
3.例题三

例：某工业车间为了提高生产产量，加快生产效率，展开加工试验，确定加工零件所需要花费的时间，继而确定工时定额，得到了十组试验数据，要求根据数据内容得到加工200个零件所需要花费的时间[2]。经过前两道例题的分析可知，首先要通过给出的具体数据进行分析，判断加工时间和零件数之间的关系，进而求出具体的回归线性方程，根据方程预测得出加工200个零件所需要花费的时间，需要的内容依旧为：y和x的平均数，然后计算出xi2和xiyi的总和等数值，最后根据y=bx+a，得到b和a的数值。

结语

综上所述，通过本文对高中数学函数与回归方程的详细研究，基于函数和回归方程的相关概念知识，对二者之间的关系和作用有了简单的了解，并且将回归方程应用到了函数数学例题中，并且对题目详细的计算，以此明确了回归分析法对函数数学题目的作用。未来，在遇到同类型的函数数学题目时，我们也可以通过建设对应回归方程的方式进行解答。但是，还需要进一步提高我们的理论知识记忆能力和实际运用能力。