剪叉式升降泳池驱动机构设计与仿真分析
2018-12-18王存堂徐敏舰谢方伟
王存堂,徐敏舰,谢方伟,张 兵
(江苏大学 机械工程学院,江苏 镇江 212013)
1 引言
升降泳池是一种能够实现池底在一定的深度范围内位置可调的泳池,使泳池能够满足各类对水深要求不同的人群以及适用于不同的应用场合,例如,公共泳池、水疗泳池和竞技泳池等。此外,在不需要使用泳池的时候,可以把池底升高至与地面平齐,作为表演舞台等[1]。升降泳池的核心机构是泳池升降平台的升降驱动机构,主要有链条式升降驱动机构、液压升降驱动机构、垂直丝杠升降驱动机构以及绳索式升降驱动机构[2]。目前,在日本、欧美等发达国家升降泳池技术已比较成熟[3],而在国内的相关技术还很少。因此,为填补国内的空白,设计一种水平丝杠剪叉式泳池升降平台。根据使用要求,该设计应满足以下使用条件:(1)池底高度能够自动灵活的任意调整;(2)池底应能承受较大的静载荷;(3)池底框架应该具备防腐蚀能力,初步设计的机械结构采用不锈钢材料。
2 结构原理与技术参数
2.1 升降平台基本性能参数设定
根据实际工况与产品适用性要求,将基本性能参数设置如下:
(1)台面规格:面积为 100m2;
(2)台面可调深度:1.8m;
(3)最大动载荷:80kg/m2;
(4)最大静载荷:300kg/m2;
(5)平均升降速度:0.2m/min。
2.2 升降平台总体结构设计
升降泳池的升降平台采用水平滑动丝杠传动剪叉支撑[4],如图1所示。其特点是设备结构紧凑、承载量大、运行平稳、传动精确、停位自锁可靠。驱动装置及台面采用模块化设计,设计时将台面分为两个模块,每个模块面积为50m2。每个模块的升降平台由驱动减速电机、传动轴、转向箱、传动丝杠、剪叉支撑机构、台面钢架等组成。其中每个单元的传动丝杠分为两组,每组由两根两端分别有左右旋螺纹的丝杠组成,并通过联轴器连接。左右旋螺纹上各有一个传动螺母,传动螺母又与支撑杆连接。考虑到泳池内的特殊工况,防止设备被腐蚀,池内的机构全部使用不锈钢材料,台面采用PVC面板铺设。
2.3 驱动原理
驱动减速电机通过传动轴、转向箱驱动丝杠旋转,进而通过丝杠螺母副将丝杠的旋转运动转换为移动,带动螺母及滑块沿着丝杠轴及导轨做左右移动,由于螺母的移动,驱动支撑杆摆动,从而实现泳池台面的升降。

图1 可升降游泳池水平丝杠传动剪叉升降平台示意图Fig.1 Schematic Diagram of the Horizontal Screw Drive of Movable-Pool-Floor
3 升降平台机构和力学分析
泳池升降平台的主平台主要由丝杠、承力导轨滑块、剪叉支撑杆、台面等构成。支撑杆两端分别与上下支撑座铰接,通过支撑杆的摆动实现台面的升降。主平台的结构参数及受力分析,如图2所示。

图2 泳池升降平台结构简图及受力分析Fig.2 The Analysis of Stress and Movable-Pool-Floor Structure Diagram
由图2可知:

式中:h—台面高度;h1—低位高度;h2—高位高度;θ1—起推角;θ2
—止推角;L—支撑杆长度(各支撑杆长度相等;)
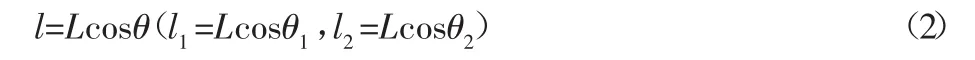
式中:l—支撑杆上下铰点水平距离;l1—台面低位时上下铰点的
水平距离;l2—台面高位时上下铰点的水平距离。

式中:H—升降行程。

单元主台面共有四组剪叉支撑杆,每组承载W/4,则每根支撑杆承载为W/8。支撑杆受力分析[5],如图3所示。
由受力分析可以得出升降载荷W与丝杆推力F推的关系为:

式中:F推—丝杠推力;W—升降载荷;θ—支撑杆与水平面的夹角。

图3 支撑杆受力分析Fig.3 Force Analysis of Support Rod
4 升降平台关键参数分析与确定
4.1 升降平台关键参数(夹角等)对丝杠推力的影响
根据产品性能参数设定,求得单元动载荷F动为39.2kN,单元静载荷F静为147kN。升降载荷W取动态载荷,即W=F动=39.2kN。根据式(5),利用MATLAB软件编写相应程序,运行后可以得到丝杠推力F推与丝杠与支撑杆间的夹角θ的关系曲线,如图4所示。

图4 丝杠推力F推与夹角θ的关系曲线Fig.4 Curve of Screw Thrust F推and Angleθ
由图4可知:随着夹角θ的增加,所需丝杠推力F推非线性减小,开始减小较快,然后变化趋于平缓。当θ为(0~15)°时,减小较快;当θ为(15~90)°时,减小较慢。因此,设计丝杆与支撑杆起始位置关系时,从受力方面考虑,应在安装空间允许的条件下,尽可能取较大的起始推角θ1值,降低起始推力。但是,从实际工况考虑,过大的起推角θ1对丝杠推力F推的影响并不显著,反而会造成空间的浪费。综合考虑,起推角θ1的值宜选在15°左右。
4.2 升降平台关键参数(夹角、杆长等)对升降高度的影响
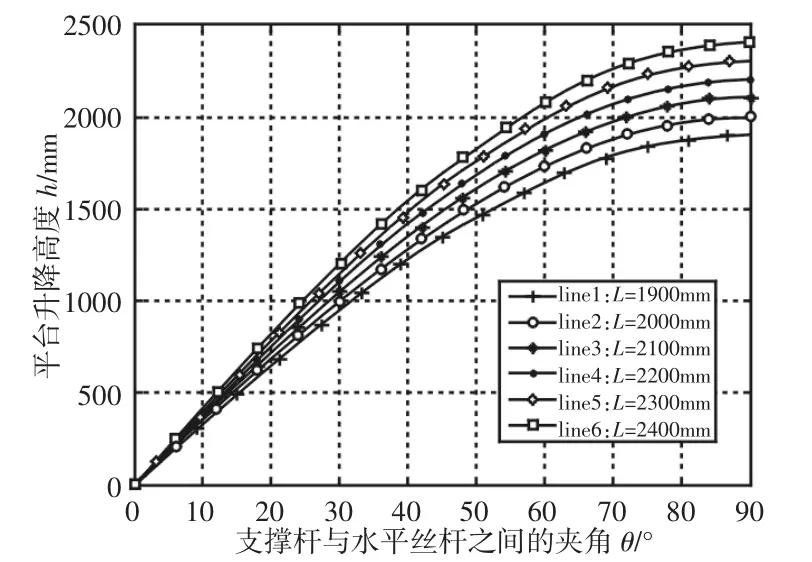
图5 平台升降高度h与夹角θ的关系曲线Fig.5 Curves of Platform Lifting Height h and Angleθ
根据实际工况,要求1800mm<L<2500mm-b/2,取b=100mm,可得 1800mm<L<2450mm。根据式(1)利用 MATLAB 软件编写相应程序,运行程序可得在杆长L取不同值时升降高度随夹角θ变化的关系曲线,如图5所示。
由图5可知:(1)在支撑杆杆长L确定时,升降高度随夹角θ的增大呈非线性增大,且开始增大较快,然后变化趋于平缓;(2)在夹角θ确定时,支撑杆杆长L越长,平台高度越高。根据实际工况,考虑到经济因素以及泳池池深的限制,平台升降高度不宜过大,因此支撑杆杆长L值的选取不宜过大。
4.3 升降平台关键参数(起推角、杆长等)对止推角的影响

根据式(6)利用MATLAB软件编写相应程序,运行程序可得杆长L取不同值时,止推角θ2与起推角θ1的关系曲线,如图6所示。
由式(3),可推得止推角θ2与起推角θ1的关系:

图6 止推角θ2与起推角θ1的关系曲线Fig.6 Relation Curve Between Thrust Angle θ2 and Lifting Angle θ1
由图6可知:(1)在支撑杆杆长L确定时,止推角θ2随起推角θ1的增大呈非线性增大,且开始增大较慢,然后不断加快;(2)在起推角θ1取相同值时,杆长L取值越大,止推角θ2越小,且在所选杆长范围内,止推角θ2的值均大于45°。
综合分析:根据实际工况以及结构特性,止推角θ2不宜过大,故起推角θ1的取值也不宜过大,且起推角θ1必须小于15°,同时杆长L的取值也不宜过小。
4.4 升降平台关键参数(起推角、杆长等)对功率的影响
由上文可知,升降平台是电机带动水平丝杠旋转推动支撑杆实现平台升降的,因此设计时应尽可能减小电机功率,节约能源成本。由于升降行程H和平均升降速度已设定,可计算得,升降平台单程升降时间T=9min=540s。设定丝杠推动支撑杆下端为匀速运动,速度为Vx,功率为:

式中:P—电机功率;Vx—支撑杆下支座水平速度。
结合图4可得,最大功率Pmax出现在起推角θ1处,由式(4)、式(5)、式(6)、式(7)整理,可得:

式中:Pmax—电机最大功率;T—升降平台升降时间。
根据式(8),利用MATLAB软件编写相应程序,可得不同杆长L下,最大功率Pmax随起推角θ1的变化规律曲线,如图7所示。

图7 最大功率P max与起推角θ1的关系曲线Fig.7 Curves of Maximum Power P max and Push Angleθ1
由图7可知:在四种杆长L下,最大功率Pmax在一定角度范围内呈先非线性减小,然后非线性增大,最后急速衰减的趋势。对比图6分析结果,急速衰减阶段不符合整体结构要求;故杆长L=2100mm时,起推角θ1=7.5°时,最大功率Pmax有最小值约为121W;杆长L=2200mm时,起推角θ1=9.5°时,最大功率Pmax有最小值约为96W;杆长L=2300mm时,起推角θ1=11°时,最大功率Pmax有最小值约为81W;杆长L=2400mm时,起推角θ1=12.5°时,最大功率Pmax有最小值约为71W。综合分析,杆长L取2300mm与2400mm时,可得到相对较小的最大功率。
4.5 升降平台关键参数对比分析
根据以上分析,利用MATLAB软件分析提取升降平台参数L、θ1、θ2、h1、h2、F推、Pmax值,筛选整理得对照表,如表 1 所示。
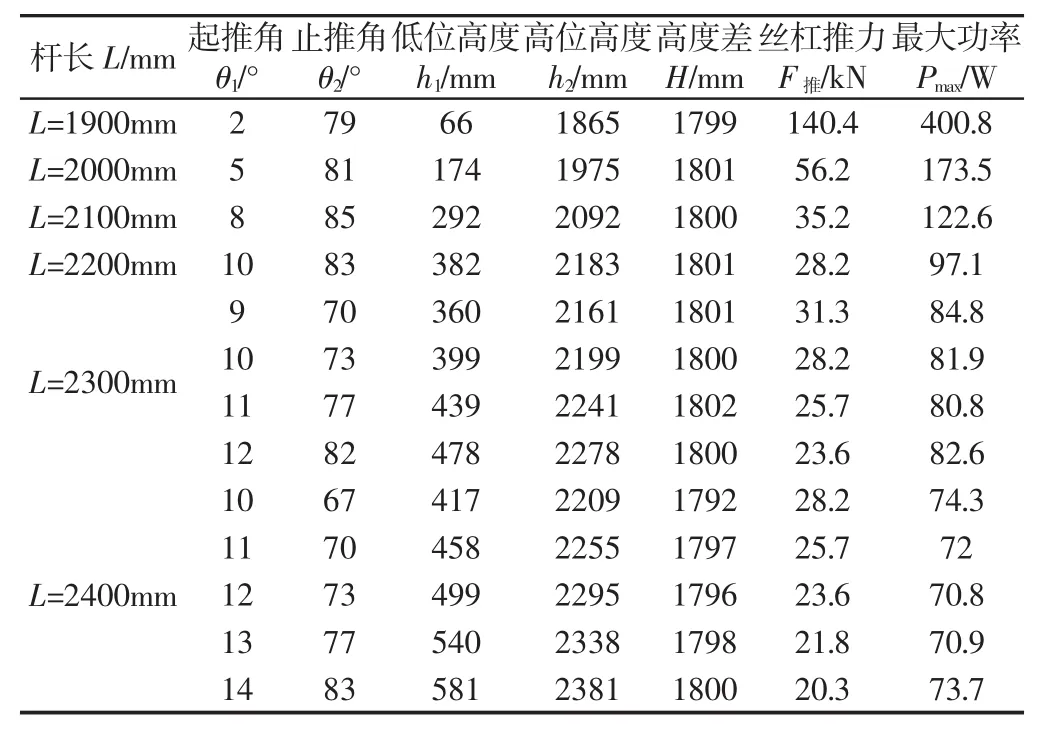
表1 升降平台结构、力学参数对照表Tab.1 Comparison of the Structure and Mechanical Parameters of Movable-Pool-Floor
从表1可得出:当杆长L=1900mm和L=2000mm时,满足实际工况的起推角θ1过小,导致丝杠推力F推过大,且对应的止推角θ2与最大功率Pmax过大,因此不宜选取;当杆长L=2100mm和L=2200mm时,满足实际工况的止推角θ2、最大功率Pmax过大,因此不宜选取;当杆长 L=2400mm,起推角 θ1=12°,θ1=13°和 θ1=14°时,止推角θ2和高位高度h2相对过大,起推角θ1=12°时,最大功率Pmax与高度差H偏差相对较大,综合分析,当L=2400mm时,起推角取θ1=11°最符合实际工况;当杆长 L=2300m,起推角 θ1=11°和 θ1=12°时,止推角θ2与高位高度h2相对过大,另外,起推角θ1=9°时与起推角θ1=10°时相比,起推角θ1=9°时,丝杠推力与最大功率都较大,综合分析,当L=2300mm时,起推角θ1=10°时更为合理。
当杆长L=2400mm,起推角θ1=11°时与杆长L=2300mm,起推角θ1=10°时相比,其高位高度过高,高度差偏差较大,故综合考虑优先选取 L=2300mm,θ1=10°,相应可得,θ2=73°,h1=399mm,h2=2199mm,l1=2265mm,l2=672.8mm。
5 升降平台的ADAMS运动学及动力学仿真
5.1 ADAMS模型的建立
ADAMS以计算多体系统动力学为基础,可对机械虚拟样机进行运动学和动力学分析[6]。运用ADAMS软件,对升降平台进行运动学和动力学仿真分析,可得出升降平台在运动过程中的运动规律和动力变化规律,并可得出台面处于最低位置时丝杠所受最大扭矩,为后续选电机提供依据。
在ADAMS/View中建立升降平台机构模型。由于利用ADAMS进行动力学仿真只需考虑零件的质量和质心,对零件外形不做要求,故为了提高仿真效率对模型进行适当简化,简化方法如下:(1)将台面框架简化为一薄面板;(2)将支撑杆用等长度的摇杆代替;(3)将螺母、螺母支座、撑杆下支座简化为一滑块;(4)将丝杠简化为旋转轴。
然后对简化几何模型施加约束、载荷和驱动:丝杠端与大地之间施加旋转副;丝杠轴与螺母之间施加螺旋副;支撑杆与撑杆上下支座之间施加螺旋副;台面与撑杆上支座之间施加固定副;在台面质心处施加39.2kN垂直向下的载荷;在丝杠轴左端施加旋转驱动[7],如图8所示。

图8 升降平台ADAMS模型Fig.8 ADAMS Model of Movable-Pool-Floor
5.2 升降平台仿真结果分析
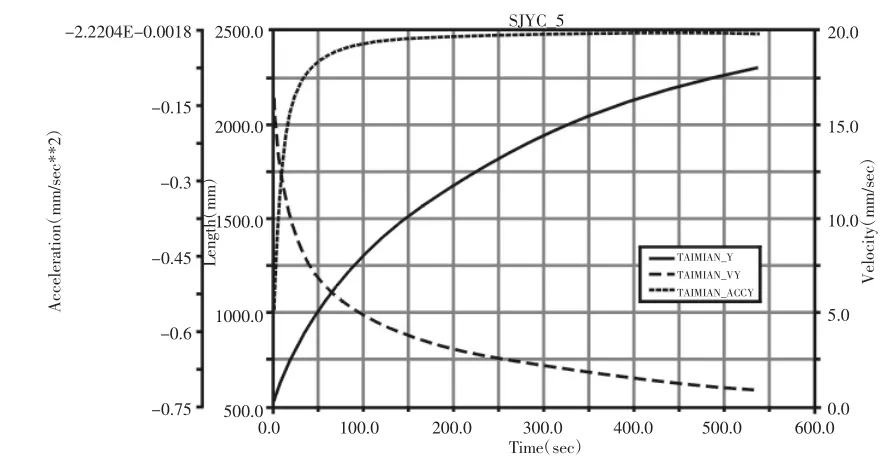
图9 台面位移、速度、加速度曲线Fig.9 Curves of Displacement,Velocity and Acceleration of the Table of Movable-Pool-Floor
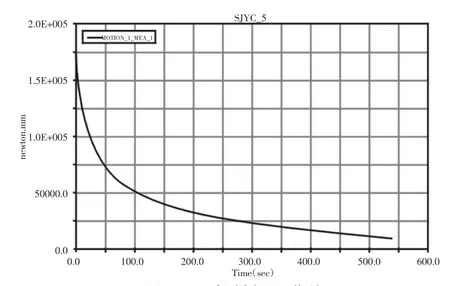
图10 丝杠轴扭矩曲线Fig.10 Curve of Screw Shaft Torque
升降平台由外围驱动电机带动丝杠转动,进而驱动剪叉机构实现台面升降,为了简化仿真模型将电机驱动转化为丝杠轴驱动。根据所设机构参数和基本性能参数要求,经过计算将丝杠轴旋转速度设为17.69r/min,仿真时间设为540s,仿真步数设为5000步。运行仿真后可得台面位移、速度、加速度曲线和丝杠扭矩曲线[8],如图9、图10所示。
由图9可知在起升阶段:(1)台面位移呈非线性增加,且开始增加较快后趋于平缓;(2)台面速度、加速度呈非线性减小,开始减小较快,100s后趋于平缓,降落阶段反之。由图10可知,丝杠扭矩非线性减小,且开始减小较快后趋于平缓。
6 结论
(1)设计了一种新型泳池升降平台,该升降平台采用水平滑动丝杠传动剪叉支撑机构驱动,研究得到其具有结构紧凑,运行平稳可靠,能够实现停位自锁等特点,满足升降泳池所需功能要求。
(2)通过对升降平台机构学和力学分析得到升降平台关键几何与物理参数的关系,并利用MATLAB仿真软件对升降平台的关键参数的关系进行仿真分析,研究得到最佳机构设计方案:杆长 L=2300mm,起推角 θ1=10°,止推角 θ2=73°,并为后续结构改进提供了优化方法。
(3)通过在ADAMS中建立升降平台物理模型,研究得到台面运动规律曲线和丝杠扭矩曲线,得到每根传动丝杠所受扭矩最大值约为Tmax=175N.m,为电机等部件选型以及控制策略研究提供理论依据。
