喷涂机器人运动控制和视觉补偿
2018-12-18李永杰邱继红
李永杰,臧 琛,邱继红
(1.乌海职业技术学院,内蒙古 乌兰察布 016000;2.内蒙古工业大学,内蒙古 呼和浩特 010051;3.中国科学院沈阳自动化研究所,辽宁 沈阳 110016)
1 引言
随着工业机器人的发展,六自由度喷涂机器人的产品已经趋于成熟,但相较于国外厂商,国内喷涂机器人产品的自主研发水平仍相对落后。有别于传统六轴机器人,国外厂商均采用斜交末端型机构,可以在避免内部管线打结的同时增强末端手腕的灵活性。
斜交末端机构在开发过程上主要难点在于逆运动学运算难度。六自由度机器人的逆运动学结果具有封闭解的充分条件在学术界已经达成共识,即其机构符合如下两个条件之一[1]:
(1)相邻的三个转动关节的轴线交于一点;
(2)相邻的三个转动关节的轴线之间相互平行。
喷涂机器人手腕不符合上述准则,其运动学不具有封闭逆解。作为喷涂机器人的底层核心算法,运动学逆解是必需的[2]。对喷涂机器人运动学问题的研究,学术界已经取得了一定成果。文献[3],对非正交手腕机构,利用方向余弦建立了各个关节运动学方程,并对其正、逆运动学进行了分析。文献[4]通过对奇异位置的处理和阻尼因子的调整,改善了阻尼最小二乘DLS算法,实现了实时运动学求解。文献[5]通过降低系统维度的方法,通过对运动学方程进行消元处理,将逆运动学求解的问题转变为一个一元十六次方程。
以六自由度喷涂机器人为实际背景,对其机械结构特征进行分析,通过D-H法建立了关节坐标系,通过数值迭代算法完成了逆运动学求解。算法将运动学问题的求解控制在毫秒级,确保了机器人逆解的实时性,并使用MATLAB验证了其有效性。最后部分阐述了视觉补偿的实现方法及其在喷涂机器人运动控制中的主要作用。
2 运动学建模
六自由度喷涂机器人的运动学建模就是建立各个关节与末端执行器之间的位姿映射关系。根据机器人的关节分布特性绘制的机器人各个局部坐标系分布图[6],如图1所示。

图1 固定在连杆上的坐标系分布图Fig.1 Structure of Coordinate System on Connecting Rod
2.1 机械臂运动学正解
喷涂机器人的运动学正解问题解决的通过电机转角,求得机械臂的末端位姿矩阵[6]。其最终变换矩阵为:

D-H的相关参数,如表1所示。

表1 机械臂的连杆D-H参数Tab.1 Mechanical Arm Connecting Rod D-H Parameters
根据以上这些参数可以得到各个关节之间的变换矩阵,令:
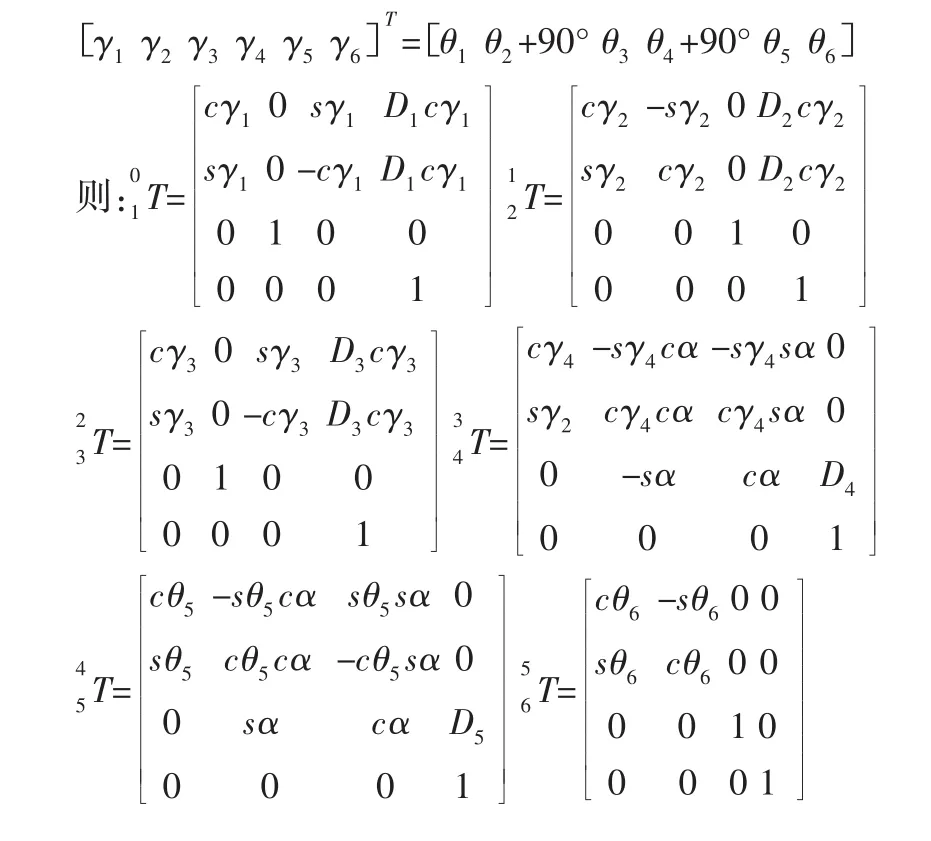
最后,得到六个连杆齐次变换矩阵的乘积:
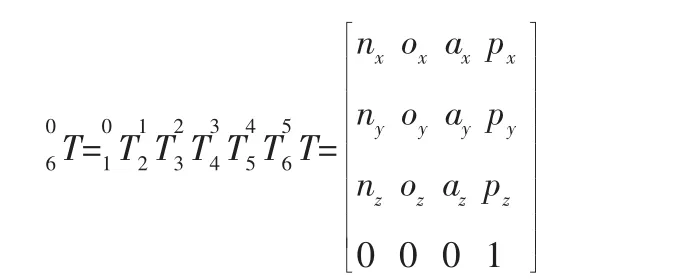
矩阵中各元素如下所示。

由上述方程组可以得到,机械臂末端位置仅与第一到第四关节的转角相关,第五、六关节转角仅影响末端姿态。为了验证求解的有效性,选取 θ1=0°;θ2=0°;θ3=0°;θ4=0°;θ5=0°;θ6=0°,可得到结果为:

根据关节坐标系分布图可知结论正确。
2.2 喷涂机器人运动学逆解
六自由度喷涂机器人运动学逆解问题是机械本体传动装置末端位姿来求解机械臂各关解转角的过程,机械臂的轨迹跟踪和示教作业功能均依赖于此过程逆解结果可根据关节运动范围和象限特征等舍弃不符合实际工况的结果[6]。
2.2.1 拟牛顿迭代法
式中:F(X(k))—第k次迭代中方程组对应的雅可比矩阵。对于雅可比矩阵不可逆的情况,其牛顿迭代格式可推广为:

式中:F(X(k))+—第k次迭代时雅可比矩阵的最小范数广义逆。
2.2.2 迭代过程推导
通过对运动学方程组的处理可得到六个方程。

由于o向量为单位正交向量可简化为四个方程。

其对应雅可比矩阵J∈R4×4如下。
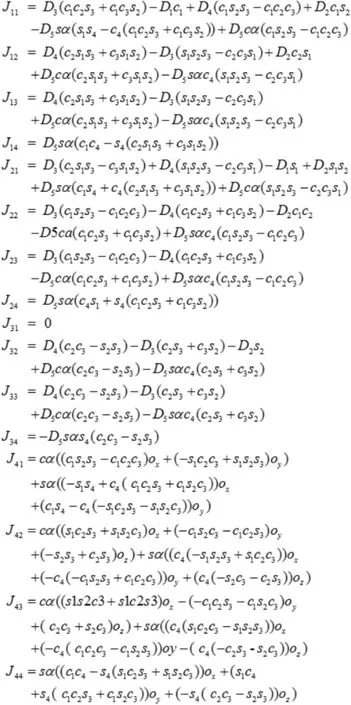
在通常情况下 F(X(k))+与 F(X(k))-1等价;当机器人末端轨迹穿过奇异位置时,雅可比矩阵不再可逆,采用上述迭代格式可适配极端情况。
3 逆解仿真
喷涂机器人在工作场景下通常需要往复运动于待喷洒工件表面附近,规划机器人末端轨迹为类正弦曲线,根据运动学逆解算法计算出各关节角度值,并将上面正弦曲线逆解求取出的一系列关节值代入正解运算公式中,求解出对应的一系列p向量,将逆解得到的p向量与初始位置p向量对比结果,如图2所示。
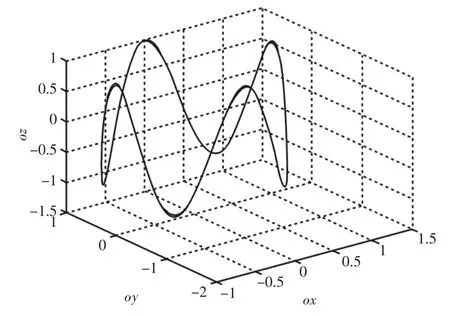
图2 运动学算法仿真验证Fig.2 Kinematics Algorithm Simulation Verification
图中其中一条曲线代表规划器所生成的位置,另一条曲线代表通过逆解后机器人末端的实际轨迹位置。从图中可看出两条曲线处于重合状态,足以满足实际机器人控制系统的精度要求。对于姿态的跟踪精度分别选取n、o、a三个向量进行比较。将计算后的姿态向量与规划器生成的姿态位置向量对比,如图3~图5所示。
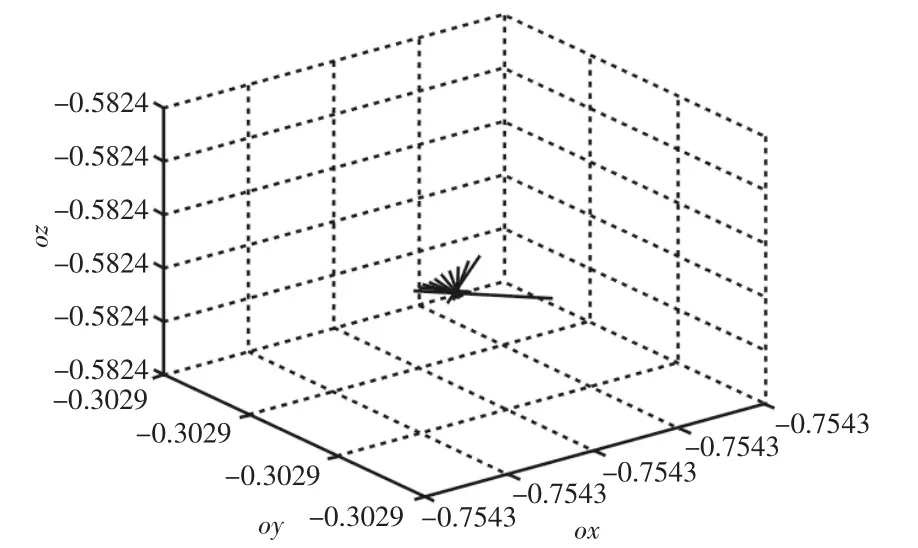
图3 姿态n仿真验证Fig.3 Simulation Verification of Posture Vector n

图4 姿态o仿真验证Fig.4 Simulation Verification of Posture Vector o
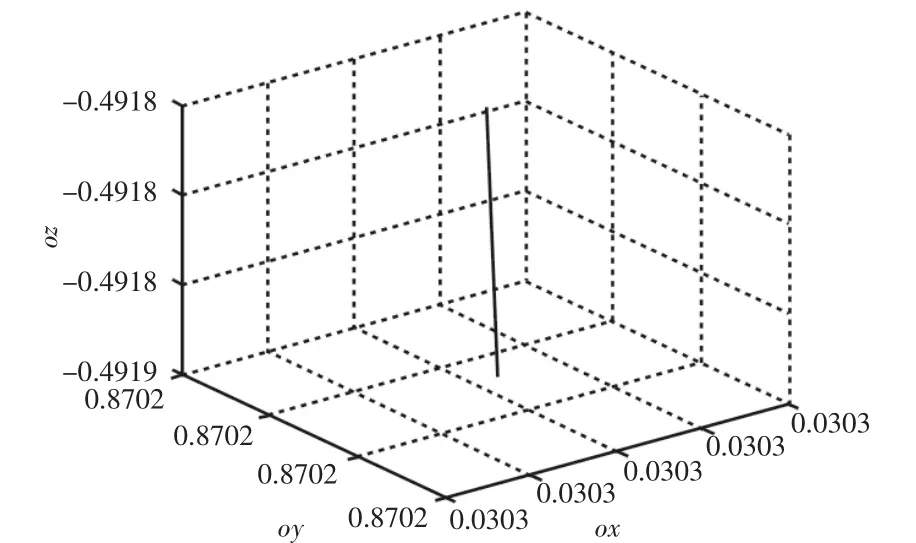
图5 姿态a仿真验证Fig.5 Simulation Verification of Posture Vector a
由图3、图4和图5易知,轨迹将部分完全覆盖,且在轨迹跟踪的全过程中,三个姿态向量的变化范围始终小于0.0001,完全符合实际机器人控制系统对精度的要求。喷涂机器人在实际工作过程中需要重复运动于工件表面上方,需规划类正弦曲线的轨迹用以覆盖喷洒区域。本次仿真中以类正弦曲线为例,分别对位置和姿态进行仿真跟踪,易见本算法对于位置和姿态的跟踪效果较好,对于每个向量的各个分量的跟踪误差均小于0.0001,满足了实际机器人的精度要求。
4 视觉补偿
针对喷涂机器人工作环境,首先利用工业相机对待涂装工件进行拍摄,获取工件数字图像信息,利用特征法对采集的图像信息进行分析,计算得出工件的质心,并与喷涂系统的坐标系进行整合换算得出工件的笛卡尔空间位置,最后引导喷涂机器人末端喷枪完成对工件表面的涂装工作。
4.1 摄像机标定
通过处理从摄像机采集到的数字图像,通过采集到工件的空间坐标信息,实现对工件的重构和识别[7]。将机器视觉应用于工业生产线必须首先进行对摄像机的标定操作。本系统的开发采用了张正友标定法,选择小孔成像为标定算法模型。根据图像点之间对应关系即可标定出摄像机内参数与外参数,此过程仅需拍摄2张相片[8]。本实验选用DALAS-GM1400工业相机,相机内参数如下:焦距:4.2864mm;精度:1.3020mm/pixel(长)、精度:0.9765 mm/pixel(宽);焦距:5mm;精度:1.116mm/pixel。摄像机标定结果,如图6所示。
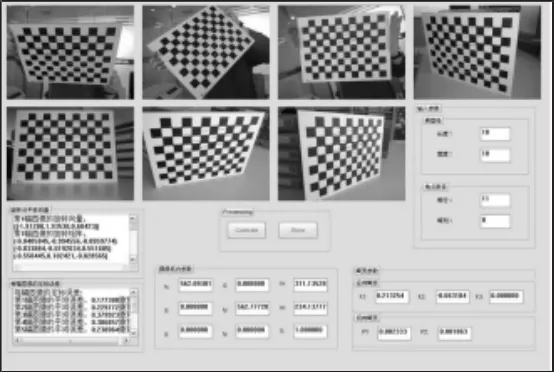
图6 摄像机标定实验结果Fig.6 The Experimental Results of Camera Calibration
本实验拍摄了7幅(1280×960)分辨率的高质量图像用以提高标定的精度[8],标定结果为:摄像机参数为fx=2241.1510,fy=2213.0495,u0=681.86539,v0=478.60121;摄像机畸变参数为 k1=0.053131,k2=0.944376,p1=0.001223,p2=0.001319。
本实验所采用的张正友标定法是一种介于传统标定法和自定标法之间的方法,其应用较为广泛。该方法选择棋盘格作为模板进行标定,实现的必要条件为需从不同角度拍摄2幅以上图片。为提高标定的精确度,本实验通过摄像机采集7个不同方向位置的数字图像,并根据图像与标定板之间的映射关系解算出摄像机内、外参数等信息,最后将参数输入到相关模型中。通过采集不同方向标定板中标定点的像素坐标,将其一一与世界坐标建立对应关系,实现将空间坐标系变换到图像坐标系,得到二维图像对应的三维空间信息,从而完成摄像机的标定。
4.2 高斯滤波
由于实际使用中存在相机镜头自身性能和工作环境的限制,工业相机拍摄所得的图像必然存在着不可消除的在噪声,进而使得图像存在模糊的情况,对图像进行滤波处理可使其特征更加明显[9]。本实验选择高斯滤波方法对采集结果进行滤波处理。其模板取值,如式(3)所示。

其中,σ决定模板的宽度,作用于的宽度与σ的取值正相关,即取较大的σ值可使利用此模板的窗口扩大。
4.3 特征识别
首先,将目标工件进行过图像预处理,其次,要针对静态工件的特征提取,最后,根据提取结果进行分类。特征提取旨在通过提取不同种类的工件的特征信息,作为识别工件的基本条件。特征匹配的方法中灰度直方图匹配和轮廓匹配应用较为广泛[8]。灰度直方图方法忽略所采集图像中的空间信息,而导致实际应用中定位精度较低[9]。
4.4 特征识别目标匹配
图像的边缘轮廓作为数字图像中最基本的特征之一,是图像中固有信息的一种重要表示,其不变性多种条件均适用,并且其具有对噪声不敏感的优秀特性[9]。轮廓匹配是基于图像中工件的边缘特征来识别图像。轮廓匹配方法能够在缩小数据计算量的基础上,尽可能地保留图像中的结构信息,忽略次要信息从而准确地对工件进行识别。工件特征提取结果,如图7所示。

图7 特征提取Fig.7 Feature Extractions
处理过程中,通常对数字图像矩阵整体进行研究,按照此方式对于图像的分析每次均需要扫描整个图像。这样会严重降低算法的实时性,识别的准确率也急剧下降。本实验通过对多个目标进行分块处理[10],不同目标块用 BlockN(i,j)表示。对目标图像采用此种处理方式,运算只需要针对单一目标块来进行,增强了算法的效率。分块处理后,多目标工件的特征识别的效果图,如图8所示。从图中易对待喷漆目标进行分类捕捉,然后喷成不同颜色。

图8 目标识别Fig.8 Target Recognition
对工件的目标位置进行定位,通常采用目标工件的质心作为图像信息的综合表征。
定义图像的(p+q)阶矩,如式(4)所示。
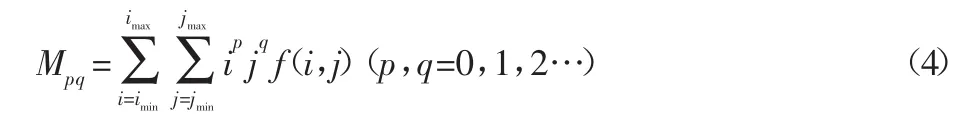
式中:f(i,j)—像素点的质量;
Mpq—图像的矩。
质心的位置可通过中心矩来求解,可得零阶矩M00、i轴惯性矩M01和j轴惯性矩M10。
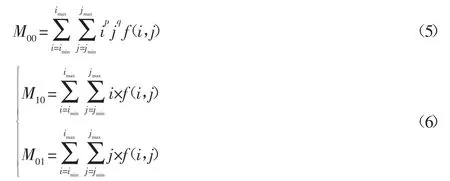
可得质心坐标为:(M10/M00,M01/M00)
5 总结
首先以斜交末端六自由度喷涂机器人的应用背景,通过DH方法建立了机械臂的关节坐标系,并构建了其运动学方程组。通过对运动学方程的分析,可得到以下规律:
(1)喷涂机器人末端位置仅与前四关节相关;
(2)根据机构特性可将逆解牛顿迭代格式中雅克比矩阵的阶数由6降至4,通过将姿态与位置分离的运算方式减小了运算量级;
(3)逆解迭代过程中雅克比矩阵的阶数与运算误差正相关,通过雅克比矩阵降阶,可减小计算误差,同时提高逆解的精度位数。
其次,从算法上实现喷涂机器人连续轨迹跟踪,并通过MATLAB仿真软件对算法进行验证,其正确性和精确性均得以确认,使得算法具有一定实际工业应用的价值和前景。
最后,在视觉系统中研究中,为减小计算开销、降低识别过程的错误率,使得基于视觉补偿的喷涂系统响应更加及时,工作流程更加可靠、稳定。
采用了如下方法:
(1)通过提取图像特征信息的方式对目标进行了识别和匹配;
(2)为增强算法的实时性并且减小识别过程中由于数据量巨大而带来的误差,采用对于多目标进行分块处理的方式。
综上所述,提出一种运动学算法和视觉补偿相结合的方法,使得喷涂机器人对于待涂装目标的捕捉更加智能、灵活,同时提高了机器人涂装过程的精确度。在精确控制机器人末端跟踪轨迹的同时,通过视觉补偿的辅助反馈信息,构建了待涂装工件与机器人末端的精准映射关系,运动算法和视觉识别的有效性分别通过仿真及实验得到验证。
