代理模型辅助进化算法在高维优化问题中的应用

田 杰 ，谭 瑛 ，孙超利 ，曾建潮

（1．太原科技大学 机械工程学院，山西 太原 030024；2．山东女子学院 数据科学与计算机学院，山东 济南 250300；3．太原科技大学 计算机科学与技术学院，山西 太原 030024；4．中北大学 计算机与控制工程学院，山西 太原 030051）

1 引言

目前，进化算法已经在复杂系统的设计中得到广泛应用[1]。通常这些问题都拥有大量的决策变量，因此被称为高维或大规模优化问题。而在这些复杂优化问题中，通常面临计算耗时问题，由于进化算法在每一代进化均需要大量的适应值计算，受限于算法对计算资源的要求，进化算法难以继续在复杂费时优化问题中发挥作用。因此，使用计算廉价的代理模型代替实际的计算费时的目标函数是进化算法用于解决复杂优化问题的一种有效策略。文献[2]通过基于多种近似模型的PSO算法对汽车吸能盒结构进行了抗撞性优化。文献[3]提出基于信赖域的采样空间更新策略，进而发展了一种基于信赖域的动态径向基函数代理模型优化策略。目前，常用的代理模型有响应面法，文献[4]，径向基法（RBF）以及支持向量机法（SVM）等。基于代理模型的进化算法中仍然存在一些重要的问题需要解决，如模型管理[5]，模型保真度的改善，如何利用更合适的加点规则来选取哪些解该被实际计算等。目前多种加点规则已用于模型管理，如期望改进（EI）、统计下限最小值准则（LCB）、改进概率最大值准则（PI）。文献[6]在20维问题上比较了以上三种常用规则的性能，得出EI及LCB性能略优。但由于GP模型给出的解之间的不确定性差异会随着维数的增大而迅速降低，因此也降低了现有加点规则的有效性。

2 多目标加点准则

从模型管理的角度出发，提出了一种新的多目标加点准则用于高维问题，将加点准则定义为一个两目标问题，将期望改进准则EI及统计下限最小值准则LCB作为两个目标，选取第一个Pareto面上的样本点进行实际计算，目的是为了可以从不同的加点准则中受益，提升算法性能，从而使加点规则能够适用于高维问题。在这里，多目标加点准则被定义为一个两目标的最小化问题，数学描述如下：

式中：S—决策空间，且 S：=［xmin，xmax］，xmin和 xmax分别用来定义决策空间的上下界；EI（x）—期望改进函数如公式所示，因期望改进函数本身是求期望改进最大化的函数，因此，我们将该函数前加负号，作为最小化函数处理；LCB（x）—统计下限最小值准则，如式（4）、式（5）所示：

式中：fmin—当前最优适应值、yˆ（x）、s（x）—由 GP 模型得出的关于解x的预测值及其不确定性度量值；ω—常数，在实验中，该数值为2。

3 MICGP-SLPSO算法

在所提出的MICGP-SLPSO中，社会学习微粒群算法（SLPSO）作为优化器产生候选解，用高斯过程（GP）模型对候选解进行预测，通过预测信息利用提出的多目标加点准则，选取个别候选解进行实际计算并更新GP模型。首先，初始种群用拉丁超立方体的方法生成，初始种群的适应值用实际函数进行计算，将初始个体的位置及适应值存入数据库，用于构建GP模型。下一步用公式和更新种群位置及速度，当需要实际计算的代数执行过后，进入使用GP代理模型的迭代，用实际计算过的个体信息构建GP模型，然后用GP模型给出种群中所有个体的适应值及其不确定性，然后根据这两个值用公式和计算每个个体的EI及LCB，利用多目标加点准则选择第一个Pareto面上的样本点重新用原函数进行实际计算，然后将实际计过的个体继续存入数据库，当数据库中的样本大于GP模型的训练样本个数n时，只从数据库中选n个最新的样本进行训练模型。

3.1 社会微粒群算法

社会学习粒子群优化算法（SLPSO）在高维问题上表现表现良好[7]，SL-PSO种群中的个体会按照它们的适应值排序，除了适应值最好的个体外，每个个体都将从适应值比自己好的个体中随机选择一个个体进行学习。如种群中第j个个体在第t+1代的进化公式如下：

式中：1≤j＜m，个体k是个体j随机选择的学习者，所以j＜k≤m，m是种群数m=100+D/10；xkd（t）—个体k的第d维元素（1≤d≤D，D是决策空间的维数）；—与个体j的适应值成反比的学习概率值；pj（t）—个体 j的随机数；r1，r2、r3—［0，1］区间内的随机数；（t）—当前种群在 d 维上的均值；

ε—影响因子。

3.2 构建GP模型

尽管GP模型已经在用于解决优化费时问题中得到广泛应用，但在高维费时问题的解决上却遇到了一些瓶颈，除了引言中所提到的GP模型的现有加点规则不能很好的适用于高维问题之外，随着训练样本的增加，构建GP模型的时间也会相对增加，而在高维问题上构建GP模型与低维问题相比，需要更多的训练样本，因此，高维问题上的GP模型构建变得更加耗时。因此，作者前期在如何构建GP模型能够满足精度的同时尽量提高效率上做了一定的研究与尝试，具体可参考文献[8]。基于以上分析，GP模型的具体构建方式描述如下：

创建含有 n 个样本（xi，yi），i=1，2，k，n 的数据库 DB，对任一候选解x的适应值y在GP模型中被看作为μ+ε（x）式中ε（x）服从分布 N（0，σ2）：

K 为矩阵，其中矩阵元素为 Kij=C（xi，xj），k（x）=［C（x，x1），…，C（x，xn）］T，X＝（x1，…，xn）为样本点的输入值，κ（x）=C（x，x）是x自身的协方差。C（·，·）为协方差函数，具体使用Matérn32函数作为协方差函数：

4 测试算例

为测试MICGP-SLPSO算法的有效性，选取了3个常用测试函数，具体函数详，如表1所示。函数公式参见文献[7]。分别针对这3个函数的30、50、100维，与目前性能较优的文献[4]及文献[9]算法进行性能比较，每个算法独立运行20次后进行结果统计。

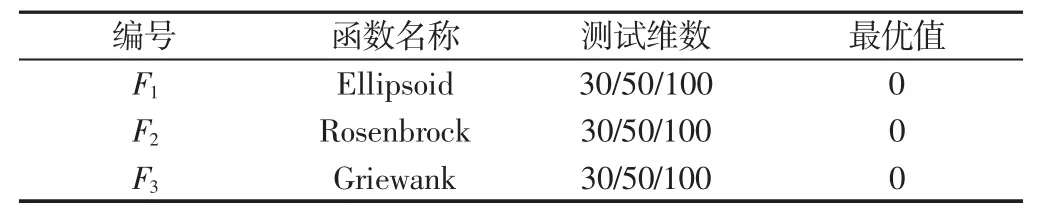
表1 三个标准测试函数Tab.1 Description of Three Benchmark Functions

与GPEME的比较结果，如表2所示。实际评价次数设定为1000次与文献[4]相同，由表2我们可以看出，提出的MIC-GPSLPSO在F1，F2和F3身上均获得了明显优于GPEME的结果，另外值得注意的是，在GPEME中使用的是LCB加点规则，因此，MIC-GPSLPSO常采用的将EI和LCB作为多目标设计的加点规则，要优于仅使用LCB的加点规则。

表2 MICGP-SLPSO与GPEME在30维问题上的结果比较Tab.2 Comparative Results Between GPEME and MICGP-SLPSOon 30D

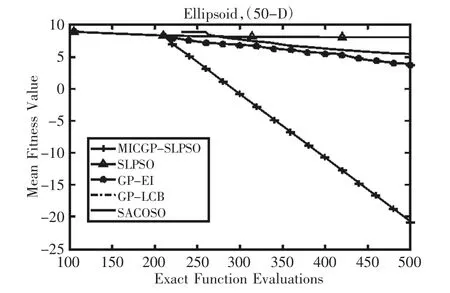
图1 50维F1迭代进化图Fig.1 The Convergence Trends for F1 on 50D

图2 50维F2迭代进化图Fig.2 The Convergence Trends for F2 on 50D

在高维问题上，选用性能优于GPEME，使用多模型且同时使用SLPSO和PSO产生候选解的SA-COSO[9]算法，以及GP-EI及GP-LCB这两个分别单独以EI规则及LCB规则来进行加点的算法在50及100维的问题上进行比较，实际计算次数减少到10D，D为候选解的维数。由图1～图6的比较结果可得，提出的MICGP-SLPSO无论在50维函数还是100维函数中，均取得了明显的优势，且在每一步都明显优于其他算法。

图3 50维F3迭代进化图Fig.3 The Convergence Trends for F3 on 50D

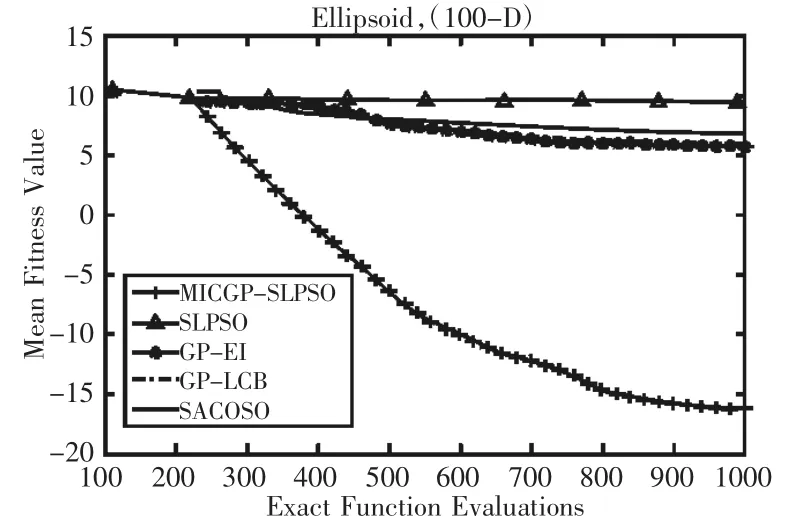
图4 100维F1迭代进化图Fig.4 The Convergence Trends for F1 on 100D

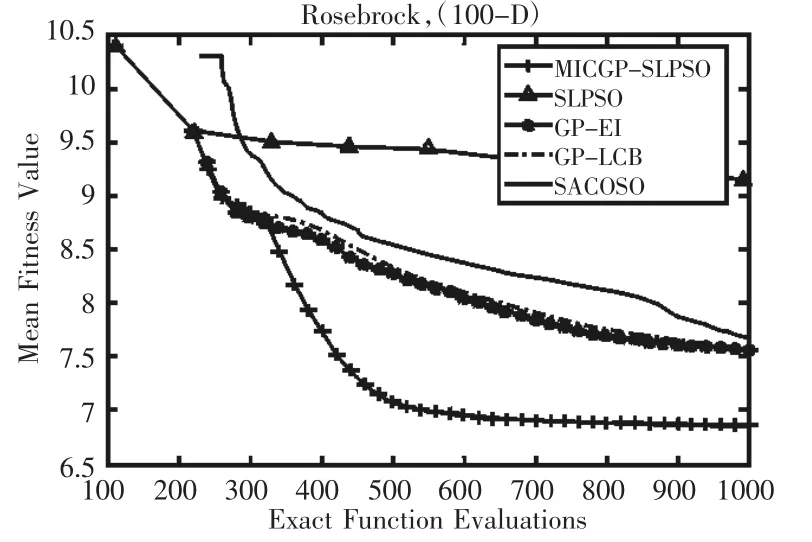
图5 100维F2迭代进化图Fig.5 The Convergence Trends for F2 on 100D

图6 100维F3迭代进化图Fig.6 The Convergence Trends for F3 on 100D

5 实例分析

5.1 实例的基本参数

选用的工程实例为一个d段阶梯轴端位移δ的最小化约束问题。该优化问题为一个30维的约束优化问题，其中，d=10，在阶梯轴的每一段，都需要优化三个参数：长（li）宽（bi）高（hi）。该阶梯轴的轴端受力为P=5×104N，材料性能参数为E=2×105N及σallow=350MPa，该问题的数学描述如下：

其中，σallow为所有阶梯轴的弯曲应力约束，AR=25为阶梯轴各截面的纵横比约束，Vmax=1.2×109为材料体积约束，Lmin=5为阶梯轴的长度约束。

5.2 实例结果比较

方法与优化方法在实例问题上的性能比较，如表3所示。针对该问题，在与现有文献算法GA，MPS结果（其优化结果来自文献[10]）比较的同时，增加了三个传统优化算法的结果比较，分别是内点法（IP），有效集法（AS）以及序列二次规划法（SQP）。从表3中我们可以看出，这里算法在更少的计算次数下取得了更优的结果。

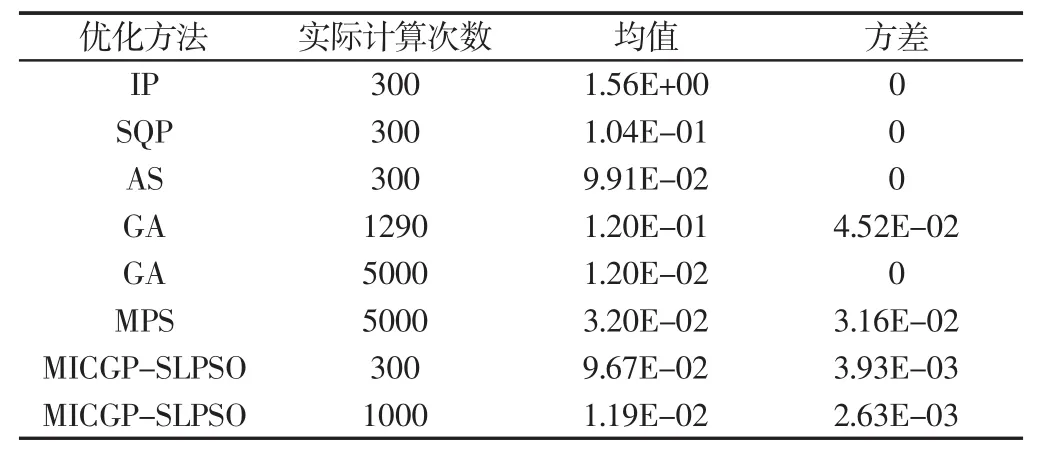
表3 方法与优化方法在实例问题上的性能比较Tab.3 Comparative Resultson 30D Cases

6 总结

设计了多目标加点规则，并将其应用到代理模型辅助的进化算法中，用于工程实践的复杂优化问题上，无论从测试函数还是实例问题的应用中，该方法都取得了较好的效果，且在高维问题上的优势更加明显。下一步可将所提的多目标加点规则辅助于其他进化算法并应用于CFD、FEA等其他更多复杂工程设计优化实例中，进一步检验MGP-SLPSO在工程问题中的实用性。