巡检机器人的双线圈磁力驱动方法
2018-12-18徐显金王云龙
徐显金 ,王云龙,严 宇,方 磊
(1.湖北工业大学 机械工程学院,湖北 武汉 430068;2.国网湖南省电力公司 带电作业中心,湖南 长沙 410100;3.武汉和越装备技术有限公司,湖北 武汉 430205)
1 引言
架空高压输电线路作业机器人主要包括巡检机器人、除冰机器人、绝缘子清扫机器人等以及其它智能检测和维护设备。近年来,高压巡检机器人成为研究热点,国内外的巡检机器人[1-10]大都采用轮臂式结构,通过行走轮与高压线之间的静摩擦力驱动巡检机器人移动,高压线结冰易导致巡检机器人打滑,严重影响巡检机器人的正常工作。为了解决该问题,文献[11]利用线圈在高压线周围受到的安培力作为驱动力的方法,解决了巡检机器人在高压线上易打滑的问题。然而,高压直流磁场强度往往是不确定的,且高压线路的坡度变化较大,导致文献[11]提供的驱动力大小不足,爬坡能力不强,负重载荷受到限制,在实际野外作业使用范围有限。
为提高磁力驱动巡检机器人的驱动力,在文献[11]的基础上,在不改变物理模型参数的情况下,提出一种双线圈结构的磁力驱动方法,将大、小两线圈相互交错嵌入磁芯材料中,在高压线电流、磁芯相对磁导率、线圈电流等模型参数大小相同的情况下,通过理论计算对比两种磁力驱动模型能提供的磁力驱动力,得出双线圈结构的磁力驱动模型能提供更大的安培力的结果。
2 磁力驱动实现原理
2.1 双线圈磁力驱动模型设计
文献[11]提出的磁力驱动实体模型,如图1所示。通过高压线周围产生磁场,软磁材料强化磁场,嵌入机体的载流线圈受安培力提供驱动力。文献[11]提供的理论驱动力大小为F合力:

式中:n—上机体线圈数,表示空气磁导率 u0(u0=4π×10-7H/m);ur—磁芯相对磁导率;I0—高压线电流;I1—线圈电流;R1—磁力驱动模型外径;R2—磁力驱动物理模型内径。

图1 磁力驱动实体模型Fig.1 Entity Model of Magnetic Driving
提出的双线圈磁力驱动实体模型,如图2所示。大、小线圈嵌入相互交错嵌入磁芯材料中。大、小两线圈受安培力牵引机器人移动。

图2 双线圈磁力驱动实体模型Fig.2 Entity Model of Magnetic Driving of Double Coils
2.2 磁力驱动原理分析
文献[11]提出的磁力驱动物理模型,如图3所示。水平方向,线圈受安培力合力沿着高压线方向;竖直方向,线圈受安培力相互抵消。

图3 磁力驱动物理模型Fig.3 Physical Model of Magnetic Driving
双线圈磁力驱动上机体线圈部分图,如图4所示。大、小线圈交错嵌入机体中,相互之间没交点。
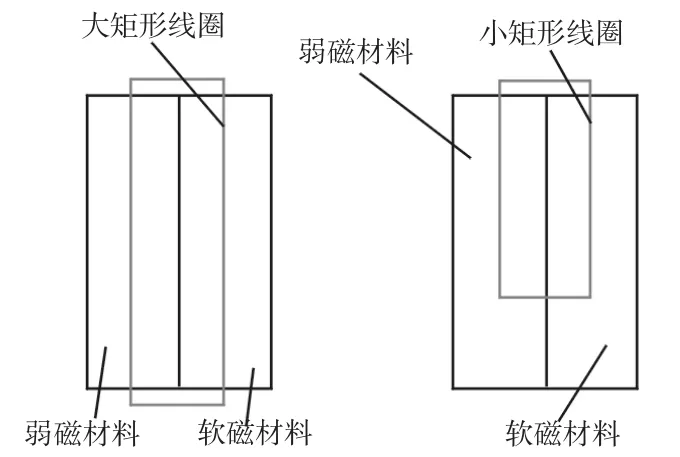
图4 上机体大、小线圈分布图Fig.4 Distribution of the Upper Body’s Coils
双线圈磁力驱动物理模型,如图5所示。大、小线圈所受的安培力驱动机器人移动。

图5 双线圈磁力驱动物理模型Fig.5 Physical Model of Magnetic Driving Double Coils
通电直导线在磁场中将受到安培力作用,根据安培定律,安培力大小F=BIL sinθ,由前述,载流线圈与高压输电线周围的环形磁感应线相互垂直,即θ=90°,故F=BIL。线圈长边上每处的磁场强度大小不等,故贯穿机体的大矩形线圈长边置于弱导磁材料中所受到的安培力为:

式中:R2、R1—双线圈磁力驱动物理模型的内径、外径;R3—小矩形线圈的一条边矩高压线中心的距离,如图5所示;I0—高压线电流;I1—载流线圈电流。
载流大矩形线圈另一长边置于软磁材料中,其强化后的磁感应强度B1为:

式中:ur—相对磁导率。
则贯穿机体的载流大矩形线圈长边在软磁材料中所受安培力F1为:

即单个大线圈与单个小线圈所受合力分别为F5、F6:

在不考虑磁场耦合及其它情况下,其双线圈磁力驱动系统受到的总推进力F:
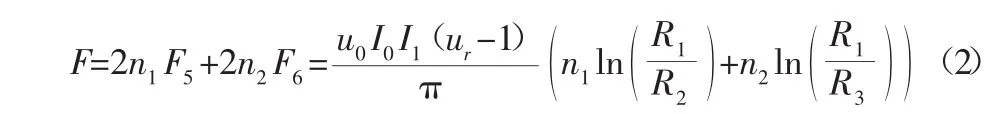
式中:n1、n2—上机体(或下机体)大矩形线圈、小矩形线圈的个数。
3 模型优化
线圈越多,受到的安培力驱动力越大。为了在双线圈驱动机体上布置更多线圈,采用双线圈交错布置的方法:大线圈和小线圈交替布置,线圈采用的裸线嵌入在双线圈驱动机体之中,线圈与线圈之间不能接触。线圈合理分布,如图6所示。图6中R0为高压线半径,为使高压线与机体避免接触摩擦,则满足R2>R0。

图6 线圈合理分布Fig.6 Reasonable Distribution of Coil
假设双线圈驱动系统内半径R2上相邻的大线圈与大线圈布置的夹角为ω,在ω内,小线圈零距离布置在双线圈驱动系统半径为R3上,如图7所示。

图7 小线圈零距离分布Fig.7 Zero Distance Distribution of Small Coil
双线圈驱动系统内半径R2上相邻大线圈a、b之间的圆心角为ω,在α到π-α间分布线圈,则相邻线圈之间的圆心角ω:

式中:k1—双线圈驱动系统上机体内半径R2上线圈的个数。
小线圈在半径为R3圆周上零距离缠绕分布时,且使小线圈的径向长度大于0,根据三角函数关系可得相邻小线圈截面圆心的圆心角η:

为使相邻大线圈之间至少有1个小线圈,且线圈与线圈之间有间隙,需满足不等式:

则双线圈驱动模型上机体布置的小矩形线圈个数必须小于或等于k3:
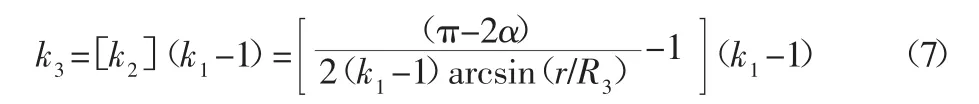

式中:r—线圈横截面半径。
双线圈磁力驱动系统在半径R3上,小线圈在缠绕时要保证非零距离布置,所以在角度ω内,双线圈磁力驱动系统上机体在半径R3上小线圈个数必须小于或等于k2:
其中,符号“[]”为取整符号。
4 仿真分析与驱动力理论计算
4.1 建立仿真物理模型
在高压电流I0=1000A的条件下设定物理模型参数,取内半径R2=0.048m,外驱动半径R1=0.092m;取R3为0.062m;取线圈横截面半径r为0.0015m;图6中取α=π/18;软磁材料为MnZn铁氧体,取其相对磁导率ur为1000;线圈电流取I1=10A;双线圈驱动机体厚度L为0.05m。
仿真物理模型,如图8所示。为便于仿真将实体模型中的缠绕线圈等效简化成单个独立的线圈。

图8 仿真模型图Fig.8 Physical Model Simulation
4.2 仿真分析
网格划分采用自由剖分三角形网格极端细化划分方式;选择稳态求解器直接求解方式进行模型求解计算。
基于以上的参数的设定。通过改变大线圈的个数n1与小线圈的个数n2,得到仿真安培力与原理分析时的安培力进行比较,验证原理的正确性。当上机体大线圈个数n1为4,小线圈个数n2为3和大线圈n1为5,小线圈n2为4时,分别得到的以下2个仿真截面图,如图9所示。分析以上仿真截面图,因为设定的高压线电流方向垂直截面向外,根据右手定则,高压线周围的磁场方向为顺时针环绕高压线,并且磁场强度随着远离高压线而变小,磁芯磁导率强于空气磁导率,磁芯中的磁场强于空气中的磁场,这些原理都在仿真截面图得以体现。验证了双线圈磁力驱动模型的正确性。上机体中的大线圈个数n1,对应仿真安培力F1(n1),如表1所示。力的大小单位是N。

图9 仿真截面图Fig.9 Sectional Charts of Model Simulation

表1 不同大线圈n1对应的仿真安培力F1(n1)Tab.1 Different Big Coils Corresponding to the Ampere Force of Simulation
通过以上的数据的特征,对仿真安培力F1(n1)与上机体大线圈数n1进行2次多项式拟合,得到曲线拟合图像,如图10所示。

图10 仿真安培力与上机体大线圈数拟合曲线图Fig.10 Fitting Curves of the Simulation Ampere Force and the Large Coil Number on the Upper Body
得到的拟合多项式为:
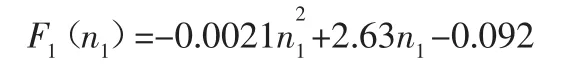
上机体中的小线圈个数n2,对应仿真磁力F2(n2),如表2所示。力的大小单位是N。

表2 不同小线圈n2对应仿真安培力F2(n2)Tab.2 Different Small Coils Corresponding to the Ampere Force of Simulation
通过以上的数据的特征,对仿真安培力F2(n2)与上机体大线圈数n2进行2次多项式拟合,得到曲线拟合图像,如图11所示。

图11 仿真安培力F2(n2)与上机体大线圈数n2拟合曲线图Fig.11 Fitting Curves of the Simulation Ampere Force and the Large Coil Number on the Upper Body
得到的拟合多项式为:

假设上机体大线圈数n1为15、小线圈n2为14,带入(8)式可得:
F(15,14)=57.8N
根据式(2),计算出来的理论安培力F:F=58.5N
通过比较以上计算出仿真安培力与理论安培力,仿真安培力与理论安培力大小相差很小,验证了2次项拟合的正确性,同时也验证了双线圈物理模型和理论原理的正确性。
4.3 比较理论安培力
基于以上物理模型参数的设定,通过控制大线圈与文献[11]的线圈数相等,通过改变小线圈数进行比较。
文献[11]取上机体线圈数n为30,根据式(1),计算出的机体所受的安培力合力F合力:
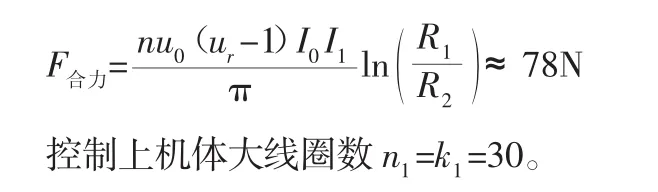
将k1=30,R3=0.065m,r=0.0015m 以上参数代入式(6)得 k3:
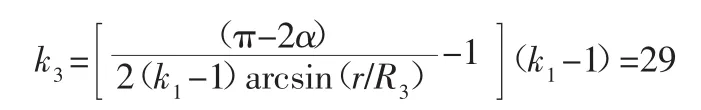
即上机体小线圈数最多可布置29个。取上机体小线圈数n2=29,将 n1,n2,I0,I1,ur,u0,R1,R2,R3的取值代入公式(2)得机体最大安培力合力F:

双线圈的磁力驱动比文献[11]提供的安培力最大可提高约。相当于在原有基础上提高了接近的安培力。对于巡检机器人作业在因坡度过大的路段及负载限制有很大改善。
5 结论
机体所受理论安培力大小与仿真计算结果相差很小,证明了双线圈的磁力驱动模型的正确性;由于磁场耦合的作用,得到到理论安培力与仿真安培力大小不相等,同时仿真采用迭代计算方法与Matlab曲线拟合所造成的误差,也影响仿真安培力的大小;双线圈磁力驱动机器人可根据实际作业情况来布置布置双线圈的个数和改变线圈电流大小来满足机器人所需要的安培力驱动;可以通过控制线圈电流方向实现机器人的移动方向。
