六足爬壁机器人的运动学建模与仿真

邓超锋，魏 武，侯荣波，余俊侠

（华南理工大学 自动化科学与工程学院，广东 广州 510641）

1 引言

六足机器人因机构简单且灵活、承载能力强及稳定性好[1]，且具有良好的运动灵活性和环境适应性等优点，同时其肢体冗余的结构特点保证了机器人能够完成多种工作，在核工业、建筑、交通、石化和消防等领域有较好的应用前景[2-4]。具有很重要的研究意义和实用价值。一直是国内外的足式机器人研究的重点。

需要通过控制六足机器人而使其完成特定的任务，其中最为普遍的一个方面是对其运动的控制。可以把六足机器人看作是由六条腿组成的并联机构，而每条腿是由多个连杆经关节构成。因六足步行机器人的多链结构、时变的运动拓扑，而且还具有冗余驱动系统，其运动学较轮式移动机器人运动学要复杂的多[5]。控制机器人的运动就是控制机器人各连杆及各关节之间的相对位置、速度及力。所以，六足机器人运动学模型为完成对六足机器人运动控制的基础。

机器人运动学分析包括正运动学和逆运动学分析。正运动学分析是指根据给定的机器人各关节变量来求解出机器人末端执行机构的位置与姿态；逆运动学是指根据给定的机器人末端执行机构的位置与姿态，反求解出机器人各关节变量[6]。如为了使得服务机器人手臂正确运动，甘弋等建立了服务机器人的拟人臂和底盘的运动学模型[7]。文献[8]建立了单臂SCARA真空手的运动学模型。

最常用的模块化机器人运动学建模方法是D-H法，但传统的D-H参数法需要在每个关节上建立坐标系后才能对机器人运动学求解，并且根据各关节的运动方式不同坐标系的姿态会有所区别，所以建立坐标系的过程较为复杂。旋量理论把刚体在空间中的任何运动均看成刚体绕空中的某一特定轴线的转动和沿该轴线方向平移的复合运动[9]，其中这一特定轴线为旋量轴，同时称对某旋量轴进行旋转和平移的运动称为旋量运动。基于旋量方法的运动学建模仅根据各关节轴线的位姿来描述执行器端的位置和姿态的，较D-H法更加直观、简洁。因此，只需要在每个关节处找出关节运动副的旋转轴线或者运动方向轴线，求解过程更加简洁。对模块化机器人机构不确定的特性能具有更好地适应性。近年来，旋量理论在机器人领域，包括机器人运动学、动力学等方面都得到了较广泛的应用[10-11]。

采用旋量的指数积对六足爬壁机器人运动学模型进行了建模。并求解其逆运动学问题，并结合MATLAB和ADMAS仿真分析所建立的模型的准确性。

2 六足爬壁机器人机体结构模型

机器人的机体结构模型，如图1所示。其主体部分为正六边形结构。共有六条腿，均匀分布在正六边形的六个方位。每条腿共有五个转动关节，分别为髋关节、膝关节、踝关节、足1关节、足2关节，末端位置由一个万向球铰连接一个真空吸盘。各关节转动方向与角度范围，如表1所示。

这种结构的机器人具有较高的运动灵活性，在进行方向调整时不需要旋转机体，只需要调整腿部顺序。机器人整体自由度较高，可以变换多种步态使机器人适应不同的环境。

图1 六足爬壁机器人机体模型Fig.1 The Body Model of Hexapod Wall-Climbing Robot

表1 各关节转动方向与角度范围Tab.1 The Direction of Rotation and Angle Range of the Joints

3 基于旋量理论的机器人运动学建模

根据旋量理论建立六足爬壁机器人单腿模型，如图2所示。以机器人正六边形机体中心为原点，x轴指向髋关节，z轴垂直于六边形指向上方，y轴由右手定则确定建立基础坐标系｛S｝。在末端执行器吸盘上建立物体坐标系｛T｝。ωi和qi分别为各关节旋量轴的单位矢量和其上一点，Li为各连杆长度。取姿态为腿部初始状态，如图2所示。

图2 机器人单腿模型Fig.2 Robot Single Leg Model

当机器人腿部处于初始状态时，根据空间坐标系的位姿描述，可知以｛S｝为基础坐标系，物体坐标系｛T｝的位姿描述为：

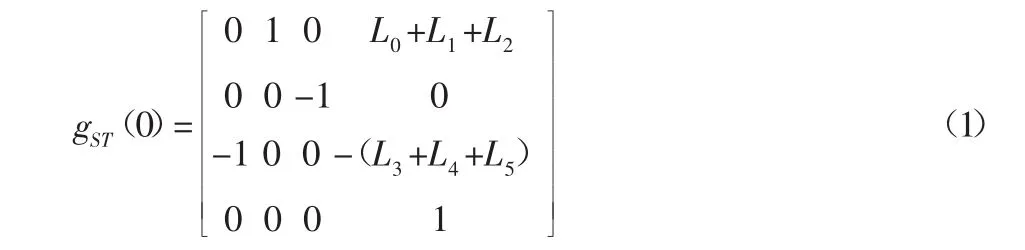
机器人单腿5个旋转关节的旋转轴单位矢量分别为：

对于纯转动关节，当ω≠0的时候，关节转动绕旋转轴ξˆ转动角θ时的旋量指数积：

继而可求解出机器人单腿正运动学模型如下：

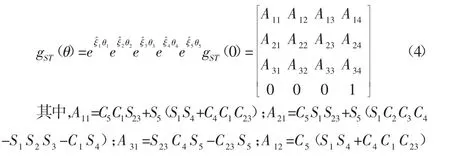
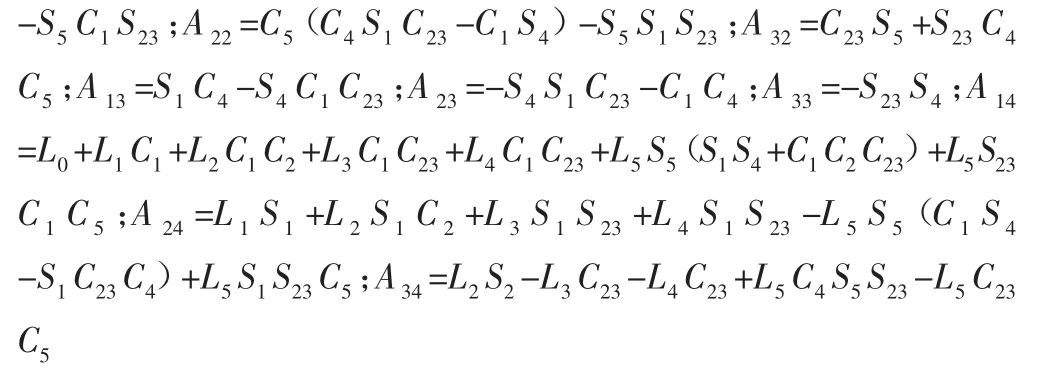
4 求解六足机器人逆运动学模型

六足爬壁机器人设计中足1关节与万向球铰功能均为提高机器人适应不平整壁面的能力，为了简化逆运动学模型，提高机器人运算效率，假设机器人足1关节无法旋转，即等式θ4==0。

将θ4=0，代入正运动学模型，得到简化后的机器人正运动学模型，即：

说明：与上文类似，为简化书写，用 Ci表示 cosθi，Si表示 sinθi，Cij表示 cos（θi+θj），Sij表示 sin（θi+θj），Cijk表示 cos（θi+θj+θk），Sijk表示 sin（θi+θj+θk）。

多足机器人单腿末端吸盘在机体平台参考坐标系｛O0｝下的坐标为pH=（pxpypz）T，螺旋旋转轴zHS5在参考坐标系下表示为 zH=（nxnynz）T，因此可得方程组如下：

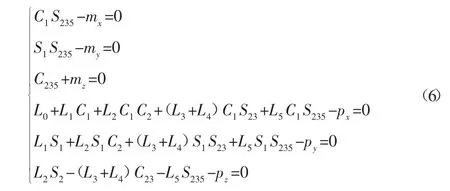
方程组中有6个等式，4个未知数，依据该方程组以及表1所规定的机器人各关节相对转动角度范围可以分析求取各关节旋转角度如下：

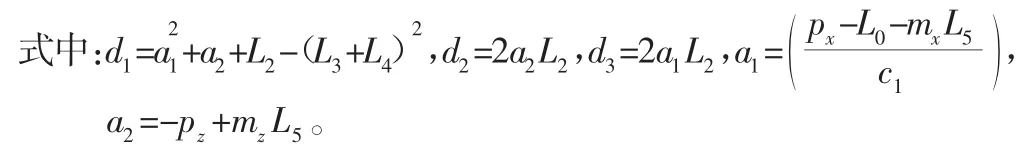
到此已经求解出除足1关节外，多足爬壁机器人单腿所有关节的相对转动角度，即建立了多足爬壁机器人单腿逆运动学模型。

5 机器人逆运动学仿真验证

根据建立的机器人逆运动学模型可以求解出期望位姿下各关节相对转动角度。为验证逆运动学分析的正确性，需要对建立的运动学模型进行仿真验证。

ADMAS是集建模、求解、可视化技术于一体的虚拟样机软件，它可以产生复杂机械系统的虚拟样机，真实地仿真其运动过程，且其求解器采用多刚体系统动力学理论中的拉格朗日方程方法，建立系统动力学方程，对虚拟机机械系统进行静力学，运动学和动力学分析，故采用ADMAS作为仿真软件。

为了仿真机器人运动，首先设计多足机器人的行走步态，旋转步态是多足机器人的常见步态，在机器人运动过程中遇到障碍物，或行走在复杂地面情况下，常常需要用到旋转步态来调整落足点的位置，且旋转步态较常见的三角步态、四角步态复杂。为更好地说明运动模型的适用性，在ADMAS上对多足机器人的旋转步态进行仿真，并对其逆运动学问题进行求解。同时，因MATLAB具有强大的运算能力，在MATLAB软件下根据建立的逆运动学模型求解机器人末端执行器按预定轨迹运动时各关节转动角度。通过对比ADMAS自动求解和MATLAB求解出的各关节转动角度随时间变化的曲线，并分析MATLAB求解出的各变量与虚拟样机相对应的变量之间的误差来验证建立的机器人运动学模型的准确性和适用性。

本次仿真验证设定多足机器人完成原地旋转步态运动，同时为了减少对吸盘的磨损，设定多足机器人腿部末端吸盘始终与壁面平行。旋转步态由机体旋转和腿部摆动回复零位两阶段组成。在旋转阶段，多足机器人六条腿均为支撑腿，此时机器人与壁面可以看作并联机器人，机体旋转可以看作机器人腿部相对其旋转，由对称性可知，此时机器人各条腿相对应关节旋转角度相同；在回复零位阶段，多足机器人三条腿着地作为支撑腿，另外三条作为摆动腿，交替回复到初始状态。虚拟样机步态运动，如图3所示。

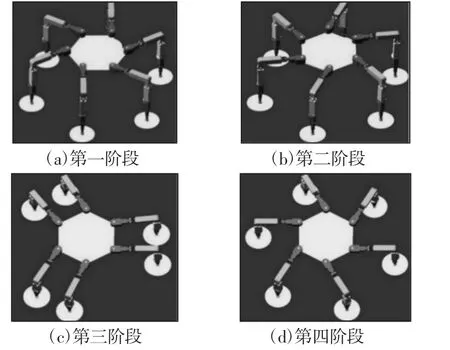
图3 虚拟样机旋转步态运动Fig.3 Rotational Gait Motion of Virtual Prototype

当虚拟样机完成设定的步态后，利用Adams仿真软件自动求解出各关节转动角度随时间的变化曲线。接着利用MATLAB软件求解机器人旋转步态中各关节理论上的转动角的随时间变化的曲线，并与Adams软件求解出的结果进行比对，如图4～图9所示。

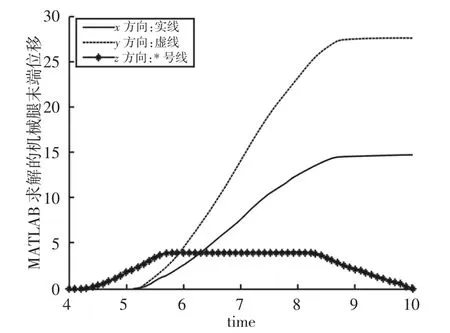
图4 虚拟样机中单腿末端位移Fig.4 Displacement of Single Leg End in Virtual Prototyping

图5 MATLAB中的单腿末端位移Fig.5 The End of the Single Leg Displacement in MATLAB

图6 MATLAB求出的理论各关节角度Fig.6 The Theoretical Angle of Each Joint Obtained by MATLAB

图7 虚拟样机仿真的各关节角度Fig.7 Joint Angles of Virtual Prototype Simulation

图8 单腿的各关节角度误差率Fig.8 The Angle of Each Leg Joint Error Rate

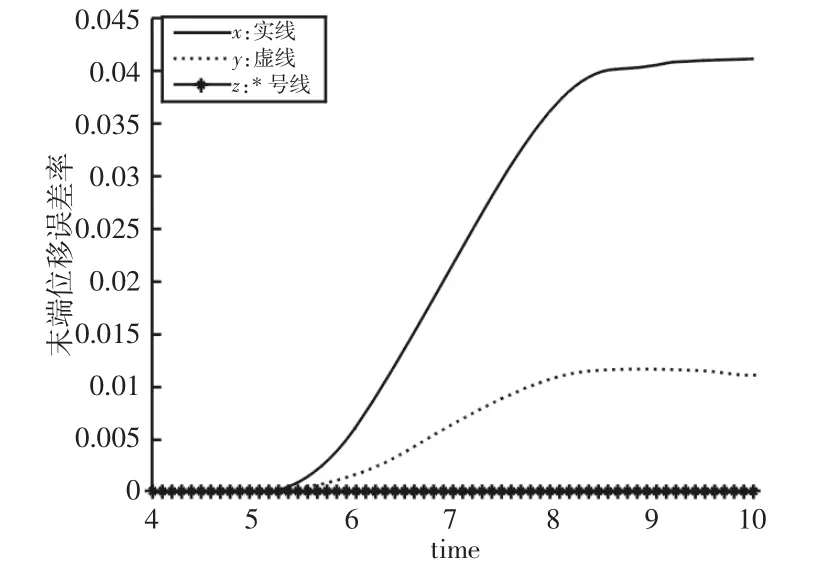
图9 单腿末端位移误差率Fig.9 The Error Rate of Displacement of the End of a Aingle Leg

通过对比分析以上几图可以看出，理论结果和仿真得到的结果基本一致，其中单腿各关节中角度误差率最大为4.4%，末端位移误差率最大为4.1%，误差较小。误差产生的原因主要包括两部分：第一是建立虚拟样机模型中存在一定的模型误差；第二是在积分、求导计算角度时会存在微小的算法误差。

6 结论

基于MATLAB求解的旋转步态下机器人末端的轨迹和腿的各关节角随时间的变化图，并与ADMAS仿真软件自动求解出来的多足机器人的各腿轨迹和各关节转动角度进行对比，得出以下结论：（1）通过旋量理论建立的多足机器人运动学模型可以准确性高，误差较小。（2）基于旋量理论建立的多足机器人的运动学模型可作为多足机器人研究的基础。