轨道梁动力行为对跨座式单轨车辆走行性能的影响

李小珍，葛延龙，晋智斌，朱艳



轨道梁动力行为对跨座式单轨车辆走行性能的影响

李小珍，葛延龙，晋智斌，朱艳

(西南交通大学土木工程学院，四川 成都 610031)

针对跨座式单轨车辆通过轨道梁桥时，轨道梁的振动与变形会对车辆走行性能产生影响，建立跨座式单轨车辆-轨道梁空间耦合振动模型，计算分析不同车速、载客量条件下轨道梁区段和路基区段的车桥动力响应，进而探究轨道梁动力行为对车辆动力响应的影响水平与规律。研究结果表明：标准形式PC轨道梁动力性能良好。轨道梁跨中竖向挠度的峰值与车速关系不明显，随载客量的提高显著增大；跨中横向位移的峰值随车速先增后减，受载客量影响较小。轨道梁跨中竖向加速度随车速先增大后趋于波动，跨中横向加速度随车速的提高呈上升趋势，且二者基本不受载客量影响。轨道梁的动力行为是影响车辆竖向振动加速度的主要因素，其单独引起的车体横向振动加速度占比约50%。强化对轨道梁竖向振动和横向变形的控制可有效提升车辆的走行性能。

跨座式单轨交通；轨道梁；载客量；动力响应；走行性能

轨道交通建设是关乎城市可持续发展的民生工程。跨座式单轨交通具备地形适应能力强、环保性能优越、建设周期短、造价低等多重优势，可有力保障城市客运系统的高效运转，是一种应用前景广阔的城市轨道交通形式[1]。跨座式单轨技术的日益完善和成熟，使其从纯粹的游乐设施发展成为一种公共交通工具，并在许多国家得以应用和发展。跨座式单轨车辆骑跨在轨道梁上方，依靠走行装置(如图1所示)沿轨道梁行驶，利用夹行在轨道梁两侧的导向轮与稳定轮来保障车辆行走的安全与平稳[2]。车辆在通过轨道梁桥时，会引起轨道梁结构的振动，而轨道梁的振动又会反过来影响车辆的振动，二者相互激发、相互影响，便是车桥系统的振动耦合问题[3]。跨座式单轨车辆振动的外部激励源包括轨道梁表面不平度、曲线段超高等，而影响车桥动力响应的因素主要有列车动力参数、运行车速与载客状态，轨道梁表面不平度及其动力参数等，这些要素将直接或间接地影响跨座式单轨交通的行车安全平稳与乘坐舒适性能。杜子学等[4]将转向架和车体均看作刚体，采用满载车辆以36 km/h速度通过最小半径为100 m的“S”型曲线轨道梁桥时，对跨座式单轨车辆的运行安全性进行分析和评价。周小芳[5]基于Rayleigh法基本原理推导了轨道梁横向自振频率的简化计算公式。Chang等[6−7]现场实测了钢轨道梁的表面不平度样本，用于车桥动力响应分析。结果表明，空车状态下车辆振动响应最大，并提出轨道梁的横向位移来自轨道梁剪切中心与列车竖向荷载的偏心引起的扭转效应。马继兵 等[8−9]指出，线路光滑时车体振动主要由轨道梁的振动引起，线路的平整度对车体动力响应的影响较为显著；刘羽宇等[10−11]的研究表明，车速与表面不平度对轨道梁竖向挠度影响较小，对竖向加速度影响较为明显; 不同的表面不平度在车速大于40 km/h后对车体竖向加速度的影响较大。张凯[12]的研究表明，轨道梁和车体的横向振动响应随曲线半径的增大呈递减趋势，竖向振动响应受曲线半径的影响较小。乔志[13]探讨了跨座式单轨桥梁的基频限值，并对不同车速和梁高条件下轨道梁的动力系数进行计算分析，整理得出轨道梁跨中截面动力系数与基频比的线性拟合公式，为结构设计提供参考。

图1 单轨车辆走行系统

轨道梁作为跨座式单轨交通系统的承载结构和运行轨道，对车辆走行性能的影响成分主要体现在2个方面：一是表面不平度，另一个是轨道梁的动力行为。表面不平度对车体振动响应的影响已在上文叙述，而关于轨道梁动力行为对车辆走行性能影响的研究目前在跨座式单轨领域开展较少。张晓波[14]运用SIMPACK和ANSYS 软件进行车桥动力响应研究，探究桥梁刚度对高速列车走行性的影响规律。刘国[15]的研究表明，轨道梁横向和竖向刚度分别对跨座式单轨车辆横向和竖向乘坐舒适性影响很大。车辆运行时的振动水平决定了车辆的走行性能。为探究轨道梁动力行为对车辆振动响应的影响水平与规律，将上述2种要素分离开来，分别计算车辆在弹性轨道梁和在具备相同不平度的刚性路基区段运行时车体的振动响应，二者差值即为轨道梁动力行为单独引起车辆振动的动力响应。突出轨道梁动力行为对车辆走行性能的影响，可为轨道梁结构设计提供参考。

1 车桥耦合振动理论与模型

1.1 车辆动力模型

采用空间车辆振动模型，可以较为真实全面地描述车辆振动状态。将每节车辆的车体和前、后转向架均视为对称刚体，每个刚体考虑伸缩、沉浮、点头、横摆、侧滚和摇头6个自由度，即每节车辆共计考虑18个自由度。跨座式单轨车辆空间动力模型的侧视图如图2所示。

假定单轨车辆沿硬性轨道路面等速前进，车轮和轨道梁之间始终保持密贴；走行装置结构对称，将橡胶车轮与中央悬挂装置视为并联的线性弹簧-粘性阻尼元件，且各轮胎模型仅考虑径向刚度和阻尼，忽略荷载和胎压变化对车轮动力参数的影响。

依据车辆系统动力学理论，采用虚功原理推导出单轨车辆运动微分方程(如式1所示)，进而求解车辆动力响应。

通过车辆行驶时转向架的运动位移来表示轮胎变形量，将其输入相应的轮胎模型中获得轮胎力与力矩，分别作用于转向架与轨道梁上。

分析中采用跨座式单轨列车为6辆编组(Mc1+ M2+M4+M5+M3+Mc2)，计算工况中载客量包括AW0(空车)、AW2(定员、6人/m2)和AW3(超员、9人/m2)3种不同状态[2]，设计车速为5~80 km/h。车辆动力性能对车桥系统动态响应影响显著，故车辆动力参数(如表1所示)取值应尽可能与实际相符。车辆响应输出转向架上方底板处的横向和竖向振动加速度峰值。

表1 车辆的主要动力参数

1.2 轨道梁动力模型

选取跨座式单轨线路跨径25 m简支PC轨道梁，采用标准箱型0.85 m×1.5 m截面。采用有限元方法建立轨道梁振动微分方程(如式(2)所示)，计算模型中的单元均为空间离散梁单元，每个节点考虑6个运动自由度。

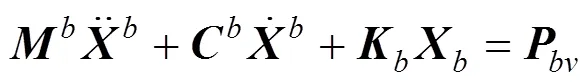
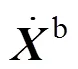
通过优化节点编号来缩减轨道梁动力模型中矩阵带宽，提高响应的求解效率。设定6等跨轨道梁，使得车辆和轨道梁的相互作用被充分激发，且梁体响应输出第3，4和5跨跨中振动位移和加速度峰值。

1.3 表面不平度

轨道梁的表面不平度是车辆在行驶过程中产生振动的重要外部激励，会对车桥动力响应产生影响。大量测试结果表明，路面纵剖面不平整度序列是一种随机现象，在数学上可近似表达为各态历经的平稳随机过程，即表面不平度激励下的车桥耦合振动从本质上来说属于一种随机振动现象。本研究采用文献[6−7]中根据实测数据确定的表面不平度功率谱密度函数(如式(3)所示)，图3为表面不平度功率谱密度函数图，所有工况均采用该样本值作为振动激励源。

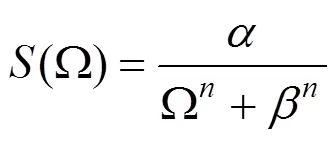
式中：(Ω)为轨道梁表面不平度的功率谱密度函数；Ω为空间频率，cycle/m；，和是功率谱密度函数的相关参数，取值如下：

走行轮：=0.000 5，=0.35，=3.00；

导向轮：=0.000 6，=0.50，=2.80；

稳定轮：=0.000 6，=0.50，=2.60。

图3 表面不平度功率谱密度

采用三角级数叠加法对功率谱密度函数进行数值模拟，得到轨道梁表面不平度的时域样本取值表达如式(4)，图4为模拟得到的走行轮、导向轮和稳定轮下轨道梁的表面不平度样本曲线。

式中：x为里程坐标；Ωi是所考虑频率点；ΔΩ为频率点间距；φi是在[0,2π]上均匀分布的随机相位。轨道梁表面不平度的输入方式是把车轮位置处的轨道梁振动位移、速度与表面不平度位移和速度分别叠加，用于计算轨道梁对车辆的作用力。

1.4 数值求解

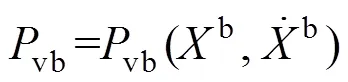
数值积分步长取Δ=0.1/，其中是列车行进速度。方程迭代的收敛依据为前后2次迭代间结构位移的最大差值不超过0.001 mm。

1.5 计算程序的检验

根据上述车辆−轨道梁动力相互作用理论模型与数值算法，编制跨座式单轨车桥空间耦合振动分析程序。为保证算法和程序的正确性，在分析前对计算程序进行必要的检验。

1.5.1 简谐不平度激励下的车辆响应

在走行轮下输入幅值为0.01 m的简谐不平度，车速为10 km/h。程序计算的车体竖向加速度幅值约为0.12 m/s2，根据车体的频率响应函数算出的车体理论稳态竖向加速度为0.12 m/s2，二者结果一致。

在导向轮和稳定轮下分别输入幅值为0.01 m的简谐不平度，车速为10 km/h。程序计算的车体横向位移幅值约为0.01 m，等同于车体横向理论位移值。

可见，在竖向和横向不平度激励下，程序计算得到的车辆响应均准确可靠。

1.5.2 车辆过桥时的轨道梁响应

考查单节车辆以30 km/h通过时简支轨道梁桥的动态响应。采用商业软件计算出移动荷载列作用下轨道梁跨中最大竖向挠度为8.5 mm，程序计算得车辆通过时轨道梁跨中竖向挠度最大值为8.3 mm，且二者的位移历程曲线吻合良好，表明该计算程序能准确反映车辆荷载作用下的轨道梁响应。

2 车桥动力响应分析

2.1 轨道梁自振特性分析

自振特性分析是轨道梁结构动力分析的基础。建立轨道梁有限元模型进行动力特性分析，表2列出了轨道梁的自振频率及振型。可以看出，轨道梁的横向和竖向基频较大，满足规范[15]要求的跨座式单轨轨道梁桥的横向自振频率不宜小于70/= 70/25=2.8 Hz，表明其动力特性优良。

表2 轨道梁的自振特性

2.2 车桥竖向动力响应

取三跨响应平均值作为分析数据，对不同车速、载客状态下轨道梁的竖向动力响应进行整理分析，竖向挠度和加速度峰值的变化曲线如图5所示。

由图5(a)观察可知，轨道梁跨中竖向动挠度的最大值随车速变化并不明显，与文献[9]中实测结果的规律一致；竖向挠度随载客量的提高而显著 增大。

由图5(b)观察可知，轨道梁跨中竖向加速度的峰值随车速先增大后趋于波动，并非随车速的增加而单调增大，与文献[8]实测值的变化趋势较为一致；竖向加速度受载客量影响较小。

(a) 竖向挠度；(b) 竖向加速度

计算通过弹性轨道梁时车辆的竖向振动响应，再计算车辆在通过具备相同不平度刚性地基时的竖向响应，二者差值即为轨道梁的动力行为单独引起车辆的竖向振动响应。

经计算整理，轨道梁动力行为对车体竖向振动加速度的影响程度如图6所示。观察可得，当车辆低速(≤35 km/h)运行时，轨道梁动力行为引起车辆竖向振动加速度的比例随车速和载客量的提高而增大；当车速大于40 km/h时，轨道梁的动力行为是引起车辆竖向振动的主要因素(约占比80%)，且几乎与车辆载客状态无关。

图6 轨道梁动力行为单独引起车体竖向加速度比例

对比分析图6与图5可得，轨道梁动力行为引起的车体竖向振动加速度比例与图5(a)跨中竖向挠度最大值的关系不显著，与图5(b)跨中竖向加速度峰值的波动趋势一致，进而推断出轨道梁动力行为中的竖向振动加速度决定着车体竖向振动水平。因此，强化对轨道梁竖向振动加速度的控制可有效提升跨座式单轨车辆的竖向走行性能。

2.3 车桥横向动力响应

参照车桥竖向响应的分析思路，探讨轨道梁动力行为对车辆横向振动响应的影响。将轨道梁跨中横向动力响应的最大值随车速和载客状态的变化情况整理如图7所示。

观察图7(a)可得，轨道梁跨中横向位移的峰值随车速先增后减，且变化幅度(不到1 mm)较小，40 km/h后趋于平稳，与文献[9]中波动较小的实测结果较一致，且受载客量的影响极小；

观察图7(b)可知，轨道梁跨中横向加速度的最大值随车速的提高呈上升趋势，与文献[9]实测结果的逐渐增大趋势较吻合，且基本不受载客状态 影响。

将轨道梁的动力行为与表面不平度的激励因素区分开来，前者对车辆横向振动加速度峰值的影响水平如图8所示。

(a) 横向位移；(b) 横向加速度

图8 轨道梁动力行为单独引起车体横向加速度比例

观察可得，轨道梁的动力行为单独引起车体横向振动加速度占比在40%与60%之间波动，且与车速和载客量的关系不明显。

对比分析可知，图8与图7(a)的曲线变化趋势相近，与图7(b)的关系不明确，表明轨道梁的动力行为中跨中横向位移是影响车体横向振动加速度的决定性成分。因此，强化对轨道梁横向变形的控制可进一步提高跨座式单轨车辆的横向走行性能。

3 结论

1) 轨道梁具备较大的横、竖向刚度，动力特性良好。

2) 轨道梁跨中竖向动挠度的最大值随车速变化不明显，随载客量的提高显著增大；跨中竖向加速度峰值并非随车速的增加而单调增大，且基本不受载客状态的影响。轨道梁的动力行为是引起车辆竖向振动的主要因素，强化对轨道梁竖向振动加速度的控制可有效提升车辆的竖向走行性能。

3)轨道梁跨中横向位移的最大值随车速先增后减，40 km/h后趋于平稳，且受载客量的影响极小；跨中横向加速度的最大值随车速的提高呈上升趋势，且基本不受载客状态影响。轨道梁的动力行为单独引起车体横向振动加速度占比在40%与60%之间波动，且与车速和载客量的关系不明显。强化对轨道梁横向变形的控制可进一步提高车辆的横向走行性能。

[1] 郭锴, 武农. 跨座式单轨交通的认识误区分析及发展展望[J]. 铁道标准设计, 2016, 60(3): 1−6. GUO Kai, WU Nong. Eliminate misunderstanding and promote development of straddle monorail[J]. Railway Standard Design, 2016, 60(3): 1−6.

[2] 仲建华, 杜子学, 何希和. 跨座式单轨交通车辆道岔结构及分析[M]. 北京: 人民交通出版社, 2013: 1−10. ZHONG Jianhua, DU Zixue, HE Xihe. Vehicle switch structure and analysis of straddle-type monorail transportation[M]. Beijing: China Communication Press, 2013: 1−18.

[3] 翟婉明, 夏禾. 列车−轨道−桥梁动力相互作用理论与工程应用[M]. 北京: 科学出版社, 2011: 1−7. ZHAI Wanming, XIA He. Train-track-beidge dynamic interaction: Theory and engineering application[M]. Beijing: Science Press, 2011: 1−7.

[4] 杜子学, 李云川, 梁志华, 等. 跨座式单轨车辆曲线通过安全性研究[J]. 机车电传动, 2016(1): 79−83. DU Zixue, LI Yunchuan, LIANG Zhihua, et al. Research on curve through safety of straddle-type monorail vehicle[J]. Electric Drive for Locomotives, 2016(1): 79−83.

[5] 周小苏. 跨座式轨道梁横向自振频率的简化计算方法[J]. 铁道建筑, 2017(8): 15−17. ZHOU Xiaosu. A simplified calculation method of transverse natural vibration frequency of straddled track beam[J]. Railway Engineering, 2017(8): 15−17.

[6] Chang Hun Lee, Chul Woo Kim. Dynamic response analysis of monorail bridges under moving trains and riding comfort of trains[J]. Engineering Structures, 2005, 27(14): 1999−2013.

[7] Lee C H, Kawatani M. Dynamic response of a monorail steel bridge under a moving train[J]. Journal of Sound and Vibration, 2006(294): 562−579.

[8] 马继兵. 跨座式单轨交通系统结构静动力行为研究[D]. 成都: 西南交通大学, 2008. MA Jibing. Research on structural static and dynamic behaviors of straddle-type monorail transportation system[D]. Chengdu: Southwest Jiaotong University, 2008.

[9] 施洲，蒲黔辉，高玉峰，等. 重庆市跨座式单轨交通系统动力试验研究[J]. 振动与冲击, 2008, 27(12): 101− 106. SHI Zhou, PU Qianhui, GAO Yufeng, et al. Dynamic test of straddle-type monorail transportation system in Chongqing[J]. Journal of Vibration and Shock, 2008, 27(12): 101−106.

[10] 刘羽宇, 葛玉梅, 杨翊仁. 跨座式单轨列车与轨道梁系统的动力响应分析[J]. 中国铁道科学, 2010, 31(5): 21−27. LIU Yuyu, GE Yumei, YANG Yiren. The dynamic response analysis of the coupled system of the straddle type monorail train and the track beam[J]. China Railway Science, 2010, 31(5): 21−27.

[11] 刘羽宇, 葛玉梅, 杨翊仁. 跨座式单轨交通系统耦合振动特性[J]. 交通运输工程学报, 2010, 10(2): 46−53. LIU Yuyu, GE Yumei, YANG Yiren. Vibration characteristic of coupled system for straddle type monorail beam and train[J]. Journal of Traffic and Transportation Engineering, 2010, 10(2): 46−53.

[12] 张凯. 跨座式单轨交通曲线梁桥车桥耦合振动分析[D]. 北京: 北京交通大学, 2012. ZHANG Kai. Analysis of bridge-vehicle coupling vibration on curve bridge of straddle monorail transit[D]. Beijing: Beijing Jiaotong University, 2012.

[13] 乔志. 跨座式单轨交通车辆−轨道梁耦合系统动力问题研究[D]. 北京: 北京交通大学, 2016. QIAO Zhi. Study of straddle monorail train-track beam coupling system dynamics[D]. Beijing: Beijing Jiaotong University, 2016.

[14] 张晓波. 桥梁刚度对车辆走行性影响的有限元分析[D].兰州: 兰州交通大学, 2016. ZHANG Xiaobo. Finite element analysis of the influence of the stiffness of the bridge on the walking behavior of vehicles[D]. Lanzhou: Lanzhou Jiaotong University, 2016.

[15] 刘国. 跨座式单轨交通轨道梁刚度对乘坐舒适性影响研究[J]. 铁道勘察, 2016, 42(1): 85−88. LIU Guo. Study on the influence of track-beam stiffness on straddle monorail transit ride comfort[J]. Railway Investigation and Surveying, 2016, 42(1): 85−88.

[16] GB 50458—2008, 跨座式单轨交通设计规范[S]. GB 50458—2008, Code for design of straddle monorail transit[S].

(编辑 蒋学东)

Influence of track beam’s dynamic behavior on running performance of straddle-type monorail vehicle

LI Xiaozhen, GE Yanlong, JIN Zhibin, ZHU Yan

(School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China)

When the straddle-type monorail vehicle passes through track beam bridge, the vibration and deformation of track beam will conversely influence the running performance of vehicle. In order to explore the impact level of track beam’s dynamic behavior on vehicle’s response, a spatial coupling model of straddle-type monorail vehicle-track beam was established in the study. Dynamic responses of vehicle-bridge in the section of track beam and subgrade under conditions of different speed and passenger volume were calculated and analyzed. The study shows that standard PC track beam performs good. Maximum vertical deflection at mid-span of the track beam is inconspicuously related to vehicle speed, yet significantly increases with the augmentation of passenger. The transverse displacement peak at mid-span is independent from passenger volume, which increases at first and then decreases with the speed. Vertical acceleration of track beam at mid-span firstly increases along with the speed and then tends to fluctuate, and transverse acceleration keeps rising all through. However, both vertical and transverse accelerations are irrelevant to the change of passenger volume. Furthermore, dynamic behavior of the track beam is the main factor determining the vertical acceleration of vehicle, the percentage of which singly leads to the vehicle transverse acceleration is 50% or so. Strengthening the control of vertical vibration and transverse deformation of the track beam shall effectively improve the running performance of vehicle.

straddle-type monorail transit; track beam; passenger volume; dynamic response; running performance

10.19713/j.cnki.43−1423/u.2018.12.027

U232；U 441+.3

A

1672 − 7029(2018)12 − 3225 − 07

2017−11−27

国家自然科学基金重点资助项目(U1434205, 51708465)；国家重点基础研究发展计划(973计划)项目(2013CB036301)；中国铁路总公司科技研究开发计划资助项目(2015G002-A)

朱艳(1979−)，女，湖南湘潭人，讲师，博士，从事车桥耦合振动与桥梁动力行为研究；E−mail：8988zhu@163.com