疲劳裂纹扩展引起的钢轨表面剥离研究

昝晓东，李孝滔，邢帅兵，张言库，江晓禹

疲劳裂纹扩展引起的钢轨表面剥离研究

昝晓东，李孝滔，邢帅兵，张言库，江晓禹

(西南交通大学 力学与工程学院，四川 成都 610031)

钢轨表面疲劳裂纹扩展引起的剥离掉块是一种很常见的损伤形式。利用有限元模拟钢轨表面裂纹扩展，得到裂纹尖端的周向应力和应力强度因子。基于最大周向应力幅值判据，确定裂纹扩展方向，运用paris公式计算裂纹扩展速率，进而确定裂纹扩展路径。研究结果表明：高速列车裂纹扩展速率明显高于低速列车。高速列车钢轨经过6万多次车轮碾压表面剥离，剥离深度约为430 μm；而低速列车钢轨经过16万多次车轮碾压表面剥离，剥离深度约为590 μm。模拟的钢轨裂纹扩展路径和剥离掉块与现场服役钢轨的损伤形貌比较吻合，说明用最大周向应力幅值判据来确定钢轨疲劳裂纹扩展路径是可行的。钢轨表面剥离与疲劳裂纹扩展密切相关，建议对钢轨进行及时的打磨来预防钢轨的剥离。

ANSYS；轮轨接触疲劳；最大周向应力幅值；裂纹扩展；剥离

轮轨滚动接触疲劳一直是铁路工业中难以解决的老问题，随着铁路客货运量的增大和列车速度的提高，轮轨滚动接触疲劳所造成的破坏变得越来越严重。它不仅大大增加铁路的运营成本 ,而且直接危害行车安全[1]。钢轨钢的接触疲劳研究越来越受到人们的重视，钢轨表面疲劳裂纹扩展行为的研究是疲劳分析一个重要部分[2−4]。Seo等[5]采用双圆盘试验研究了钢轨表面裂纹扩展行为。郭火明等[6]利用现代先进观测技术对现场铁路损伤钢轨进行了测试分析，并对钢轨损伤机理进行了分析。李孝滔等[7]用概率统计的方法对钢轨裂纹扩展进行了研究。卢观健等[8]对钢轨的损伤形态进行了分析，指出钢轨表面经过碾压出现鱼鳞状剥离裂纹，随后发展成剥离掉块。陈颜堂等[9]的研究结果表明相互平行的裂纹 ,经车轮的反复碾压后出现剥落。对于Ⅰ-Ⅱ复合型裂纹扩展方向的确定，很多学者[10−12]提出了相关的理论。这些理论通常用于比例单调加载的情况，不能直接用来确定轮轨接触疲劳裂纹的扩展方向[13]。LI等[14]提出了最大周向应力幅值判据，并且对疲劳加载下复合型裂纹扩展方向进行了预测，预测结果与实验结果基本一致。本论文应用最大周向应力幅值判据来确定钢轨疲劳裂纹扩展方向。在钢轨表面预设2条平行初始裂纹，模拟钢轨疲劳裂纹的扩展，裂纹扩展交汇导致钢轨表面剥离。模拟结果与实际钢轨损伤形貌比较吻合。

1 钢轨疲劳裂纹扩展理论介绍

1.1 研究模型

轮轨接触的研究模型如图1所示，车轮以水平速度在钢轨上向前滚动，车轮(轮重=5 t)在钢轨上作纯滚动，根据文献[8−9]对实际钢轨表面裂纹和剥离研究，在钢轨表面预设2条平行微裂纹(裂纹①和裂纹②)，裂纹长度100 μm，裂纹与行车方向的夹角均为30°。轮轨间的接触作用力为法向接触压力和切向摩擦力。

1.2 最大周向应力幅值判据

车轮碾压下的钢轨表面疲劳裂纹承受交变荷载。疲劳裂纹扩展过程比较复杂，受很多因素的影响，应力幅值是影响裂纹扩展的主要因素。用最大周向应力幅值判据可以有效预测疲劳裂纹扩展方向。裂纹尖端周向应力幅值为：

图1 轮轨滚动接触研究模型

1.3 裂纹扩展速率

2 钢轨滚动接触疲劳有限元模拟

本次模拟的钢轨为我国铁路干线大量使用的U71Mn钢，钢轨材料参数[18−19]如表1所示。

表1 U71Mn钢的力学性能

根据我国使用的60 kg/m钢轨的几何尺寸，有限元模型为二维含表面裂纹的钢轨模型，且为平面应变问题。有限元模型高为176 mm，长为1 000 mm；裂纹间距500 μm，裂纹方向与行车方向夹角为30°；有限元模型使用8节点的PLANE183单元，裂纹尖端采用1/4节点的奇异单元，单元尺寸10 μm。并且在裂纹面设置接触，接触摩擦因数为0.2。不考虑轨枕的影响，钢轨下端采取全约束。钢轨整体有限元模型与裂纹尖端局部有限元模型如图2。

(a) 整体模型网格；(b) 局部放大图网格

下面主要研究在轮轨接触荷载作用下2条平行裂纹的扩展情况。荷载为车轮作纯滚动时对钢轨表面的接触压力和切向摩擦力，随着车轮的滚动而移动。取列车运行速度50 km/h(低速)和350 km/h(高速)分别进行研究。在考虑轮轨高速滚动的材料变形所引起的应变率效应和真实轮轨外形情况下，获得不同速度列车轮轨载荷分布[13]如图3。从图3中可见，高速滚动时的法向接触压力与低速情况有些不同，低速滚动时接触压力分布与Hertz接触应力分布相近，而高速滚动情况出现2个峰值，但大小相差不大。摩擦力分布出现明显的不同，主要是由于的高低速风阻力不同引起。而这种接触作用力分布的不同将进一步影响到钢轨表面微裂纹扩展速率和破坏模式的差异。

图3 轮轨滚动接触荷载分布

3 钢轨滚动接触疲劳与表面剥离

3.1 裂纹扩展方向分析

车轮在钢轨上作纯滚动时，钢轨表面裂纹受法向压力和切向摩擦力会反复引起裂纹的张开与闭合。为了确定疲劳裂纹的扩展方向，需要计算车轮移动过程中在裂纹附近多个位置处的受力情况。图4显示的是轮轨载荷相对钢轨表面裂纹的位置，图中为荷载接触斑右端相对裂纹①的距离，定义为裂纹角度(裂纹与行车方向的夹角，顺时针方向为正)，定义为裂纹扩展角度(裂纹与裂纹扩展方向的夹角，顺时针方向为正)。轮轨载荷每移动到一个计算位置，计算出裂纹尖端附近周向应力。图5显示了50 km/h列车钢轨表面裂纹①的初始裂纹尖端周向应力随的变化情况，其他裂纹采用相同的计算方法。

图4 移动荷载示意图

图5 裂纹①的初始裂纹尖端周向应力分布情况

用公式(1)计算各角度的周向应力幅值，钢轨疲劳裂纹扩展过程中周向应力幅值随的变化如图6~7所示。其中图6显示了不同车速下裂纹①的初始裂纹尖端周向应力幅值随的变化，图7显示了50 km/h列车钢轨表面裂纹①后续裂纹尖端应力幅值随的变化。从图6~7看出初始裂纹第1次扩展的偏转角度较大，约为60°左右，随后裂纹扩展角度变小。从图6看出，约为−30°(周向应力方向与轮轨切向摩擦力方向垂直)时，高速和低速列车钢轨表面裂纹尖端的周向应力幅值几乎相等，在约为60°(周向应力方向与轮轨切向摩擦力方向平行)时，高速列车钢轨表面裂纹尖端的周向应力幅值明显大于低速列车。结合高速和低速列车的轮轨载荷的分布，切向摩擦力是影响不同车速下裂纹尖端周向应力幅值的关键因素，而且周向应力方向越接近摩擦力的方向，影响越大。

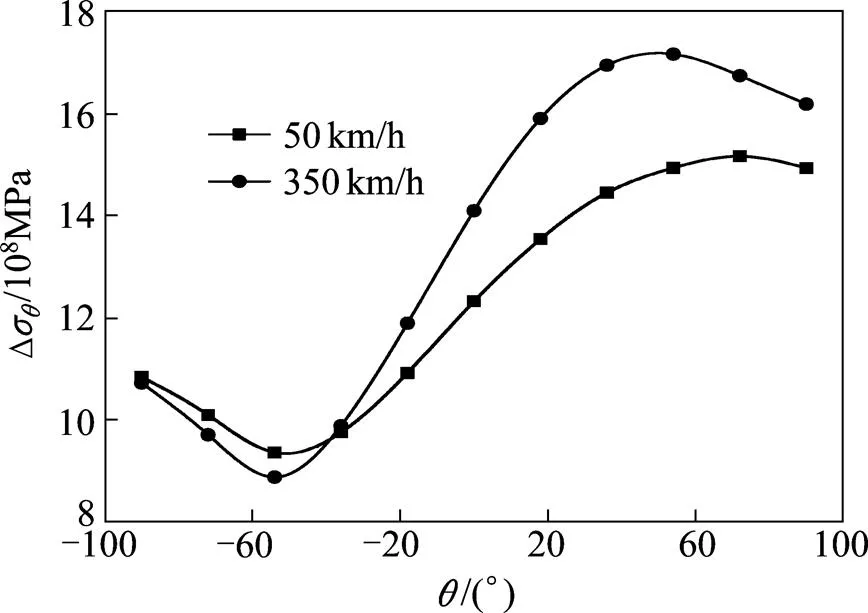
图6 不同车速下裂纹①的初始裂纹尖端周向应力幅值分布

图7 裂纹①的裂纹尖端周向应力幅值分布

根据周向应力幅值随的变化趋势，用式(2)来确定裂纹的扩展角度。表2和表3分别记录了50 km/h和350 km/h列车钢轨表面裂纹扩展过程中各段裂纹的扩展角度。

表2 50 km/h列车钢轨裂纹长度及扩展角度的结果

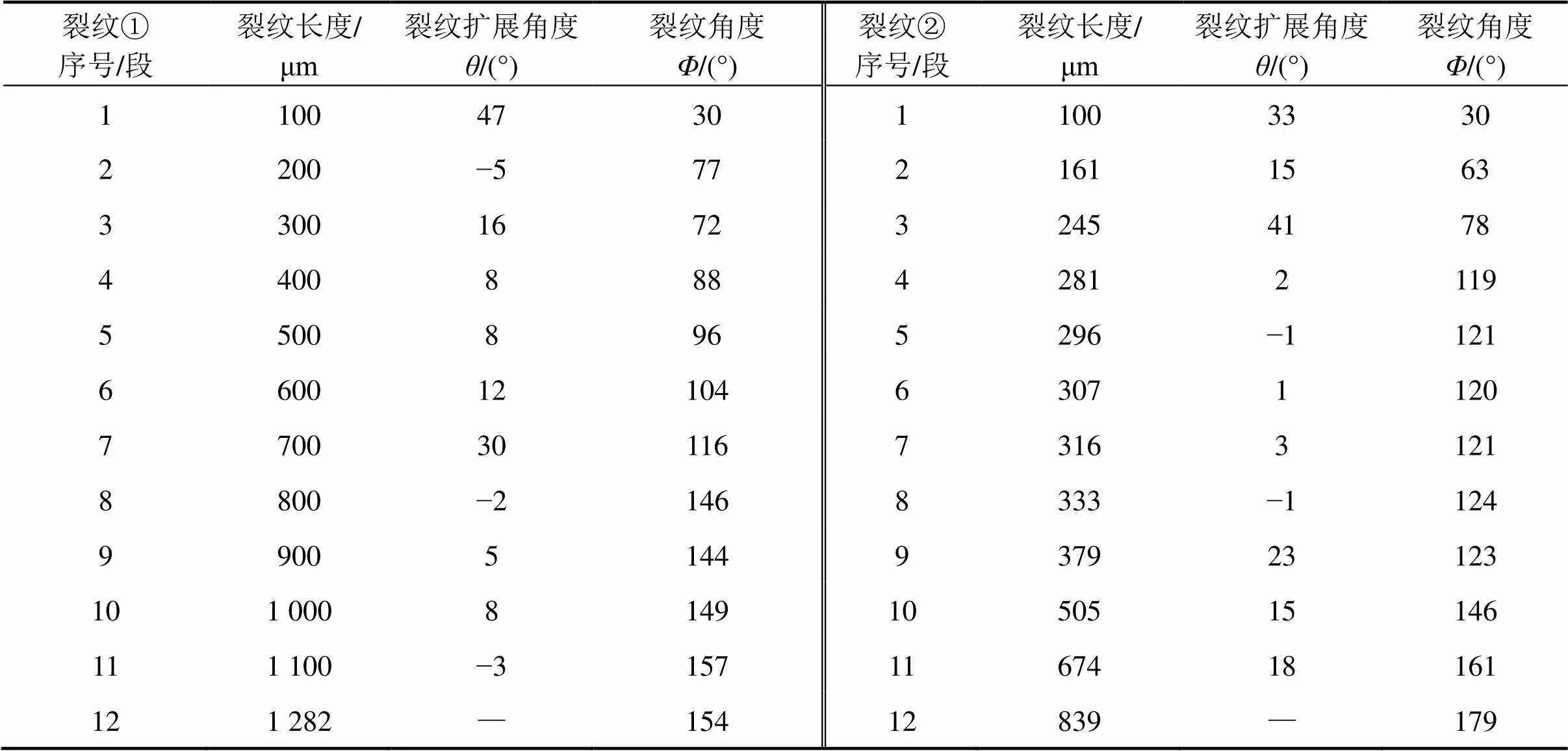
表3 350 km/h列车钢轨裂纹长度及扩展角度的结果

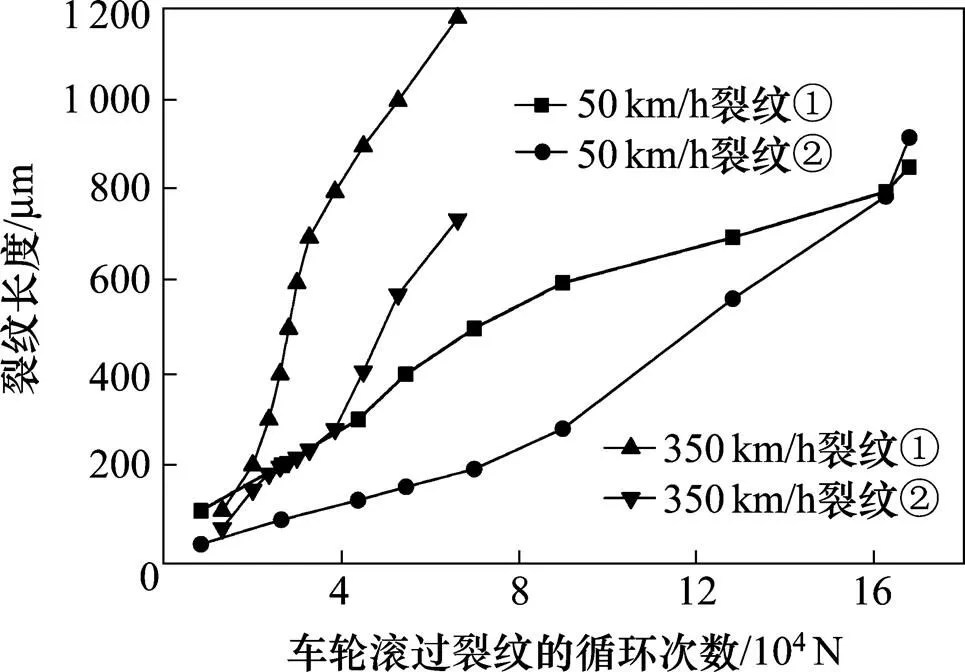
图8 裂纹扩展长度随车轮滚过次数的变化

3.2 裂纹扩展速率与表面剥离分析

参照1.2节描述的裂纹扩展速率理论，计算出裂纹扩展过程中各段的疲劳扩展速率。计算过程中用到的U71Mn钢的疲劳裂纹扩展参数从文献[20]中获取，其中=4.597×10−13，=2.88。随着车轮滚过次数的增加，裂纹扩展长度不断增加直到钢轨表面剥离。图8显示了不同列车速度下，钢轨表面裂纹的长度随车轮滚过次数的变化情况。由图8可以看出，高速列车钢轨表面裂纹的扩展速率明显要大于低速列车，这是因为高速列车作用在钢轨的摩擦力要明显大于低速列车。在预制了100 μm初始裂纹的情况下，高速列车车轮滚过6万多次，钢轨表面出现剥离，而低速列车车轮滚过16万多次，钢轨表面才出现剥离。

3.3 裂纹扩展路径分析

为了模拟2条裂纹扩展路径，裂纹①每次扩展长度定为100 μm，裂纹②的扩展长度根据2条裂纹的扩展速率比来确定，高速和低速列车钢轨表面裂纹在每阶段的扩展角度和裂纹长度如表2和表3。根据裂纹扩展长度和扩展角度模拟出裂纹的扩展路径。图9展现了高速和低速列车钢轨表面裂纹扩展路径与朔黄线服役钢轨[21]裂纹路径对比情况。图10展现了高速和低速列车钢轨表面剥离与大秦线服役钢轨[6]表面剥离形貌对比情况。从图9看出，不论是高速还是低速列车，钢轨表面裂纹前期扩展路径都与列车运行方向基本成90°，向钢轨内部扩展，随着裂纹长度增加，裂纹沿着与列车运行方向相反的方向扩展，形成鱼钩形裂纹，这与文献[13]描述的基本一致。高速时，裂纹扩展在向深度方向前进过程中，裂纹②在更浅的地方出现了偏转，导致钢轨表面剥离较浅。从图10看出，模拟的高速列车钢轨表面的剥离比低速列车的浅，高速列车的剥离深度约为430 μm，低速列车的剥离深度约为590 μm，但模拟的2种速度列车的钢轨剥离都比现场服役钢轨的剥离深，这是因为在模拟过程中未考虑钢轨磨损。模拟的钢轨裂纹扩展路径和剥离形貌同现场服役钢轨裂纹扩展路径和形貌比较吻合，说明用最大周向应力幅值判据来判断钢轨疲劳裂纹扩展方向是可行的。

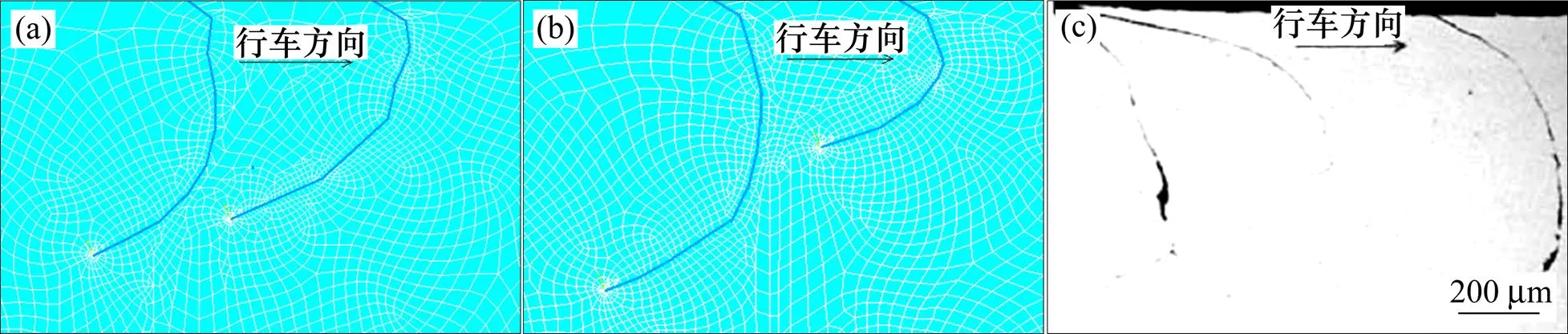
(a) 50 km/h；(b) 350 km/h；(c) 实际钢轨

(a) 50 km/h；(b) 350 km/h；(c) 实际钢轨

4 结论

1) 无论列车是高速还是低速，在初期扩展阶段，钢轨表面2条裂纹扩展方向基本在垂直方向；随着裂纹长度增加裂纹沿着与行车方向相反的方向扩展，形成鱼钩型裂纹。裂纹继续扩展，2条裂纹相交，钢轨表面剥离。

2) 350 km/h列车钢轨裂纹扩展速率明显高于50 km/h列车钢轨裂纹扩展速率。经过6万多次车轮碾压，350 km/h列车钢轨表面剥离。经过16万多次车轮碾压，50 km/h列车钢轨表面剥离。

3) 模拟的裂纹扩展路径与现场服役钢轨裂纹形貌基本吻合，说明用最大周向应力幅值判据来判断钢轨疲劳裂纹扩展方向是可行的。

4) 钢轨的剥离掉块与疲劳裂纹的扩展密切相关，建议对钢轨进行及时的打磨，磨掉钢轨的表层，防止萌生的表层裂纹进一步扩大，从而造成钢轨的剥离掉块。

[1] 金学松, 沈志云. 轮轨滚动接触疲劳问题研究的最新进展[J]. 铁道学报, 2001, 23(2): 92−108. JIN Xuesong, SHEN Zhiyun. Rolling contact fatigue of wheel/rail and its advanced research progress[J]. Journal of the China Railway Society, 2001, 23(2): 92−108.

[2] Kondo K, Yoroizaka K, Sato Y. Cause, increase, diagnosis, countermeasures and elimination of Shinkansen shelling[J]. Wear, 1996, 191(1−2): 199−203.

[3] Caooan D F, Pradier H. Rail rolling contact fatigue research by the European rail research institute[J]. Wear, 1996, 191(1−2): 1−13.

[4] WANG L, Pyzalla A, Stadlbauer W, et al. Microstructure features on rolling surfaces of railway rails subjected to heavy loading[J]. Materials Science & Engineering A, 2003, 359(1): 31−43.

[5] Seo J W, Kwon S J, Lee D H, et al. Analysis of contact fatigue crack growth using twin-disc tests and numerical evaluations[J]. International Journal of Fatigue, 2013, 55(55): 54−63.

[6] 郭火明, 王文健, 刘腾飞, 等. 重载铁路钢轨损伤行为分析[J]. 中国机械工程, 2014, 25(2): 267−272. GUO Huoming, WANG Wenjian, LIU Tengfei, et al. Analysis of damage behavior of heavy-haul railway rails[J]. China Mechanical Engineering, 2014, 25(2): 267−272.

[7] 李孝滔, 李煦, 曹世豪, 等. 基于概率统计方法对钢轨疲劳裂纹路径的研究[J]. 表面技术, 2015, 44(11): 71−78. LI Xiaotao, LI Xu, CAO Shihao, et al. Rail fatigue crack path based on probabilistic and statistical method[J]. Surface Technology, 2015, 44(11): 71−78.

[8] 卢观健, 杨克. 钢轨伤损的形态特征及其失效机理[J]. 铁道学报, 1996(3): 120−124. LU Guanjian, YANG Ke. Morphological characteristics and failure mechanism of rail damage[J]. Journal of the China Railway Society, 1996(3): 120−124.

[9] 陈颜堂, 刘东雨, 方鸿生, 等. 钢轨钢的滚动接触疲劳[J]. 钢铁研究学报, 2000, 12(5): 50−53. CHEN Yantang, LI Dongyu, FANG Hongsheng, et al. Rolling contact fatigue of rail steel[J]. Journal of Iron & Steel Research, 2000, 12(5): 50−53.

[10] Sih G C. Methods of analysis and solutions of crack problems[M]. Springer Netherlands, 1973.

[11] Palaniswamy K, Knauss W G. Propagation of a crack under general, in-plane tension[J]. International Journal of Fracture Mechanics, 1972, 8(1): 114−117.

[12] Richard H A, Fulland M, Sander M. Theoretical crack path prediction[J]. Fatigue & Fracture of Engineering Materials & Structures, 2005, 28(1−2): 3−12.

[13] 江晓禹, 李孝滔, 李煦, 等. 轮轨高速滚动接触及钢轨疲劳裂纹扩展研究[J]. 西南交通大学学报, 2016, 51(2): 274−281. JIANG Xiaoyu, LI Xiaotao, LI Xu, et al. Research on wheel/rail rolling contact at high speed and fatigue crack propagation in rail[J]. Journal of Southwest Jiaotong University, 2016, 51(2): 274−281.

[14] LI X T, JIANG X Y, LI X, et al. Solution of an inclined crack in a finite plane and a new criterion to predict fatigue crack propagation[J]. International Journal of Mechanical Sciences, 2016, 119: 217−223.

[15] 郦正能. 工程断裂力学[M]. 北京: 北京航空航天大学出版社, 2012: 135−145. LI Zhengneng. Engineering fracture mechanics[M]. Beijing: Beijing Aeronautics and Astronautics University Press, 2012: 135−145.

[16] Paris P C, Erdogan F. A critical analysis of crack propagation laws[J]. Journal of Basic Engineering, 1963, 85(4): 528−533.

[17] Tankan K. Fatigue crack propagation from a crack inclined to the cyclic tensile axis[J]. Engineering Fracture Mechanics, 1974, 6(3): 493, IN13, 499−498, IN14, 507.

[18] 周小林, 向延念, 陈秀方. U71Mn 50 kg/m普通碳素钢钢轨疲劳裂纹扩展速率试验研究[J]. 中国铁道科学, 2004, 25(3): 86−90. ZHOU Xiaolin, XIANG Yannian, CHEN Xiufang. Test and study of fatigue fracture propagation of U71Mn 50 kg/m ordinary carbon steel rail[J]. China Railway Science, 2004, 25(3): 86−90.

[19] 曹世豪, 李煦, 文良华, 等. 钢轨表面裂纹扩展方向研究[J]. 表面技术, 2014(3): 37−42. CAO Shihao, LI Xu, WEN Lianghua, et al. Analysis of propagation direction of rail surface crack[J]. Surface Technology, 2014, 43(3): 37−42.

[20] 王文健, 刘启跃. PD3和U71Mn钢轨钢疲劳裂纹扩展速率研究[J]. 机械强度, 2007, 29(6): 1026−1029. WANG Wenjian, LIU Qiyue. Study on fatigue crack growth rate of PD3 and U71Mn rail steel[J]. Journal of Mechanical Strength, 2007, 29(6): 1026−1029.

[21] 陈朝阳, 张银花, 刘丰收, 等. 朔黄铁路曲线下股热处理钢轨剥离伤损成因分析[J]. 中国铁道科学, 2008, 29(4): 28−34. CHEN Zhaoyang, ZHANG Yinhua, LIU Fengshou, et al. Analysis on the formation cause of spalling and damage of the heat-treated low rail on Shuohuang railway curve[J]. China Railway Science, 2008, 29(4): 28−34.

(编辑 涂鹏)

Analysis of rail surface shelling resulting from fatigue crack propagation

ZAN Xiaodong, LI Xiaotao, XING Shuaibing, ZHANG Yanku, JIANG Xiaoyu

(School of Mechanics and Engineering, Southwest Jiaotong University, Chengdu 610031, China)

The rail shelling caused by rail fatigue crack propagation is a common problem. Circumferential stress and stress intensity factors at crack tip were calculated by finite element simulation. In order to predict the crack propagation path for wheel/rail rolling contact fatigue, the cracks propagation direction and propagation rate need to be known. Based on the maximum circumferential stress amplitude criterion, the direction of crack propagation was determined. The crack propagation rate was calculated by Paris’ law. The results show that the crack propagation rate of the high-speed train is significantly higher than the low-speed train. After about 60 thousand cycles, the high-speed train rail surface appears shelling whose depth is about 430 μm; after about 160 thousand cycles, the low-speed train rail surface appears shelling whose depth is about 590 μm. The simulated rail crack paths are relatively consistent with the damage morphology of the service rail, which proves it is feasible that the maximum circumferential stress amplitude criterion is applied to predict rail fatigue crack propagation. The shelling and fatigue crack growth of rail are closely related, so it is important to polish rail surface timely.

ANSYS; wheel/rail contact fatigue; maximum circumferential stress amplitude; crack propagation; shelling

10.19713/j.cnki.43−1423/u.2018.12.009

U211.5

A

1672 − 7029(2018)12 − 3082 − 07

2017−12−24

国家自然科学基金重点面上资助项目(11472230)

江晓禹(1965−)，男，贵州遵义人，教授，博士，从事复合材料力学和固体接触力学方面的研究；E−mail：xiaoyujiang8@sina.com