重型燃气轮机端面弧齿动力学特性及动应力研究
2018-12-17袁淑霞张优云朱永生
袁淑霞, 张优云, 朱永生
(1.西安石油大学 机械工程学院,西安 710065;2.西安交通大学 润滑理论及轴承研究所,西安 710049)
端面弧齿被广泛应用于航空发动机和重型燃气轮机中,通过一根中心拉杆或多根周向拉杆将侧面带有弧齿的轮盘组合在一起。端面弧齿具有联接定位可靠、定心精确、稳定性好和承载能力强等特点,但其形状复杂,理论分析难度较大,相关研究工作进展缓慢且以静力学研究为主。
Pisani等[1]采用有限元和边界元法研究了单个齿非接触模型,得出端面弧齿的应力集中因子。Richardson等[2-3]通过光弹实验验证了接触有限元法计算端面弧齿接触应力的可行性,并研究了拉杆在叶片断裂时的应力变化。Jiang等[4]也研究了叶片断裂对端面弧齿应力的影响。Yuan等[5]对端面弧齿拉杆预紧过程进行了研究。Muju等[6]对端面弧齿齿根进行了优化,从减小应力集中角度提出了复合圆角设计。Jiang等[7-9]对端面弧齿结构螺栓预紧松弛进行了研究。Yuan等[10]研究了端面弧齿两端薄壁结构对端面弧齿应力分布的影响。
相比以上静应力的研究,对于动应力的研究较少。Cavatorta等[11]采用有限元法研究了汽车螺栓联接结构循环载荷下的动应力以及疲劳问题。Whalley等[12]计算了轴承-转子系统的动应力问题。Purcell[13]采用NASTRAN软件分析了燃气轮机叶轮的动应力问题。袁淑霞等[14]研究了拉杆转子失谐时的动应力。
对于拉杆联接的端面弧齿转子,有弯曲力作用时,端面弧齿将随着弯曲力的动态变化产生动应力。Yuan等[15]研究了端面弧齿转子中单个齿的应力分布规律,而将其扩展到动应力的研究需要结合转子的动力学研究结果。笔者首先进行转子动力学分析,并采用Ansys软件建立端面弧齿转子接触有限元模型,分析端面弧齿在预紧力、离心力和扭矩力作用下的应力分布规律,最后将动力学分析结果作为位移边界条件施加于静力学分析模型上,研究动态弯曲力作用下端面弧齿的动应力分布规律。
1 端面弧齿动应力分布计算模型
1.1 动力学分析模型
接触界面处的不连续决定了端面弧齿转子与整体转子在受力方式上的不同,同时也会影响转子的动态特性。葛庆等[16]采用修正系数修正了端面弧齿联接段的刚度。Yuan等[17]则提出了更为精确的拉杆转子等效抗弯刚度模型,该模型是基于转子弯曲时中性层两侧的受压侧压力由接触界面承受,受拉侧拉力由拉杆承受的原理提出的(见图2),其中性层位置亦随弯矩发生变化。
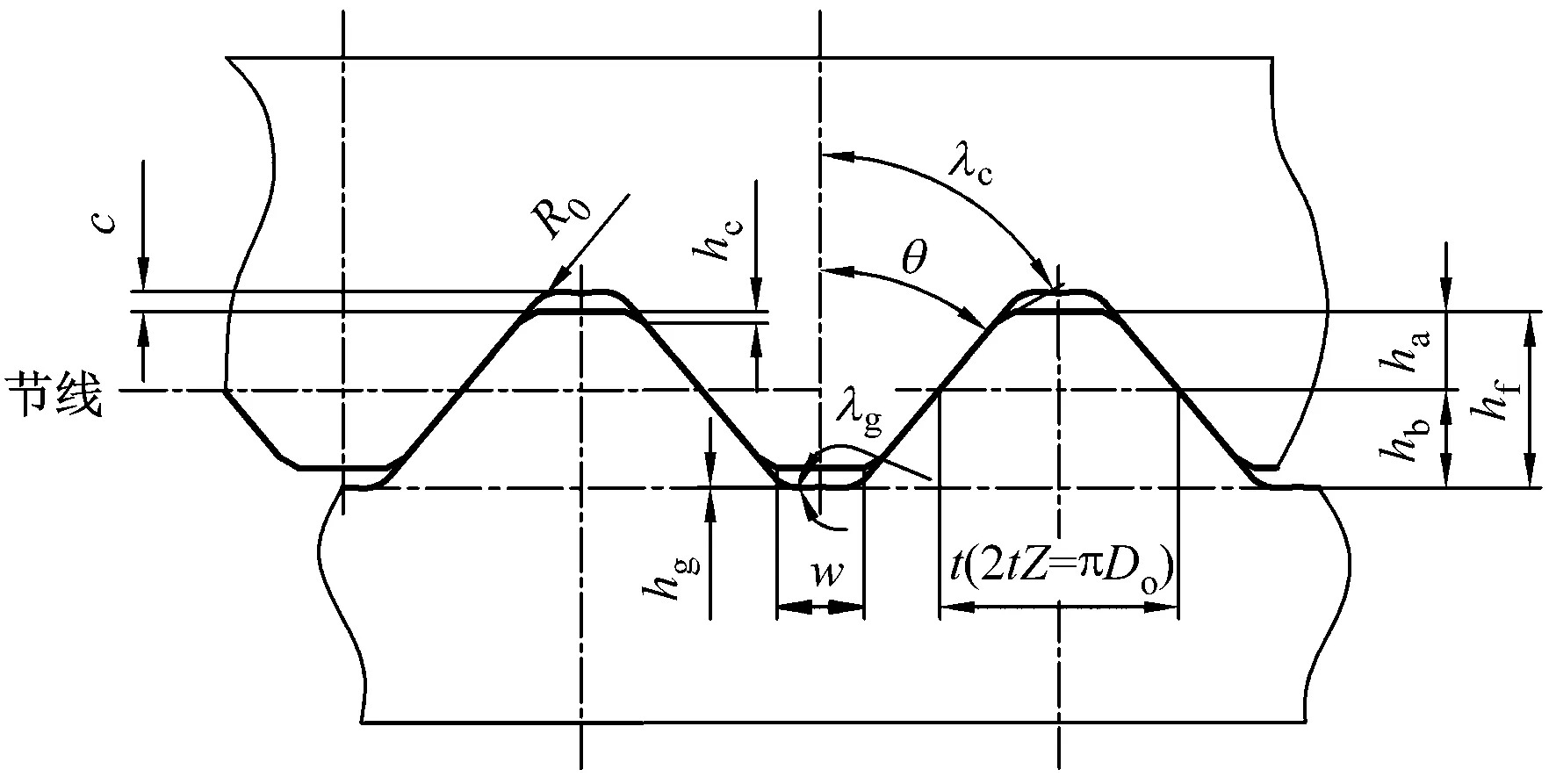
图1 端面弧齿外径处径向展开图
抗弯刚度由两部分组成:一部分是受压侧的接触界面抗弯刚度;另一部分是受拉侧的拉杆抗弯刚度,见式(1)。在接触区域采用该模型,连续区域采用传统方法计算抗弯刚度,建立刚度矩阵,研究转子的动态响应。
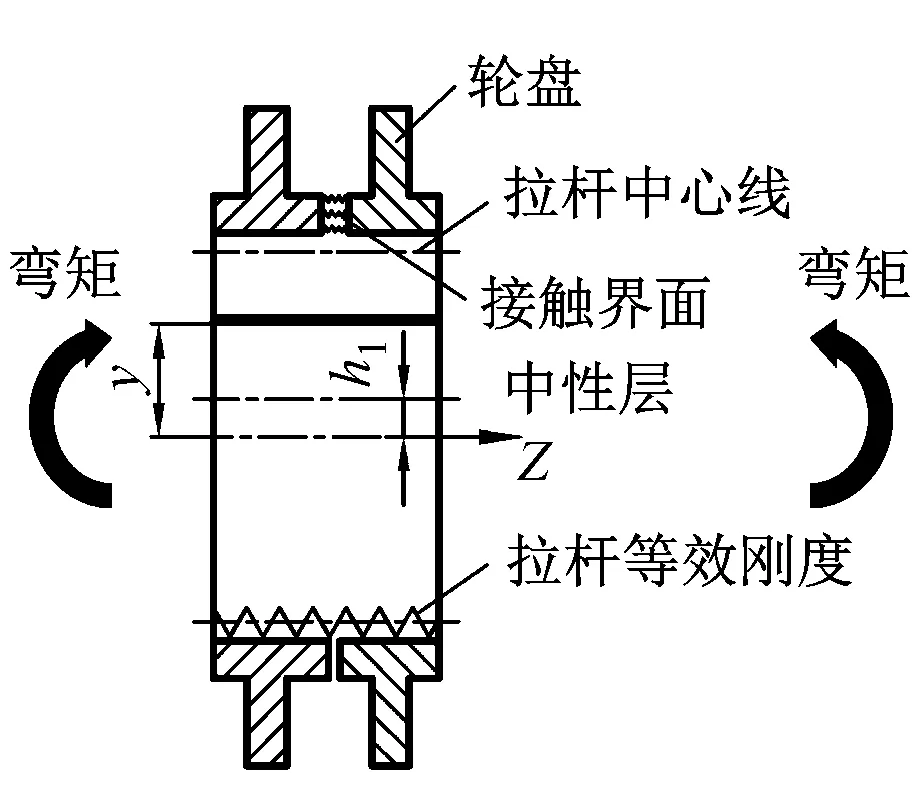
(1)
式中:EI为转子等效刚度,N·m2,其中E为弹性模量,I为惯性矩,m4;Ew为轮盘材料弹性模量,Pa;y为接触界面微元体距X(Z)轴距离,m;dA为该微元体面积,m2;Er为拉杆材料弹性模量,Pa;Ar为拉杆横截面积,m2;hl为中性层与X(Z)轴距离,m;n为拉杆数;Rr为拉杆中心圆半径,m;σri为第i个拉杆的应力,Pa,只有该拉杆应力为正(受拉)时计入。
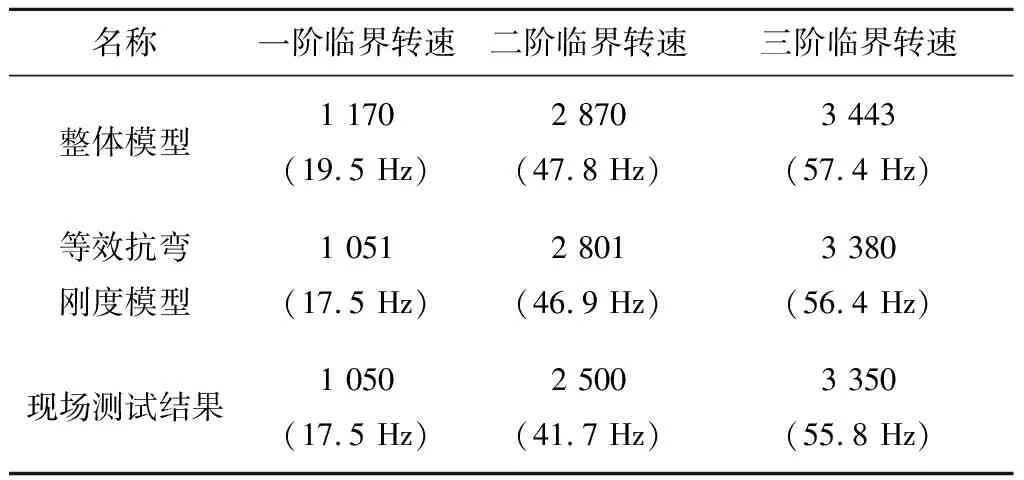
根据转子的形状特征及接触界面的分布,将重型燃气轮机转子划分为47个单元(48个节点),见图3。轮盘中心、轴颈中心、截面突变处、轴的端部以及接触界面影响区和非影响区的交界处均需设置节点。叶片和轮盘考虑集中质量和转动惯量,加到相应节点上,轴段质量和转动惯量采用插值函数进行积分。进气端和排气端分别设置了径向支承轴承(见图3)。该轴承为固定-可倾瓦轴承,上瓦为固定瓦,下瓦为可倾瓦,轴承的刚度和阻尼系数不作为本文研究内容,按照生产厂商提供的数据进行计算。将通过式(1)所述等效抗弯刚度模型计算的转子临界转速与按整体转子计算的结果和现场测试结果进行对比,结果见表1。从表1可以看出,按照等效抗弯刚度模型计算的临界转速更接近现场测试结果。因此在计算转子动态响应时接触界面处采用式(1)等效的抗弯刚度。

图3 重型燃气轮机转子示意图及离散方法
Tab.1Comparisonofcriticalrotorspeedsfortheheavy-dutygasturbine
r/min
1.2 转子动态响应计算
将离散后转子各段的质量、刚度和阻尼分别代入式(2)进行计算:
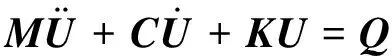
(2)
式中:M、C、K分别为转子的质量矩阵、阻尼矩阵和刚度矩阵;U为位移向量;Q为广义力向量,不包括滑动轴承油膜力。
(3)
由于该动态响应需施加于转子静力学分析模型来计算端面弧齿动应力,动力学分析模型与静力学分析模型相同(见图3)。
留守儿童是一个群体,是一个集合名词。在这个群体之中有明显的两类人,第一类孩子与大多数孩子无异,甚至在思想上要高于一般孩子,乐观坚强,关爱他人,常常苦中作乐,很容易被忽视;第二类孩子是心理自我疏导不够的孩子,性格内向,不善言谈,实际上他们也是向往童年肆意,天真烂漫的。基于这一了解,我就结合实际展开问题分析,尝试着探究原因,并提出策略。
鉴于转子结构复杂,且每个转子的质心不平衡量不同,计算偏心率时取动平衡后总的偏心率。根据该转子的现场测试结果,正常工作时透平端轴承的振幅为50 μm,由此反推得到转子的偏心率。基于滑动轴承刚度和阻尼的各向异性,各节点的轴心轨迹为椭圆。转子的工作转速为3 000 r/min,大于二阶临界转速,对于运动中的任一时刻,转子的动态响应为一空间曲线,如图4所示。
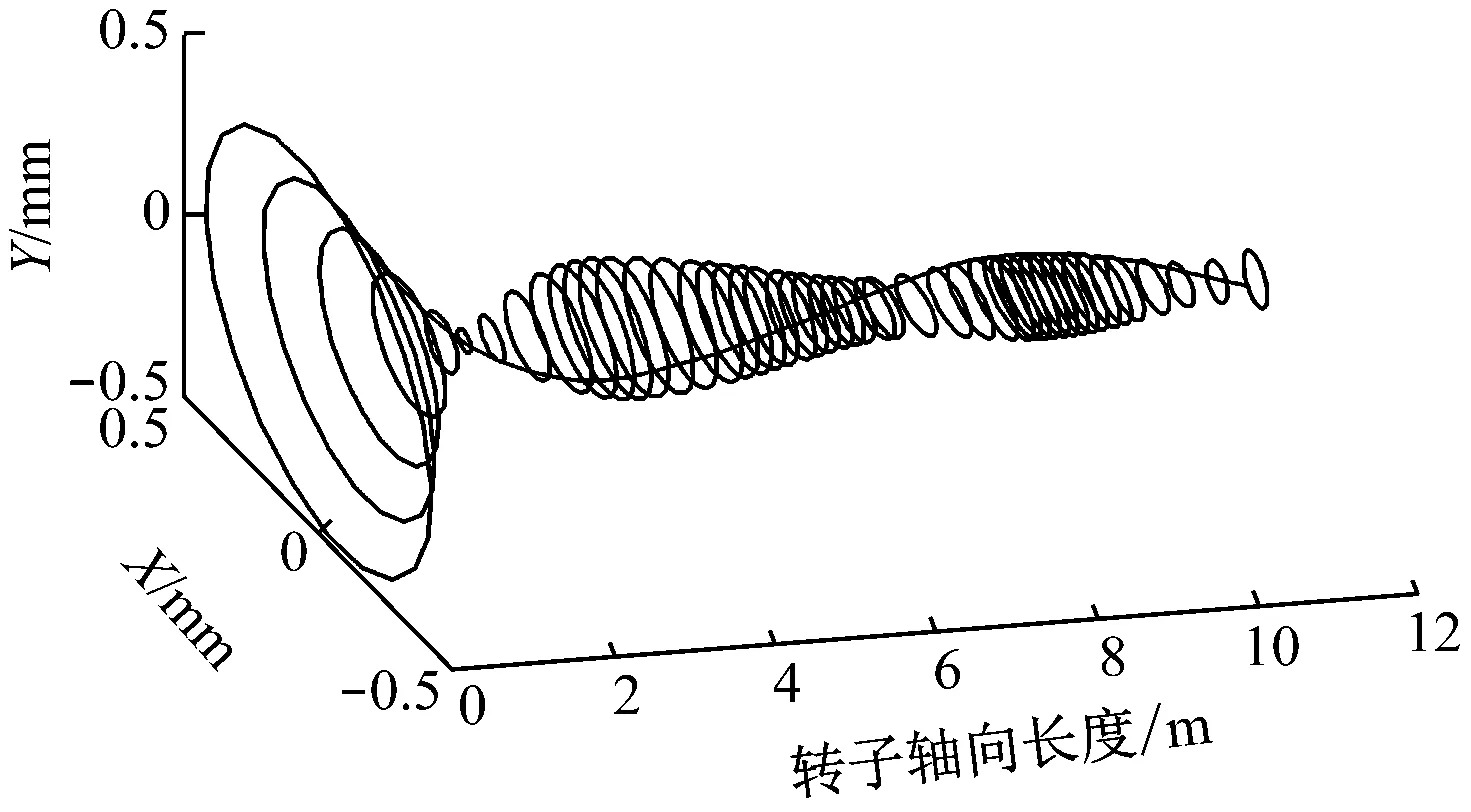
图4 转子正常工作时某一时刻的动态响应曲线
Fig.4 Dynamic response of the rotor at a given time under normal working condition
图5给出了透平1级轮盘的轴心轨迹,将1周的运动分成20个时间点,分别称为工作点1~工作点20,其他轮盘及轴段也根据该时间点提取对应的轴心位置,得到相应的动态响应曲线。
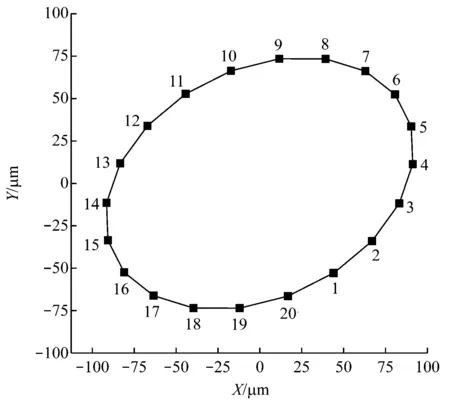
图5 转子正常工作时透平1级轮盘的轴心轨迹
Fig.5 Running orbit of disk 1 in turbine end under normal working condition
2 端面弧齿转子有限元模型
采用与动态响应分析相同的转子进行有限元分析,该转子透平端有4级轮盘,端面弧齿齿数为180,轮盘用12根周向拉杆联接。建立的转子有限元模型如图6所示,上方是端面弧齿网格的局部放大图,端面弧齿网格划分密度与文献[2]进行了对比,根据文献[2],当端面弧齿处网格达到图6的密度时,可以满足有限元计算精度。左上角为齿上一层节点的编号,在周向共分了37个节点。轮盘及拉杆材料特性见表2。模型边界条件根据工况设置。

图6 某重型燃气轮机转子有限元模型
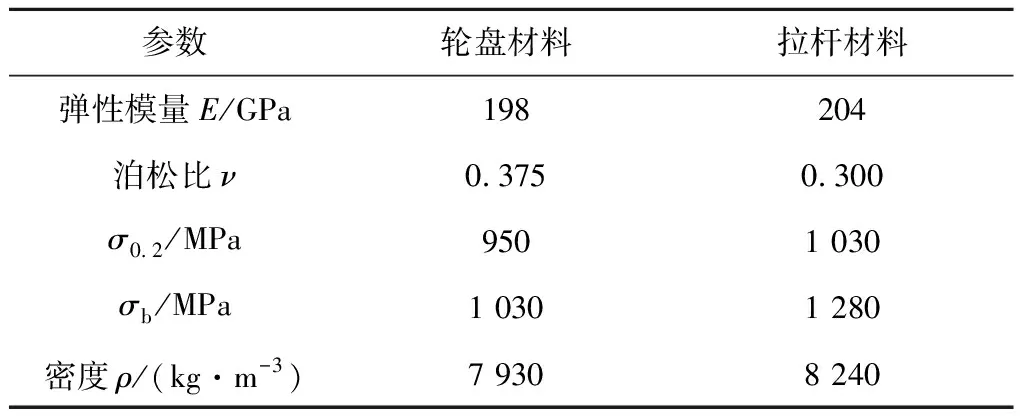
参数轮盘材料拉杆材料弹性模量E/GPa198204泊松比ν0.3750.300σ0.2/MPa9501 030σb/MPa1 0301 280密度ρ/(kg·m-3)7 9308 240
端面弧齿首先通过拉杆进行预紧,将各级轮盘联接在一起,即预紧工况;转子工作时承受离心力作用,称为离心力工况;燃气轮机做功需要传递扭矩,称为扭矩工况,扭矩力作用时端面弧齿两侧应力有所不同,分别称为承扭侧和非承扭侧;端面弧齿在动态弯曲力作用下的受力称为弯矩工况。预紧时对基准面的轴向位移进行限制,即对左侧(或右侧)端面施加轴向约束,采用PRETS179预紧单元对拉杆施加预紧力。离心力作为惯性载荷施加,将工作转速3 000 r/min对应的角速度314 rad/s施加于转子周向方向。施加扭矩时需对转子端部的周向位移进行限制,即对左侧端面施加周向约束。扭矩力通过对相应节点施加切向力实现,将各级轮盘功率通过式(4)换算成扭矩,扭矩与轮盘半径的比值即为该轮盘总的切向力大小,将该切向力平均分配到轮盘外径处各节点,作为周向力施加。施加弯曲力时,首先对转子进行节点划分(见图3),并采用式(2)分析转子在工作时的不平衡响应,得到相应的动态响应曲线,然后把该动态响应曲线代入Ansys有限元模型,即提取动力学分析模型中各节点的动态位移,加在Ansys有限元模型中相应的轴向位置。
(4)
式中:Ti为第i级轮盘的扭矩,N·m;Pi为第i级叶片的功率,W;N为转子工作转速,r/min。
3 结果与讨论
端面弧齿的每个接触对由凸齿和凹齿配合而成,各有180个齿,每个端面弧齿角度为1°,两齿间空余1°用于与另一轮盘的端面弧齿配合。以透平端接触对2为例进行研究,其他接触对与其类似。从0°开始对端面弧齿进行编号,如图7所示,图中也体现了各端面弧齿与拉杆的相对位置。
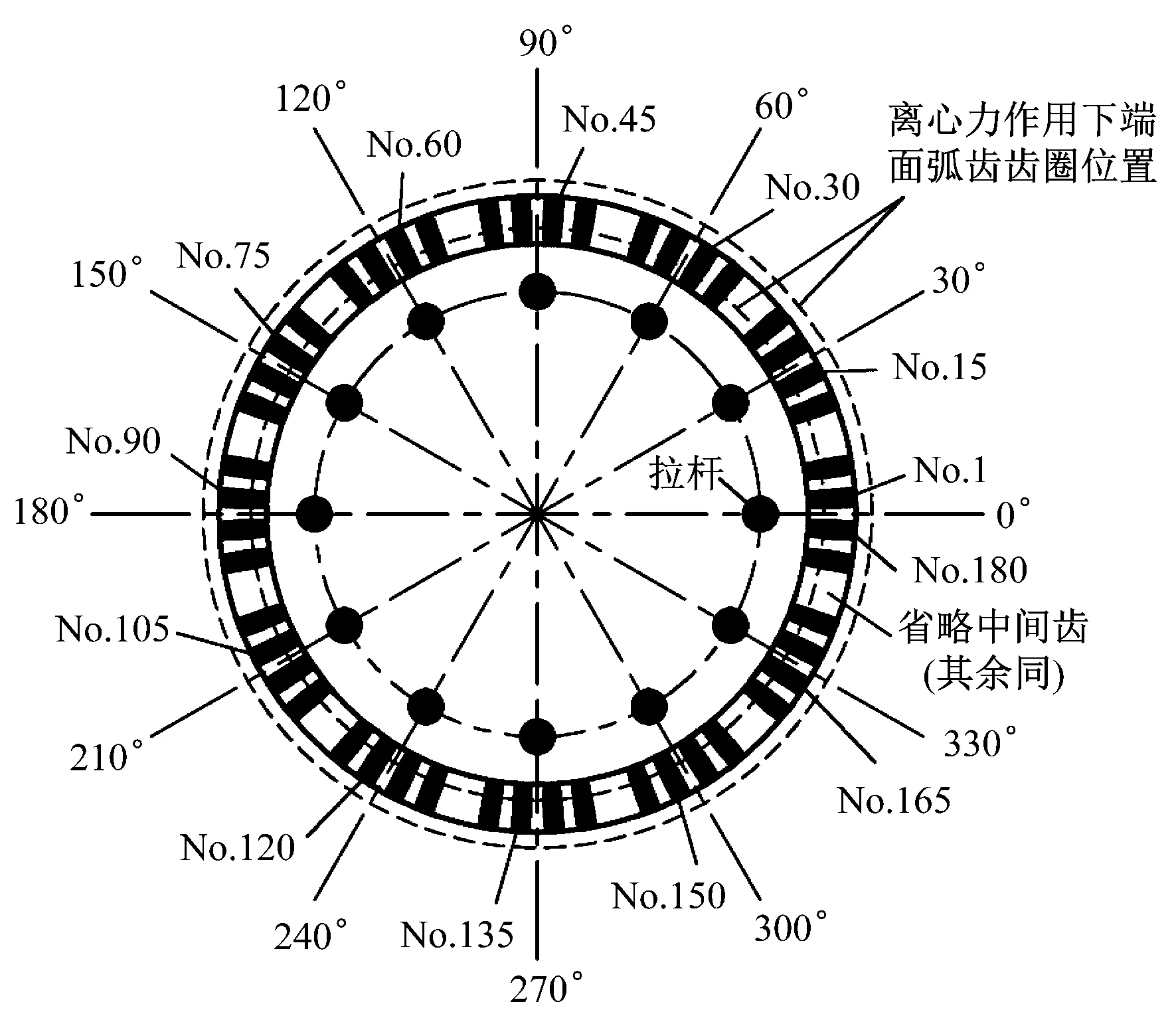
图7 端面弧齿编号
图8给出了端面弧齿在预紧力、离心力、扭矩力及动态弯曲力作用下的von Mises应力,该应力大小为接触面上各节点的平均应力。扭矩力作用下承扭侧与非承扭侧将产生明显的应力差,因此扭矩和弯矩作用下各有2条曲线,图8中S1代表承扭侧,S2代表非承扭侧。图9是No.120齿正应力和剪应力的变化直方图,X为径向,Y为周向,Z为轴向。柱坐标系下的三向正应力表示为SXX、SYY和SZZ,剪应力表示为SXY、SYZ和SXZ。为得到各齿详细的应力分布,将单个齿沿周向进行编号,每个齿分为37个节点,见图6左上角,从而可以得到各齿沿周向的应力分布情况。
3.1 预紧力的影响
从图8还可以看出,在预紧力作用下,12根离散拉杆所形成的应力局部化现象不明显,各齿应力相差不大。

图8 各工况下180个齿的应力状态
从图9可以看出,此时端面弧齿齿面应力主要表现为轴向和周向的正应力以及剪应力,而径向应力很小,可以忽略不计。通过计算,预紧后端面弧齿各应力分量的大小与压力角有关。对比压力角为30°和40°时单个齿的应力(见图10)可以看出,压力角越大,端面弧齿应力越小,其承扭能力越强。这是因为增大压力角使得齿根位置变宽,齿尖位置变窄,而端面弧齿的强度取决于齿根强度,齿根变宽,其强度增加。但当压力角过大时,周向力远远小于轴向力,扭矩作用下容易造成接触界面滑移,承担同样扭矩需施加很大的预紧力,因此压力角过大反而不利于承扭。而压力角减小也会导致接触界面应力分布不均。设计时应根据载荷选择合适的压力角,轻载时选择较小压力角,可使预紧力不必过大;重载时采用较大压力角,并增加预紧力来提高承扭能力。
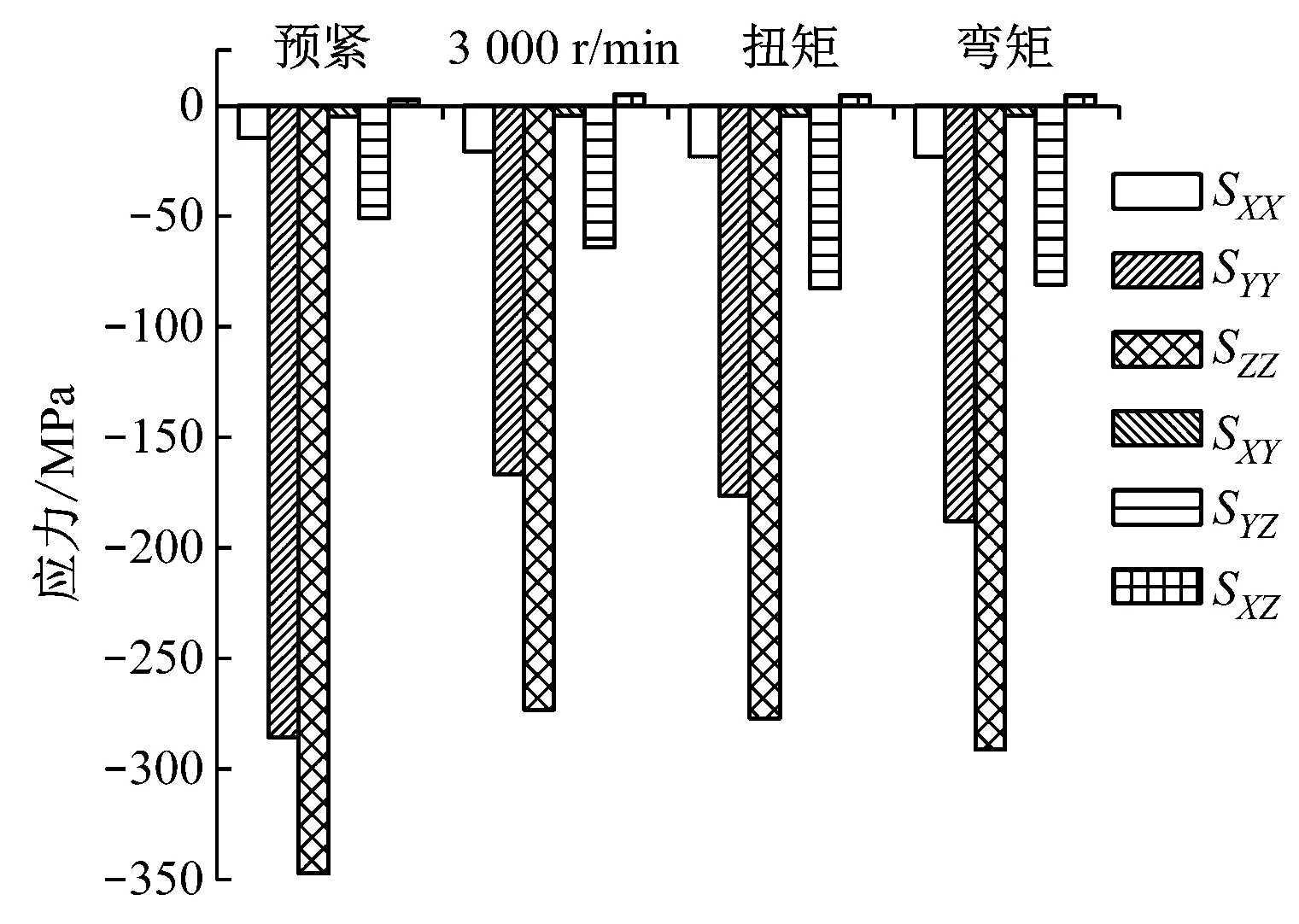
(a) 承扭侧

(b) 非承扭侧
Fig.9 Stress comparison under different working conditions of tooth No.120
Fig.10 Hoop stress and axial stress comparison for the teeth at different pressure angles
3.2 离心力的影响
图8中,离心力使端面弧齿应力减小,并导致各齿之间产生了明显的应力差,180个齿中表现出明显的波峰和波谷。结合图7可以看出,处于拉杆位置的端面弧齿齿面接触应力较小。齿面应力减小的原因在于轴向应力(SZZ)和周向应力(SYY)减小(见图9),离心力的作用使轮盘径向伸长,轴向由于泊松效应将缩短,因而接触应力SZZ减小。此外,轮盘径向伸长导致端面弧齿齿圈从图7中实线位置变到虚线位置,齿圈变大减小了径向挤压力,导致SYY减小。其次由于拉杆的存在,导致轮盘周向质量分布不再均匀,而是存在周期性变化。拉杆材料的密度较大,体积也大于各级轮盘去除材料的总和,总质量上,拉杆处大于其他齿处,质量较大的拉杆处在离心力作用下,径向变形更大,使SZZ和SYY减小更多,因而形成了图8所示的应力波动。该波动将一直存在于整个工作过程中。对于此类结构,拉杆引起的波动难以避免,只能尽可能减小而无法消除。在设计中选择与轮盘密度相同或密度小于轮盘的拉杆材料,或者适当增加拉杆数量可减小端面弧齿应力波动。图11为将拉杆数量增加一倍后的端面弧齿接触界面应力分布,此时拉杆造成的应力波动明显减小。
离心力可显著增大端面弧齿齿根应力,图12给出了预紧后和升速后正应力的对比。从图12可以看出,从预紧完成到升速至工作转速,齿根的径向应力和轴向应力基本保持不变,而周向应力显著增大。其原因仍可从齿圈位置的变化解释。
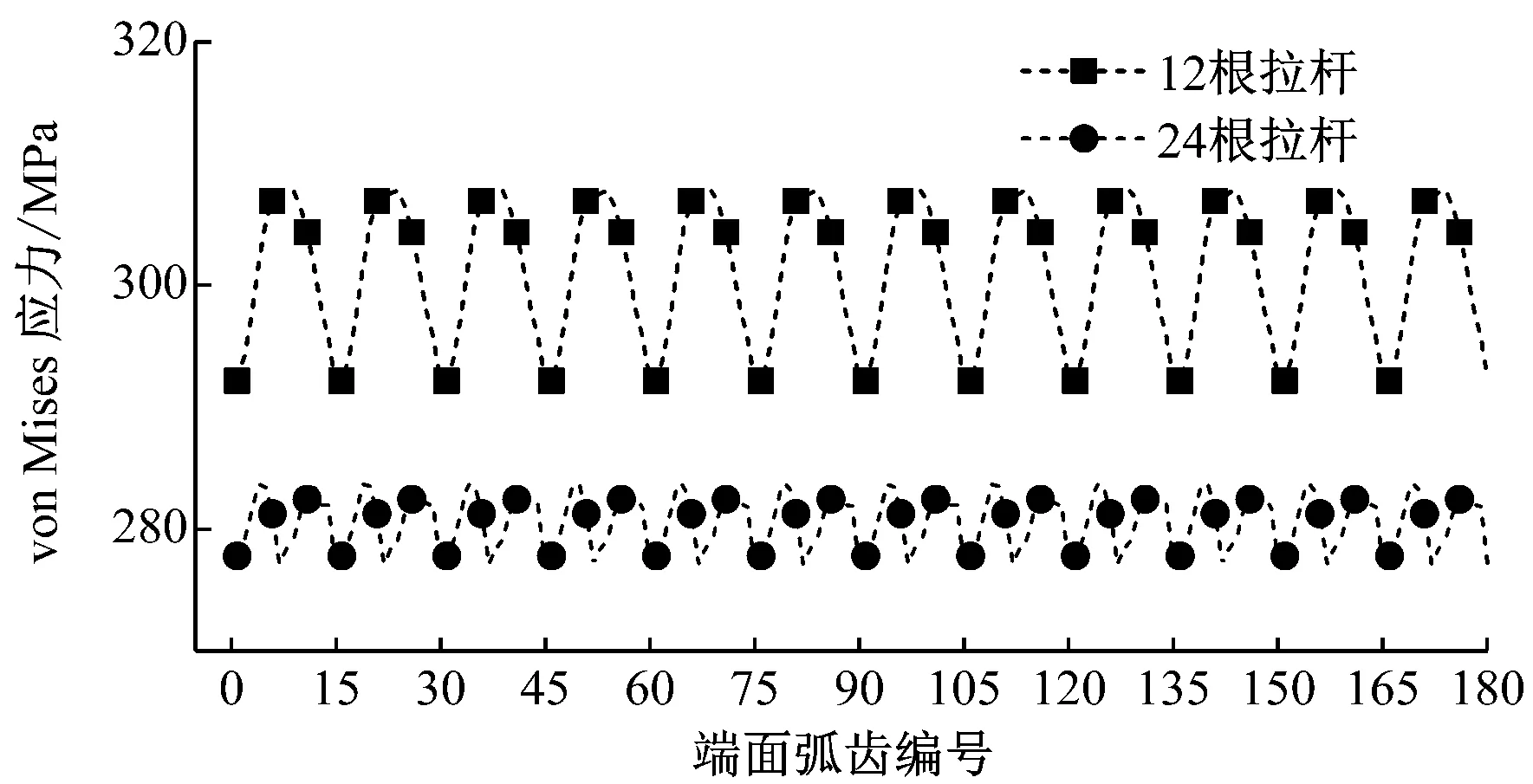
图11 拉杆数量不同时端面弧齿在3 000 r/min工作状态下的应力对比
Fig.11 Von Mises stress comparison between two rotors with different numbers of bolt under 3 000 r/min condition

图12 预紧后和升速后正应力的对比
Fig.12 Direct stress comparison between preload and 3 000 r/min conditions
预紧完成后,齿面的周向应力主要表现为压应力,而齿根主要表现为拉应力(正值表示拉伸,负值表示压缩),离心力作用下齿圈外移,使得原来大小的齿圈需进一步拉伸以适应新的位置,因此齿根的周向应力增大。齿根应力的增大与齿面应力的减小使得拉杆位置的端面弧齿受力状态尤为恶劣,是承载中的薄弱环节。
3.3 扭矩力的影响
图8中,扭矩力的作用使端面弧齿的承扭侧应力增大,非承扭侧应力减小。基本在离心力应力曲线的两侧对称分布。而对比图9(a)和图9(b)可以看出,扭矩力主要改变了YZ方向的剪应力SYZ,承扭侧的剪应力增大,非承扭侧剪应力减小,轴向应力基本不受扭矩力影响,周向应力由于承扭时的挤压作用而在承扭侧增大,但非承扭侧则基本不变。因此可以得出,端面弧齿主要是依靠YZ方向的剪切作用和承扭侧的周向挤压作用承扭,根据端面弧齿的承扭特点,设计上应选择抗剪能力强的材料,并经过优化计算选择合适的压力角使端面弧齿承扭能力达到最大。
3.4 动态弯曲力的影响
叠加了动态弯曲力后,由于转子的涡动使得拉杆稍有伸长,因此承扭侧和非承扭侧应力均有所增大。并且由于弯曲,180个齿的应力不再呈现周期对称性,各齿的应力状态随时间变化,这也造成了各齿的应力交变。由图8可知,正常工作时的弯曲力作用下,承扭侧应力增大了2%,非承扭侧应力增大了6%。尽管应力增大并不明显,但弯曲应力会导致周向各齿的应力不均,使转子刚度产生各向异性,增加轴心轨迹的椭圆程度,从而降低转子的稳定性。图13给出了不同位置端面弧齿在图5所示20个工作点的应力曲线。从图13可以看出,由于转子运动为一涡动过程,随着工作点的变化,转子的位置也发生相应变化,而由于支撑刚度的各向异性,转子轴心轨迹为椭圆,转子从椭圆的短轴运动到长轴的过程将产生应力交变,运动一周将产生2次交变。此外,同样处于拉杆位置的齿在弯曲力的作用下,会产生一定的应力差别。

图13 不同位置端面弧齿旋转一周的应力曲线
Fig.13 Von Mises stress comparison between teeth No.30 and No.90 in a round
4 结 论
(1) 端面弧齿的承扭能力与压力角有关,压力角越大,承扭能力越强,但压力角不应过大,否则会降低传递效率,反而不利于承载。
(2) 离心力作用下,端面弧齿应力出现了波动,处于拉杆位置的端面弧齿齿面应力较小,处于中间位置端面弧齿齿面应力较大,而齿根应力变化趋势则相反,因此拉杆位置端面弧齿是承载中的薄弱环节。在设计中应尽量选择与轮盘密度相同或密度小于轮盘的拉杆材料,或者适当增加拉杆数量以减小应力波动。
(3) 弯曲会破坏转子的周期性,受拉侧与受压侧产生了明显的应力差。由于转子轴心轨迹为椭圆,端面弧齿旋转一周将发生2次应力交变。
