汽轮机高温部件总寿命的计算方法及工程验证

史进渊

(上海发电设备成套设计研究院有限责任公司，上海 200240)

汽轮机的高温部件包括超高压模块、高压模块与中压模块的转子、内缸、外缸和阀壳等部件。在汽轮机起动、停机与负荷变动的瞬态工况下，由于力载荷和热载荷会引起低周疲劳作用，导致汽轮机高温部件的低周疲劳裂纹萌生及扩展。汽轮机在带负荷运行的稳态工况下，由于工作温度与力载荷引起的蠕变作用，导致汽轮机高温部件蠕变裂纹萌生与扩展。在汽轮机运行过程中，起动、停机与负荷变动等瞬态工况与带负荷运行的稳态工况交替出现，汽轮机高温部件交替发生低周疲劳与蠕变损伤，继而发生裂纹萌生与裂纹扩展。

汽轮机高温部件在低周疲劳与蠕变交互作用下的寿命计算涉及汽轮机的安全运行，国内外学者开展了一些研究工作。早在1969年，Timo[1]提出了汽轮机高温部件低周疲劳裂纹萌生寿命的计算方法。史进渊等[2]给出了汽轮机高温部件蠕变裂纹萌生寿命的计算方法。 1977年，Kumeno等[3]提出了汽轮机转子低周疲劳裂纹扩展寿命的计算方法。史进渊等[4]将汽轮机转子低周疲劳裂纹扩展寿命的计算方法应用于汽轮机焊接低压转子脆性断裂评定。 Swaminatha等[5]给出了汽轮机高中压转子蠕变裂纹扩展寿命的计算方法。汽轮机高温部件通常采用线性[6-7]和非线性寿命累积损伤模型[8]来评定低周疲劳与蠕变交互作用下的裂纹萌生寿命累积损耗，工程上在考虑蠕变断裂力学参量的基础上研究其低周疲劳与蠕变交互作用下的裂纹扩展寿命[9-11]。尽管研究人员对汽轮机高温部件在低周疲劳与蠕变交互作用下的寿命开展了研究，但由于影响这些部件寿命的因素众多，仍缺少合适的寿命计算方法可供使用。

汽轮机高温部件的寿命计算面临诸多技术难点：一是汽轮机材料的疲劳与断裂力学性能数据，大多是在某一温度下一维试棒(单轴)的对称疲劳循环试验结果，在不同温度下三维汽轮机高温部件的寿命计算涉及非对称疲劳循环和多轴疲劳寿命建模；二是低周疲劳裂纹萌生寿命与裂纹扩展寿命的单位是疲劳循环次数，而蠕变裂纹的萌生寿命与扩展寿命的单位是运行小时数，电站用户希望采用年数来表示汽轮机高温部件的日历寿命；三是同时考虑汽轮机高温部件在低周疲劳与蠕变交互作用下裂纹萌生与裂纹扩展的日历总寿命的设计和评定，还没有合适的方法可供使用；四是汽轮机高温部件的寿命计算值很难通过电站的使用实践来进行工程验证。

国内620 ℃的一次再热与二次再热汽轮机已经投入运行，伴随着汽轮机进汽温度的不断提高，高温部件的材料强度已接近使用极限。电站业主对汽轮机的寿命要求不断提高，火电机组已经从30 a提高到40 a，核电机组已从40 a提高到60 a。电力行业提出的汽轮机快速起动、快速负荷变动、常态化深度调峰或两班制运行等新的灵活性要求，导致汽轮机寿命损伤大，影响其安全性。笔者针对汽轮机的高参数、长寿命和运行灵活性，研究了汽轮机高温部件在低周疲劳与蠕变交互作用下总寿命计算方法并进行工程验证，对于保障汽轮机的安全运行是一项重要的工作。

1 裂纹萌生寿命的计算方法

工程上，把长度为0.3～0.5 mm、深度为0.1～0.15 mm的裂纹称为工程裂纹，也称初始裂纹或宏观裂纹。裂纹萌生寿命指的是在某种或某几种损伤机理的作用下，从汽轮机高温部件首次投入运行到部件出现第一条工程裂纹的运行时间或疲劳循环次数，即出现工程裂纹的寿命。汽轮机高温部件的主要损伤机理是低周疲劳和蠕变，因此需要计算低周疲劳裂纹萌生寿命和蠕变裂纹萌生寿命。

1.1 低周疲劳裂纹萌生寿命

汽轮机高温部件的低周疲劳裂纹萌生寿命的预测属于多轴疲劳问题，采用最大瞬态应变和最小瞬态应变的非对称循环法[12]来计算。研究多轴疲劳理论的目标是根据材料单轴对称疲劳循环的试验数据曲线，预测复杂加载条件下汽轮机高温部件三维结构多轴应力状态的非对称疲劳循环的低周疲劳裂纹萌生寿命。

1.1.1 确定带有正号或负号的等效应变

采用有限元分析方法计算汽轮机高温部件在起动、停机或负荷变动等过程的瞬态应力场，根据von Mises公式计算得出的等效应变εeq为正值，而汽轮机高温部件低周疲劳循环的最大主应变εmax和最小主应变εmin均有可能是正值、负值或零。在构建汽轮机高温部件非对称低周疲劳循环的寿命计算模型时，就需要确定等效应变的正负号。根据文献[13]～文献[14]，采用sign(ε1+ε3)识别等效应变的正负号。带有正号或负号的等效应变εei计算公式为

sign(ε1+ε3)=εeqsign(ε1+ε3)

(1)

式中：sign(x)为符号函数，若x>0，则sign(x)=1,若x<0，则sign(x)=-1;i=1,2,…,m。

1.1.2 计算低周疲劳裂纹萌生的应变幅

将汽轮机的一次冷态起动与一次滑参数停机构成一个低周疲劳循环，一次温态起动与一次正常停机构成一个低周疲劳循环，一次热态起动与一次正常停机构成一个低周疲劳循环，一次极热态起动与一次事故停机构成一个低周疲劳循环，一次大的升负荷(25%升至75%～100%)与一次大的降负荷(75%～100%降至25%)构成一个大负荷变动的低周疲劳循环，一次小的升负荷(50%至75%～100%)与一次小的降负荷(75%～100%降至50%)构成一个小的负荷变动的低周疲劳循环。汽轮机高温部件的起停低周疲劳循环和负荷变动低周疲劳循环属于非对称循环，在汽轮机高温部件的一个低周疲劳循环中，εmax和εmin的计算公式分别为

εmax=max{εe1,εe2,…,εei,…,εem}

(2)

εmin=min{εe1,εe2,…,εei,…,εem}

(3)

假定不同的起动、负荷变动或停机过程中εmax和εmin的方向相同，采用εei来计算汽轮机高温部件的低周疲劳循环应变幅εa，其计算公式为

(4)

式中:Δε为疲劳循环的应变范围或全应变。

1.1.3 计算循环的等效应变幅

考虑材料缺口敏感性、低周疲劳循环不对称性、高周疲劳和高温持久强度等影响因素修正后，汽轮机高温部件非对称低周疲劳循环的等效应变幅εaeq的计算公式为

(5)

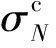
1.1.4 确定低周疲劳裂纹萌生寿命

根据疲劳循环的等效应变幅εaeq查材料低周疲劳裂纹萌生寿命曲线εai=f(Ni)，可确定汽轮机高温部件的非对称低周疲劳循环次数Ni，即低周疲劳裂纹萌生寿命。

1.2 蠕变裂纹萌生寿命

根据文献[2]和文献[12]，采用稳定蠕变应力与拉森-米勒参数(Larson-Miller Parameter)的外推法计算汽轮机高温部件蠕变裂纹萌生寿命。

1.2.1 确定材料持久强度曲线

汽轮机高温部件材料持久强度στ的拉森-米勒参数可表示为试验温度T和断裂时间tr的函数：

T(C+lgtr)=A0+A1lgστ+A2lg2στ+A3lg3στ+

A4lg4στ+A5lg5στ

(6)

tr=10x

(7)

(8)

式中:στ为对应于断裂时间tr的材料持久强度；C为材料常数；A1、A2、A3、A4和A5为材料试验常数。

1.2.2 确定稳定蠕变应力对应的材料断裂时间tr

采用有限元分析方法确定汽轮机高温部件的稳态温度场和稳定蠕变等效应力σc，利用汽轮机高温部件的σc和工作温度T0，根据式(6)，可确定σc对应的材料断裂时间tr。

1.2.3 计算蠕变裂纹萌生寿命

根据文献[2]和文献[12]确定安全系数nt，汽轮机高温部件蠕变裂纹萌生寿命τic的计算公式为

(9)

2 裂纹扩展寿命的计算方法

在某种或某几种损伤机理的作用下，从工程裂纹扩展到可能发生断裂的临界裂纹尺寸(或具体裂纹尺寸)所经历的运行时间或疲劳循环次数称为裂纹扩展寿命。汽轮机高温部件的裂纹扩展寿命主要包括低周疲劳裂纹扩展寿命和蠕变裂纹扩展寿命。

2.1 低周疲劳裂纹扩展寿命

对于汽轮机高温部件，采用最大主应力与断裂力学的方法计算低周疲劳裂纹扩展寿命。

2.1.1 计算最大应力和应力范围

建立汽轮机高温部件的三维有限元模型，加载汽轮机起动、停机、负荷变动或超速试验等瞬态过程的热载荷与力载荷，可计算出汽轮机瞬态工况下不同时刻汽轮机高温部件的瞬态温度场和应力场。通过对汽轮机高温部件瞬态应力场的分析，可以确定汽轮机瞬态工况的最大主应力σ1max。通常汽缸与阀壳的外表面以及转子内表面与转子内部的最大拉应力出现在汽轮机的起动过程中，汽缸与阀壳的内表面以及转子外表面的最大拉应力出现在汽轮机停机过程中。汽轮机高温部件低周疲劳裂纹扩展的最大应力σmaxL的计算公式为

σmaxL=σ1max+σre

(10)

式中：σre为汽轮机高温部件的残余应力；实际上最大主应力σ1max与σre的方向并不相同，寿命计算中假定σ1max与σre的方向相同，计算结果偏于安全[15]。

考虑到汽轮机停机时部件的应力为零，即低周疲劳裂纹扩展的最小应力σminL=0，汽轮机高温部件低周疲劳裂纹扩展的应力范围ΔσL的计算公式为

ΔσL=σmaxL-σminL=σmaxL

(11)

2.1.2 计算低周疲劳临界裂纹尺寸

根据文献[16]，汽轮机高温部件低周疲劳临界裂纹尺寸acL的计算公式为

(12)

式中:KIC为材料的断裂韧性；M为根据文献[3]和文献[12]确定的与裂纹部位和椭圆形裂纹形状参数有关的常数。

2.1.3 计算低周疲劳裂纹扩展寿命

低周疲劳裂纹扩展寿命Np的计算公式为

(13)

式中:ai为工程裂纹深度，在制造与使用阶段，可依据实际裂纹的探伤数值确定，此处取ai=0.1 mm；C0、m0为低周疲劳裂纹扩展的材料试验常数[12]。

2.2 蠕变裂纹扩展寿命

对于汽轮机高温部件，采用稳定蠕变最大主应力与断裂力学的方法计算蠕变裂纹扩展寿命。

2.2.1 计算稳定蠕变最大应力

通过建立汽轮机高温部件的三维有限元模型，加载汽轮机设计工况热载荷与力载荷，可计算得出汽轮机设计额定工况下高温部件的稳态温度场和稳定蠕变最大主应力σ1c。汽轮机高温部件蠕变裂纹扩展的稳定蠕变最大应力σmaxc的计算公式为

σmaxc=σ1c+σre

(14)

2.2.2 计算蠕变临界裂纹尺寸

汽轮机高温部件蠕变临界裂纹尺寸acc为

(15)

2.2.3 计算蠕变裂纹扩展寿命

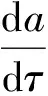
(16)

C*=Aa

(17)

(18)

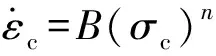
在汽轮机的带负荷稳态运行过程中，推导汽轮机高温部件从初始裂纹ai至蠕变临界裂纹尺寸acc的蠕变裂纹扩展寿命τpc计算式：

(19)

(20)

当m4<1时，

(21)

当m4=1时，

(22)

当m4>1时，

(23)

3 日历寿命的计算方法

汽轮机高温部件的裂纹萌生寿命和裂纹扩展寿命可以采用日历年数表示为日历寿命，此时的裂纹萌生寿命称为裂纹萌生日历寿命，裂纹扩展寿命称为裂纹扩展日历寿命。

3.1 裂纹萌生日历寿命

对于变幅载荷汽轮机高温部件，在裂纹萌生阶段，考虑到拉应力与压应力、正应变与负应变均可引起裂纹萌生，假定带负荷运行稳态工况以及不同瞬态工况下的最大应变与最小应变的方向相同，应用Palmgern-Miner寿命损耗线性叠加法则[17-18]，计算汽轮机高温部件的裂纹萌生日历寿命。

3.1.1 汽缸与阀壳

对于汽轮机的汽缸、阀壳等静止高温部件，针对汽轮机不同的起动、停机、负荷变动等瞬态工况以及带负荷运行稳态工况，在计算得出低周疲劳裂纹萌生寿命与蠕变裂纹萌生寿命后，这些高温部件的裂纹萌生寿命累积损耗Ei、年均寿命损耗eyi和裂纹萌生日历寿命τCLi的计算公式分别为

(24)

(25)

(26)

式中:D为小于等于1的寿命损伤系数；n为实际起动或停机的次数；y为年均次数；下标c表示冷态起动，w表示温态起动，h表示热态起动,r表示极热态起动,1表示大负荷变动,2表示小负荷变动；tSH为实际运行小时数；ty为年均运行小时数。

3.1.2 转子

对于汽轮机的转子等转动高温部件，除了要考虑汽轮机不同的起动、停机、负荷变动等瞬态工况以及带负荷运行稳态工况外，还要考虑汽轮机超速试验的瞬态工况，在计算得出低周疲劳裂纹萌生寿命与蠕变裂纹萌生寿命后，汽轮机高中压转子的裂纹萌生寿命累积损耗Ei、年均寿命损耗eyi和裂纹萌生日历寿命τCLi的计算公式分别为

(27)

(28)

(29)

其中，下标110、120分别表示110%超速试验过程和120%超速试验过程。

3.2 裂纹扩展日历寿命

在汽轮机高温部件的裂纹扩展阶段，汽轮机带负荷运行稳态工况发生蠕变裂纹扩展，汽轮机起动、停机、负荷变动或转子超速试验过程等瞬态工况发生低周疲劳裂纹扩展。考虑到压应力不会引起裂纹扩展，只有拉应力才会引起裂纹扩展，对于汽缸与阀壳的外表面以及转子内部，通常在起动过程与负荷变动升负荷过程中出现最大主应力，发生低周疲劳裂纹扩展；对于汽缸与阀壳的内表面以及转子外表面，通常在停机过程与负荷变动降负荷过程中出现最大主应力，发生低周疲劳裂纹扩展；对于汽轮机转子，还要考虑汽轮机110%超速试验过程以及120%超速运行的低周疲劳裂纹扩展；对于变幅载荷的汽轮机高温部件，在裂纹扩展阶段，假定不同的起动、停机、负荷变动或超速试验等瞬态工况以及带负荷运行稳态工况的最大主应力的方向相同，同样应用Palmgern-Miner寿命损耗线性叠加法则[17-18]，计算汽轮机高温部件的裂纹扩展日历寿命。

3.2.1 汽缸与阀壳的外表面

对于汽轮机高中压汽缸与阀壳的外表面，在起动与负荷变动升负荷的瞬态工况出现最大应力引起的低周疲劳裂纹扩展，带负荷运行稳态工况稳定蠕变最大应力导致裂纹蠕变扩展。高中压汽缸与阀壳的外表面的裂纹扩展寿命累积损耗Ep、年均寿命损耗eyp和裂纹扩展日历寿命τCLp的计算式分别为

(30)

(31)

(32)

3.2.2 汽缸与阀壳的内表面

对于汽轮机高中压汽缸与阀壳的内表面，在停机与负荷变动降负荷的瞬态工况出现最大主应力，引起低周疲劳裂纹扩展，带负荷运行的稳态工况导致裂纹蠕变扩展。高中压汽缸与阀壳的内表面的裂纹扩展寿命累积损耗Ep、年均寿命损耗eyp和裂纹扩展日历寿命τCLp的计算公式分别为

(33)

(34)

(35)

式中:下标s表示滑参数停机，n表示正常停机，e表示事故停机。

3.2.3 转子外表面

对于汽轮机高中压转子外表面，在停机、负荷变动降负荷、110%以及120%超速试验的瞬态工况出现最大主应力，引起低周疲劳裂纹扩展，带负荷运行的稳态工况导致裂纹蠕变扩展。汽轮机高中压转子外表面的裂纹扩展寿命累积损耗Ep、年均寿命损耗eyp和裂纹扩展日历寿命τCLp的计算公式分别为

(36)

(37)

(38)

3.2.4 转子内部

对于汽轮机高中压转子内部，在起动、负荷变动升负荷、110%以及120%超速试验的瞬态工况出现最大主应力，引起低周疲劳裂纹扩展，带负荷运行的稳态工况导致裂纹蠕变扩展。汽轮机高中压转子内部的裂纹扩展寿命累积损耗Ep、年均寿命损耗eyp和裂纹扩展日历寿命τCLp的计算公式分别为

(39)

(40)

(41)

4 总寿命的设计与评定方法

在低周疲劳和蠕变的交互作用下，从汽轮机高温部件首次投入运行到可能发生断裂的临界裂纹尺寸(或具体裂纹尺寸)为止，高温部件所经历的运行时间与疲劳循环次数称为总寿命。汽轮机高温部件总寿命由裂纹萌生寿命和裂纹扩展寿命两部分构成，也称为全寿命或致断寿命，以日历年数表示的总寿命称为日历总寿命。

4.1 总寿命的计算方法

在低周疲劳与蠕变交互作用下，汽轮机高温部件的总寿命损耗Et、日历总寿命τCLt分别为

Et=Ei+Ep

(42)

τCLt=τCLi+τCLp

(43)

4.2 总寿命的评定方法

在汽轮机高温部件的设计阶段，用Y0表示电站业主要求的使用寿命年数，汽轮机高温部件τCLt的安全性评定判据如下：

(1)若τCLi+τCLp≥Y0，在低周疲劳与蠕变交互作用下，汽轮机高温部件日历总寿命的设计是安全的。

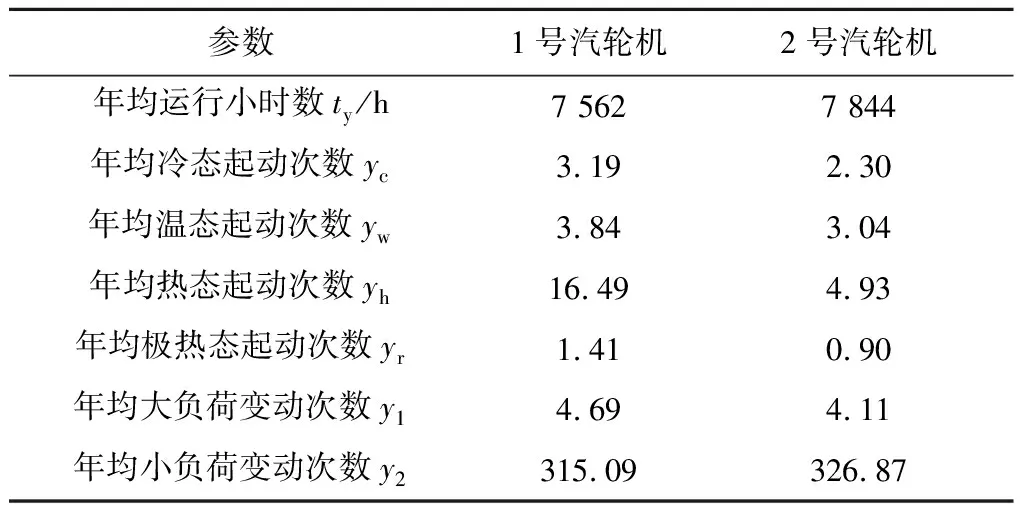
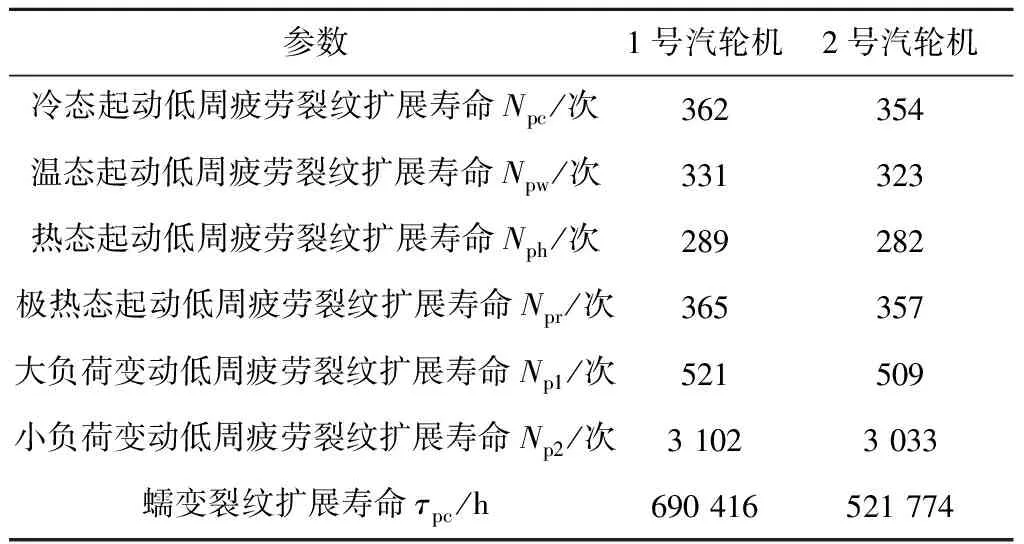
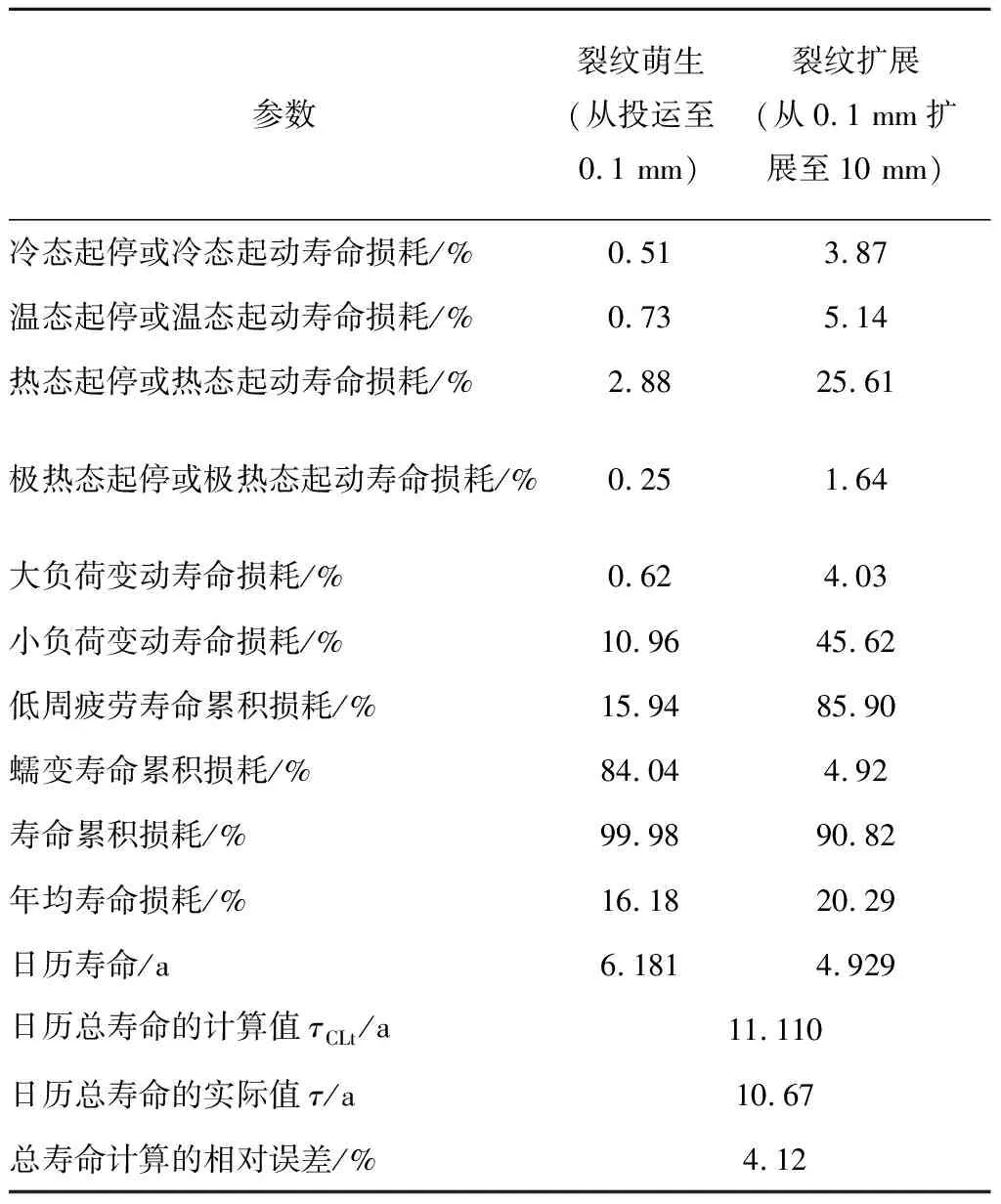
(2)若τCLi+τCLp

4.3 剩余日历寿命的计算方法

汽轮机高温部件从首次并网投入运行日至剩余寿命评估日之间的日历年数称为日历寿命的实际值，用符号τ表示。汽轮机高温部件的剩余寿命百分数ERL和剩余日历寿命τRL的预测公式分别为

ERL=(D+1)-(Ei+Ep)

(44)

τRL=(τCLi+τCLp)-τ

(45)

4.4 剩余日历寿命的评定方法

在汽轮机高温部件的使用阶段，汽轮机高温部件剩余日历寿命的安全性评定判据如下：

(1)若τRL≥(Y0-τ)，在低周疲劳与蠕变交互作用下，汽轮机高温部件剩余日历寿命是安全的。

(2)若τRL<(Y0-τ)，在低周疲劳与蠕变交互作用下，汽轮机高温部件剩余日历寿命是不安全的。

5 工程验证实例

5.1 工程实例

某电厂2台超临界600 MW汽轮机高压内缸的结构如图1所示，该高压内缸的寿命薄弱部位是该内缸外表面的部位P。该电厂1号汽轮机运行10.67 a，在大修中发现P处有整圈裂纹，裂纹深度为10 mm。该电厂2号汽轮机运行12.17 a，在大修中发现其P处也有整圈裂纹，裂纹深度为5 mm。

图1 某超临界600 MW汽轮机高压内缸的示意图

这2台超临界汽轮机从首次并网至大修发现裂纹期间的实际运行小时数、实际起动次数与实际大负荷变动次数见表1。由于缺少这2台汽轮机的小负荷变动次数统计结果，在表1中，按照实际运行小时数除以24 h来确定小负荷变动次数。2台超临界汽轮机的年均运行小时数、年均起动次数与年均负荷变动次数的计算结果见表2。

应用本文方法，计算得出该高压内缸的裂纹萌生寿命(见表3)、1号汽轮机高压内缸P处从0.1 mm到10 mm的裂纹扩展寿命的计算结果以及2号汽轮机高压内缸P处从0.1 mm到5 mm的裂纹扩展寿命(见表4)。

表1 运行数据

表2 年均数据的计算结果

表3 变幅载荷裂纹萌生寿命的计算结果

表4 变幅载荷裂纹扩展寿命的计算结果

根据表2～表4的数据，给定D=1，代入式(26)和式(32)，得出1号汽轮机高压内缸裂纹萌生日历寿命和裂纹扩展日历寿命的计算结果分别为τCLi=6.181 a，τCLp=4.929 a。采用同样方法，计算得到2号汽轮机高压内缸τCLi=6.115 a，τCLp=5.996 a。

为了分析这2台汽轮机高压内缸裂纹萌生与裂纹扩展的寿命累积损耗，定义裂纹萌生所占寿命累积损耗的百分比x，x=τCLi/τ。对于1号汽轮机，x=57.9%；对于2号汽轮机，x=50.2%。由x可以得出这2台汽轮机裂纹萌生的运行小时数、不同类型起动次数与负荷变动次数的推算结果(见表5)，在表5中zi为运行数据的统计值。

依据表2～表5的数据，计算得出这2台汽轮机高压内缸的裂纹萌生与裂纹扩展的低周疲劳寿命累积损耗、蠕变寿命累积损耗、总寿命累积损耗以及年均寿命损耗、日历寿命、日历总寿命(见表6和表7)。

5.2 分析与讨论

从表6和表7可以看出，2台汽轮机高压内缸外表面寿命薄弱部位P的裂纹萌生寿命累积损耗分别达到99.98%和99.92%时裂纹萌生；1号汽轮机高压内缸外表面寿命薄弱部位P的裂纹扩展寿命累积损耗Ep1达到90.82%时裂纹扩展到10 mm；2号汽轮机高压内缸外表面寿命薄弱部位P的裂纹扩展寿命累积损耗Ep2达到100.90%时扩展到5 mm。

对于高压内缸的部位P，1号汽轮机与2号汽轮机的裂纹萌生蠕变寿命累积损耗分别为84.04%和86.21%，裂纹扩展的低周疲劳寿命累积损耗分别为85.90%和91.79%，表明这2台汽轮机高压内缸的裂纹萌生的主要损伤模式是蠕变，裂纹扩展的主要损伤模式是低周疲劳。

表5 运行小时数与起动次数的推算结果

表6 1号汽轮机寿命累积损耗与日历寿命计算结果

1号汽轮机高压内缸外表面寿命薄弱部位P的日历总寿命计算的相对误差为4.12%，2号汽轮机则为-0.48%。验证结果表明，本文的汽轮机高温部件总寿命的计算精度高，计算结果符合电站服役的工程实际。而这2台汽轮机高压内缸日历总寿命计算相对误差的差异，可能与缺少统计数据的2种近似处理有关：一是在本文计算日历寿命的方法中，实际上是把不同类型的起动次数或停机次数与负荷变动次数随着运行小时数的变化规律近似处理为线性变化；二是验证实例在缺少小负荷变动次数统计结果的情况下，通过实际运行小时数来近似确定实际小负荷变动次数。

表7 2号汽轮机寿命累积损耗与日历寿命计算结果

这2台汽轮机高压内缸的结构设计与材料牌号完全相同，只是实际运行小时数、起动次数有差异。通过2台汽轮机高压内缸的裂纹深度和日历寿命的实际值的工程验证，结果表明所采用的寿命计算方法是合适的，工程上是实用的。

众所周知，采用传统方法计算汽轮机高温部件寿命时，计算值与实际值相差两倍，寿命计算值可能是寿命实际值的一半或两倍，误差较大。由文献[19]可知，国外有一些设计规范中，对于低周疲劳裂纹萌生寿命，美国ASME压力容器采用等效应变幅计算得出疲劳循环次数的安全系数取为2，德国TRD301中疲劳循环次数的安全系数取为2。寿命计算取安全系数为2，目的是保证寿命计算结果有一定的安全裕度。由于寿命计算误差大，传统方法需要取2倍的安全系数来保证安全裕度。本文给出的汽轮机高温部件寿命计算方法，经工程验证，计算精度高。

6 结 论

(1)所提出的汽轮机高温部件在低周疲劳与蠕变交互作用下的寿命计算方法，考虑了汽轮机起停等瞬态工况引起低周疲劳和汽轮机带负荷运行稳态工况引起蠕变的2种损伤机理，实现了高温部件在低周疲劳与蠕变交互作用下裂纹萌生寿命、裂纹扩展寿命、日历寿命与总寿命的计算分析，为汽轮机高温部件的定寿与延寿提供了理论和技术依据。

(2)通过2台超临界600 MW汽轮机高压内缸在低周疲劳与蠕变交互作用下总寿命的计算分析与电站运行数据的工程验证，1号汽轮机高压内缸总寿命计算的相对误差为4.12%，2号汽轮机高压内缸总寿命计算的相对误差为-0.48%。验证结果表明，这2台汽轮机高压内缸的总寿命计算精度高，计算结果符合电站服役的工程实际。

(3)这2台600 MW汽轮机高压内缸的结构设计与材料牌号相同，只是实际运行小时数与起动次数有一些差异，高压内缸总寿命的计算结果符合电站服役的工程实际，表明本文计算方法以及有关参数的取值是合适的，工程上是实用的。