变点问题统计分析框架及应用——以我国财险赔付支出数据为例

(天津财经大学 统计学院，天津 300222)

一、引言

变点问题(Change Point Problem)自20世纪70年代以来一直是国际统计研究的热点，始于Page于1954年在Biometrika上发表的一篇关于连续抽样检验的文章，其主要研究时间序列过程中，在某个或几个未知时刻序列过程的统计特性产生变化，使得其不再依循于原有规律，所对应t时刻的点即为变点，通过对于变点的识别、估计，分析估计量在t时刻前后的差异及性质，对变量进行更合理的推断[1]。变点问题在风险识别和异常点监控中具有重要作用，其理论已有了一系列较为成熟的成果并有着较为广泛的应用，早期用于质量控制，后来扩展到医学、气象学、生物学、金融保险等诸多领域。

经济金融中的数据通常呈结构性或周期性变化，显然不能将之等量其观，其特定时期内的变化差异往往是研究问题的关键所在。随着金融业的蓬勃发展，变点问题在金融领域的研究受到了学者的广泛关注。在股票证券市场，变点分析侧重于时间序列建模：Kokoszka和Leipus构建了变点ARCH模型，Na等则建立了Copula-ARMA-GARCH模型测度了风险变点间的相依关系[2-3]。保险市场中，更关注于生存分析与损失模型的构建：Gandy等通过一组精算变点数据构建了Cox风险模型[4]，Jensen和Lütkebohmert则推广了Cox变点模型的应用范围，将其应用在不同协变量的变点以及单个变点的多个协变量中[5]。近几年来，金融变点研究侧重于累加和(Cumulative Sum，CUSUM)算法等传统识别方法的拓展以及贝叶斯统计方法的综合应用，数据由低维数据转向高维，关注方向也由变点定量识别转向变点的稳健性识别。Jirak基于高维时序数据间的弱相关性，结合CUSUM与自助法(Bootstrap)构建了一种大样本条件下的高维数据变点检验法，并据此识别了近一年内美国500家上市公司标准普尔指数(S&P500)的序列变点[6]。Cho和Fryzlewicz则根据CUSUM提出了一个稀疏化二值分割(Sparsified Binary Segmentation，SBS)算法用于减少高维空间中的无关噪声影响，利用该算法识别了2007—2011年中S&P500的变点，指出2008年美国金融危机前后该指数的结构性变化[7]。随后，Cho又将CUSUM应用于面板数据中多变点情形下的检测，分析了2015—2016年S&P100收益率的变化情况[8]。Nascimento和Silva提出一种多变点情况下的贝叶斯模型，运用MCMC算法对每个点的突变概率进行稳健估计，以美国纳斯达克(Nasdaq)数据为例识别了1996—2014年中的证券交易变点[9]。随着金融数据结构的日趋复杂，变点问题在国外的金融领域研究中无论是从对象上还是方法上都有了大幅扩展，具有非常广阔的发展空间和应用价值。

我国于上世纪90年代展开对变点问题的研究，陈希孺首次从国外引入提出变点问题[10]，此后国内学者展开了一系列理论研究。2000年后对于变点问题的应用研究增多，金融领域中变点问题在证券市场应用较为广泛。雷鸣等将生存分析与变点理论相结合，对我国上证指数进行研究，分析股市的政策效应变化[11]。谭常春等对至多一个变点的伽马分布进行了统计推断并在金融序列中进行了应用[12]。叶五一和缪柏其利用Copula的变点检测方法来检验美国次级债金融危机传染效应的存在性，分析了收益率间的相依关系[13]。李强和王黎明将变点估计问题转化成变量选择问题来处理，提出了一种基于LAD-LASSO的逐段常数时间序列变点估计方法[14]。在保险研究中，李云霞和周杏杏考虑保险精算中复发事件数据的重要作用，建立了含有协变量的复发事件变点模型[15]。刘琮敏等根据Poisson分布单变点的思想，运用鞅方法研究了具有变点理赔过程的风险模型，将变点模型应用于破产概率分析[16]。张志强和杨帆利用变点检测法识别了我国人口死亡率的突变点，用主成分分析构建模型提高了死亡率预测模型的精度[17]。整体上看，变点理论在金融领域的实证应用仍较为匮乏，涉及的重要风险变点尚未进行系统性的讨论，亟待学者展开相关研究来完善各类金融指标中重大风险点的识别工作，健全我国的金融风险管理体系。

本文尝试在前人研究的基础上构建一种变点问题的统计研究分析框架，从定量和定性两个视角确定金融问题中的关键风险点，通过变点前后差异构建不同的数据模型，以期揭示变点数据的内在规律性特征。以我国近7年来的赔付支出数据为例阐述变点问题的研究过程，着手从技术层面识别我国财险公司一年经营中赔付支出突变的关键月度风险点，对理赔数据选取合适的损失分布，从而更加客观地反映真实的给付情况，为监管机构与公司的风险管理者提供参考依据。

二、变点问题研究框架

基于已有研究，本文从变点识别、检验、建模三个步骤建立研究框架体系。在变点识别中，从经典统计学和贝叶斯统计学两个视角识别突变点并衡量其稳健性，进而对初步监测的变点进行检验，分析变点前后的差异，通过信息准则及核密度图等参考依据构建选择模型，具体框架如表1所示。

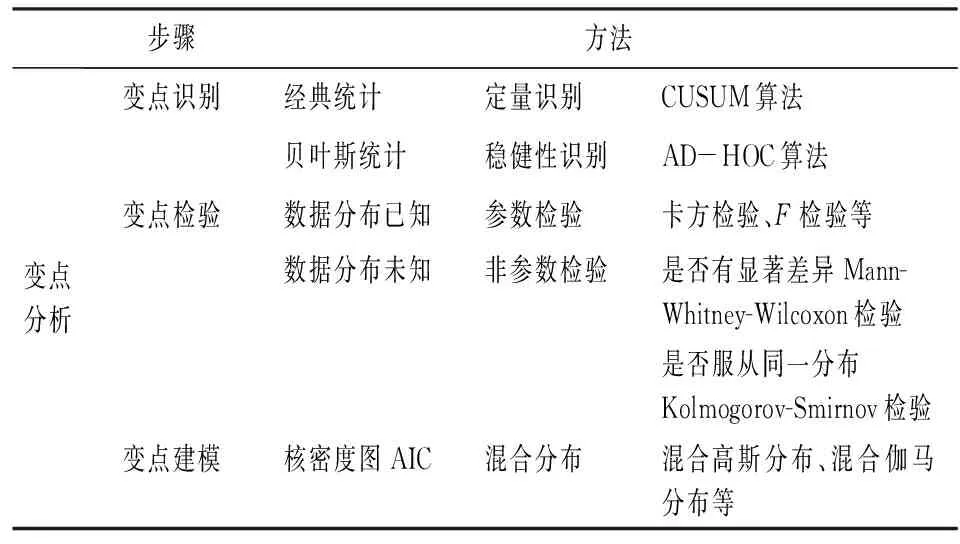
表1 变点问题研究框架

(一)变点识别

比较系统中基本统计量的变化是简而有效的变点识别方法，若系统内存在突变点，则突变后的统计特征量应与之前存在显著差异。本文应用Page提出的CUSUM算法对变点进行识别，这也是近几十年来识别变点的经典算法[18]。CUSUM算法主要通过研究序列均值和方差的信息判断过程是否发生了变化，其基本思想是：给定平均水平条件θ，将每个监测量与平均水平差的累加和(Cumulative Sum)作为观察对象，当监测量的CUSUM明显比正常平稳运行条件下的平均水平高或者低时，意味着系统内发生了变化。一般通过监测样本的均值、方差等统计量作为平均水平条件，这里采用均值进行系统变点识别，具体的CUSUM算法为：已知观测序列x1，x2，…，xn，给定监测均值θ，累计加总值Sr为：

(1)

逐个计算从0到n期Sr的值，定义m为检验统计量：

(2)

m为当期Sr与此时段内最小Sr值之差，h为阈值，给定h后，在r时刻m≥h即检验统计量超过阈值时，r所对应时刻的点即为变点。

基于CUSUM算法找寻突变点，很大程度取决于监测均值θ及阈值h的选取，且对于所确定变点没有进行概率测度以检验选取值的可信程度，针对上述情况，统计学者引入贝叶斯统计方法来解决变点估计不稳健的问题，将所研究的变点问题视为随机变量而非单一点来推断变点在各个时刻的发生概率。关于贝叶斯变点问题已有许多学者展开相应研究，讨论不同数据结构特征下识别突变点的解决方法。Chernoff和Zacks提出的贝叶斯单一变点(At Most One Change，AMOC)识别法[19]。算法基于数据服从正态假设的特征，预先给出每一时刻发生突变的先验概率，根据序列的均值和方差关系，利用贝叶斯模型推断出每一期变点发生的后验概率。该方法考虑了序列每一时期发生变化的特征且估计具有稳健性，对单一变点的识别具有非常良好的效果。

Chernoff和Zacks对服从正态分布单一变点序列的均值进行了贝叶斯估计，指出若序列前期存在有较大变化的非突变点，其可能掩盖后期存在的真实变点使估计非有效。由此二人提出了点对点(AD-HOC)过程改进估计量的不足，该算法不仅能识别单一变点，对多变点也能进行有效识别且同样具有稳健性。AD-HOC过程从最后一期数据出发，倒序观测到第一期对每个点进行后验概率估计，避免了早期过高的非突变点造成的误判问题。设n期序列x1，x2，…，xn，每期发生突变的先验概率为p，初始p0=0，由最后的第n期开始观测，观测序列数据个数由2到m(2≤m≤n)期逐期递增，则从最后一期数据出发的后m期个观测样本在第k(0≤k≤m-1)时刻发生突变的后验概率为B(m，k)为：

(3)

k=0，1，…，m-1

X(m)=(Xn-m+1，…，Xn)

(4)

(5)

(6)

式(3)给出了每一时期发生突变的后验概率，其中式(4)为从最后一期到n-m+1时的序列，式(5)为通过先验概率计算得到的在第k期发生突变的概率，式(6)中的ψk(X(m))为贝叶斯后验估计算子，其中：

(7)

(8)

(9)

式(8)与式(9)为m期观测样本在k时刻突变前后序列的均值，σ2为序列整体的方差，通过式(4)～式(9)可计算得到式(3)的后验突变概率B(m，k)。

(二)变点检验及建模

变点的识别需通过统计检验验证其合理性和科学性。当数据分布已知时，可由参数检验方法来进行变点的检验，现实中的数据往往其分布是未知的，因此经常采用经典的非参数统计检验方法对变点前后样本进行检验。分为两部分进行：一是检验变点时刻前后是否有显著差异，二是检验其统计分布是否相同。关于分析变点的差异性，非参数检验的思想是，若变点在经济系统内呈现相同的周期性规律，则其数值大小顺序即秩统计量应该相同。此外进行建模时还需对数据的分布进行验证，检验变点前后是否服从于同一分布。通常选用Mann-Whitney-Wilcoxon检验数据的结构差异[20]，选用Kolmogorov-Smirnov检验数据的分布差异[21]。

存在变点的数据分布通常呈多峰特征，其分布具有明显差异，混合分布模型是建模的首选，其基本形式为：

f(x)=p1f1(x)+p2f2(x)+…+pnfn(x)

(10)

f(x)为概率密度函数，n为分布峰的个数，通常为变点个数值，p为权重，p1+p2+…+pn=1，关于概率密度函数的选取，通常以信息准则为依据，利用赤池信息量准则AIC对模型进行选择：

AIC=2k-2ln(L)

(11)

k为参数个数，n为样本量，ln(L)为似然函数对数值，选取较小AIC值的模型确定分布。当样本量较小时，Hurvich和Tsai将式(11)进行修正[22]，给出了小样本情形下的信息准则值AICc：

(12)

三、实证分析

(一)数据选取、处理与描述性统计

自改革开放以来，我国财产保险业发展迅猛，“十一五”发展期间，整体实力与经营效益显著提升，保费规模不断扩大，2016年财险业务原保费收入达8 724.5亿元，同比增长9.1%，赔付支出4 726.18亿元，增长12.7%，与保费收入增长趋同，然而在赔款支出方面却高于保费增长，保费收入与赔付支出的不匹配为财险公司带来隐忧，这需要实时把握保险公司的运营情况，对损失赔付进行动态监测以便及时分散经营过程中的理赔风险。保监会发布的经营情况表基于《关于印发〈保险合同相关会计处理规定〉的通知》(财会[2009]15号)的有关内容，根据《企业会计准则(2006)》设置的统计指标，确认本期(年初到当月的累计数据)保险企业的原保险合同保费收入及支付的原保险合同赔付款项。按照该准则及《保险合同相关会计处理规定》的相关规定，保险公司在确定保费收入与赔款支出时应考虑通货膨胀因素，在确定通货膨胀率假设时与采用的折现率假设保持一致。按该口径，各保险公司基于一定的通胀费用假设对原保险赔付支出数据加以报送[注]在通货膨胀时期，保险公司的费用率会因为工资等成本的上升而提高，不及时进行调整和控制通货膨胀带来的影响将使公司的利润下降。因此在保险产品定价过程中，精算师应建立通货膨胀与损失率、利率、费用率之间的量化关系，间接的将通胀因素作为定价要素，提高定价及赔付支出对通货膨胀的适应性。。

使用本年累计数据有利于对经营状况的整体把握，但无法反映月度之间的变化情况和规律，不能识别个别月度赔付存在的支出较大的异常风险点和揭示赔款支付之间的异质性特征，使得潜在的经营风险被忽略。一年中个别月度的重大赔付导致月度保费收入与赔付支出的资产负债不匹配，这不利于保险公司的健康运行，因此要将经营数据按月划分进行更细致的分析。根据月度赔付情况的监测结果识别重大赔付风险点对分散控制理赔风险具有重要作用，可以更客观地认识财险公司一年期的经营状况，为监管者提供更有针对性的经验证据，以加强对重点月份的监督管理，给公司内部控制和风险管理提供更详尽的参考依据，对商业车险的市场化改革、科学厘定费率和财险责任准备金的评估也具有一定的指导作用。

本文采用保监会2010—2016年度每月发布的保险业经营情况表中财产险原保险赔付支出数据，每月的原数据是本年累计存量数据，为更客观反映每月的赔付情况和便于突变点的识别，本文整理加工拆分为逐月度的流量数据，整理后月度的时间序列如图1所示。

图1 2010—2016年我国财险赔付支出金额图(亿元)

随着我国财险业务规模的扩大，赔付支出近7年来也在有条不紊的增加，年累计值也由2010年的1 756.03亿元提高到2016年4 726.18亿元，增长达270%，月度赔付也由100多亿增至400余亿元，个别月份已高达500余亿元。从图1直观来看，财险赔付呈有规律的周期波动增长，每年一至三季度平稳变化，四季度初呈显著突变急剧增长，大体有“年初降”“年末涨”的给付现象：在每年度2月份给付金额下降，10月后明显有大幅上升，出现“翘尾巴”的折点，其余各月变化较为稳定。对于财险公司需对赔付金额增加的关键风险点加以重视。图1的变化规律引发了对赔付支出变化的关注，即11月是否为赔付突变增长点，1～10月的赔款支出是否与11～12月存在显著差异，其变化的趋势是偶然还是阶段的周期性规律，假设突变点存在，构建何种损失模型更能恰当地拟合赔付数据。首先需要对假设的变点进行初步的识别，根据图1中的数据初步看出近7年来赔付的月度序列呈现相同的变化规律，仅从赔付金额上看，逐年上升平稳上移。因篇幅所限，以最近2016年月度数据为例进行分析说明。

2016年度我国财险公司原保险赔款给付金额共计4 726.18亿元，创历史最高水平，将当期数据按月度进行拆分，2016年12个月我国财险赔款给付描述性统计如表2所示。

表2 2016年度财险月度赔付支出描述性统计表 单位：亿元

由表2看出，2016年1～10月与11～12月我国财险赔款给付均值与标准差存在明显不同，1～10月损失均值与11～12月均值相差161.02亿元，方差波动较大，全年极差相差达309.38亿元，初步推断11月前后赔付具有差别。

(二)赔付支出的变点识别

运用CUSUM算法对赔付支出进行定量识别，该算法的一个重要问题是监测均值θ的选取，θ必须恰当反映观测对象平均水平，过低或过高都会使得算法估计失效，为了保证算法估计的准确性，选取2016年全年、1～10月(排除四季度上升的时间段)、4～10月(排除一季度下降与四季度上升的时间段)的三组平均值作为监测均值，分析其变化的敏感性，其数值分别为393.85、367.01、370.60亿元，由3组均值可以看出，全年平均水平较之后两组有显著不同，一季度下降对整体影响不大，四季度变化对整体有很大影响。以h=80作为阈值，计算后得到3组m值的序列，用折线图直观表示如图2所示。

图2 不同监测均值下CUSUM检验统计量序列图

由图2可以看出，不同均值监测下的检验统计量值均在11月份呈现明显的突变趋势，斜率骤然增加。1～10月份变化大体一致，在三季度后m值出现分层，以1～10月、4～10月均值度量下的m值在11月超过阈值h，两者监测均值仅相差3.584，但在7月后m值却产生显著不同。以全年均值度量的m折线图变化趋势在1～10月较为平缓，m值较小有8个月为0，11月并未超过h，但与前三季度相比差异明显，平缓原因是由于监测均值选取过大致使Sr过小影响了m的计算，但不影响从序列图中判别其变化趋势。从3组检验统计量序列折线图的比较来看，剔除一、四季度赔付波动较大变化月度的监测均值来计算检验统计量较为适宜，能很好反映年度的平均水平，更有利于变点的识别。此外，不同h值的选取也会影响结果的判断，当h过小时很可能造成对变点的误判，在图2中若h小于80，按CUSUM判别方法在1～10月、4～10月可能出现多个突变点，仅从数字而不从图形来推断，很可能造成对变点的错误推断，这需要对变点算法进行改进使之更加稳健。

利用贝叶斯AD-HOC算法检测变点识别的稳健性，为简化计算过程，不致使得式(7)方差过大，对赔付数据进行标准化处理，将其方差调整为1，假设每期发生突变的先验概率p为0.5，后验概率B(m，k)如表3所示。

表3表示了从12月出发，选取m个赔付数据在12-k月发生突变的后验概率，每一行加总后的后验概率之和为1。B(m，0)表示没有突变发生，B(4，3)表示选取后四月赔付数据作为观测对象，在第9月中发生突变的概率为0.14。由此得到了一年12个月所有赔付数据的B(m，k)。由表3看出，k=1、2时刻即10～11月之间选取任意m个观测样本的突变概率显著高于其他月份，在20%～52%之间，其中最小值20%已远远大于其它时刻的最大值，由此可以推断序列突变时刻在此之间。为了检测先验概率p的选择对后验概率结果的影响，对过程进行敏感性分析，考虑系统内突变发生较小的概率假设，设先验概率p=0.05，其后验概率B(m，k)如表4所示。

表3 突变点后验概率表(p=0.5)

表4 突变点后验概率表(p=0.05)

由表4可以看出，除k=0突变未发生外，p=0.05时k=1、2，突变点后验概率表(p=0.05)时刻后验概率较之其他时间依然最高，在5%～16%之间，与p=0.5得到的变化结果一致，通过表3与表4的对比可以看出B(m，k)对p取值不敏感，AD-HOC算法识别的变点结果与先验概率的选取无关，结合贝叶斯模型使得估计量具有很强的稳健性，对于序列后期的单一突变以及多变点情况下的识别问题有着非常好的估计效果，较之CUSUM算法更加有效，是后者的改进和进一步补充。通过数据的描述性统计，结合两种算法的结果，进一步推断11月份为赔款给付的突变点。

(三)赔付支出变点的非参数检验

识别变点后，分别对2010—2016年7年的数据进行统计检验，每年中1—10月份赔付数据分为一组，11—12月两个数据分为一组，选用Wilcoxon-Mann-Whitney非成对样本组的秩次和检验来检验两组间是否有显著差异，检验非成对样本容量为n1的观察值X1，X2，…，Xn1和样本容量为n2观察值Y1，Y2，…，Yn2的中位数是否相等，若相等则无差异，设原假设H0∶M1～10=M11～12(10月前后赔付无差异)，备择假设H1∶M1～10

假设X1，X2，…，Xn1来自分布为F(x)总体的样本，Y1，Y2，…，Yn2来自分布为G(x)总体的样本，F(x)、G(x)均未知且均为连续分布函数，检验两者分布是否相同，即原假设为H0：F(x1，x2，…，x10)=G(x11，x12)，备择假设为H1：F(x1，x2，…，x10)≠G(x11，x12)，采用Kolmogorov-Smirnov(K-S)双样本检验来观察两组观测值，K-S检验基于累计分布函数，用以检验一个经验分布是否符合某种理论分布，或比较两个经验分布是否有显著差异。相比于其它检验，K-S检验适用范围不仅能用于正态分布，还能应用于分布有偏的损失赔付数据，用R软件中的ks.test函数对各年的两组数据进行K-S检验，p值均为0.030 3，对7年整体的两组数据检验p值为0.005 57，在5%的显著性水平下接受备择假设，即10月前后赔付数据的损失分布不同。通过W-M-W与K-S检验，确定识别的每年11月份为赔款给付突变点，各年度月度损失大小不同，但趋势及变化规律相同，损失分布在变点前后发生改变。

(四)赔付支出的变点模型

检验确定变点后，需选择合适的损失模型拟合赔付数据，给出其统计分布。变点前后数据的差异决定了需要通过不同的模型加以研究，由于保险公司风险特点，赔付的损失分布往往不同于传统大样本情况下服从大数定律和中心极限定理的正态分布“钟型”曲线，而是呈现“尖峰厚尾”特征，故选取正态分布、指数分布、对数正态分布、伽马分布及帕累托分布等典型损失模型，对2010—2016年7年的变点前后的赔付数据分别进行拟合，利用极大似然法(MLE)估计模型中的参数，R软件nloptr程序包中的nloptr函数可进行非线性模型参数的极大似然估计求解，由变点检验可知1—10月与11—12月服从不同分布，假设1—10月服从分布F(x，θ)，11—12月服从另一分布G(x'，λ)，则整体的极大似然函数为：

L(θ，λ)=L(xi1，xi2…xi12，θ，λ)

(13)

五种损失模型的结果如表5所示。

表5 赔款给付分布及参数的极大似然估计

表5给出了变点前后两个局部与整体三者模型参数的似然估计。1～12月份表示了假设无变点情况下，赔款给付服从同一损失分布F(x)=G(x')的值，利用赤池信息量准则AIC对模型进行选择，本文中损失样本数据仅为84个，因此选用小样本情形下的信息准则值AICc选择损失分布。

除指数分布外，本文拟合的损失分布模型参数个数均为2，样本量也相同，因此影响AICc大小的决定因素为模型的似然函数值L，它反映了数据信息量的使用程度，AICc的数值结果如表6所示。

表6 5种损失模型的AICc

由表6中的AICc值可以看出，除帕累托分布外，变点假设下1～10月、11～12月分段拟合的同一模型不同参数下损失分布的AICc之和(3)小于无变点假设(4)下模型的AICc，分段模型优于整体服从单一参数的模型，再次证明了突变点的存在性及变点前后采用不同损失分布“分而治之”拟合赔付数据的合理性。根据最小信息原则，AICc最小值组合min(1)+min(2)即为最佳的损失模型。在1～10月，应选择AICc数值最小的正态分布模型；而在11～12月中，正态分布、对数正态分布、伽马分布的AICc数值近似，因此三类损失分布均可作为变点时期的数据建模。考虑模型构建的连续性与简约性，最终选择变点前后均为正态分布的损失模型。

图3给出了用R软件绘出的给付分布核密度概率图，从7年赔付数据整体来看，可见赔款给付分布呈双峰特征，使用单个连续模型拟合的结果往往不尽人意，在这里混合分布(Mixed Distribution)有效地解决了数据多峰问题，在常用的模型之间可以起到“取长补短”的作用[23]。

图3 整体赔款给付直方图及核密度曲线图

根据表6中AICc(3)的结果，选择前后均为正态分布的混合模型，图3核密度曲线呈双峰特性，选取n=2，构建的混合模型即为二元混合高斯模型：

p1+p2=1

(14)

在混合模型的各种参数估计法中，常用矩方法和极大似然估计法，极大似然估计法在计算上复杂但在参数估计中具有一致性和有效性，这里采用混合高斯分布中极大似然估计的EM算法来确定模型中的待估参数，R软件中mixdist程序包专门用来进行混合模型的拟合和参数估计，对数据按区间进行划分，使用mix函数，运用EM算法计算参数的估计值为p1=0.147，p2=0.853，μ1=152.13，μ2=293.56，σ1=37.523，σ2=88.316。p1、p2的估计值较为接近变点前后期间的月度权重2/12与10/12，估计出混合模型的概率密度分布与核密度曲线对比及概率分布函数如图4、图5所示，混合模型的拟合效果非常良好，较好地解释了赔款给付的差异性特征，揭示了整体赔付数据的分布规律及变点前后损失分布的异质性。

图4 混合高斯模型概率密度图

图5 混合高斯模型概率分布图

一年之中10月后财险公司赔款给付额的增加，从投保人来看，年末是交通事故的高发期，冬季车辆安全性能降低，私家车使用频率在岁末显著上升，除了对道路造成拥挤外，事故发生的概率也会提高，导致了赔案的集中赔付。从保险公司角度来看，年末赔付的增加一方面带来了经营压力，不利于企业的正常运行，同时从内部角度分析，赔付的增加可能是财险公司人为调控的结果，通过对赔案赔款给付时间的操作可以控制一年内的经营情况，使得一年中的大部分月度呈现出良好的运营状态，较低的经营赔付率有利于改善渠道部门的考核指标。公司决策者应制定合理的内控制度来优化赔付系统，确保及时对保险人的赔案进行处理。从外部角度分析，将已报案已决赔款集中到年末给付可以增加保险公司支出的费用和营业成本，降低利润，起到合理避税的作用。监管机构对此类现象应进行严格监控，确保财险市场良好的竞争环境。财险公司管理者在年末应制定合理措施分散风险，加强核赔程序，客观真实地反映经营状况，精算人员应适当增加未决赔款准备金份额以确保集中赔付，对赔付率进行更合理科学化的计算。

四、结论

本文构建了一种变点统计的研究框架，运用经典统计学的研究方法，从变点识别、检验、估计三方面展开讨论，通过对近7年来我国财险赔付月度数据的拟合，得到如下发现：一年中的11月为赔款给付的突变点；突变前后服从不同参数的正态分布，整体赔款给付为双峰特征的混合高斯分布；由于结构性突变点的存在，数据分布通常呈现多峰特征，由单分布变为混合分布，通过信息准则可以对混合分布模型进行选择，所有数值结论都可以使用R软件相应的程序包计算得到。本文所用变点分析方法也可应用于其它问题，由单一变点拓展到多变点，由低维数据延伸到高维数据，检验其它关键性的金融风险指标，在数据分布的选择上，可以根据数据自身结构推广到更一般的模型。