基于因子分析和改进DEA交叉模型的中国“一流大学”建设高校科研效率评价

，鲁玉

(郑州大学 商学院，河南 郑州 450001)

一、引言

高校科研是中国科研工作的重要组成部分，是培养创新型人才的重要机构。近年来，高校科研呈现出科研项目数量多、类型多和科研经费资助金额高等特点，产生了一批具有国内外领先水平的科研成果。面对前所未有的科技资源投入，高校科研投入产出效率已成为社会各界关注的焦点，而如何通过科学地评价与合理地监控提高科研效率，亦成为高校科研管理领域研究的热点。

高校科研效率评价的目的不在于结果，更在于它指明了改进方向。2017年9月21日，教育部正式对外公布了世界一流大学和一流学科(简称“双一流”)建设高校及建设学科名单。此次名单涉及一流大学建设高校42所，一流学科建设高校95所。“一流大学”建设高校在培养人才、提高创新水平、传承优秀文化等方面是未来中国高等教育的主力军，更是高校“内涵发展、特色发展”的导向。因此，本文通过利用改进DEA交叉模型对“一流大学”建设高校科研效率的评价，摸清其科研资源、力量、成果的分布情况，找出各高校比较优势和问题，不仅对促进高校科研资源科学配置具有重要意义，而且能够引导高校自我诊断和完善，为“双一流”建设明确目标与方向。

二、文献回顾

早期高校科研效率评价主要涉及高校科研产出和科研竞争力的测度，如De Groot等采用研究成果评价数据和结合同行评议的方法，对美国高校科研产出进行了评价[1]；Abbas Valadkhani等运用聚类和因子分析对澳大利亚部分大学的研究绩效进行了分类评价[2]。为了进一步探究科研投入与科研能力的关系，20世纪90年代，G.Johnes和J.Johnes较早地运用DEA方法对英国大学经济系科研效率进行评价，并通过对比同行评议结果指出DEA在科研绩效评价上有积极作用[3]。国内方面，香港学者Ng 和Li 最早在2000年运用DEA方法对内地高校科研效率进行评价，随后国内外学者不断拓展DEA方法并从不同维度对科研效率进行测评，DEA方法已成为科研效率评价中被广泛采用的工具[4]。

梳理文献发现，现有应用DEA方法对科研效率进行评价的研究可分四类：第一类是应用DEA基本模型，即CCR模型和BCC模型进行分析。张大伟等利用DEA的CCR模型评价了某高校13个工科院系的科研效率[5]；李瑞等利用BCC模型对29个地区高校2009—2014年的投入产出效率进行评价[6]。第二类是应用DEA模型与Malmquist生产率指数等方法相结合，从静态和动态角度评价高校科研效率。苏为华等利用BCC模型评价浙江省高校的静态效率，进而结合Malmquist生产率指数评价浙江省高校的动态效率，结果显示浙江省科研效率有效的高校所占比例仅为20%左右[7]；闫平等利用DEA与Malmquist生产率指数从静态和动态角度评价了教育部直属48所高校的科研效率，结果显示大部分科研效率没有达到有效水平[8]。第三类是运用超效率DEA模型，弥补CCR模型和BCC模型只能将决策单元区分为有效或者无效并不能实现决策单元全排序的不足；倪渊提出了滞后非径向超效率DEA模型，应用该模型评价了36所高校的科研效率，通过与标准DEA进行对比分析验证了该模型的有效性[9]。第四类是为解决传统CCR模型、BCC模型、SE-DEA模型得出的效率值都是自评效率值，且评价出的决策单元可能存在“伪有效”的问题。Sexton等提出的DEA交叉模型不仅考虑了自评效率值还考虑了互评效率值，使评价结果更客观[10]，但由于其最优权重不唯一，模型得出的交叉效率可能不唯一；进而，Doyle等提出仁慈型交叉模型和对抗型交叉模型[11]，但两种改进模型得出各决策单元的效率值和排名不一致，并且没有给出模型偏好选择的标准；基于此，Wang等提出了中立型DEA交叉模型[12]，但其分式规划模型和线性规划模型不等价，无法得出唯一的权重和效率值，同时在集结各高校科研效率值时多采用每列的平均值得出每个决策单元的综合交叉效率值，而没有充分考虑各个决策单元交叉效率值之间的离散程度。

因此，本文评价方法首先将TOPSIS思想引入DEA交叉模型中，建立基于理想决策单元的DEA交叉模型，不仅可以更好规避对仁慈型交叉模型和对抗型交叉模型的偏好选择难题，而且能够解决中立型交叉模型中分式规划和等式规划不等价造成的效率值不唯一的问题，并且遵循了DEA考虑有利于被评价决策单元自身效率的基本思想；在得出交叉效率矩阵后，采用熵权法对各高校效率值进行集结，以反映各高校交叉效率值之间的关联性，得出客观的效率值，使评价结果更符合实际；为满足DEA模型对指标技术的要求，采用因子分析消除指标关联性并构建评价指标体系；应用改进的DEA交叉模型评价分析“一流大学”建设高校科研效率，并提出改进建议。

三、改进DEA交叉模型

DEA方法及其模型自1978年由美国著名运筹学家A.Charnes和W.W.Cooper提出以来[13]，已广泛应用于不同行业及部门，并且在处理多指标投入和多指标产出方面体现出其得天独厚的优势。TOPSIS法是根据有限个决策单元与理想决策单元的接近程度进行排序，若其中的一个决策单元比另一个决策单元在距离上更接近理想决策单元，则该决策单元在排序上更优于另一决策单元；引入理想单元之后原本有效的决策单元转化为无效的决策单元，进而实现决策单元的全排序。本文将TOPSIS 思想引入到DEA交叉模型中，在保证决策单元自评效率值不变的前提下，选择出一组使理想决策单元交叉效率值最小的最优权重；然后利用该权重评价其他决策单元，得到交叉效率矩阵E，使其他决策单元交叉效率值与理想决策单元交叉效率值差距较小，从而坚持了最有利于被评价决策单元的原则。

首先，构建理想决策单元。设有n个部门或单位构成决策单元DMUj(j=1，2，…，n)，各决策单元DMUj有m个投入指标xij(i=1，2，…，m)和s个产出指标yrj(r=1，2，…，s)；定义理想决策单元DMUj为用最小的投入获得最大的产出，即：

j=1，2，…，n

其次，求取使理想决策单元交叉效率值最小的最优权重。在决策单元自评的基础上，根据上述设定，可得基于理想决策单元的DEA交叉评价模型为:

(1)

(2)

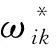
(3)

从而得到交叉效率矩阵E，矩阵中的元素Ekj是决策单元DMUj，j=1，2，…，n，j≠k；利用决策单元DMUk，k=1，2，…，n的权重所获得的互评效率值，对角线上的元素Ekk表示决策单元DMUk的自评效率值。

最后，利用基于理想决策单元的DEA交叉模型得出交叉效率矩阵E之后，需要集结各决策单元的效率值，而现有研究多采用每列平均值进行集结，没有考虑各高校交叉效率值之间的关联性。交叉效率矩阵E中，主对角线上的元素表示各高校的自评效率值；其余元素中，第k行表示的是DMUj对其他高校的评价值，其值越大，表示DMUj的科研效率值越小；第j列表示的是其他高校对DMUj的评价值，其值越大，表示DMUj的科研效率值越大。因此，本文将熵权法引入基本理想决策单元的DEA交叉模型中，构建改进的DEA交叉模型。该模型不仅可以得出客观的效率值，而且可以考虑各高校之间的关联性对交叉效率值进行集结，使评价结果更客观。

四、评价指标、数据与方法

(一)评价指标体系

评价指标体系是高校科研效率评价的基础，本文遵循系统全面性、简明科学性、灵活可操作性、目的明确性等原则[14]，在借鉴现有研究成果基础上构建高校科研效率评价指标体系。本文检索了2008—2018年间关键词为科研效率评价的120篇文章进行统计分析，统计结果见表1。

表1 近10年科研效率评价指标统计表

基于上述统计分析结果，本文将部分指标细化，其中投入指标中研究与发展人员包括科学家与工程师和全时当量人员，科研经费当年拨入是指政府资金当年拨入和企事业单位委托资金当年拨入[15]；产出指标中成果授奖项主要是国家级奖项，学术论文主要考虑的是在国外和全国性刊物上发表的论文，避免只考虑数量不考虑论文质量的缺点；最终建立“一流大学”建设高校科研效率评价指标体系，其中投入指标主要从人、财、科技服务三个方面度量[16]，主要包括教学与科研人员(I1)、科学家和工程师(I2)、全时当量人员(I3)、政府资金当年拨入(I4)、企事业单位委托资金(I5)、科研经费当年内部支出(I6)、科技项目服务数(I7)、科技服务当年投入人数(I8)、科技服务当年投入经费(I9)；产出指标包括专著数量(O1)、学术论文(O2)、成果授奖项(O3)、国家级项目验收(O4)、专利授权数(O5)、科技课题总数(O6)、技术转让当年实际收入(O7)、专利出售当年实际收入(O8)。

本文拟采用DEA模型评价高校科研效率，DEA一个重要应用前提是评价指标间不存在较强的线性关系。为满足DEA模型对指标的技术要求，采用因子分析对指标进行降维处理，消除投入指标间以及产出指标间的线性关系，以提高评价结果的有效性。

首先应用SPSS 20.0对投入指标(I1～I9)和产出指标(O1～O8)进行因子分析，再采用主成分分析法(PCA)构造因子变量。

对投入指标进行KMO检验和巴特莱特球体检验。KMO统计量为0.767(大于0.5)，巴特莱特球体检验的卡方统计量的显著性水平为0.000(<0.001)，因此9项投入指标之间具有共同因素，适合对投入指标进行因子分析；进而提出公因子，根据原变量的方差情况以特征值为原则选取2个公因子，累计方差贡献率为80.308%。

表2是由9个投入指标和2个公因子采用方差极大法旋转后的因子负载矩阵。由因子负载矩阵可知，公因子Fct1对指标I1～I6的影响较大，定义为创新基础能力；公因子Fct2对指标I7～I9的影响较大，定义为环境支持能力。

表2 旋转后的投入指标因子载荷矩阵表

对产出指标进行KMO检验和巴特莱特球体检验。KMO统计量为0.747(大于0.5)，巴特莱特球体检验的卡方统计量的显著性水平为0.000(<0.001)，因此8项产出指标之间具有共同因素，适合对产出指标进行因子分析；接着提取公因子，根据原变量的方差情况以特征值为原则选取2个公因子，累计方差贡献率为77.375%。

表3是由8个产出指标和2个公因子采用方差极大法旋转后的因子负载矩阵。由因子负载矩阵可知，公因子Fct3对指标O7～O8的影响较大，定义为成果转化能力；公因子Fct4对指标O1～O6的影响较大，定义为创新产出能力。

表3 旋转后的产出指标因子载荷矩阵表

(二)研究对象与数据

本文选取42所“一流大学”建设高校为研究对象，由于国防科技大学的保密性要求而无法获得数据，中央民族大学的数据和其他高校具有较大的差异不具有可比性，因此拟对剩余的40所“一流大学”建设高校科研效率进行评价。鉴于投入产出间存在滞后性，设定产出滞后期为2年，投入指标数据来源于《2014年高等学校科技统计资料汇编》，产出指标数据来源于《2016年高等学校科技统计资料汇编》。

(三)评价分析方法

基于DEA的高校科研效率评价中，无论是CCR模型、BCC模型，还是DEA与Malmquist生产率指数相结合的模型以及SE-DEA模型，其评价结果均是自评效率值。自评效率值最大的特点是决策单元会从众多解中选择有利于自身效率最大化的解，导致决策单元对自身有优势的指标设置较大的权重，而对自身不利的指标设置较小的权重，甚至权重为零。DEA交叉模型不仅考虑自评效率值，还考虑互评效率值，综合得出交叉效率值。交叉效率值是指各高校在计算自身科研效率值不仅考虑利用自身权重得出的自评科研效率值，还要考虑利用其他高校的权重得出的他评效率值，进而得到综合平衡交叉效率值，使得评价结果更客观。因此，本文先利用DEA-CCR模型计算 “一流大学”建设高校科研自评效率值，进而通过改进的DEA交叉模型得出“一流大学”建设高校科研综合交叉效率值，具体评价分析方法如下：

1.利用DEA-CCR对偶规划模型计算出各个高校科研自评价效率值：

λj≥0；j=1，2，…，n

i=1，2，…，m；r=1，2，…，s

2.通过理想决策单元DEA模型计算各高校科研交叉效率值，进而以Ekj(k，j=1，2，…，40)为元素构造交叉效率矩阵E：

3.将交叉效率值作标准化处理：

4.通过信息熵衡量各交叉效率值的重要程度，则第j个高校的信息熵为：

5.为拟合交叉效率值，利用熵权法估算各个DMU的交叉效率值所占的权重：

6.综合交叉效率评价值为：

五、实证分析

将40所“一流大学”建设高校科研投入产出指标数据代入CCR模型、仁慈型模型、对抗型模型和改进的DEA交叉模型中。首先运用DEAP软件对40所高校科研效率进行自评，然后利用Matlab计算出40所高校科研效率的综合交叉效率值以及各高校科研效率排名，同时分析利用熵权法得出的权重与简单采用平均权重的区别，进而利用得出的结果进行对比分析，具体结果见表4所示。

表4 “一流大学”建设高校科研效率评价结果表

1.改进DEA交叉模型评价结果分析。由表4可知，改进DEA交叉模型评价结果显示各高校的科研效率水平参差不齐，差距明显，即使排名第一的高校，如中国农业大学科研效率值为0.545 5，仍存在45.45%的改进空间；对于科研效率最小的高校，如中国人民大学科研效率值为0.045 9，存在95.41%的改进空间；每所高校的科研效率都存在不同程度的改进空间，没有一所高校的科研效率是完全有效的，这种评价结果与现实情况相符；通过改进DEA交叉模型得出的40所“一流大学”建设高校科研综合交叉效率值均小于1，均值为0.301 6，处于较低水平：科研效率超过0.5的仅有中国农业大学、南开大学、重庆大学、山东大学4所，占总数的10%；科研效率在0.4～0.5之间的高校有北京理工大学、天津大学、复旦大学、厦门大学、武汉大学和东北大学6所高校，占总数的15%；科研效率值在0.3～0.4之间的高校有清华大学、哈尔滨工业大学、南京大学、中国科学技术大学、中国海洋大学、中南大学、华南理工大学、四川大学、西安交通大学、兰州大学和郑州大学11所高校，占总数的27.5%；科研效率值在0.3以下的高校有北京大学、中国人民大学、北京航空航天大学等19所高校，占总数的47.5%。整体而言，40所“一流大学”建设高校科研效率处于较低水平，存在较大提升空间。

2.DEA交叉模型与传统CCR模型评价结果的对比分析。相比CCR模型，DEA交叉模型采用自评和互评相结合的方法得出效率值，同时DEA交叉模型更注重全部指标体系的相对比较，即将一所高校的全部指标体系与其他高校进行分析比较，因此交叉效率的结果可以反映出全部指标的相对科研效率状况，更符合客观现实的科研效率情况，主要体现在以下两点：一是CCR模型无法对有效的高校进行排序。由表4中通过CCR模型得到的40所高校科研自评效率值可见，清华大学、中国农业大学、天津大学和山东大学4所高校科研自评效率值等于1，这表明上述高校科研效率有效,CCR模型无法对这4所高校进行进一步排序，而DEA交叉模型可以实现对40所“一流大学”建设高校的全排序；二是CCR模型计算出的自评科研效率值较高。如清华大学，其科研自评效率值为1，达到DEA有效，但通过改进DEA交叉模型得到的科研综合交叉效率仅为0.351 6，远低于自评效率值；类似的还有南开大学、天津大学等高校，这些高校自评科研效率值较高的原因是CCR模型在计算自评效率值时对自身有利的指标赋予了较大权重，而对自身不利的指标赋予了较小权重甚至为0，因此自评效率值较高；而采用DEA交叉模型评价结果不仅包括自评效率值还包括他评效率值，由于用DEA交叉模型可以很好地修正自评效率值的偏差，使结果更符合实际情况。因此，本文将采用DEA交叉模型得到的结果作为进一步分析的依据。

3.仁慈型交叉模型和对抗型交叉模型评价结果的对比分析。由表4可知，仁慈型模型和对抗型模型得出各高校的科研效率值和排序是不一致的。比如北京理工大学，利用仁慈型模型计算出效率值为0.381 5，排名16；而利用对抗型模型计算出的效率值为0.365 3，排名13，两种模型得出的结果不一致。Doyle等虽然提出了用仁慈型交叉模型和对抗型交叉模型来解决DEA交叉模型权重不唯一的问题，但两种改进模型得出各决策单元的效率值和排名不一致，并且没有给出模型偏好选择的标准。由于中立型模型的分式规划和整式规划在计算过程中存在偏差，因此本文没有列出中立型模型的计算结果。通过与仁慈型模型、对抗型模型和中立型模型进行对比，本文提出的改进DEA交叉模型可以避免仁慈型模型和对抗型模型的选择难题，同时还可以避免中立型模型分式规划和等式规划不一致的问题。

六、结论与启示

高校科研效率提升是当前中国高等院校科研创新工作亟待解决的核心问题。本文将TOPSIS思想和熵权法引入DEA交叉模型中，建立改进的DEA交叉模型，既克服了传统DEA模型无法有效区分高校科研效率差异问题，又弥补其存在极端权重的缺陷，同时坚持的最有利于被评价决策单元的思想，在集结交叉效率值时考虑了各高校交叉效率值之间的关联性，为高校科研效率评价提供了新思路；同时，采用DEA模型评价高校科研效率的一个重要前提是在于投入与产出指标间不存在较强线性关系，因此本文采用因子分析对指标进行降维处理，消除了投入产出指标间线性关系，在保持原有信息基础上增加了指标选择的客观性，满足了DEA对指标之间的技术要求；最后，运用改进的DEA交叉模型对中国40所“一流大学”建设高校科研效率进行了评价，并得出以下结论：

第一，通过对比分析DEA交叉模型与传统CCR模型的评价结果，交叉模型可以对40所“一流大学”建设高校实现全排序，弥补了CCR模型无法对清华大学、中国农业大学等这些效率值为1的高校排序的缺陷；同时，由于交叉模型计算各高校科研效率值不仅考虑自评效率值还考虑他评效率值，比CCR模型较客观；此外，通过对比分析仁慈型交叉模型和对抗型交叉模型的评价结果可以看出，本文提出的改进DEA交叉模型不仅能够解决仁慈型模型和对抗型模型的选择难题，而且避免了中立型模型分式规划和等式规划不一致的问题，为高校科研效率评价提供了新思路。

第二，40所“一流大学”建设高校科研效率处于较低水平，每所高校存在不同程度的改进空间。通过评价结果可以看到，40所“一流大学”建设高校平均科研效率仅为0.306 1，没有一所高校的科研效率值完全有效。中国农业大学的科研效率值最高为0.545 5，存在45.45%的改进空间；中国人民大学科研效率值最低为0.045 9，存在95.41%的改进空间；科研效率值在30%以下有19所高效，这表明“一流大学”建设高校科研资源利用率普遍较低，故应加强对投入资源的控制，同时采取一定的措施提高高校的科研质量和成果转化。

第三，一些知名度较高的高校的科研效率值较低。比如北京大学、浙江大学等，这种情况主要是由于这些高校知名度较高，从而更容易获得资助，如北京大学教学与科研人员投入和科研经费当年拨入分别为13 030人和2 493 485千元，浙江大学教学与科研人员和科研经费当年拨入分别为15 026人和3 393 870千元，而40所“一流大学”建设高校的平均教学与科研人员和科研经费当年拨入分别为4 801人和1 404 951千元，知名高校的投入远高于平均水平，造成投入冗余、资源不能合理利用、科研效率值偏低的现象。因此，为避免投入资源的低效率配置，应该尽量平衡各高校的投入，并根据各高校的规模合理分配其投入资源，以提高高校的整体科研效率。