基于实验方法的橡胶圆管的本构模型分析

刘洪波，刘 齐，孙国栋

(1.北华大学 工程训练中心，吉林 吉林 132021；北华大学 机械工程学院，吉林 吉林 132021)

天然橡胶作为气动驱动器弹性气囊[1,2]的主要构件，在变形过程中具有大变形和非线性的特点，用准确的数学模型对其性能进行描述十分困难.由于橡胶是超弹性体，弹性体形变能的大小只取决于变形的初始状态和最终状态，与加载路径无关[3-5].因此，通常用应变能密度函数来描述天然橡胶的本构模型和力学性能[4].近几十年来，国内外学者对应变能函数提出了很多假设.其中Mooney和Rivlin提出的Mooney-Rivlin模型、Yeoh和Ogden模型应用最为广泛[6,7].

本文主要对小变形(变形量小于100%)的天然橡胶[8,9]圆管进行单轴拉伸实验，通过数值分析其应力-应变曲线，总结得到了适合小变形下橡胶的应变能密度函数及其材料系数.

1 橡胶的本构方程

通常，橡胶应变能密度函数是变形张量的不变量I1，I2和I3的函数[10]，即

W=W(I1,I2,I3)

(1)

因为单轴拉伸时，另外两个方向自由，设拉伸方向的伸长率为λ，应变为ε，则得：

(2)

将(2)式代入(1)可得应变恒量可得：

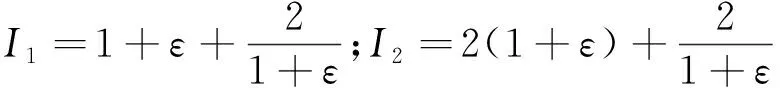
(3)

将(3)代入到应变能密度函数的解析式中并对其应变张量求导可以得到橡胶拉伸时的应力应变关系式:

(4)

式中：NH1、MR1及Y1分别对应表示Neo-Hookea模型、Mooney-Rivlin模型和Yeoh模型；CNH1、C10、C01、C1、C2和C3为各模型中对应的材料系数.

为了便于计算，对(4)式对应用泰勒级数展开，得到三种本构模型的多项式：

σNH1=2CNH1(4ε3-3ε2+3ε)

σMR1=2C10(4ε3-3ε2+3ε)+2C01(10ε3-6ε2+3ε)

σY1=2C1(6ε5-5ε4+4ε3-3ε2+3ε)+12C2(8ε5-4ε4+3ε3)+54C3(3ε5-ε-1)

(5)

式(4)与(5)均反映出的应力与应变之间的关系.

2 橡胶圆管单轴拉伸实验

2.1 单轴拉伸实验

实验橡胶圆管为乳胶管，其硬度为43HRC，尺寸规格8*11，有效长度为50 mm.实验时，乳胶管上下两端通过自制简易夹具固定在拉伸机上(图1)，在室温下以5 mm/min的速度施加轴向载荷，设置拉伸参数[10]，使得乳胶管伸长量达到100%时停止加载(图2是拉伸过程中，载荷随伸长量变化的实时曲线)，如此反复5次，取实验的平均值作为最终的实验数据.

图1 实验装置图

图2 拉伸过程中的数据变化过程

实验时所测应力：

(6)

式中：F为负载；A0为乳胶管的横截面积；D1为乳胶管外径，D2为乳胶管内径.

实验时所测应变：

(7)

式中：Δl为乳胶管被拉伸的位移变化量，L为乳胶管原始长度.

将最终获得的试验数据导入MATLAB中，进行处理，得到曲线(图3).

ε图3 拉伸时应力与应变的变化曲线

2.2 材料系数拟合

利用MATLAB对式(5)中的个模型本构方程进行曲线拟合，可以得到相应的模型拟合曲线(图4).

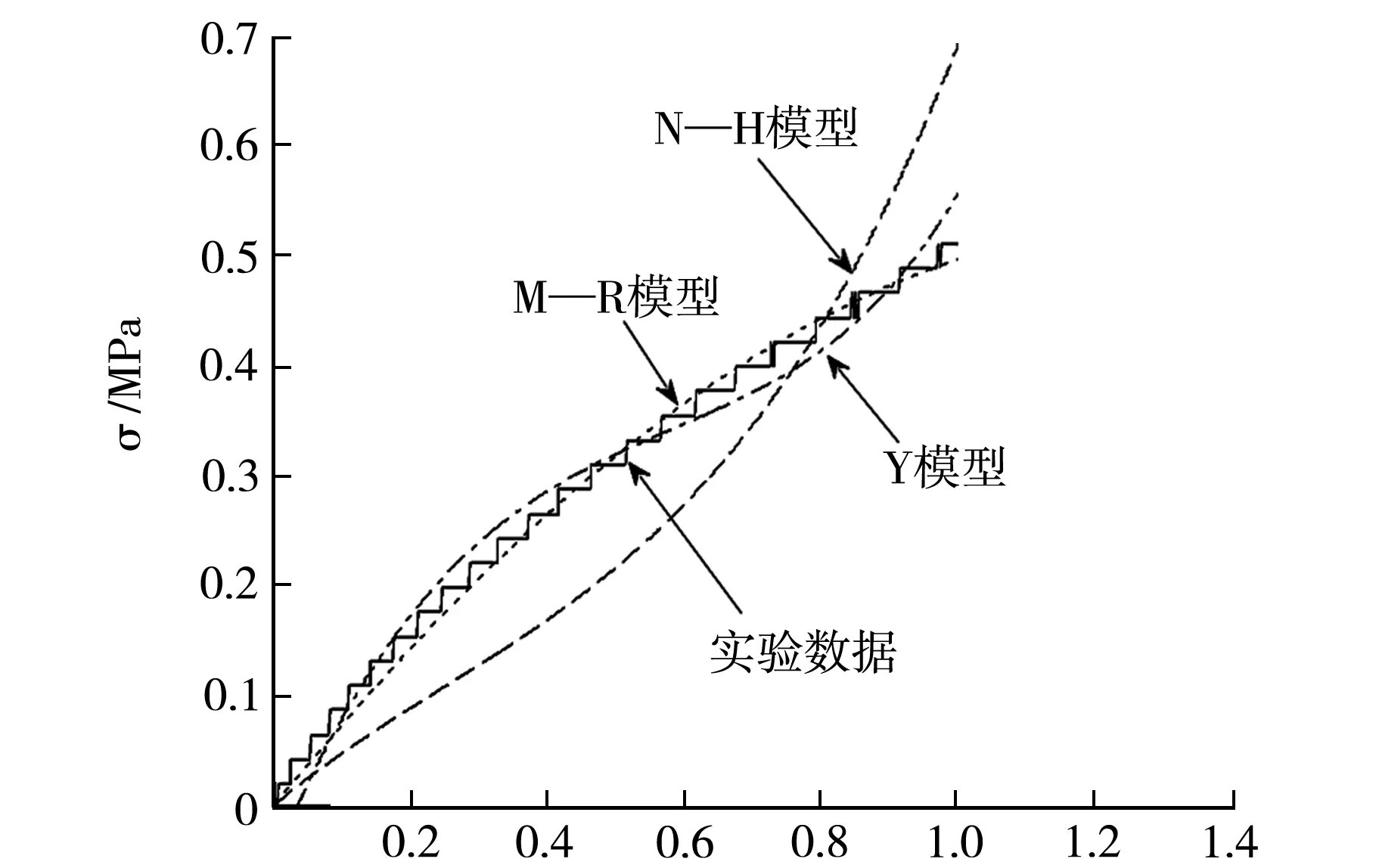
ε图4 拟合曲线图

拟合出各模型的材料系数如下所示：

N-H模型参数CNH1=0.086 7；M-R模型参数C10=0.213 8，C01=-0.086 77；Y模型的参数C1=0.242 5，C2=-0.023 9，C3=-0.000 9.

经对比易知：在小变形(变形量小于100%)时，M-R模型与实验数据拟合效果较好.

3 结 论

本文利用单轴拉伸的实验方法，首先得到了天然橡胶圆管的应力应变曲线，然后通过已有的本构方程与实验数据进行拟合，最终确定了橡胶中常用的三种本构模型的材料系数.通过实验对比，结果表明，M-R模型适用于变形量小于等于100%的范围.实验结论具有一定的借鉴意义，为后续气动人工驱动器变形机理研究提供了实验依据和理论基础.