样点邻域同构曲面约束的散乱点云曲率估计
2018-12-12梁增凯孙殿柱薄志成李延瑞林伟
梁增凯,孙殿柱,薄志成,李延瑞,林伟
(1.山东理工大学机械工程学院,255049,山东淄博;2.西安交通大学机械工程学院,710049,西安)
曲率是曲面信息度量的重要指标,可反映曲面任一点处局部几何性质,在数字化设计与制造、医学辅助设计、文物保护等领域具有广泛的应用价值。三维扫描设备的发展使得获取反映物体细节特征的密集点云数据成为现实,但所得数据通常只包含样点位置坐标且拓扑信息缺失,因此准确估计散乱点云曲率对不同视角的点云配准、特征识别以及曲面重建等后续处理具有重要意义[1]。
现有点云曲率估计方法主要分为基于样点k邻域点集拟合的方法和基于三角网格的方法。Hoppe等采用主元分析法拟合采样点的k邻域点集,通过曲面变分求取其近似曲率[2]。Gumhold等选用移动最小二乘法对样点邻域进行二次曲面拟合,构造逼近原始曲面的局部参数曲面,基于所得参数曲面估计样点曲率[3-4]。Ernest等通过坐标变换构造抛物面,并基于加权拟合有效降低了曲率估计值的误差[5]。然而,基于样点k邻域点集拟合的方法在高复杂度的模型外表面和尖锐特征区域难以寻找合适的拟合曲面形式,限制了曲率估计的适用范围。基于三角网格的方法通常先对散乱点云进行曲面重建,依据重建所得网格结构建立数据间拓扑关系,进而准确估计样点曲率。其中Taubin在三角网格顶点处建立近似矩阵,通过求解矩阵特征值估计顶点曲率[7];Meyer等基于Voronoi元与有限元定义离散的微分几何算子,利用微分几何中的Green公式进行离散化求解,使计算结果准确性进一步提升[8-9]。基于三角网格的方法参考样点局部属性,能对不同区域样点曲率进行准确估计,应用范围更为广泛。
在实际扫描原表面获取点云过程中,因测量距离及扫描角度的变化,即便对于光滑曲面,仍会存在采样误差。特别当点云模型坐标出现法向偏移误差时,曲面G2连续性[10]难以延续,从而导致现有基于重建网格曲面的曲率估计方法计算结果存在偏差且过渡不够平滑。为解决这一问题,本文将目标样点的邻域点集作为局部样本进行曲面重建,获得插值于采样点集且与原表面拓扑同构的局部网格曲面,基于网格曲面中一阶邻域面估计样点曲率,进而依据网格曲面上测地距离对样点曲率估计结果进行修正。在曲率估计的过程中,基于一阶邻域面形心权重计算所需的样点法向,提高曲率估计的精度与稳健性。实验结果表明,该算法具有较高的计算效率,能够有效抑制曲面采样误差的干扰,使得样点曲率估计结果过渡更为平滑。
1 曲面局部拓扑重建
为获得插值于采样点集的高质量Delaunay三角网格曲面,本文依据局部平坦程度,采用二维Delaunay网格剖分与三维Delaunay网格过滤相结合的策略重建局部样本。对于采样点集S中目标样点p,将p的k邻域点集作为局部重建样本,通过适度扩大邻域搜索范围对该样本进行辅助点添加。设kη为获取λ(p)时所需的邻域点集数量,kξ为添加辅助点后邻域点集数量,局部重建算法的具体流程如下。
(1)搜索p的kη邻域,获得局部重建样本λ(p)。
(2)搜索p的kξ邻域点集,获得包含辅助点的局部重建样本φ(p)。在φ(p)中,若∃pi,pi∈φ(p)且pi∉λ(p),则将pi标记为辅助点。
(3)对φ(p)中样点进行共面检测,若共面,则对φ(p)进行二维Delaunay网格剖分,输出剖分的局部重建网格,程序结束。
(4)对φ(p)进行三维Delaunay网格剖分,获得四面体集合D(φ(p)),并求出对应的Voronoi图V(φ(p))。
(5)对D(φ(p))中任一面片Ti进行夹角检测,若检测未通过,则将Ti从D(φ(p))中删除,否则保留。
(6)对D(φ(p))进行流形提取[11],输出局部重建网格,程序结束。
在上述步骤(5)中,对Ti进行夹角检测的具体流程如下:
(1)提取面片Ti的顶点{v1,v2,v3};
(2)检测每个顶点的标记,若三个顶点中存在辅助点,则该面片未通过检测,程序结束;
(3)获取面片Ti对偶Voronoi边的端点b1、b2;
(4)对于顶点v1,计算Voronoi单元中与其距离最远的Voronoi顶点,并将由v1指向该顶点的向量记为Vv1;
(5)计算v1b1和v2b2与Vv1的夹角θ1和θ2,其中θ1=∠(v1b1,Vv1),θ2=∠(v1b2,Vv1)。对于给定阈值θp,若θ1与θ2均小于θp,或θ1与θ2均大于π-θp,则该面片未通过检测。对v2和v3进行相同操作。
局部样本λ(p)的重建效果如图1所示。

图1 曲面局部重建结果
2 基于形心权重的样点法向估计
基于三角网格估计样点曲率时通常需要计算样点法向,且样点法向估计的准确度对计算曲率的准确度有很大影响。由局部曲面重建获得的Delaunay网格曲面包含着样点之间的拓扑关系,可基于网格顶点的邻接信息计算样点法向。对网格曲面,顶点的一阶邻域如图2所示。可将一阶邻域面法向的加权和表示为顶点法向,即样点法向。在分析网格顶点一阶邻域面几何特性的基础上,提出一种一阶邻域形心权重,使样点法向计算更为稳定与精确。网格曲面上的顶点法向计算公式可表示为
(1)
式中:m为顶点一阶邻域面的数量;ck为邻域面fk的权重值;nfk表示邻域面fk的法向,可表示为
k=1,2,…,m;vm+1=v1
(2)
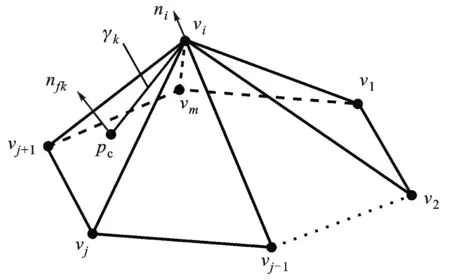
图2 网格顶点的一阶邻域
在三角网格曲面中三角面片以形状为等边三角形为质量最优,在同等条件下,三角面片形状越规整,它对顶点法向的贡献越大。为对三角面片形状规整程度进行量化,以三角形外接圆圆心与内切圆圆心的欧氏距离与外接圆半径的比值作为形状评价因子
(3)
式中:Ro、ro分别为三角形的外接圆圆心和内切圆圆心;R为外接圆半径。在[0,1]区间内,随着λ的增大,表示三角面片形状规整程度越高。当λ等于0时,三角面片的形状为退化三角形,即三点共线,可认为该面片对顶点法向没有影响;λ等于1时,三角面片形状等边三角形,此时三角面片规整度最高。
在一阶邻域面形状评价因子相同的条件下,邻域面的尺寸也对顶点法向有一定的影响,尺寸越小的邻域面几何性质与顶点处相似性越高,其法向对顶点法向的贡献越大。因质心可以很好地反映三角面片尺寸和形状,所以以邻域面的质心到顶点的距离来刻画邻域面尺寸这一影响因素,记为
γ=d(pc,vi)
(4)
式中:d(·)表示两点之间的欧氏距离;pc表示邻域面fk的质心;vi表示三角网格顶点。
由形状和尺寸可确定一个邻域面,故顶点一阶邻域面fk权重值可表示为
式中:λk为fk的形状评价因子;γk为顶点vi到fk质心的距离。故样点法向即顶点法向可表示为
(5)
基于网格顶点一阶邻域面形心权重的样点法向计算方法考虑了邻域面的形状和尺寸对顶点局部几何性质的综合影响,所得法向更为精确。
3 样点曲率稳健估计
曲率估计过程包含初步计算和加权修正两个阶段。在获得局部Delaunay网格曲面后,基于网格中样点一阶邻域面估计样点曲率,通过加权计算对其修正,提高样点曲率估计的稳健性。
对于局部网格中样点pi,其平均曲率和高斯曲率的估计公式[8]分别为
(6)
(7)
式中:αij、βij分别为连接样点pi和pj的对角;vij为pi指向pj的向量;N(i)为样点pi的一阶邻域点集;npi为顶点pi的法向,按式(5)计算所得;θj表示邻域三角形中以为顶点的角度值;Amax为网格曲面中pi所在Voronoi单元面积;∂M表示局部网格边界样点集合。局部网格中样点曲率估计示意图如图3所示。
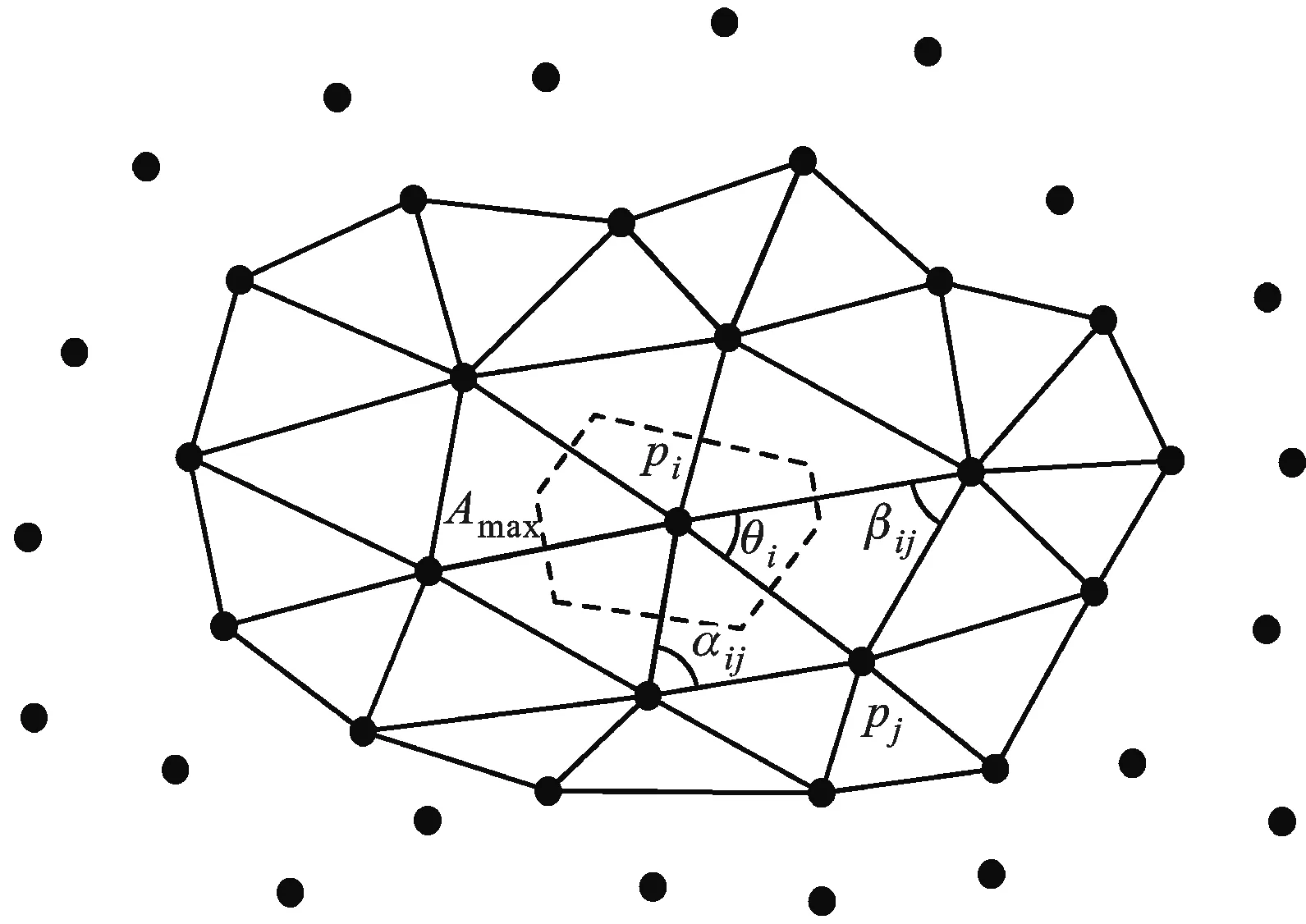
图3 局部网格中样点曲率估计示意图
获取样点曲率估计结果后,计算局部网格曲面中邻域点与目标样点间测地距离,基于所得测地距离确定不同邻域点权重系数,对目标样点曲率进行加权修正,最终实现样点曲率的平滑过渡。对于目标样点p,其平均曲率修正结果可表示为
(8)
式中:di表示在局部网格所构成图结构中邻域样点pi至目标样点p的最短路径长度,可近似表示该两点间的测地距离;h为目标样点p至所有邻域样点中最短路径长度的最大值;G(x)为核函数,表达式为
(9)
在式(8)中,将kH(p)替换为kG(p),即可获得高斯曲率估计结果。
在局部重建过程中,为散乱点集建立合理的索引结构可显著提高局部样本获取效率。目前有多种用于提高目标样点k近邻查询效率的空间索引,如空间八叉树[12]、k-d树[13]、R树[14]以及R*树[15]等。鉴于k-d树优越的空间索引性能和便于实现的特点,本文将其作为散乱点云的空间索引,实现邻域点集的快速查找。
综上所述,对S中任一样点p,其曲率估计完整流程如下:
(1)基于k-d树索引查询p的邻域点集并进行局部重建,获得局部重建网格D(φ(p))。
(2)基于样点一阶邻域形心权重,按式(4)计算D(φ(p))中任一样点法向。
(3)基于式(5)与式(6)估计D(φ(p))中任一样点的曲率。
(4)采用Dijkstra算法[16]计算目标样点p至邻域点集中任一样点的近似测地距离,并利用式(7)求解p点曲率。
4 实验与分析
为验证本文所提算法的有效性,在硬件配置为HP xw8600 Workstation(2.5 GHz,4.0 GB内存),操作系统为GNU/Linux的测试环境中,分别利用文献[3]算法、文献[5]算法、文献[8]算法与本文算法对如图4所示的不同点云模型进行测试,测试结果如图5所示。

(a)安雅(点数为1.02×106) (b)弥勒佛(点数为1.49×106) (c)维纳斯(点数为2.50×106)

(d)风扇盘(点数为0.21×106) (e)引擎罩(点数为0.62×106) (f)龙(点数为0.00×106)
将不同算法所得高斯曲率进行归一化处理,采用颜色索引表示曲率变化,可得模型高斯曲率云彩图,如图5所示。对于图4e所示引擎罩模型,文献[8]算法曲率估计结果与其他3种算法计算相比存在一定误差,这是因为文献[8]算法易受采样误差的影响,而其他3种算法对采样误差均具有一定的抑制作用。通过对比可知,本文算法与文献[5]算法所得曲率过渡较为光滑,尤其在曲率变化较大特征处,本文算法所得曲率过渡最为光滑。

图5 引擎罩点云数据不同算法高斯曲率估计结果
平均曲率是模型的重要几何信息,可作为型面特征度量标准应用于点云简化过程。为验证4种算法对平均曲率估计的准确性,以不同算法所得平均曲率为输入数据,对图4d所示的非均匀采样的风扇盘模型点云数据进行简化。简化后点云数据规模为原始数据的30%。图6a所示为基于文献[3]算法所得曲率的精简结果,精简后的点云分布较为均匀,特别在尖锐特征区域,未能保留足够多的点云数据。如图6b所示,基于文献[8]算法所得曲率进行精简的结果在尖锐特征处样点数据较基于文献[3]算法的精简结果有所增加。如图6c和图6d所示,文献[5]算法和本文算法精简所得点云数据在特征区域分布较为密集,并且通过对比可知,本文算法精简结果随曲率变化的趋势最为明显。
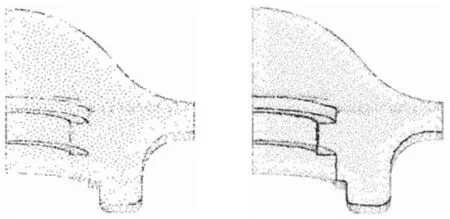
(a)文献[3]算法 (b)文献[8]算法

(c)文献[5]算法 (d)本文算法
为对本文算法曲率估计结果进行定量分析,构造半径为10 mm的球面的散乱点云数据(点数为104),以不同算法计算球面样点的高斯曲率和平均曲率。重复10次实验,分别统计各算法所得平均曲率高斯曲率与标准曲率的相对误差均值ηH、ηG和曲率标准差σH、σG。ηH、ηG可反映各算法曲率计算的精度,σH、σG可反映各算法曲率计算的稳健性,σH、σG值越小,表明曲率估计稳健性越好。如表1所示,文献[8]和文献[5]算法平均曲率计算精度最高,对于无采样偏差的点云数据,文献[5]算法采用的是文献[8]所提的Voronoi算法,因此,具有较高的计算精度,本文算法与文献[8]算法计算精度相当,高斯曲率计算精度高于其他算法且稳健性最好。
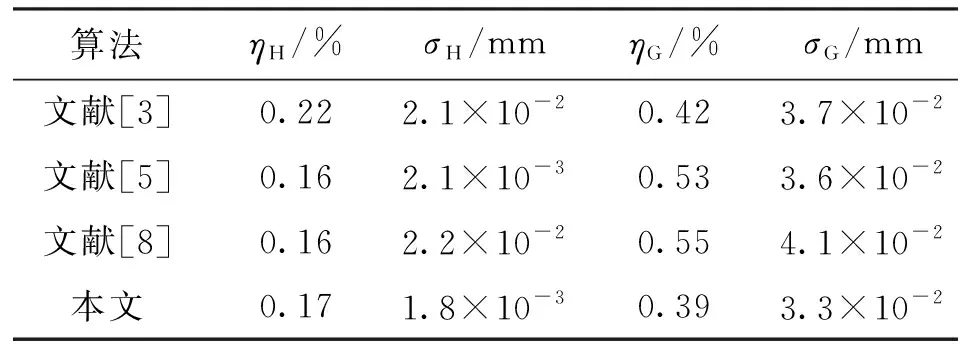
表1 不同算法所得球面样点曲率结果比较
为分析各算法对具有采样误差的点云数据的曲率估计效果,对球面点云数据添加均值为0、方差为0~1.0 mm的高斯噪声,分别统计各算法曲率计算结果的ηH、ηG和σH、σG,结果如图7所示。从图7中可以看出:随着噪声程度的增大,本文算法的曲率计算精度和稳健性均高于其他算法;相比于计算精度较高的Voronoi算法,本文算法在噪声为0时,计算精度与之相当,随着噪声程度的增大,本文算法优势明显,计算精度和稳健性可保持在Voronoi算法的1~2倍。
为验证本文算法的运行效率,分别采用文献[3]算法、文献[5]算法、文献[8]算法和本文算法对如图4所示的6组不同采样数据进行曲率估计,实验结果如图8所示。由图8可见,本文算法的运行效率低于基于样点一阶邻域面进行曲率估计的文献[8]算法,但明显高于基于局部拟合的文献[3]算法。文献[5]算法通过识别曲率估算异常区域并对其进行加权抛物面拟合估计离散曲率,其运行效率略低于本文算法。
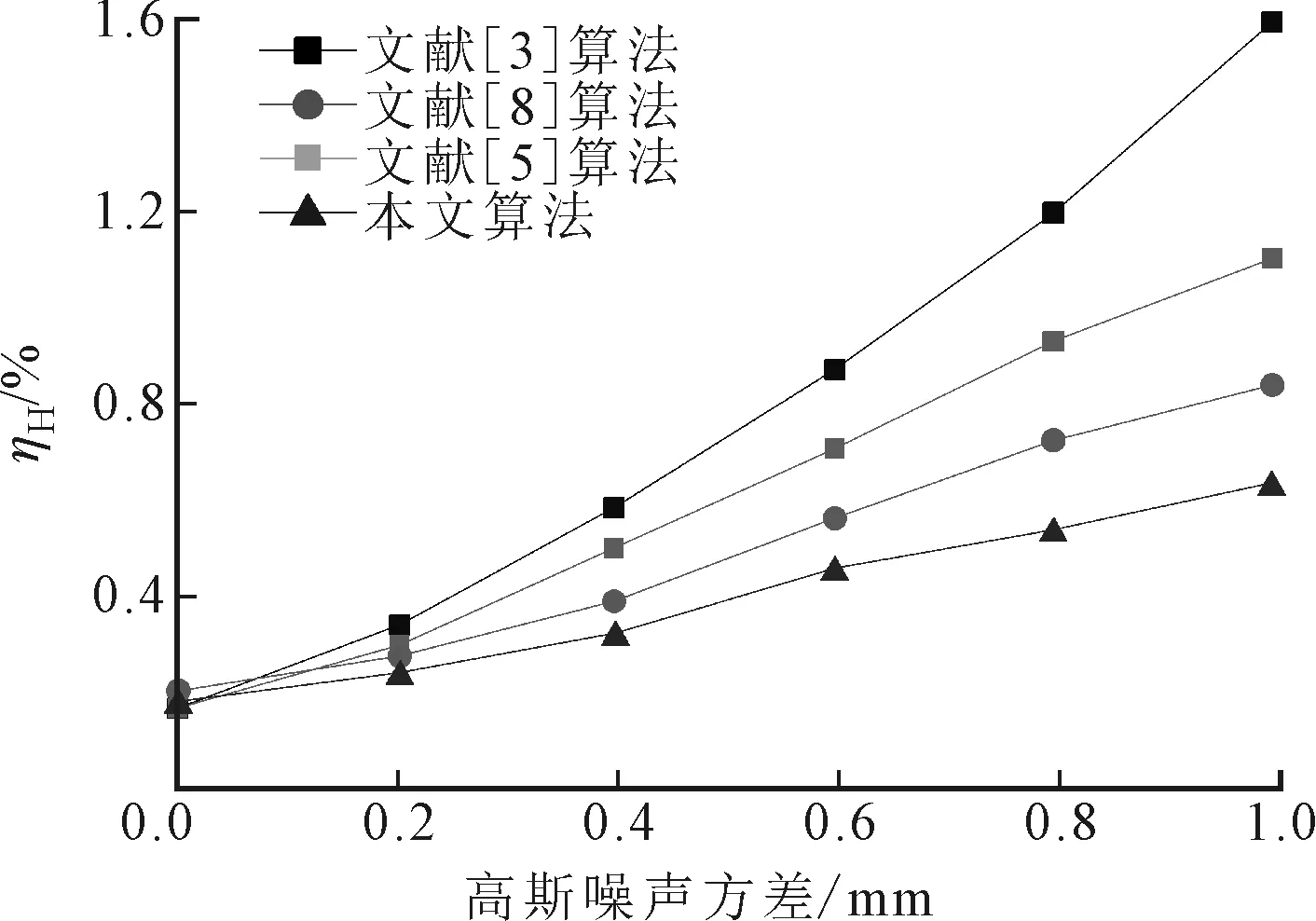
(a)4种算法的ηH比较

(b)4种算法的ηG比较
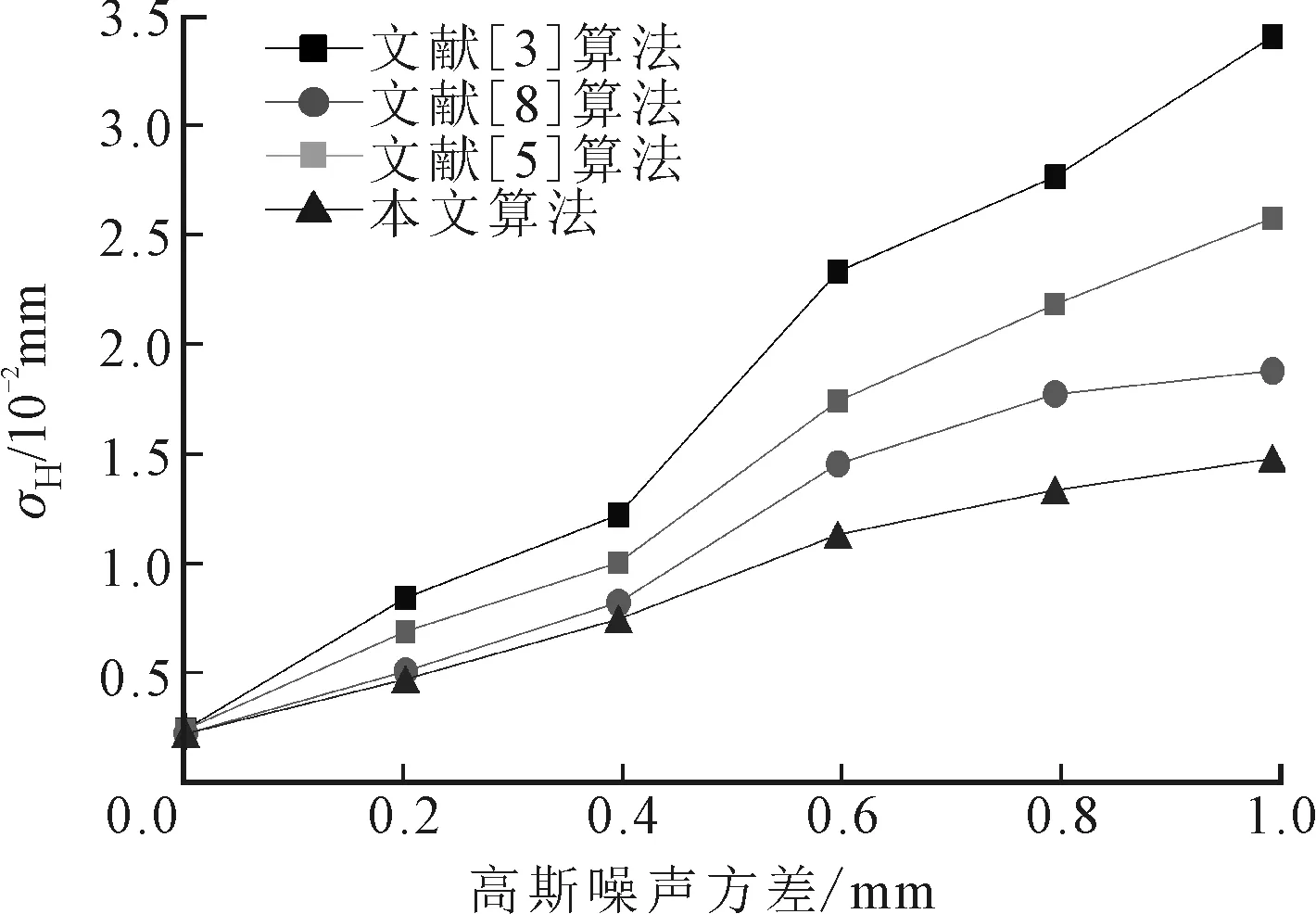
(c)4种算法的σH比较

(d)4种算法的σG比较
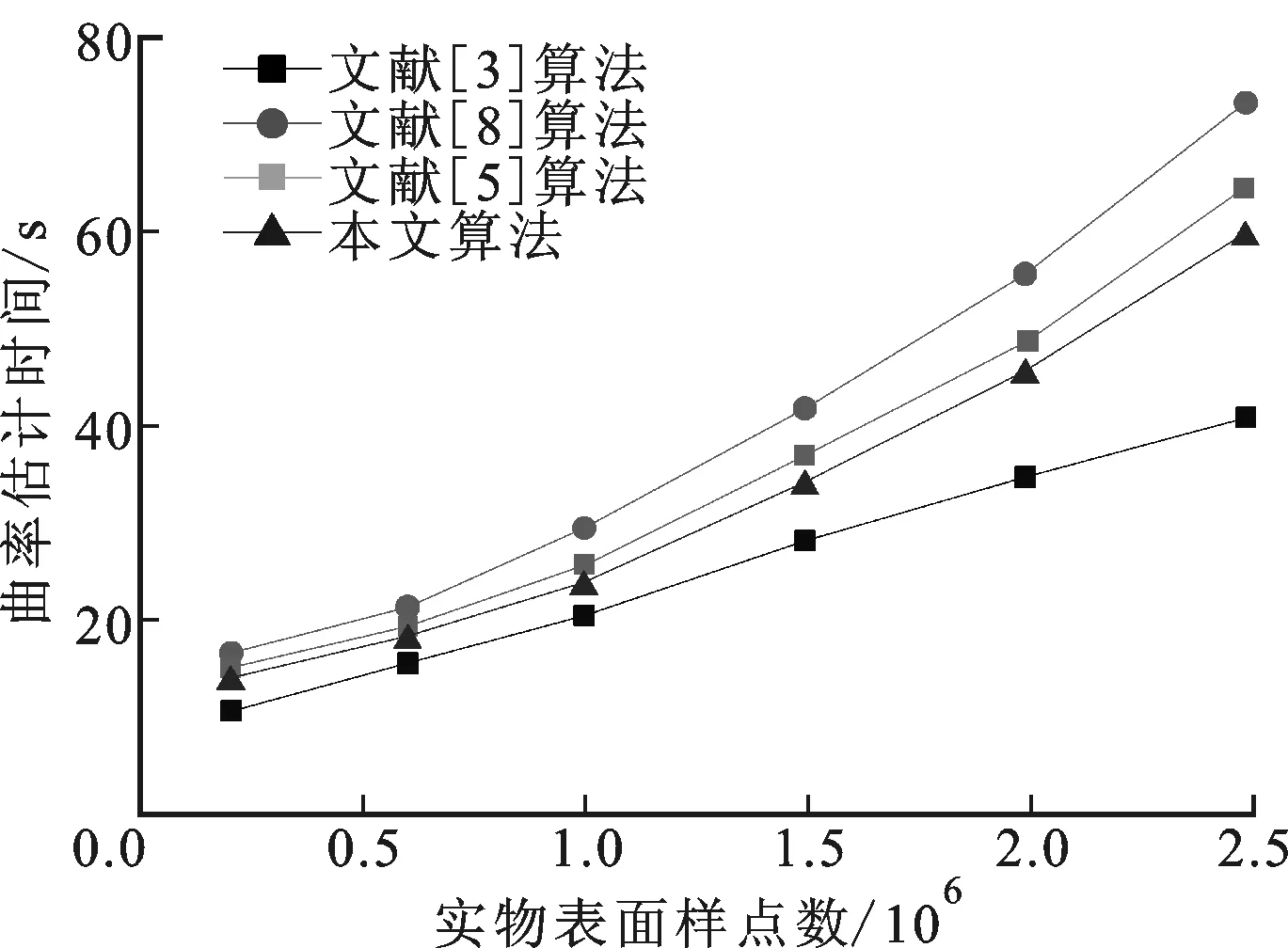
图8 不同算法曲率估计时间对比
本文算法所需主要参数有kη、kζ和θp。kη为局部样本的样点数量,其值大小决定着样点曲率估计质量。基于高斯核函数将局部样本中样点预估计曲率的加权和作为样点曲率的估计结果,kη值越大,参与加权计算的样点数量越大,样点曲率过渡越光滑,对于有噪声以及采样不均匀等缺陷的点云,其样点曲率计算越稳定,但过大的kη值会导致样点曲率过于平滑,且计算效率低下;kη值也不宜过小,kη值过小会导致曲面局部样本不够完备,无法准确反映曲面局部形状,导致样点曲率估计不准确,且无法稳健处理有缺陷点云的样点曲率估计问题。通过大量实验表明:对于采样均匀的点云,kη取15时可获得较为理想的实验效果。为更为稳健地处理非均匀采样点云的曲率估计问题,在以样点的15近邻点集为局部样本的基础上对其进行增益优化[17],获得可准确反映曲面局部形状的局部样本。kζ为添加辅助点后样点邻域点集样点数量,通过添加辅助点使得重建所得网格曲面中局部样本边缘样点可以有完整的一阶邻域面,辅助点的数量不宜过多,否则会导致局部重建效率低下。根据增益优化后局部样本样点数量N和样点局部采样密度确定kζ的取值,计算公式如下

(10)

5 结 论
通过对局部样本进行Delaunay网格剖分并滤除多余面片,可为样点构建邻域同构曲面,基于所得网格曲面并结合测地距离进行加权修正估计样点曲率,可得到如下结果:
(1)局部重建所得Delaunay网格曲面插值于采样点集,并且当采样密度符合要求时,拓扑同构于原表面,因此在复杂表面及尖锐特征区域均可实现理想的估计效果;
(2)通过对局部样本获取时所需参数kη、kζ合理取值,以一阶邻域形心权重计算样点法向进行曲率预估计,并基于测地距离对曲率估计结果进行平滑修正,能够有效抑制曲面采样误差对曲率估计结果的影响,提高了算法的稳健性;
(3)相比于Meyer提出的Voronoi算法,本文算法对采样精度较高的点云数据可保证与其相当的计算精度,对存在噪声的点云数据计算精度和稳健性均可提高1~2倍,基于k-d树构建空间索引获取局部样本并进行辅助点添加,使本文算法具有较高的计算效率,适用于大规模点云数据的处理。
